具有時滯和脈沖捕獲、污染物脈沖輸入的捕食-食餌-環境模型
章培軍, 王 震, 陳 恒
(西京學院理學院,西安 710123)
1 引言
害蟲爆發常常會引發嚴重的經濟和生態問題,我國作為一個農業大國,害蟲治理問題一直是關注的熱點,如何有效地控制害蟲也是大家最關心的問題.人們采取了各種措施控制害蟲的爆發,如化學控制(噴灑農藥)和生物控制(脈沖投放天敵)等,農業部門和研究學者們提出了害蟲綜合控制策略,要求合理有效地使用這兩種控制手段.
捕食-食餌模型是種群動力學中重要的模型,也是生態學與生物數學的一個重要研究課題,很多學者研究了影響捕食-食餌模型動態特性的因素,如功能反應、時滯、階段結構和收獲等,特別是這些因素的共同作用[1-4].然而,種群動力學中有許多自然現象和人為干預因素的作用都可以用脈沖微分方程來刻畫,脈沖效應在生態學系統中描述某些運動狀態的快速變化和跳躍,如生物種群個體的出生、人類對生物資源的脈沖捕獲與投放等[5-8],它能更真實地反映自然界的發展過程.
隨著工業、農業的快速發展,環境污染日益嚴重,研究環境中污染物或毒素對種群乃至生態系統的影響成為生態數學的熱點問題,早在20 世紀80 年代,Hallam 等[9-11]假設種群的增長率線性依賴于對毒素的吸收,研究了這種毒素排放到環境中對生物種群的影響,揭開了此方面的研究序幕.后來,很多學者在此領域進行了大量的工作,取得了很多研究成果[12-16].其中,李冬梅等[14]研究污染環境下脈沖輸入毒素對具有階段結構的單種群的影響,得到了種群滅絕和持久生存的充分條件,為控制環境中毒素對種群生長的影響提供了理論依據.然而,在實際生態系統中,幾乎沒有獨立的單種群存在,而是多種群共同存在,故考慮捕食-食餌關系的兩種群生態模型更符合實際.并且在污染的環境中,有些天敵受污染物或毒素的影響,使其數量減少,甚至滅絕,這使得我們需要控制污染物排放的數量和周期,保證天敵種群可以持續生存.另一方面,農藥噴灑過多,會使害蟲大量減少,但同時也對環境造成了嚴重的污染,在毒殺害蟲的同時,也殺害了天敵.為了保持生態平衡,不需要使害蟲完全滅絕,當害蟲不會帶來非常大的經濟損失時,我們希望害蟲和天敵能夠持續生存.
2 模型的建立及預備知識
綜上所述,本文研究脈沖污染的環境中,捕食者具有階段結構、食餌具有脈沖收獲的時滯捕食-食餌-環境模型的動力學性質,包括捕食者滅絕周期解的全局吸引性和系統持久性,考慮如下模型
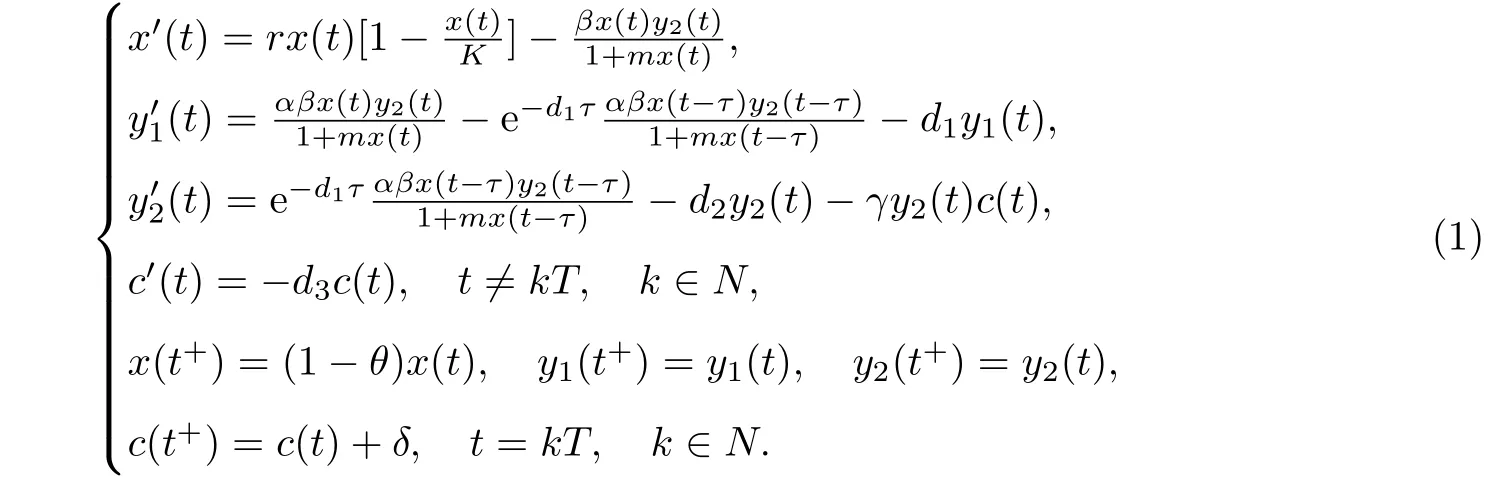
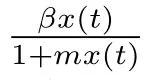
由于系統(1)的第一、三、四方程都不顯含y1(t),所以考慮系統
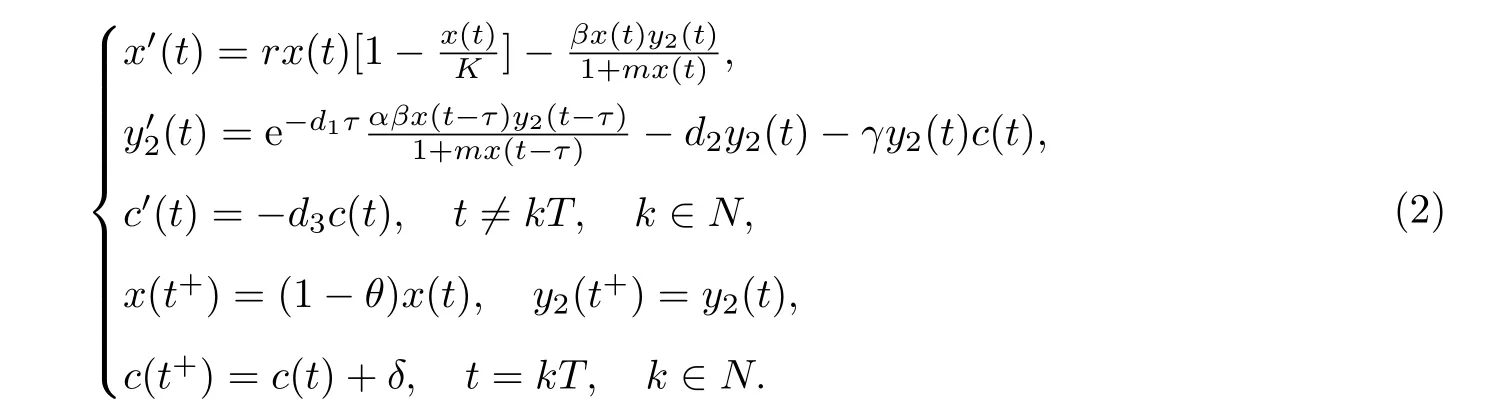
系統(2)的初始條件是
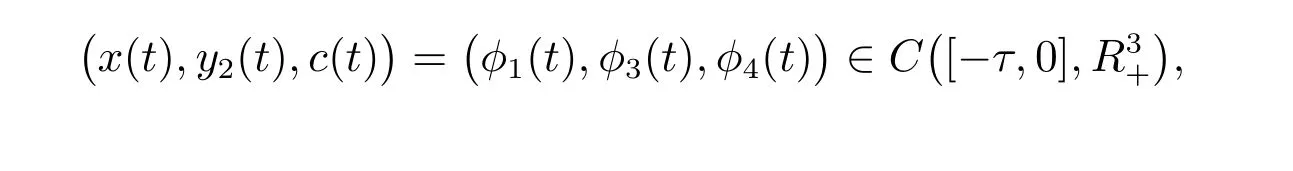
且在?kT(k ∈N)處不連續,而是左連續,即
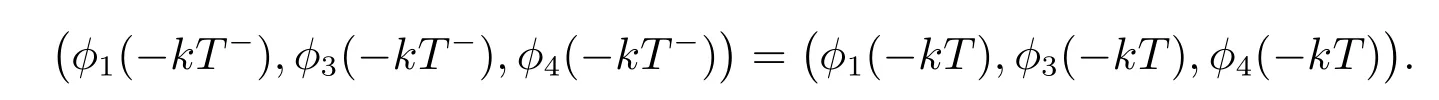
考慮到系統的生物意義,我們假設φ1(0)>0, φ3(0)>0, φ4(0)>0.
引理1[17]對于系統(1)的所有解,當t 足夠大時,存在一個常數Q>0,使得x(t)≤
Q, y1(t)≤Q, y2(t)≤Q, c(t)≤Q.
引理2[5]考慮脈沖系統
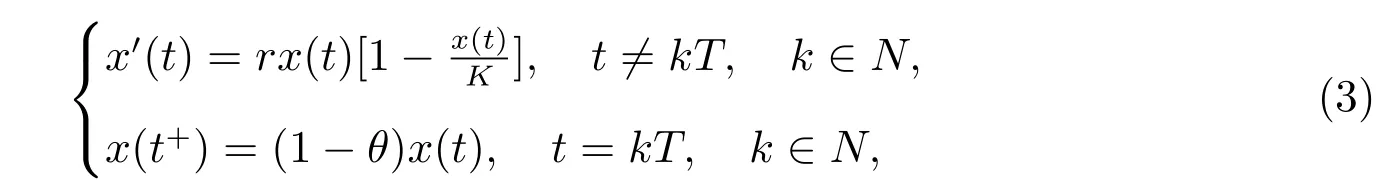
其中r >0, K >0, 0<θ <1,則系統(3)存在唯一正周期解
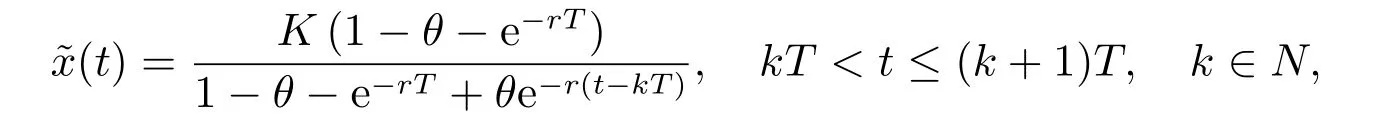
且全局漸近穩定.
引理3[15]考慮脈沖系統
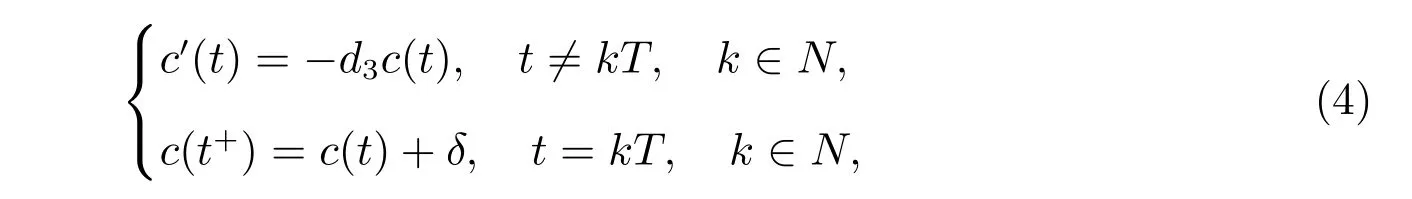
其中d3>0, δ >0,則系統(4)存在唯一正周期解
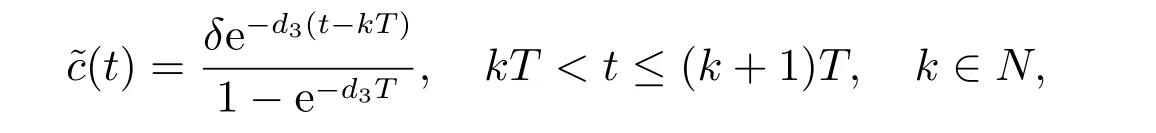
且全局漸近穩定.
引理4[18]考慮下列微分方程
x′(t)=ax(t ?τ)?bx(t),
其中a, b, τ >0,當?τ ≤t ≤0 時,x(t)>0,則:
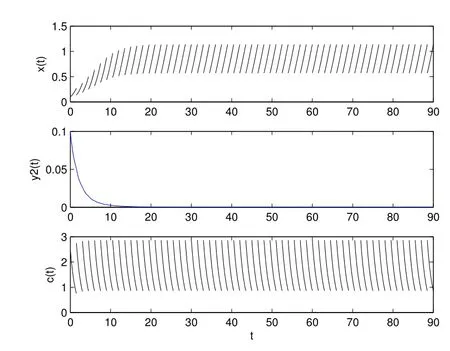
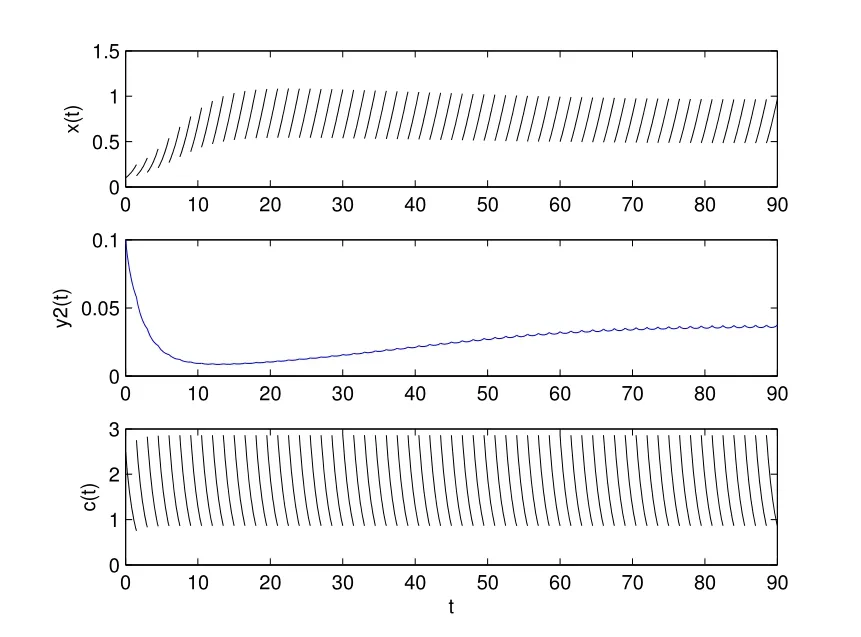
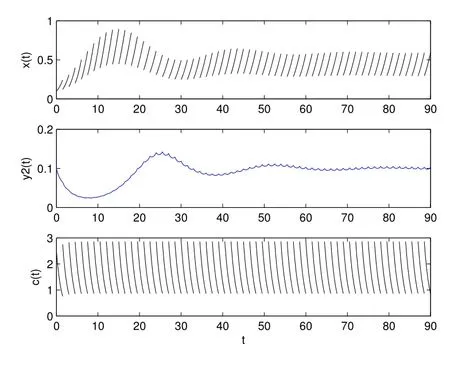
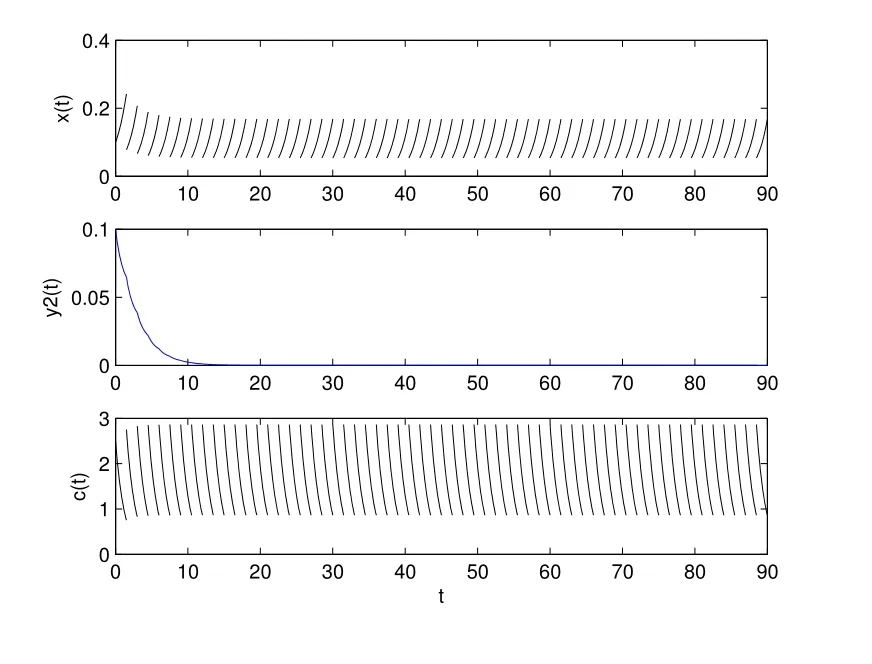
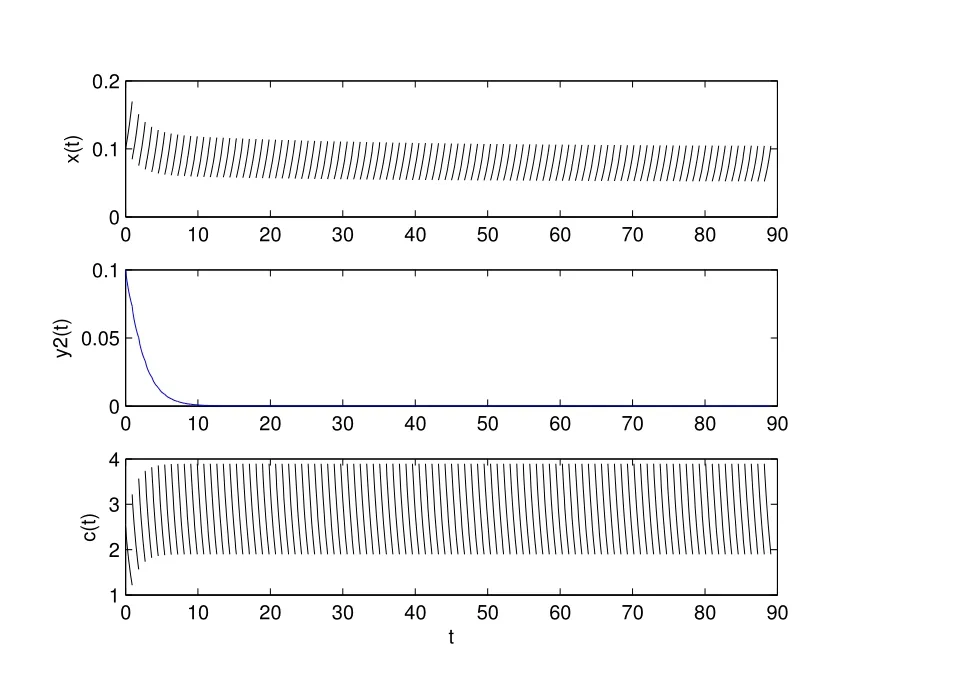
1) 如果a 2) 如果a>b,則limt→∞x(t)=∞. 在系統(2)中,令y2(t)=0, t ≥?τ,則可得到如下系統 由引理2、3,得到系統(5)的周期解為 且全局漸漸穩定. 定理1 如果R1< 1 時,則系統(2)的捕食者滅絕周期解((t),0,(t))是全局吸引的,其中 證明 由于R1<1,選擇充分小的ε0, ε1>0,使 從系統(2)的第一個方程,得到 考慮帶有脈沖的比較系統 由引理2,得到系統的周期解為 由比較原理[19],存在n1∈N 和任意小的整數ε0,對任意t>n1T,滿足 即 從系統(2)的第二個方程,得 考慮如下的比較系統 由引理4,得到limt→∞y(t)=0,因此,limt→∞y2(t)=0,對充分小的ε2> 0,存在整數n2>n1,任意t>n2T,有y2(t)<ε2. 對任意t>n2T,由系統(2)的第一個方程,得到 考慮帶有脈沖的比較系統 由引理2,得到系統的周期解 由比較原理,則存在整數n3>n2,使得對任意t>n3T,滿足 由于ε0與ε2充分小,得到 是全局吸引的,又由引理3 知,當t →∞時,c(t) →(t),從而系統(2)的捕食者滅絕周期解((t),0,(t))是全局吸引的. 推論1 如果θ =0 且τ >τ?1或δ >δ?,則系統(2)的捕食者滅絕周期解((t),0,(t))是全局吸引的,其中 推論2 如果δ =0 且τ >τ?2或θ >θ?,則系統(2)的捕食者滅絕周期解((t),0,(t))是全局吸引的,其中 定理2 如果R2> 1 且t 足夠大時,則存在正常數M,使得系統(2)的每一個正解(x(t),y2(t),c(t))都滿足y2(t)≥M,其中 證明 系統(2)的第二個方程,可寫成 定義 由系統(2),得到F(t)的導數 考慮帶有脈沖的比較系統 得到系統的周期解為 其中 根據脈沖微分方程的比較原理,則存在t1(t1> t0+ τ)和充分小的ε > 0,使得t>t1時,x(t)≥2(t)?ε,從而 由式(6)和(7)可知,對所有的t>t1,有 根據定理2 和以上討論,我們不難得出:當R2>1 時,系統(1)是持久的. 本文建立了一個在污染環境中,捕食者具有階段結構、食餌具有脈沖收獲的時滯捕食-食餌模型,并且污染物被脈沖地輸入到環境中,導致捕食者的數量減少.為了得到捕食者滅絕周期解的全局吸引性和系統持久性的充分條件,定義了兩個閾值R1和R2,當1 ?θ ?e?rT>0 時,明顯有R1>R2. 當R1< 1 時,由定理1 可知,系統的捕食者滅絕周期解是全局吸引的,捕食者在一段時間后滅亡,食餌種群及污染物的濃度呈周期波動. 當R2>1 時,由定理3 可知,系統是持久的,種群是持續生存的. 當R2< 1 < R1時,系統(2)的動力學性態會發生改變,例如,取r = 0.8, K =2, β =1, m=0.5, α=0.8, d1=0.3, d2=0.4, γ =0.1, d3=0.8, θ =0.5, δ =2, τ =0.5, T =1.5,經計算得到R1=1.0272, R2=0.4445,有R2<1 圖1 捕食者滅絕 圖2 系統是持續的 根據定理1 和3 可知,種群能否持續生存,主要依賴于食餌的捕獲率θ,污染物的脈沖輸入量δ 和脈沖作用的周期T.如果食餌的捕獲率θ、污染物的脈沖輸入量δ 過大,或者脈沖作用的周期T 過小,捕食者是滅絕的.選擇參數值r = 0.8, K = 2, β = 2, m =0.5, α=1.2, d1=0.3, d2=0.4, γ =0.1, d3=0.8, θ =0.5, δ =2, τ =0.5, T =1.5,經計算得到R2= 1.3335 > 1,由定理3 可知系統是持續生存的,如圖3 所示.在其它參數不變的情況下,當增加食餌的捕獲率至θ = 0.68 時,R1= 0.6592 < 1,由定理1 可知捕食者滅絕,如圖4 所示;當增加污染物的脈沖輸入量至δ = 30 時,R1= 0.8849 < 1,由定理1 可知捕食者也滅絕,如圖5 所示;當減少脈沖作用的周期至T = 0.9 時,R1=0.3439 < 1,由定理1 可知捕食者還是滅絕的,如圖6 所示.為了保持系統的持續生存,我們應該控制污染物輸入的周期和數量,同樣也要合理控制食餌的捕獲.這些為我們今后對生物資源的開發、種群數量的收獲及環境的控制提供了寶貴的理論依據. 圖3 系統是持續的 圖4 增加食餌的捕獲率至0.68 時,捕食者滅絕 圖6 減少脈沖作用的周期至0.9 時,捕食者滅絕3 捕食者滅絕周期解的全局吸引性
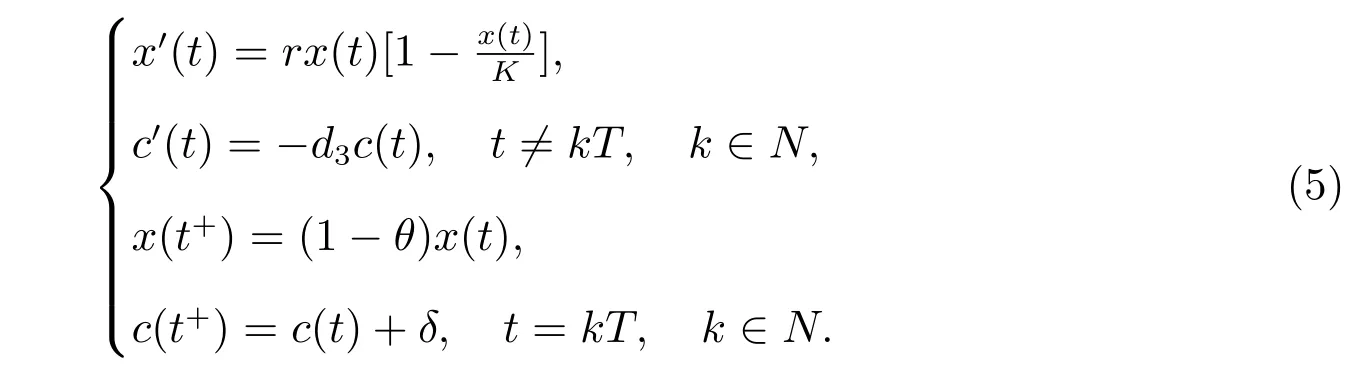
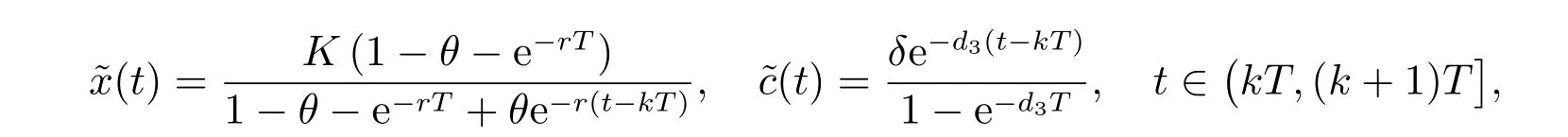
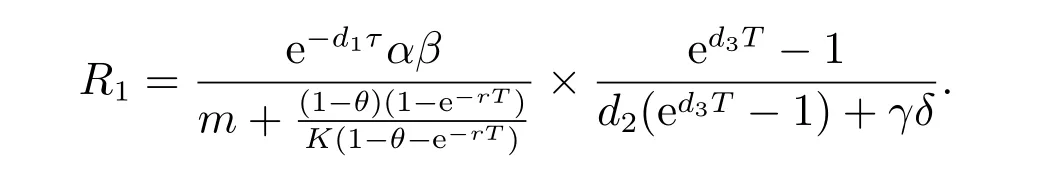
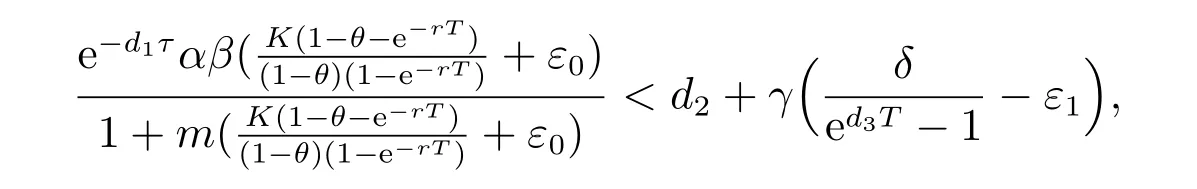
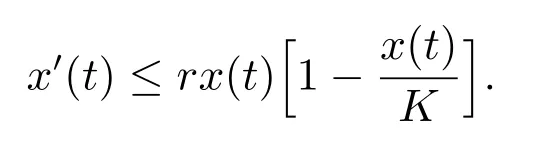
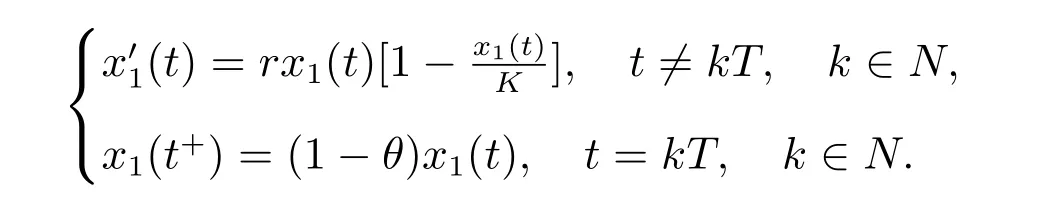
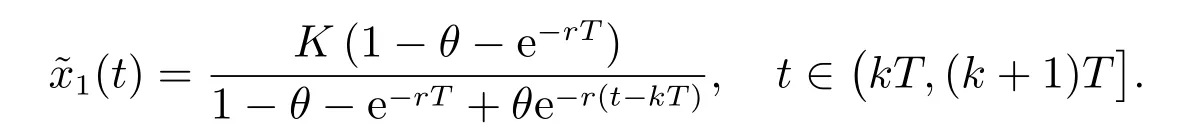
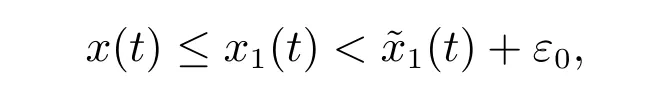
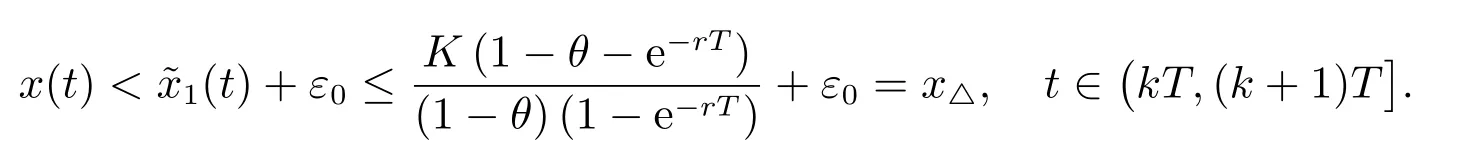
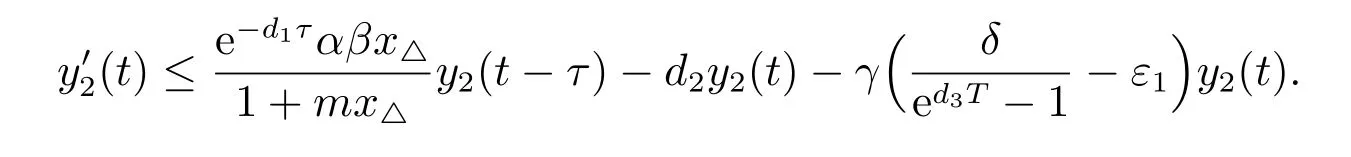
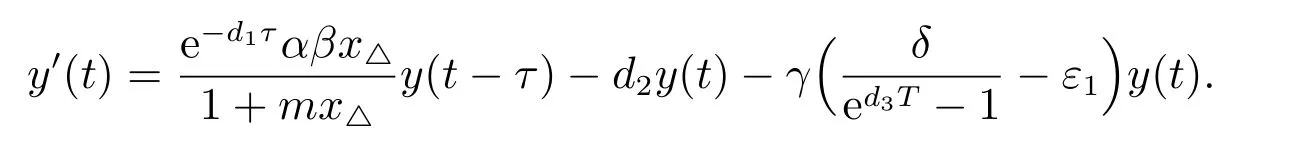
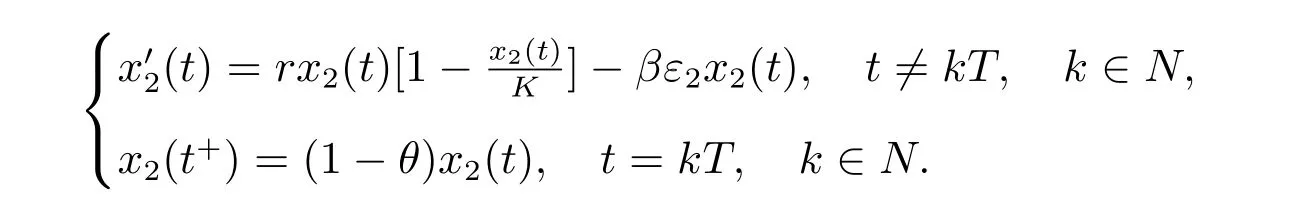
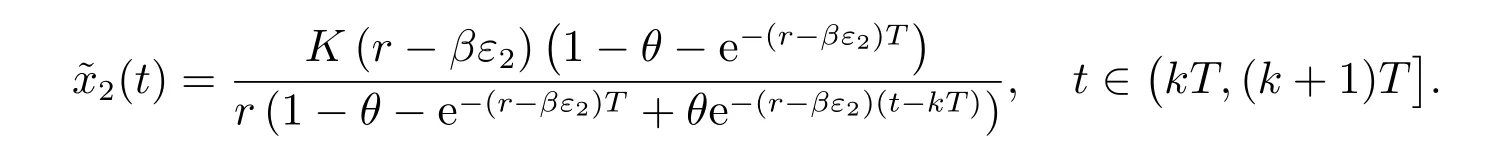
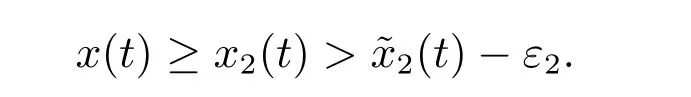
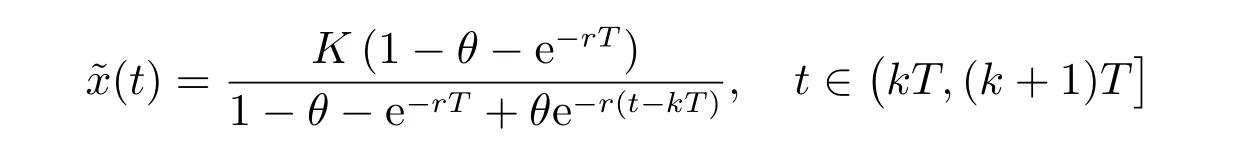
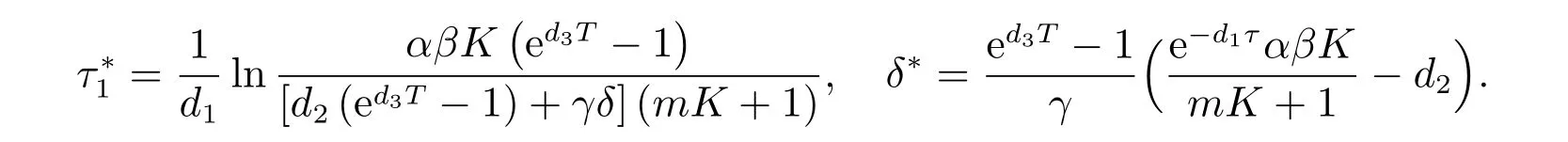
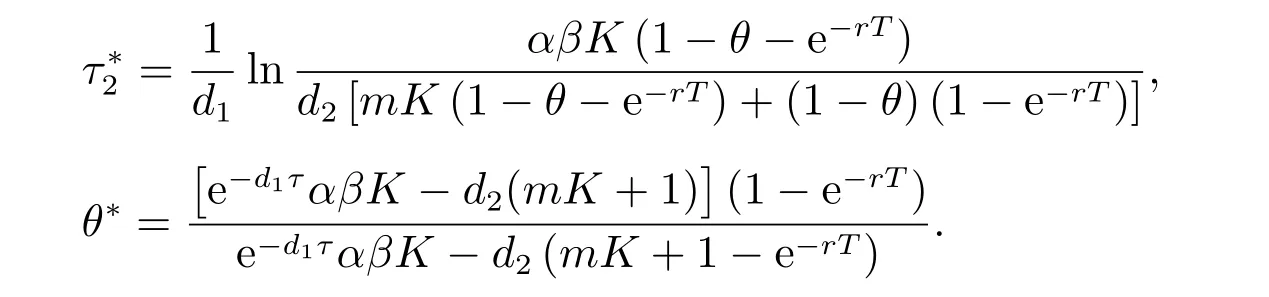
4 持久性
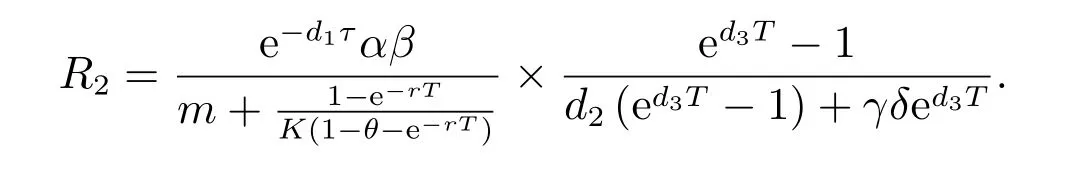
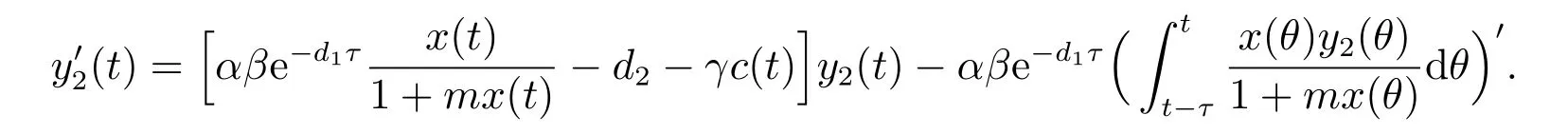
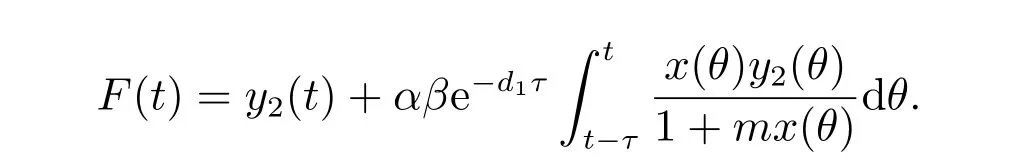
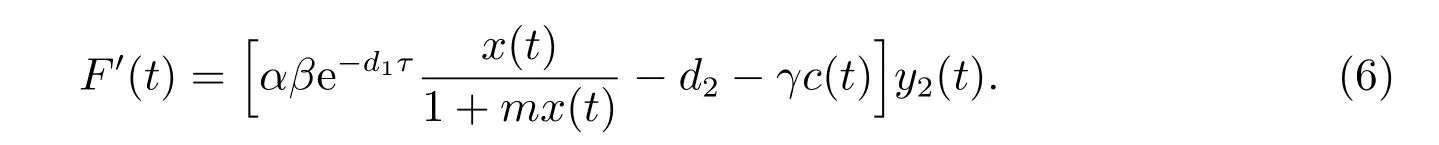

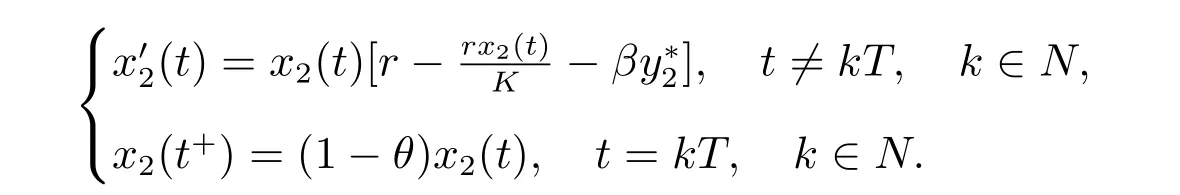
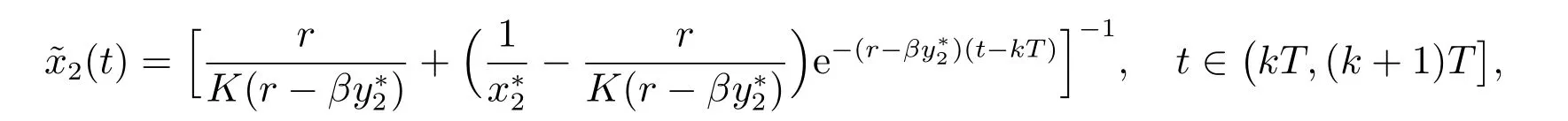
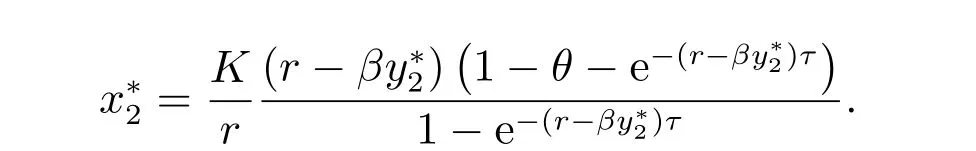

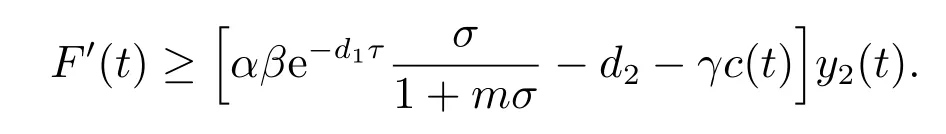


5 結論與數值仿真