關于易腐產品的M/M/1 生產服務庫存模型的最優控制

王 賽, 岳德權, 張媛媛, 田瑞玲

(燕山大學理學院，秦皇島 066004)

1 引言

隨著經濟的迅速發展，企業面臨的市場競爭越來越激烈，生產制造企業需要盡可能的降低庫存管理成本才能有可觀的經濟效益.對于生產制造企業來說，庫存不僅用來減少顧客需求，也可以用來調節生產，使得生產能夠平穩的進行.因此生產庫存模型及其庫存的控制管理一直是庫存理論的重要研究內容.

生產庫存策略是生產庫存系統的重要研究問題.施文武等[1]研究了一種多周期隨機需求的生產庫存控制系統，給出了費用函數，并設計算法求得最優控制策略.Benjaafar 等[2]研究了帶有不耐煩顧客的生產庫存系統，確定了最佳生產策略，分析了最優庫存控制策略對于各項性能指標的影響.Krishnamoorthy 和Viswanath[3]研究了具有(s,S)策略的帶有隨機服務時間的生產服務庫存系統，利用擬生滅過程方法得到了系統的穩態分布和費用函數.Baek 和Moon[4]研究了具有(s,S)策略的多個服務員的生產服務庫存系統，給出了系統的性能指標和費用函數，并通過數值例子確定了系統最優控制策略.Axs¨ater[5]研究了具有(s,S)策略且容量有限的生產庫存系統，假設系統生產時間服從伽馬分布，利用M/G/1 的相關理論，得到了最優的生產策略.Nair 和Jose[6]研究了具有(s,S)策略，兩種服務模式和重試需求的生產系統，求出了系統的性能指標，并建立了費用函數.

在上述關于生產庫存系統的研究中，都沒有考慮產品的易腐性.我國每年因為易腐性產品造成的損失之和高達千億[7]，所以易腐庫存系統的分析是很重要的.易腐性產品是指那些必須在有限時間內售出，否則將發生變質、損壞、揮發、過期且必須進行清倉處理的商品，如生鮮食品、水果、蔬菜、海鮮等.其顯著特點是在儲存和流通的過程中產品的數量會因腐爛變質、揮發、失效等逐漸減少.

易腐品的庫存問題已經引起了學者的廣泛關注.Kouki 等[8]研究了具有多種類型產品的易腐庫存問題，并且給出了系統的最優庫存控制策略.Sivakumar[9]研究了具有(s,S)策略，帶有有限個顧客的易腐品庫存系統，根據穩態方程求出了穩態概率向量，并建立了費用函數.Vijaya Laxmi 和Soujanya[10]分析了帶有服務中斷、重試需求和負顧客的易腐品庫存模型，并利用矩陣分析法求出了模型在穩態下的聯合概率分布，討論了系統的各項性能指標，確定了費用函數并得到了庫存的最優控制方案.Shophia Lawrence 等[11]研究了顧客有限的易腐產品的庫存系統.假設服務時間服從位相分布，產品壽命服從指數分布，利用拉普拉斯變換方法推導出了系統的性能指標，構建了費用函數.Manuel 等[12]研究了具有(s,S)策略的兩類客戶的易腐產品庫存系統，求得了穩態概率向量，并給出了費用函數的表達式.

在上述關于易腐產品的庫存控制文獻中，都是關注庫存系統的性能分析和庫存策略問題.目前在生產服務庫存系統中，關于易腐產品的生產庫存策略的研究工作較少.Sangeetha 等[13]研究了帶有重試需求的易腐品生產庫存系統.假設系統的顧客數量有限，基于(s,S)策略建立半馬爾可夫過程，利用線性規劃方法求出系統的最優生產速率，并給出數值例子進行分析.本文討論了易腐產品的M/M/1 生產服務庫存模型.假設顧客數量是無限的，規定當系統庫存為零時，允許顧客進入系統.根據擬生滅過程理論，我們求得了系統的平衡條件，進一步得到了穩態概率向量矩陣幾何解，性能指標及成本函數.最后給出數值例子，利用遺傳算法實現最優解的有效搜索，得到了系統的最優控制策略.

2 模型描述

我們考慮具有(s,S)生產策略的易腐產品的馬爾可夫生產服務庫存模型，可描述為：

顧客需求的到達服從參數為λ 的泊松過程，顧客到達系統后形成一個隊列，每位顧客的庫存需求量為一個單位庫存.系統中只有一個服務員，服務過程需要一定的時間，系統服務時間服從參數為μ的指數分布，服務規則為FCFS.

系統采用(s,S)生產策略，即當系統的庫存水平下降到s 時，生產系統立即啟動，并且每次只生產一個，直至庫存水平達到最大值S 時，才停止生產，其中s < S.生產時間服從參數為η 的指數分布.

產品壽命服從參數為γ 的指數分布，變質后的產品將不再具有價值.系統是無損失的，即當系統庫存為零時，顧客可以進入系統等待.假設需求到達過程，服務過程和生產過程是相互獨立的.

3 系統平衡條件

3.1 狀態過程

定義系統的狀態過程為ψ = {(N(t),I(t),C(t)); t ≥0}，其中N(t)表示時刻t 系統中的顧客數，I(t)表示時刻t 系統的庫存水平，C(t)表示時刻t 系統的生產狀態，其中C(t) = 0 表示生產系統關閉，C(t) = 1 表示生產系統開啟.根據(s,S)策略，C(t)應滿足如下關系

過程ψ ={(N(t),I(t),C(t)); t ≥0}的狀態空間為

將狀態按字典序排列可得過程ψ ={(N(t),I(t),C(t)); t ≥0}的無窮小生成元如下

其中

其中

D1是(2S ?s)×S 維矩陣，D2是(2S ?s)×(S ?s)維矩陣，C 是(2S ?s)×(2S ?s)維矩陣，I 是(2S ?s)維單位陣，I1是(2S ?s ?1)維單位陣.

3.2 系統平衡條件

由矩陣Q 的結構可知過程ψ = {(N(t),I(t),C(t)); t ≥0}是擬生滅過程[14].令H =C+B+A，則有

H =(H1H2),

其中

L1(i)=?(η+μ+iγ), 1 ≤i ≤S ?1,

L2(i)=?(μ+iγ), s+1 ≤i ≤S, G(i)=iγ+μ, 1 ≤i ≤S,

H1是(2S ?s)×S 維矩陣，H2是(2S ?s)×(S ?s)維矩陣.

定義H 的平穩概率向量為

π =(π(0,1),π(1,1),··· ,π(S ?1,1),π(s+1,0),π(s+2,0),··· ,π(S,0)),

平穩概率向量π 滿足如下條件

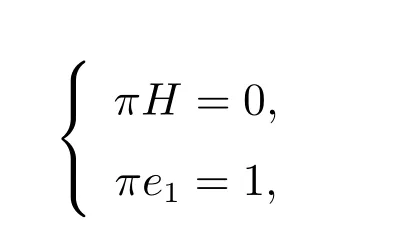
其中e1是所有元素為1 的(2S ?s)維列向量.通過計算整理，概率向量π 的各個分量可表示為

其中

由文獻[14]知，過程ψ ={(N(t),I(t),C(t)); t ≥0}正常返的充分必要條件為πAe1<πCe1.經計算整理可得

通過計算，πAe1<πCe1等價于

所以，公式(1)就是系統穩態平衡的充分必要條件.

注1 根據給出的πAe1和πCe1的表達式，可以看出πAe1表示系統的到達率，πCe1表示當庫存非零時系統的服務率，即系統的有效服務率.根據排隊論的知識，當系統的到達率λ 小于系統的有效服務率時，系統達到平衡狀態.

4 矩陣幾何解

本節利用擬生滅過程理論，首先給出系統的穩態概率分布的矩陣幾何解，然后討論率陣R 和邊界狀態概率的計算問題.定義穩態概率為

在穩態條件ρ < 1 下，Q 的平穩概率向量P 存在.相應于Q 的分塊結構，穩態概率向量P 分塊如下

P =(P0,P1,··· ,Pi,···),

其中

Pi={P(i,0,1),P(i,1,1),··· ,P(i,S ?1,1),P(i,s+1,0),··· ,P(i,S,0)}, i ≥0.

穩態向量P 滿足如下平衡方程

其中e 是元素都為1 的適當維數的列向量.根據公式(2)，我們可以得到如下方程組

由文獻[15]知，系統的穩態概率向量有矩陣幾何解

其中R 是矩陣二次方程

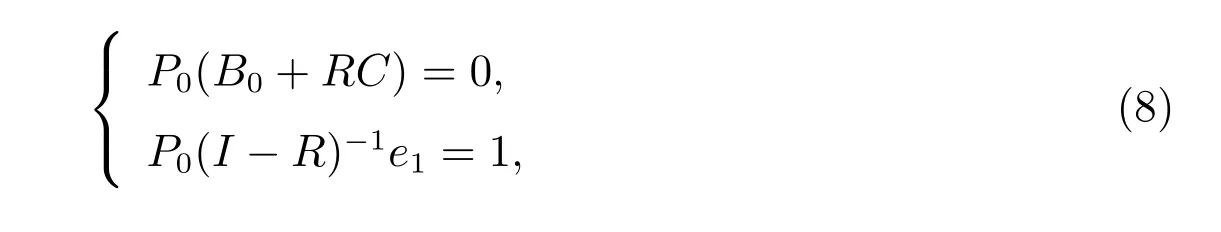
的最小非負解，其譜半徑sp(R)<1.P0是方程組的唯一正解，其中0 矩陣是元素都是0 的(2S ?s)維行向量，I 是(2S ?s)維單位矩陣.

為了計算系統的平穩向量，我們需要求出方程(7)的最小非負解R.在計算R 時，我們采用改進的循環簡約算法.循環簡約算法在文獻[16,17]中有詳細的介紹，循環簡約算法步驟如下：

步驟1 令

步驟2 矩陣^B(j)和率陣R 由以下循環迭代方法求得

直至迭代得到R 值的差的范數滿足‖R(j+1)?R(j)‖≤ε，從而求得率陣R；

步驟3 由方程(8)及Pi=P0Ri, i ≥0，即可求得平穩分布.

注2 為計算系統的平穩概率向量，我們需要求解矩陣二次方程(7)的最小非負解.在本文中，矩陣B、矩陣C 和矩陣A 均不是特殊矩陣，若直接利用方程(7)求解率陣R 則計算過程過于復雜，不易直接求出.例如，當采用(1,2)策略時，為求解R 需要求解一個九元二次方程組，求解過程相當復雜.因此我們使用上述算法，可近似求出率陣R 的數值計算結果.

例1 給定系統的參數值s = 1, S = 2, λ = 3.5, η = 5, γ = 0.05, μ = 8，根據率陣R 的計算方法，可近似求出R 如下

利用方程組(8)求解向量P0，結果如下

P0=(0.04132849666420,0.07048216383424,0.09789189421422),

再由公式(6)可以計算出系統的穩態概率向量.

5 穩態性能指標及成本分析

5.1 穩態指標

根據上述穩態概率向量的表達式，易得系統穩態性能指標，具體如下：

1) 平均隊長

其中δ1是元素為1 的(2S ?s)維列向量.

2) 平均等待隊長

3) 平均庫存

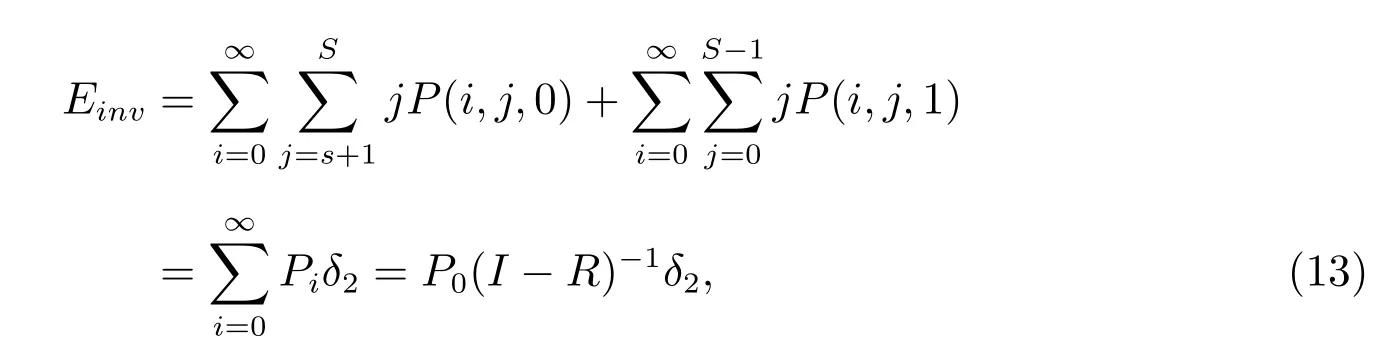
其中δ2為(2S ?s)維列向量，且δ2=(0,1,2,··· ,S ?1,s+1,s+2,··· ,S)T.

4) 平均易腐率

5) 平均生產率

其中δ3=(a b)T，a 是元素都為1 的S 維行向量，b 是元素都為0 的(S ?s)維行向量.

6) 平均生產啟動率

其中δ4為第(S+1)個元素為1，其余元素為0 的(2S ?s)維列向量.

5.2 成本函數分析

假設該庫存系統的成本主要由庫存保管成本、生產成本、設備啟動所需要的固定成本、產品腐爛的損失成本以及系統中每個顧客的等待成本組成.令單位時間單位庫存的保管成本為Cinv，單位時間的生產成本為Crp，每單位產品腐爛的成本損失為Cp，系統中每個顧客的等待成本Clq，每次重啟設備所需要的固定成本為K，則系統的成本函數C(s,S)為

顯然，系統的成本函數是關于庫存控制決策變量s, S 的非線性函數，且決策變量是離散的整數型變量.因為成本函數的表達式具有高復雜性，所以對于最小值的計算有一定難度.對于具體的數值例子，本文采用遺傳算法求解最優值.

5.3 遺傳算法

遺傳算法(GA)是模擬自然界遺傳、變異、適者生存的進化思想來求解優化問題，對目標函數和約束條件的要求較低.對于存在有限的可行解空間的純整數規劃問題，可采用適當的遺傳算法得到最優解，本文采用了豐建榮等[18]提出的利用二進制編碼的遺傳算法，具體步驟如下：

步驟1 隨機產生初始種群，個體數目一定.如果個體無效，那么重新隨機生成初始個體，直至有效；

步驟2 評價群體的適應度，找到最好的染色體；

步驟3 用輪盤賭策略對每一代種群中的染色體進行選擇；

步驟4 進行個體交叉操作，判斷個體的有效性.如果是無效個體，則隨機生成一個交叉位置進行交叉，直至有效；

步驟5 進行個體變異操作.如果產生無效個體，則重新進行變異操作，直至有效個體產生；

步驟6 由選擇、交叉和變異產生新一代種群；

步驟7 對新種群適應度評價，找到最好的染色體，將它與上一次進化中最好的染色體比較，記錄每一代進化中最好的適應度和平均適應度；

步驟8 如果不滿足算法終止的條件，轉到步驟3.否則，輸出當前最優個體，算法結束.

6 數值分析

本節通過數值例子來考察系統參數的敏感性.根據上一節設置的遺傳算法，設置種群大小為50，交叉率為0.6，變異率為0.01，算法終止條件為100 次(通過反復實驗，程序迭代100 次結束，穩定收斂到最優解)，并用Matlab R2014a 編程進行數值實驗.

表1 給出了參數λ 取不同的值時，系統的最優控制策略和一些性能指標的取值變化，其中參數設置為η = 5, γ = 0.05, μ = 8, Cinv= 10, Crp= 20, Cp= 50, Clq=200, K =2500.

表1 參數λ 的敏感性分析

由表1 可見，隨著參數λ 的增大，系統的安全庫存水平和最大庫存水平都呈上升趨勢.系統的平均庫存、平均易腐率、平均生產速率、平均等待隊長逐漸增加，平均生產啟動率逐漸減小，最終成本函數逐漸增加.對于企業來說，在系統成本參數確定的條件下，市場需求增加時，庫存控制的最優策略應相應的上調安全庫存水平和最大庫存水平.

表2 給出了參數η 取不同的值時，系統的最優控制策略和一些性能指標的取值變化，其中參數為λ=3.5, γ =0.05, μ=8, Cinv=10, Crp=20, Cp=50, Clq=200, K =2500.

表2 參數η 的敏感性分析

由表2 可見，隨著參數η 的增加，系統的安全庫存水平，最大庫存水平均呈下降趨勢.系統的平均庫存、平均生產率、平均易腐率先減后增，平均等待隊長逐漸減小，平均生產啟動率逐漸增大，最終導致系統的成本逐漸增大.對于企業來說，可以通過技術改進，更新設備等方法提高生產率.同時當生產效率提高時，庫存控制的最優策略需要下調安全庫存水平和最大庫存水平，企業在調整時還需要注意生產效率過高會造成產品堆積.

表3 給出了參數γ 取不同的值時，系統的最優控制策略和一些性能指標的取值變化，參數為λ=3.5, η =5, μ=8, Cinv=10, Crp=20, Cp=50, Clq=200, K =2500.

表3 參數γ 的敏感性分析

由表3 可見，隨著γ 的增加，系統最大庫存水平逐漸減少.系統的平均庫存、平均生產啟動率逐漸減少，平均生產率、產品的平均易腐率逐漸增加，平均等待隊長先增后減，最終導致系統費用增加.易腐產品的壽命參數γ 越小，產品的腐爛速度則越慢，系統成本越小.對于企業來說，可優化易腐品的保存方法，延長產品壽命，進而降低庫存成本.

表4 給出了參數μ取不同的值時，系統的最優控制策略和一些性能指標的取值變化，參數設置為λ=3.5, η =5, γ =0.05, Cinv=10, Crp=20, Cp=50, Clq=200, K =2500.

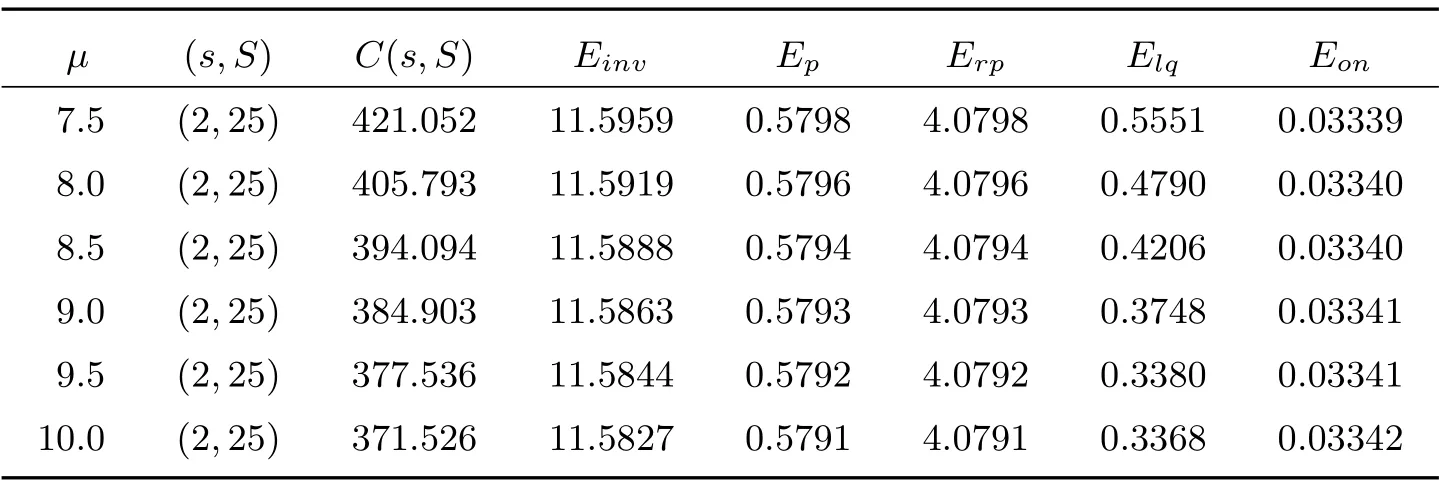
表4 參數μ的敏感性分析

由表4 可見，隨著參數μ的增加，系統的安全庫存和最大庫存水平保持穩定.系統平均生產啟動率逐漸增加，但增幅很小.平均生產率、平均庫存和平均易腐率、平均等待隊長逐漸減小，系統成本逐漸減小.在系統成本參數確定的條件下，服務速率越高，系統的成本則越低.所以對于企業而言，應該提高員工的服務效率，進而降低系統的庫存成本.

7 結論

本文研究了有關易腐產品的M/M/1 生產服務庫存模型，建立了關于系統中的顧客數、庫存水平和生產狀態三個隨機變量的三維擬生滅過程.利用擬生滅過程理論，求出了系統的穩態平衡條件，給出了系統的穩態概率的矩陣幾何解，并求出一些系統穩態下的性能指標.進一步構建了成本函數，針對系統成本函數的非線性、整數型變量的特點，運用遺傳算法，實現了最優解的有效搜索.通過數值實驗分析了系統參數的敏感性，這些分析結果，有助于生產型企業在外部參數發生變化時，根據實際情況及時調節庫存控制策略，對庫存管理實踐具有指導借鑒意義.