理論力學教具DIY系列(二)十字軸萬向節及轉角差異的演示模型

高云峰

(清華大學航天航空學院，北京100084)

十字軸萬向節是一種在工程中應用較為廣泛的傳動系統，它的主動軸與從動軸可以存在一定的夾角。十字軸萬向節具有制造簡單、可靠耐用等優勢，但存在主動軸與從動軸轉速不等的情況。在主動軸旋轉 360°的過程中，雖然從動軸也同樣旋轉 360°，但兩者的轉角、角速度并不總是相等，這就是十字軸萬向節的不等速性。

在理論力學的運動學教學中，十字軸萬向節是如何運動的，以及兩軸轉動的角度關系是一個難點。在實驗室中通常將兩軸轉動的差異用電信號進行轉換處理，學生感到不夠直觀。為了解決這一問題，本文首先設計制作出一個簡單的萬向節模型，然后導出萬向節的轉角差異關系，最后設計制作出了一個改進的萬向節模型，可以讓學生直觀地看出兩軸轉動角度的差異。

1 簡化版的萬向節設計及制作

十字軸萬向軸的要點是：主動軸與從動軸的夾角可以在一定范圍內變化，十字軸繞其中心點做定點運動。因此在設計時要考慮這兩個因素。

利用 AutoCAD軟件進行設計，利用激光切割機對密度板進行加工，可以很快獲得十字軸的零部件(圖1)。設計中考慮了接口的過盈配合，不需要膠水就可以把框架拼好(圖2)。

十字軸的連接軸也用密度板來實現，框架與連接軸之間留有微小縫隙，拼裝好后可以靈活轉動(圖3)。萬向節的底板分為兩大塊，兩者可相對做圓周運動且始終保持接觸，以方便圓弧邊緣有刻度顯示主動軸與從動軸的夾角；底板上可以插上立柱，而立柱可與十字軸連接(圖4)。

圖1 十字軸的零部件

圖2 軸的拼裝

圖3 十字軸的連接

用2根鐵軸分別連接十字軸兩端的邊框，并分別插到底板立柱的孔中，就做好了一個簡版的十字軸萬向節，它可以實現兩軸平行(圖5)以及兩軸有偏角(圖6)時的運動演示，很直觀。

圖4 可以改變角度的底座

圖5 兩軸平行情況

圖6 兩軸有偏角情況

激光切割的精度很高，誤差在0.1 mm以內，所以整個裝置拼好后，精度還是比較高的。當然以后如果可以用金屬來加工，誤差可以更小，摩擦也更小，演示效果也會更好。

2 萬向節的轉動角度關系

結合簡易版的萬向節模型，可以做運動分析，下面特別關注兩軸的轉角差異問題。

萬向節的運動坐標系如圖7所示，所有坐標原點均在O點，但為了方便觀看，圖中原點放在不同的位置。固定坐標系x0y0z0，初始時刻動坐標系x1y1z1與x0y0z0重合，且主動軸OM固連，OM軸沿x1方向，OA沿y1方向；動坐標系x2y2z2與從動軸ON固連，ON軸沿x2方向，OB沿z2方向；假設OMN始終在x0y0平面內，OM軸與ON軸的夾角為偏角α；OM軸轉動φ1后A到了A′，動坐標系變為x3y3z3；ON軸轉動φ2后B到B′，動坐標系變為x4y4z4。

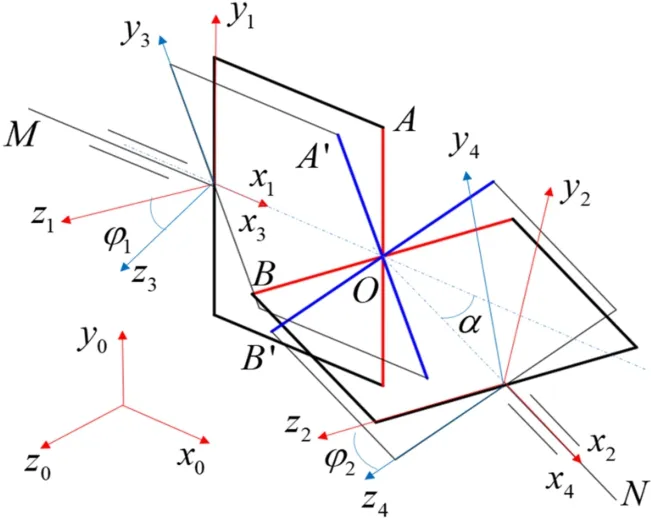
圖7 萬向節的運動分析

在這種假設條件下，A01是單位矩陣，其余各坐標系之間的方向余弦矩陣為

設rA′表示從O到A′的矢量，而表示rA′在坐標系xiyizi中的列陣，根據矢量的列陣在不同坐標系之間的轉換關系，則有

因為OA′垂直于OB′，有rA′·rB′=0，或，代入式(1)和式(2)后有

從而得到

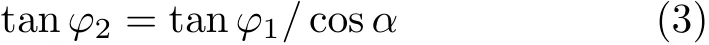
由此可見萬向節兩軸的轉動角度是不同的，設Δφ=φ2-φ1，式(3)可以變化為

圖 8顯示了不同偏角情況下兩軸轉角的差異。偏角α越大，兩軸轉角的差異就越大。

圖8 不同偏角時兩軸差異的關系

進一步對式(3)兩邊求導，可以得到

即兩軸角速度之比也隨時間周期性變化。

通常在理論力學求解萬向節角速度的習題中，會有意識地讓φ1=0或φ1=π/2，就是為了避免復雜的運動學分析，但這也容易讓學生誤解，以為兩軸角速度之比是常數。

3 改進版的萬向節的設計及制作

為了直觀看出萬向節兩軸轉角的差異，可以巧妙利用錐齒輪，把兩個非平行的轉軸變為兩個平行的轉軸，再類似鐘表的處理方式，把兩個平行軸變為共軸的“分針”和“秒針”轉動，這樣就可以通過“分針”和“秒針”的夾角，直接看出兩軸轉角的差異。

具體設計中的要點是：在裝置示意的俯視圖(圖 9)和正視圖 (圖 10)中，齒輪C通過錐齒輪與OM軸連接，然后與齒輪D1連接；齒輪E通過錐齒輪與ON軸連接，然后與齒輪D2連接。而齒輪D1和D2共軸且軸的延長線過O點。

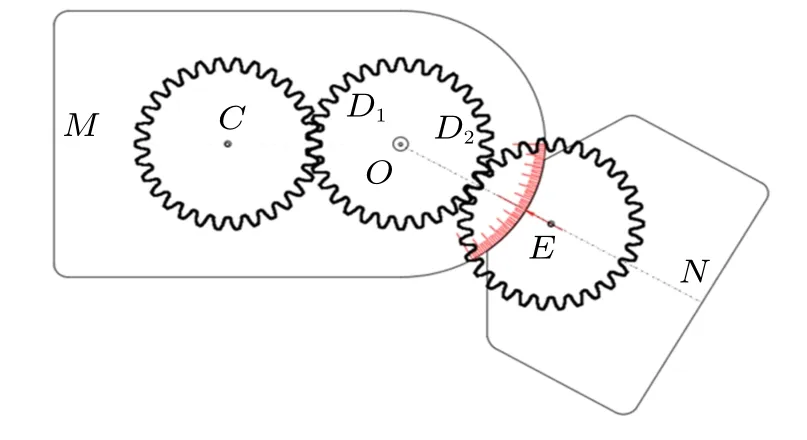
圖9 齒輪的位置安排(俯視圖)

圖10 齒輪連接關系(正視圖)

這樣的設計保證了當ON軸和OM軸保持不同的偏角α時，齒輪E總可以與齒輪D2嚙合。共軸設計將OM和ON的轉角同時在齒輪D1和D2中反映出來，再將指針分別與D1和D2齒輪固接，就可以通過看兩指針夾角的變化，直觀地看出萬向節兩軸轉角的差異。

圖11和圖12是改進后的裝置，其中C，D，E齒輪的齒數還可以適當改變，目的是將兩軸轉動的差異進行放大。

圖11 把水平軸變為豎直軸

圖12 變為共軸運動