虛物質導數與局部變分
——張量變分學的基本概念及其定義1)

殷雅俊

(清華大學航天航空學院工程力學系，北京100084)

本文標題涉及了三個關鍵詞：虛物質導數、局部變分、張量變分學，其中，虛物質導數和局部變分是似曾相識的詞匯：虛物質導數似乎只是在經典物質導數前面加了一個“虛”字；局部變分似乎只是在經典變分前面加了一個限定詞“局部”。

讀者也許會有疑問：“為何多此一舉？”“這不是玩弄詞藻嗎？”作者的辯解如下。引入虛物質導數和局部變分概念，是為了實現三個意圖：一是彌補張量分析學概念體系中破缺的對稱性；二是為張量變分學奠定基礎，三是為張量的協變變分學開辟道路。

限于篇幅，本文主要聚焦于前兩個意圖，即概念體系的對稱性和張量變分學。而張量協變變分學，則是后續文章綜述的重點。本文包括如下內容：(1)簡要回顧經典變分思想，評述其概念上的局限性；(2)拓展經典物質導數，引入虛物質導數概念；(3)依托虛物質導數，類比張量微分概念，定義張量局部變分概念，塑造張量變分與張量微分之間的對稱性；(4)類比張量微分學，展示張量變分學，揭示張量變分學與張量微分學之間的對稱性。

1 變分：一個“一句話說不清楚”的概念

大學時代，學習數學分析。課堂上，老師提出要求：“微分與積分的關系是什么？請用一句話說清楚。”作者小心翼翼地回答：“逆運算。”老師挑起大拇指：“高，實在是高！用一句話說清楚已經相當不易，你竟然用一個詞就說清楚了。”高興之余，老師進一步提高標準：“請用一個字說清楚！”受到老師的稱贊，信心大增，脫口回答：“逆！”

當年老師的苛刻要求，產生了持久的影響。從此，作者養成了思維習慣：對重要的概念，一定要理解到這樣的程度--用一句話說清楚其內涵和外延。

后來，學習力學中的變分原理。作者突然發現，如果問：“什么是微分？”一句話能說清楚。如果問：“什么是變分？”一句話竟然說不清楚了。

2008年，作者曾被前輩追問：“怎樣理解變分？”作者謹慎地“用一句話”答道：“對參變量的導數。”雖然用了“一句話”，但似乎并沒有“說清楚”。實際上，這個說法，對數學學者尚可接受，但對力學學者仍顯費解。

如果繼續追問：“什么東西對參變量的導數？”作者能給出的答案是“泛函對參變量的導數”。這個答案當然不算錯，但有局限性。

2 從歷史的天空看經典變分概念的整體性

歷史地看，變分似乎是個整體性概念。

整體和局部及其相互關系，是哲學家關注的問題，也是自然科學家感興趣的問題。

早年學習彈性力學，作者深受如下陳述的影響：彈性力學的基本問題有兩種提法，一是微分提法，二是變分提法。后來，作者自己成了教師和學者，對兩種提法有了更深刻的理解：微分提法體現了牛頓和萊布尼茲的局部化數理分析思想，而變分提法則體現了歐拉和拉格朗日的整體化數理分析思想。

由此，作者樹立起了牢固的觀念：微分是局部性概念，變分是整體性概念；

微分被定義在一個點的鄰域內，變分被定義在物質構型空間上；微分提法對應局部化數理分析之路，變分提法對應整體化數理分析之路。

從力學的角度看，上述觀念似乎經得起時間考驗。場函數的微分，涉及空間域上“點的鄰域”內場函數的增量。“點的鄰域”當然是局部性概念。彈性力學中的運動微分方程，建立在微單元體上。微單元體是“點的鄰域”的幾何化形態，自然是局部性概念。

泛函的變分，是定義在物質構型空間上的泛函的增量。彈性力學有最小勢能原理和最小余能原理。兩個原理分別涉及勢能泛函的變分和余能泛函的變分。勢能泛函和余能泛函都表現為物質構型空間上的積分。物質構型空間是整體性的概念，泛函自然也是整體性概念。

分析力學有最小作用量原理。克萊恩在他的名著《古今數學思想》中指出：“變分學的早期工作幾乎不能和微積分區分開來。但是，隨著變分法的深化，牛頓之后的偉大先驅們很快意識到：一個全新的、具有自己的特征問題和方法論的數學分支已經產生了。”“這個新學科，對于數學和科學來說，其重要性幾乎可以和微分方程相比，它為整個數學物理提供了一個最重要的原理。”這個“最重要的原理”，即最小作用量原理。

作用量一般表現為時間段上的積分。當說“作用量的變分”時，研究的是定義在時間段上的作用量的增量。時間段是整體性的概念，作用量當然也是整體性的概念。

很顯然，先驅們思考變分學的角度，著眼于整體。其中的核心概念，是泛函的變分或作用量的變分。

然而，這產生了誤導，使得作者產生了如下誤解：由于變分的作用對象都是整體性概念，故變分就是個整體性概念。教學過程中，作者有意無意地將這樣的觀念傳遞給了學生。

近年來，隨著研究的深入，作者意識到，上述觀念限定了教師和學生的想象力。實際上，如果研究對象不是泛函或作用量，而是張量場函數，那么，著眼點就不應該是整體，而應該是局部。

3 張量變分的局部性與概念體系對稱性的破缺

2002年，作者研究生物膜力學時，強烈地意識到，需要清晰地引入一個概念--曲率張量的變分。

生物膜是軟物質，可以將其抽象成柔性曲面。不難想象，柔性曲面幾何形狀的任何漲落，都會誘導曲率張量的擾動。那么，怎樣才能最有效地度量曲率張量的擾動量？

當時，作者借鑒彈性力學，用虛位移概念刻畫柔性曲面的漲落。于是，很自然地，就把曲率張量的擾動量視為“曲率張量的變分”。

如何快速計算曲率張量的變分？作者意識到，不同于曲率張量的微分，“曲率張量的變分”沒有現成的計算模式，故當時只能憑物理直覺“拼湊”出其計算式。

數學力學中的概念，一般都有兩個表達式，一個是定義式，另一個是計算式。其中，定義式在先，計算式在后，計算式源自定義式。“曲率張量的變分”作為一個基本概念，既沒有計算式，也沒有定義式。因為沒有定義式，當然也就無法“一句話說清楚”其內涵和外延。

“曲率張量的變分”，無定義，難計算。然而，“曲率張量的微分”，可定義，可計算。作者發現，類似的概念上的對稱性破缺，不是孤立的現象，竟然普遍存在于張量分析中：有一般意義上的“張量微分”概念，但沒有一般意義上的“張量變分”概念。

作者還發現，概念上的對稱性破缺帶來的直接后果，是理論上的對稱性破缺：張量微分學的大廈巍然挺立，但張量變分學的原野卻一片荒漠。這并不奇怪：基本概念是理論的基石。張量微分學的大廈奠定在張量微分概念的基礎之上。相反地，缺少了基礎性的張量變分概念，張量變分學的大廈就無從談起。

追根溯源，可以發現，對稱性破缺的根本原因，源自局部性概念與整體性概念之間的錯配：張量場函數可以是局部性概念，微分是局部性概念。這樣，“張量場函數/微分”就是兩個局部性概念的組合，渾然天成。然而，經典的變分“被認為”是整體性概念，“張量場函數/變分”，是局部性概念與整體性概念的疊加，難以匹配。

作者想起智者的忠告：紛繁之處，可嘗試分類；混淆之處，可嘗試定義。顯然，要糾正概念組合的錯配，最便捷的方法是塑造出一個局部性概念--張量場函數的“局部變分”。這樣，就相當于對籠統的變分概念進行了更精細的分類--整體性變分和局部性變分。當然，局部變分概念難以借助經驗提煉出來，只能借助理性塑造出來。

4 張量場函數的虛物質導數——局部變分概念的邏輯基礎

如何塑造張量場函數的局部變分概念？作者的作法是“先為局部變分概念尋找一個邏輯基礎”。2016年，找到了突破口：作者從“虛”字上獲得了靈感。

力學史上，從“實”到“虛”的觀念進化，對應著重要的思想飛躍。分析力學和彈性力學，都涉及一個十分基本的概念--虛位移。彈性力學中虛位移的定義很簡潔：就是運動許可位移。滿足運動許可的虛位移有無窮多，構成無窮集合。而真實位移只是虛位移的特例，只是無窮集合中的特殊元素。

分析力學中，“虛”字照樣引人注目。分析力學的理論體系，可以被奠定在不同的基本原理基礎之上：拉格朗日方程，被奠定在達朗貝爾原理的基礎之上；吉布斯阿佩爾方程和凱恩方程，被奠定在高斯原理的基礎之上。從達朗貝爾原理到拉格朗日方程，虛位移概念發揮了重要作用。同樣，從高斯原理到吉布斯阿佩爾方程和凱恩方程，虛加速度概念不可或缺。

在速度和加速度之間，還有一個運動學量--虛速度。虛速度，就是運動許可速度。歷史上，虛速度概念并沒有逃過先驅們銳利的眼睛。分析力學中，除了達朗貝爾原理和高斯原理，還有約旦原理。虛速度是約旦原理中決定性的概念。

注意到，位移，速度，加速度，不論“虛實”，都是定義在物質點上的概念。論及“物質點”，連續介質力學的一個概念進入了作者的視線--物質導數。

需要說明的是，幾何論中，確有“對參變量的導數”概念。如果“參變量”被取為時間變量，且“對參變量的導數”被定義在運動的物質點上，即可得到物質導數[1-2]。

在作者的印象里，物質導數是“實”的概念，用以刻畫物體“真實”的運動。后來，作者意識到，這只是先入為主的自我設限。實際上，沒有任何理由認為，也沒有任何權力規定，物質導數必須是“實”的。正如虛位移、虛速度和虛加速度，完全可以自由地引入“虛”物質導數概念。正如虛位移是運動許可位移，虛物質導數即為運動許可物質導數。

虛物質導數，可以視為實物質導數的推廣。反過來，實物質導數，可以視為虛物質導數的特例。

從虛物質導數概念出發，就可以定義局部變分概念。也就是說，虛物質導數，可以被選定為局部變分概念的邏輯基礎。

一旦涉及到物質導數，就得關注物質占據的空間及其運動的描述方式。

5 物質空間及其運動描述方式

為了簡化形式，采用平坦空間。至于運動的描述方式，最基本的有歐拉描述和拉格朗日描述[1]。本文采用拉格朗日描述，是為了簡化理論的解析結構。簡化到極致，讀者便可輕松地理解本質和思想。

平坦空間拉格朗日描述下，張量場函數T具有如下函數形態

T既是拉格朗日坐標xm的函數，也是時間參變量t的顯態函數。這里的時間t，是一般參變量的特殊情形。從數學的角度看，xm和t都是自變量，地位完全平等，沒有本質的差異。然而，如果從力學的角度看，xm被賦予了幾何意義和物理意義，t則被賦予了物理意義。此時，xm是自變量，t是參數。物理學和力學中，被xm刻畫的連續函數，大都是“場”函數。

嵌入在連續體上的拉格朗日坐標xm的集合構成了一個實數域，稱之為拉格朗日空間域。連續體的運動發生在某個時間段內。這個時間段也構成一個實數域，稱之為拉格朗日時間域。張量場函數T(xm，t)在空間域上的變化，引出經典微分，在時間域上的變化，引出局部變分。

拉格朗日描述下，時間t與坐標xm居于同等地位。時間域與空間域也居于同等地位。時間t的引入，可以從運動的角度看變分概念的本質。

注意到，作用量中包含了時間，故似乎是動態概念。而連續介質力學中的勢能泛函和余能泛函，似乎都是靜態的概念。也就是說，能量泛函中沒有引入時間。當然，“沒有引入時間”，不等于“沒有時間概念”。能量泛函的增量(或變化)是物體運動的結果，而運動總發生在某個時間段內。因此，能量泛函中本來就有時間。實際上，理解了本文之后，讀者就會意識到：一旦允許時間自變量出現在能量泛函中，能量原理就會容易理解得多。

為便于讀者理解，下面采用比較分析法，同時展示張量場函數在空間域上的經典微分和時間域上的局部變分。

6 張量場函數在空間域上的經典微分

研究拉格朗日空間域中的微分，只需保持拉格朗日時間參變量t不變。固定時間參變量t，相當于令時間“凝固”或“凍結”。此時，看到的是t時刻靜態的物質空間。令拉格朗日坐標xm產生一個增量Δxm，進而求張量場函數T的增量ΔT

由于拉格朗日坐標xm對應于物質點，因此，式(2)的含義是物質點(xm+Δxm)的張量值與物質點xm的張量值之差。

大戰在即，豆腐坊的生意卻比往日更繁忙。假如不是四周槍炮林立，不是當街口一堆堆疊得小山似的沙包，還有沙包后伸出來的輕重機槍，光看豆腐坊的生意還真和平日里沒啥兩樣：幾大口鐵鍋一溜排開，火頭正旺，入了鍋的豆腐水滋滋冒著泡；幾個伙計光著膀子，系著圍裙，正抬著一大桶豆腐水往木格子里倒，只消一會，點了鹵的豆腐就結得硬硬邦邦。

固定時刻t，在xm的鄰域內，將T(xm+Δxm，t)展開為泰勒級數

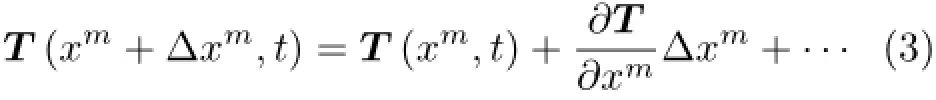
這里的泰勒級數，是場函數T(xm+Δxm，t)在拉格朗日空間域上的展開形式。于是式(2)重寫為

由式(4)右端的一階項，就可以定義出拉格朗日空間域上張量的微分dT

式(5)可以推廣到任意場函數。

經典偏導數?T/?xm和經典微分dT，是張量微分學的基礎性概念。這兩個概念定義之后，張量微分學的理論體系，就大體上確定了。

7 張量場函數在時間域上的局部變分

研究拉格朗日時間域中的變分，只需保持拉格朗日坐標xm不變，令拉格朗日時間t產生一個增量Δt，進而求張量場函數的增量ΔT

在t的鄰域內，將場函數T(xm，t+Δt)展開為泰勒級數

這里的泰勒級數，是場函數T(xm，t+Δt)在拉格朗日時間域上的展開形式。展開過程中，保持拉格朗日坐標xm不變，亦即緊盯運動的物質點不變。根據拉格朗日描述下物質導數的定義，式(7)可重寫為

式(8)代入式(6)，可寫出

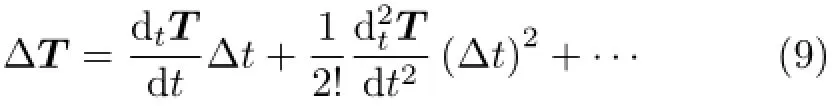
由式(9)右端的一階項，可以定義出拉格朗日時間域上張量場函數的微分dtT

確切地說，dtT是張量場函數T對時間t的微分。由于dtT是定義在物質點xm上的隨體概念，因此是“物質微分”。式(10)顯示，物質微分dtT是與物質導數dtT/dt對應的概念，二者之間成正比例關系，比例系數為dt。

如果dtT/dt是虛物質導數，則dtT就是虛物質微分。此時就將dtT稱為“張量場函數T的局部變分”。

式(10)中的定義可推廣到任意場函數。也就是說，任意場函數的局部變分，都可以通過其虛物質導數來定義。

虛物質導數dtT/dt和局部變分dtT，是張量變分學的基礎性概念。這兩個概念定義之后，張量變分學的理論體系，就大體上確定了。

8 張量場函數的經典微分與局部變分之間的對稱性

式(5)包含了兩個基本概念：拉格朗日空間域上，張量場函數T的偏導數?T/?xm和微分dT。式(10)也包含了兩個基本概念：拉格朗日時間域上，張量場函數T的虛物質導數dtT/dt和局部變分dtT。

空間域xm與時間域t是對應的。空間域與時間域上成對兒的基本概念，存在“一一對應”的對稱性

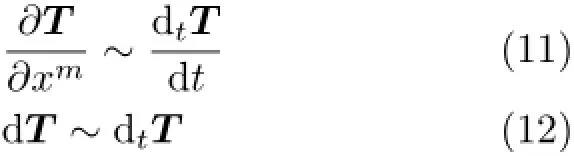
上述對稱性，既包含表觀形式的對稱，也包含解析結構的對稱。畫出如下對稱示意圖

注意到概念“名稱”的對稱性：dT是微分，dtT是變分。繼續類比，?T/?xm是微商，即微分之商；dtT/dt是變商，即變分之商。

至此，“張量的經典微分～張量的局部變分”之間的對稱性，就被建立起來了。這兩個概念極具基礎性。基于這兩個基礎性的概念，可以發展出來更多的概念、思想和理論。于是，一個有趣的問題值得追問：兩個基礎性概念之間對稱性“基因”，能否穩定地被“遺傳”下去？或者說，后繼的概念、思想和理論，能否葆有對稱性？答案是肯定的。

如上所述，基于偏導數?T/?xm和微分dT，可以發展張量場函數的微分學；基于虛物質導數dtT/dt和局部變分dtT，可以發展張量場函數的變分學。可以預料，張量變分學與張量微分學，也是對稱的，即

可以肯定，對于張量微分學中的表達式，張量變分學中都存在與之對稱的表達式。

9 拉格朗日基矢量的經典微分和局部變分之間的對稱性

任何成熟的理論都必須具有可計算性。從哪個角度審視張量變分學的可計算性？為便于參照，仍然從對稱的角度看問題。回顧一下張量微分學，可知有如下命題：基矢量微分的可計算性，是張量微分學可計算性的基礎。拉格朗日協變基矢量gi和逆變基矢量gi的函數形態為

張量微分學中，有著名的克里斯托弗爾公式[1-2]

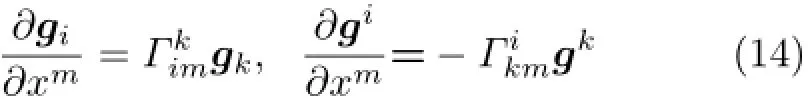
空間域上，克里斯托弗爾公式刻畫了拉格朗日基矢量的空間變化率。基矢量的空間導數，仍然是基矢量的組合，組合系數是Γkim。克里斯托弗爾公式是張量微分學的重要基礎之一。Γkim被稱為克里斯托弗爾符號。克里斯托弗爾符號的定義，是克里斯托弗爾對張量微分學的偉大貢獻。

基于式(14)，可導出基矢量的經典微分

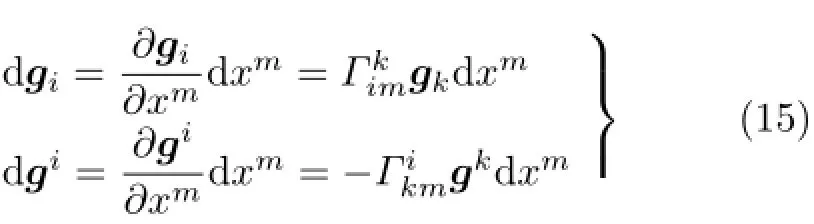
基矢量的空間微分dgi，仍然是基矢量gk的組合，組合系數是

可以從歷史中獲得借鑒：基矢量局部變分的可計算性，是張量變分學可計算性的基礎。時間域上，拉格朗日基矢量的物質導數為[1]

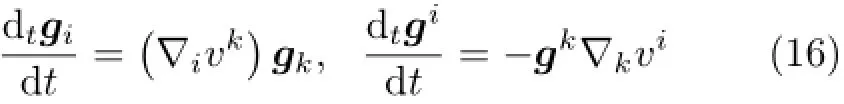
式中，vi是速度場矢量v=vigi的拉格朗日逆變分量。式(16)是張量分析學中的經典結果。基矢量的物質導數，仍然是基矢量的組合，組合系數是速度分量vk的協變導數(或速度梯度?v的分量)?ivk。

如果速度場v是“虛”的，則式(16)給出了基矢量的虛物質導數。顯然，拉格朗日基矢量的虛物質導數，取決于虛速度場的梯度?v。

式(16)與式(14)顯示出對稱性。與式(14)在張量微分學中的基礎性地位類似，式(16)是張量變分學的重要基礎。基于式(16)，可導出基矢量的局部變分

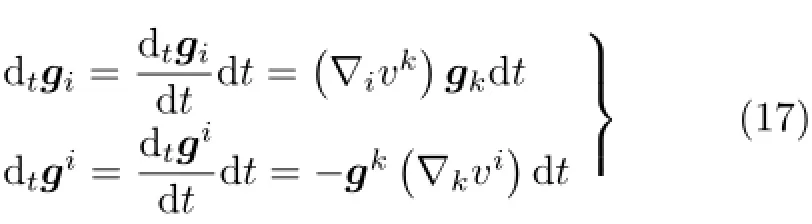
基矢量的局部變分dtgi，仍然是基矢量gk的組合，組合系數是(?ivk)dt。

一旦確定了虛速度梯度分量?ivk，則張量變分學中的任何計算，都可順利地給出確定的“值”。

從式(16)和式(17)中可獲得啟示：如果看到的是實速度場，那么，式(16)就給出了基矢量的實物質導數，式(17)就給出了基矢量的“實”時間微分。如果看到的是虛速度場，那么，式(16)就給出了基矢量的虛物質導數，式(17)就給出了基矢量的“虛”時間微分(或虛物質微分)，亦即局部變分。總之，只要速度場有虛實之分，基矢量的物質導數就有虛實之分，基矢量的時間微分就有虛實之分。而虛的時間微分，就是局部變分。

式(17)與式(15)之間的對稱性，清晰可見。

限于論文的篇幅，這里不再繼續展示張量變分學與張量微分學的對稱性。如果讀者有興趣，可以自己嘗試一下：比照張量微分學的大廈，一定可以構筑出張量變分學的大廈，且兩座大廈遙相呼應，構成優雅對稱的建筑群。

10 張量概念中的協變性思想及其推廣

對稱性的遺傳進程連綿不斷，當然也可以持續追問：對稱的張量微分學和張量變分學之后，是否還能塑造出更宏大的對稱建筑群？

答案是肯定的。但要塑造出新的對稱建筑群，必須先引入一塊厚重的基石--協變性思想。理由如下。

標題中，出現了張量一詞。實際上，即使沒有張量這個詞，本文照樣言之成理。之所以畫蛇添足地加上這個詞，是為后續建筑群的對稱化做鋪墊。

數學力學的歷史上，張量概念的誕生是件大事。不同于經典力學概念，張量概念中蘊涵了一個既漂亮又深刻的思想--協變性思想。

1935年，法國誕生了著名的布爾巴基學派。該學派提出了重要的思想觀念--數學結構。在諸種類型的數學結構中，最基本的是代數結構。張量就是普遍存在于物理學和力學中的代數結構。

作為代數結構，張量有內部子結構，例如，分量和基矢量。子結構滿足特定的協調約束性質，即“協變性”，具體表現為兩大基本變換：一是指標升降變換，二是坐標變換。作者將二者合稱為里奇變換[3-4]。

確切地說，協變性就是張量在里奇變換下的不變性。正是協變性，保證了張量的坐標無關性。從這個意義上講，在物理學和力學中，協變性近乎于客觀性。因此說，協變性思想，不僅漂亮，而且深刻。

從張量代數學到張量微分學的演進，是數學物理和數學力學史上的大事。但這件大事總被一種不大圓滿的氛圍所籠罩--張量微分的協變性退化了。喪失了協變性的張量微分，對物理學和力學不吝一場災難。

危難時刻，意大利的里奇學派盡顯英雄本色：他們巧妙地引入了漂亮的新概念--張量的協變微分，從而一舉將不協變的微分學，“美化”成了協變的微分學。

然而，隨著協變微分概念的誕生，概念上新的對稱性破缺出現了。隨著協變微分學的出世，理論上新的對稱性破缺出現了。

本文刻畫了這樣的歷史軌跡：先驅們定義了張量微分，造成了概念上的對稱性破缺。而隨著張量變分的定義，概念上的對稱性破缺得以彌補。先驅們發展了張量微分學，造成了理論上的對稱性破缺。而隨著張量變分學的建立，理論上的對稱性破缺得以修復。

現在，新的對稱性破缺引出了新的問題：還能重復上述對稱化歷史的軌跡嗎？答案是肯定的。對稱的建筑群將被持續延拓，規模更大、更為壯麗的對稱建筑群將拔地而起。如果讀者想一睹其真容，那就請閱讀后續文章吧。

11 說不盡的對稱

結束本文時，再關注一下對稱性。對稱是自然科學永恒的主題。歷史上，很多偉大學者都涉及過這個主題，例如，赫爾曼·外爾的《對稱》。當然，作者最喜歡前輩力學家武際可先生的對稱性思想。他的文集《動腦筋·說力學》[5-6]中，有兩篇文章涉及對稱，一是“談談對稱”，二是“從太極圖說起--再談對稱”。兩篇文章深入淺出，娓娓道來對稱思想之精髓，令人大開眼界，受益無窮。

讀者一定會問：“為什么對稱觀念如此令人著迷？”德國數學家諾特有著名的命題：任何對稱性，都對應著某種形式的守恒律。物理學和力學的歷史已經確證了命題的正確性：物理學和力學的每一條規律，都受到某種對稱性的支配；任何新對稱性的發現，都意味著新規律的誕生；任何對稱性破缺的出現，都意味著新理論的曙光。諾特的命題極大地消減了探索的盲目性--只要捕捉到對稱性，就可以順藤摸瓜地找到守恒律。本來，追尋守恒律，是物理學和力學探索者永恒的使命。諾特命題之后，追尋對稱性，成為物理學和力學探索者達成使命的捷徑。

這也正是作者在本文中的動機之所在：苦心孤詣地塑造經典微分與局部變分之間的對稱性。

12 結論

結束本文時，作者拋出一個疑問：虛物質導數是不可或缺的概念嗎？實際上，早在2016年，作者就直接從實物質導數出發，引出了局部變分概念。當時，沒有感到有何不妥之處。從前幾年的探索看，似乎有實物質導數概念就足夠了。這樣看來，虛物質導數概念似乎有些多余。引入虛物質導數，似乎違反了“奧卡姆剃刀”原則：如非必須，勿加實體。

后來，作者否定了“多余”的判斷。作者并不是想通了，而是類比之余，堅定了信念：已經有實位移，但從沒有認為，虛位移概念是多余的。已經有實速度，但從沒有認為，虛速度概念是多余的。已經有實加速度，但從沒有認為，虛加速度概念是多余的。

換個角度看：如果說，張量的局部變分是個不可或缺的概念，那么虛物質導數，就是個必不可少的概念。虛物質導數和局部變分概念的威力，會在后續的文章中，充分地展現出來。

本文只涉及了拉格朗日描述。歐拉描述，照樣可以揭示出對稱的張量微分學和張量變分學。換言之，張量微分學與張量變分學之間的對稱性，是一種客觀實在，與運動的描述方式無關。不論采用何種運動描述方式，對稱性都存在。但限于篇幅，本文不再涉及歐拉描述。

在傳統觀念中，張量分析學主要是指張量微分學。現在，可以更新觀念：張量分析學包括了兩個對稱的理論體系：一個是張量微分學，另一個是張量變分學。

本文講述了一個對稱性故事，后續文章將講述對稱性故事的續集。