“強基計劃”數學專題講座（四）
——“強基”數學試題中的數學演繹之美賞析

■江蘇省建湖高級中學 楊海濤

■江南大學理學院 謝廣喜

演繹其實是化歸與轉化思想方法的一種重要的具體表現形態,不過演繹方法更側重于由一般到特殊的推理,更注重于將典型的基本結論應用于具體問題的情境下解決問題,因此這些問題又往往與數學歷史名題交織在一起,比如我們熟知的錯位排列問題、費爾馬點、彭賽列問題、阿基米德三角形、阿波羅尼斯圓等。下面舉例說明。

例1(2019 年中國科學技術大學自主招生試題)設n是正整數,證明:存在多項式P(x),使得cosnθ=P(cosθ)。

解析：為表示方便起見,我們記與cosnθ(n∈N*)對應的多項式為Pn(cosθ)。容易取P1(cosθ)=cosθ,P2(cosθ)=cos 2θ=2cos2θ-1,即當n=1,2時,命題成立。

利用第二數學歸納法,假設1≤n≤k,命題都成立,則當n=k+1 時,有cos(k+1)θ=cos(kθ+θ)=coskθcosθ-sinkθsinθ=Pk(cosθ)P1(cosθ)-sinkθsinθ。

由于相同變量兩個多項式的乘積仍然是這個變量的多項式,故上面的表達式第一部分已滿足要求,下面的關鍵在于第二部分的處理。

而我們注意到其中的sin(k-1)θsinθ=-cos kθ+cos(k-1)θcosθ=-Pk(cos θ)+Pk-1(cos θ)P1(cosθ),cos(k-1)θsin2θ=Pk-1(cos θ)sin2θ,從 而cos(k+1)θ=Pk(cosθ)P1(cosθ)-[-Pk(cos θ)P1(cosθ)+Pk-1(cosθ)cos2θ+Pk-1(cos θ)sin2θ],也 即cos(k+1)θ=2Pk(cos θ)P1(cosθ)-Pk-1(cosθ)。

所以,當n=k+1時,命題也成立,于是對于任意的正整數k,命題恒成立。

評注:本題的命題背景是切比雪夫多項式(Chebyshevpolynomials)。一般地,?n∈N*還有遞推公式Pn+2(cosθ)=2Pn+1(cosθ)cosθ-Pn(cosθ),它在高等數學背景下著有非常廣泛的應用,比如函數逼近理論、信號的濾波等,在人工智能的神經網絡中可以作為有關圖的卷積核等。

例2(2019 清華大學自主招生試題第10題)設a為4 4444444各位數字之和,b為a各位數字之和,c為b各位數字之和,求c的值。

解析：任意一個十進制正整數N可記為,其中ai∈{0,1,2,3,…,9},且an≠0,也即N=an·10n+an-1·10n-1+an-2·10n-2+…+a1·10+a0。

易知N≡an+an-1+an-2+…+a1+a0(mod 9)。為表述方便,我們引入同余符號(≡),它常被用來表示兩個整數除以同一個正整數時具有相同余數的情況。比如,我們注意到4 444=9×493+7,所以4 444和7除以9(稱模9,在表達式中用mod 9表示)具有相同的余數,可簡為4 444≡7(mod 9)。完全類似地,我們容易利用二項式定理直接驗證,對于任意大于等于2的整數m,?n∈N*,有(m+1)n≡1(modm)成立。因此,結合題意得4 4444444≡a≡b≡c(mod 9)。

而4 4444444≡7(mod 9),于是有4 4444444≡74444(mod 9)≡(73)1481·7≡1×7≡7(mod 9)。

進而有4 4444444≡a≡b≡c≡7(mod 9),下證c≤12,顯然,如果非負整數c≤12,則由c≡7(mod 9)知c=7。

注意到4 444×3=lg 1 0004444＜lg4 4444444＜lg10 0004444=4×4 444=17 776,所以由a的含義知,a＜9×(17 776+1)=159 993。若a是六位數,則b≤1+4+9×4=41;若a的位數小于六位數,則b≤5×9=45。

所以,總有b≤45,進而可知b的各位數字之和最大時b為39,也即1≤c≤12。

再利用此過程中,a,b,c是模9 的不變量,則c=7。

評注:本題源自第17屆國際數學奧林匹克試題。

例3(2017年清華大學數學試題)正整數1,2,3,…,n的全排列(a1,a2,…,an)滿足ai≠i(i=1,2,3,…,n),稱為n項更列,記n項更列的個數為xn,下列命題中正確的是( )。

解析：n項更列也稱n項錯排問題。很顯然,對于B選項,我們取n=3,易算得x3=3! -1=5,而另一方面,我們直接用枚舉法可知x3=2,于是B 選項錯。設k個元素的錯排有D(k)個,n個元素的錯排時,顯然元素n只有n-1個排法(因為元素n不能放置在第n個位置上),對應其排于某個具體位置i(i≠n),此時若元素i置于位置n,則余下的問題轉化為n-2個元素錯排問題,有D(n-2)個。若元素i未置于第n個位置,則此時可把元素i當成元素n,余下問題變為n-1個元素錯排問題,有D(n-1)個。

于是有D(n)=(n-1)[D(n-2)+D(n-1)]。

評注:本題實質上就是數學史上有名的“錯位排列”或“裝錯信封”問題。

【創新有源泉、經典永流傳】

1.(2021 年全國高考甲卷理科數學試題)拋物線C的頂點為坐標原點O,焦點在x軸上,直線l:x=1交拋物線C于P,Q兩點,且OP⊥OQ。已知點M(2,0),且☉M與直線l相切。

(1)求拋物線C,☉M的方程;

(2)設A1,A2,A3是拋物線C上的三個點,直線A1A2,A1A3均與☉M相切,判斷直線A2A3與☉M的位置關系。

簡解：(1)依題意設拋物線C:y2=2px(p＞0),P(1,y0),Q(1,-y0)。

因為OP⊥OQ,所以=1-2p=0,解得2p=1。

所以拋物線C的方程為y2=x。

☉M與x=1 相切,所以半徑為1,即☉M的方程為(x-2)2+y2=1。

(2)設A1(x1,y1),A2(x2,y2),A3(x3,y3),為節省篇幅,直線A1A2,A1A3,A2A3中部分斜率不存的情況,此處從略,同學們可自行證明。下面假設若直線A1A2,A1A3,A2A3斜率均存在,則

所以直線A1A2的方程為y-y1=),整理得x-(y1+y2)y+y1y2=0。

同理,直線A1A3的方程為x-(y1+y3)y+y1y3=0。

直線A2A3的方程為x-(y2+y3)y+y2y3=0。

所以直線A2A3與圓M相切。

綜上所述,若直線A1A2,A1A3與圓M相切,則直線A2A3與圓M也相切。

評注:本題背景稱為彭賽列問題,三者相切,如何簡捷地完成最后一步演繹推理是求解問題的核心和關鍵。不少同學反映答案能看懂,但自己做思路卻亂七八糟,這里我們充分利用(逆用)一元二次方程根與系數的關系,最后比較簡捷地給出一個邏輯分明的思路(而且此思路具有相對一般性),供大家參考。

2.(2020 年江蘇高考數學試題)甲口袋中裝有2個黑球和1個白球,乙口袋中裝有3個白球。現從甲、乙兩個口袋中各任取1 個球交換放入另一個口袋,重復n次這樣的操作,記甲口袋中黑球個數為Xn,恰有2 個黑球的概率為pn,恰有1個黑球的概率為qn。

(1)求p1,q1和p2,q2;

(2)求2pn+qn與2pn-1+qn-1的遞推關系式和Xn的數學期望E(Xn)(用n表示) 。

簡解：本題的難點在于重復操作后,每一次當前狀態的概率(pn,qn)依賴于上一次狀態的概率(pn-1,qn-1),然而系統每一次的具體狀態又有多種可能,所以同學們需要以上一次狀態概率(pn-1,qn-1)為基準,建立其與當前狀態的概率(pn,qn)之間的遞推關系。注意到甲、乙兩個口袋中一共僅有2個黑球,故一般情況下黑球的所在位置(對應問題的可能狀態,因為黑球給定,白球自動確定,下面將不一定再強調白球的數目)有三種可能:①甲袋里有2個;②甲、乙兩個口袋里有各1個;③乙袋里有2個。

具體研究如下。

(1)①先求p1和q1,聯合簡記為(p1,q1),p1的含義是一次交換后黑球沒有變動(即2個黑球仍然都在甲口袋)的概率,即甲口袋選中交換的球是白球,概率顯然為

此時所有狀態只有兩種可能:要么甲袋里有2個黑球;要么甲袋里有1 個黑球。于是可得

②求(p2,q2)就不是十分容易了,此時必須注意到,實際上一般情形每個狀態是有三種可能這個關鍵環節(這一點非常重要,因為它為下一步問題的求解奠定了基礎),為了理解方便,我們形象地用表1表示。必須指出,當n=1 時,才有pn+qn=1;當n≥2 時,pn+qn＜1。

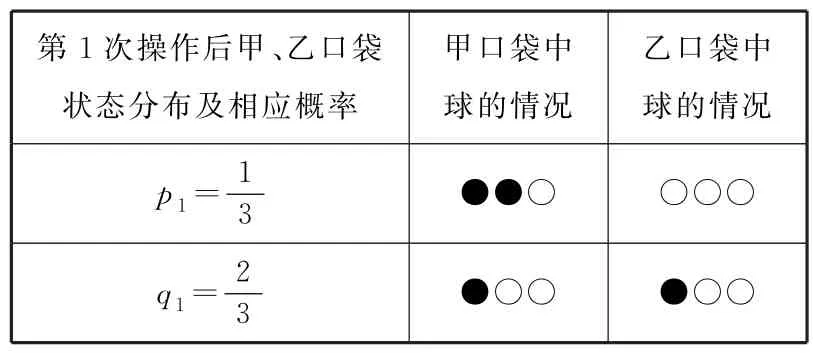
表1

此時,要求(p2,q2)。比如求p2,可能是在p1概率前提下,甲、乙兩個口袋分別取1個白球交換的結果;也可能是在q1概率前提下,甲口袋中的取到白球(同時乙口袋取到黑球)的結果。于是

完全類似地,要求q2,可能是在p1概率前提下,甲口袋取中1個黑球(同時乙口袋取到白球)交換的結果;也可能是在q1前提下,甲、乙兩個口袋中同時取到黑球(或同時取到白球)的結果。

(2)當n≥2時,由題意可得第n次操作后狀態分布及相應的概率如表2所示。

表2

根據此表,結合(pn+1,qn+1)的具體含義,容易得到:

評注:本題的摸球法是概率論問題研究中的一種經典模型方法。

3.(2011 年“北約”試題第2 題改編)過拋物線y=2x2-2x-1與y=-5x2+2x+3交點的直線方程為____。

簡解：本題如果求出兩條曲線的交點,過程是比較麻煩的。在我們對此問題深入思考之后,發現若用曲線系的思路求解,則異常簡捷。過這兩條拋物線y=2x2-2x-1與y=-5x2+2x+3交點(如果交點存在的話)的曲線系可記為λ1(y-2x2+2x+1)+λ2(y+5x2-2x-3)=0。我們希望其表示過焦點的直線,即只要其中僅有的二次項x2系數-2λ1+5λ2=0。不妨令λ1=5,λ2=2,代入曲線系可得7y+6x=1,這正是經過兩條拋物線交點的直線方程。

評注:由題意知兩條曲線的交點存在,故上面的求解過程也是可以的(除非交點根本就不存在)。當然,如果是解答題,嚴格來說,以此直線分別與兩條曲線聯立,反向驗證一下交點的存在性,則更好一些!

4.(2010年安徽省賽題第5 題)設z為復數,則|z-1|+|z-i|+|z+1|的最小值為____。

簡解：記復數z=x+yi(x,y∈R),則我們可以通過數形結合,將原問題等價轉化為平面直接坐標系中,求點P(x,y)與點A(1,0),B(-1,0),C(0,1)距離之和的最小值。

此時這個最小值對應點P(x,y)的位置正是△ABC的費爾馬點,于是容易得到相應的最小值為

評注:本題是費爾馬點背景的問題。