國家數(shù)值風(fēng)洞(NNW)通用軟件同構(gòu)混合求解器設(shè)計

陳堅強(qiáng), 馬燕凱, 閔耀兵, 趙 鐘, 何先耀, 何 琨

(中國空氣動力研究與發(fā)展中心 計算空氣動力研究所, 綿陽 621000)

0 引 言

計算流體力學(xué)(Computational Fluid Dynamics，CFD)，是當(dāng)前飛行器設(shè)計過程中，用以獲得氣動數(shù)據(jù)的重要手段，已從早期的僅用于校驗輔助設(shè)計，發(fā)展到能為設(shè)計包線中的部分狀態(tài)直接提供氣動數(shù)據(jù)。然而，盡管近二三十年來，CFD發(fā)揮的作用在持續(xù)增加，但計算結(jié)果可信度僅局限于無大分離流動的巡航狀態(tài)(圖1)[1]，而在飛行包線的邊緣區(qū)，仍然存在較大的不確定度。

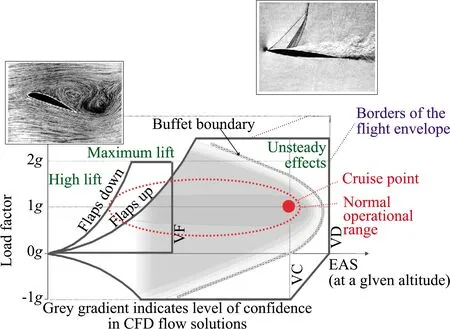
圖1 CFD在飛行包線中發(fā)揮的作用[1]

造成此種窘境的關(guān)鍵因素之一，在于當(dāng)前使用“單一”的CFD方法模擬“復(fù)雜”的非線性流動：(1)單一的網(wǎng)格類型。不管是廣泛使用的In-House代碼，還是通用商業(yè)CFD軟件，都采用單一的網(wǎng)格類型，要么是基于結(jié)構(gòu)網(wǎng)格、要么是基于非結(jié)構(gòu)網(wǎng)格，相應(yīng)的CFD求解器也只能是二選一。(2)單一的精度。當(dāng)前工程中廣泛應(yīng)用的CFD軟件，基本都是二階精度，受限于高階精度方法較低的健壯性，高階精度方法還難以在工程中成熟應(yīng)用。(3)單一的學(xué)科。大多是求解僅考慮空氣動力學(xué)完全氣體效應(yīng)的流動模擬。(4)單一的物理模型。鑒于直接數(shù)值模擬方法(DNS)和大渦模擬方法(LES)的巨量計算資源需求，工程中一般采用全湍流的雷諾平均NS方法(RANS)。

然而，現(xiàn)實中的空氣動力學(xué)卻是“多元”的：(1)多元的網(wǎng)格。相對結(jié)構(gòu)網(wǎng)格，雖然因非結(jié)構(gòu)網(wǎng)格生成難度的降低而應(yīng)用越來越多，但在高超聲速、高精度等對網(wǎng)格質(zhì)量要求較高的領(lǐng)域，由于結(jié)構(gòu)網(wǎng)格具有計算效率高、對邊界層的模擬更精確、易于處理各向異性網(wǎng)格等優(yōu)勢，依然有其存在的價值，二者仍將共存，且在各自領(lǐng)域發(fā)揮自身的優(yōu)點。(2)多元的精度。當(dāng)前，越來越多的高精度方法研究者意識到，即使在將來，高精度方法仍無法完全替代二階精度方法，而是互補(bǔ)的關(guān)系。高精度方法在大分離流動、強(qiáng)間斷等關(guān)鍵流動區(qū)域扮演關(guān)鍵角色，而二階方法在巡航等常規(guī)狀態(tài)模擬中具有較高的性價比。(3)多學(xué)科模擬。真實飛行環(huán)境中往往涉及“聲、光、電、磁、熱”等多學(xué)科耦合，單一的流體力學(xué)學(xué)科難以準(zhǔn)確地模擬真實環(huán)境，毋庸置疑，未來的CFD必定是多學(xué)科耦合模擬。(4)多元的物理模型。由于復(fù)雜流動中伴隨層流、轉(zhuǎn)捩、湍流、大范圍分離等多種流動，采用單一的湍流模擬方法要么性價比低，要么難以準(zhǔn)確捕捉流場結(jié)構(gòu)，而在不同區(qū)域采用不同的湍流模擬方法，是一種現(xiàn)實可行的求解策略。

采用“混合求解器”，是解決當(dāng)前的“單一”化與“多元”化需求矛盾的有效途徑之一。混合求解器，即在不同的區(qū)域，采用不同的求解器，發(fā)揮各自的優(yōu)勢，以實現(xiàn)有工程價值的復(fù)雜CFD模擬。例如，不同網(wǎng)格類型的混合求解，不同精度的混合求解，不同學(xué)科的混合求解。

早在20世紀(jì)90年代，就有研究者實現(xiàn)了結(jié)構(gòu)/非結(jié)構(gòu)網(wǎng)格的Euler混合計算[2]，應(yīng)用于飛機(jī)外形，通過在兩種類型網(wǎng)格的交界面上采用拼接網(wǎng)格，實現(xiàn)信息交換。2010年，研究者用混合計算方法模擬氣動聲學(xué)的多學(xué)科問題，在笛卡爾直角網(wǎng)格上采用有限差分法，在非結(jié)構(gòu)網(wǎng)格上采用高階間斷有限元(DG)方法，以實現(xiàn)不大幅增加計算量的前提下，完成對復(fù)雜外形的高精度模擬[3-4]。知名In-House CFD代碼elsA-Hybrid，原本是一款采用多塊結(jié)構(gòu)網(wǎng)格、基于有限體積方法的求解器elsA，為了充分利用結(jié)構(gòu)網(wǎng)格高效高精度和非結(jié)構(gòu)網(wǎng)格靈活性的優(yōu)點，采用面向?qū)ο缶幊蹋谠械慕Y(jié)構(gòu)求解代碼基礎(chǔ)上增加了非結(jié)構(gòu)求解模塊，開發(fā)了新一代混合求解器elsA-Hybrid[5-6]，實現(xiàn)了三維高升力外形、翼身組合體等外形的二階混合模擬，兩種求解算法盡可能做到代碼的統(tǒng)一，例如在通量計算層次基本實現(xiàn)了代碼統(tǒng)一，基本實現(xiàn)了在細(xì)粒度層面的混合求解。在空間計算域融合方面，在作為CREATE-AV子項之一的Helios軟件系統(tǒng)中[7]，對旋翼類外形(圖2)，Helios在空間中采用不同的網(wǎng)格類型離散，分別調(diào)用不同類型的求解器，如在外場空間笛卡爾網(wǎng)格上調(diào)用SAMARC求解器，在旋翼附近調(diào)用結(jié)構(gòu)求解器OverFLOW，在機(jī)身附近調(diào)用非結(jié)構(gòu)求解器FUN3D，不同的求解器之間通過Python實現(xiàn)數(shù)據(jù)共享。作者所在團(tuán)隊也在此前開展了結(jié)構(gòu)/非結(jié)構(gòu)混合計算相關(guān)研究[8-9]。

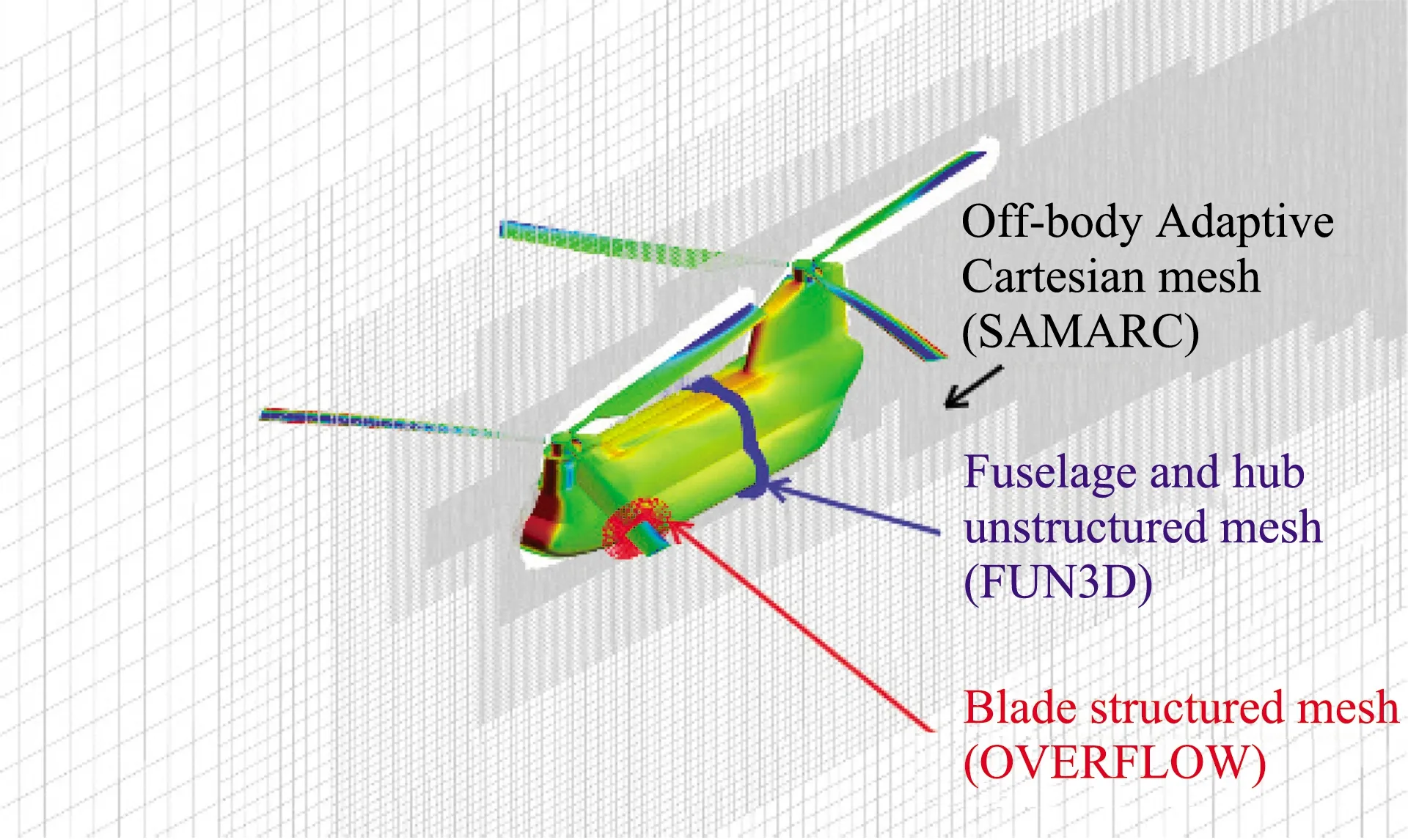
圖2 Create項目中的多求解器混合計算[7]

對于混合計算技術(shù)，目前通常有兩種不同的技術(shù)途徑。一種是“異構(gòu)”混合計算，以多求解器間松耦合為特征，如上面提及的CREATE中的Helios分系統(tǒng)；另一種是“同構(gòu)”混合計算，以多算法在同一個平臺上緊耦合模擬為特征，如上文提及的混合求解器elsA-Hybrid。“異構(gòu)”混合計算能很方便地集成已有軟件，開發(fā)成本低，風(fēng)險小。但因各求解器之間數(shù)據(jù)結(jié)構(gòu)不同，并行框架不相容，重復(fù)模塊多，使其可擴(kuò)展性、可維護(hù)性低。反之，“同構(gòu)”混合計算是在同一個框架上開發(fā)，在數(shù)據(jù)結(jié)構(gòu)、并行框架等方面都可以大量復(fù)用，因而效率高、可擴(kuò)展性、可維護(hù)性強(qiáng)。但因需統(tǒng)一多種求解器，因而風(fēng)險大、工作量大、難度大。“異構(gòu)”混合計算模式適用于集成存量，而“同構(gòu)”混合計算是一種面向下一代的CFD軟件的挑戰(zhàn)性模式。

“國家數(shù)值風(fēng)洞(NNW)”是我國正在自主研發(fā)的CFD軟件系統(tǒng)，目標(biāo)是建設(shè)國際領(lǐng)先的CFD高性能計算機(jī)系統(tǒng)，建成擁有自主知識產(chǎn)權(quán)、國內(nèi)開放共享、達(dá)到世界一流水平的空氣動力數(shù)值模擬平臺。“風(fēng)雷(PHengLEI)”軟件[10-11]，是NNW工程的通用CFD軟件，設(shè)計了面向結(jié)構(gòu)/非結(jié)構(gòu)的、適用于大規(guī)模并行的軟件架構(gòu)，其典型特色是可實現(xiàn)任意求解器的“同構(gòu)”混合計算，以解決未來多學(xué)科模擬中對“多元”化CFD模擬的需求。

WCNS高階精度有限差分方法由鄧小剛等人提出[12]并經(jīng)過二十多年的持續(xù)發(fā)展，其對于流動結(jié)構(gòu)的分辨能力較高[13]。在滿足幾何守恒律的基礎(chǔ)上[14-15]，WCNS方法在復(fù)雜網(wǎng)格計算中的適應(yīng)能力得以大幅提升。近年來，在全局守恒條件約束下，鄧小剛等人又發(fā)展了與內(nèi)點相匹配的WCNS邊界計算方法[16]。當(dāng)前制約WCNS高階方法應(yīng)用于工程復(fù)雜外形流動計算的主要難點在于高質(zhì)量的多塊對接結(jié)構(gòu)網(wǎng)格的生成，以及復(fù)雜邊界處理，其直接影響到計算魯棒性，是制約工程應(yīng)用推廣的瓶頸。

本文就PHengLEI軟件中的混合求解器，介紹了混合求解策略及軟件設(shè)計方法，并通過典型算例，驗證結(jié)構(gòu)/非結(jié)構(gòu)網(wǎng)格耦合求解、二階有限體積/WCNS高階耦合求解這兩類混合求解方法的可行性。有關(guān)PHengLEI軟件的整體架構(gòu)、并行方法，可參考文獻(xiàn)[10-11]。

1 域、交界面與數(shù)據(jù)交換

在正式介紹混合計算策略前，先介紹與混合計算緊密聯(lián)系的一些概念(如域、交界面)，以及相關(guān)的數(shù)據(jù)結(jié)構(gòu)。

1.1 域和交界面的抽象

CFD模擬一般基于計算網(wǎng)格進(jìn)行，整個計算域由多個計算區(qū)域組成，每個計算域被離散為若干網(wǎng)格單元。采用結(jié)構(gòu)網(wǎng)格時，首先用線、面將整體計算域劃分為多個子域，再在每個子域生成網(wǎng)格單元。采用非結(jié)構(gòu)網(wǎng)格時，雖然初始整體計算域作為一個整體存在，但是在并行計算時，一個計算域被分解為多個子域。我們將每個子域及其所屬的網(wǎng)格單元，定義為域(Zone)，不同域之間的交界面，定義為交界面(Interface)。圖3的示例中，整個計算域被劃分為2個域，Zone1和Zone2，為示普遍性，分別為非結(jié)構(gòu)和結(jié)構(gòu)網(wǎng)格，二者間是互不重疊且對接(點一一對應(yīng))的交界面。

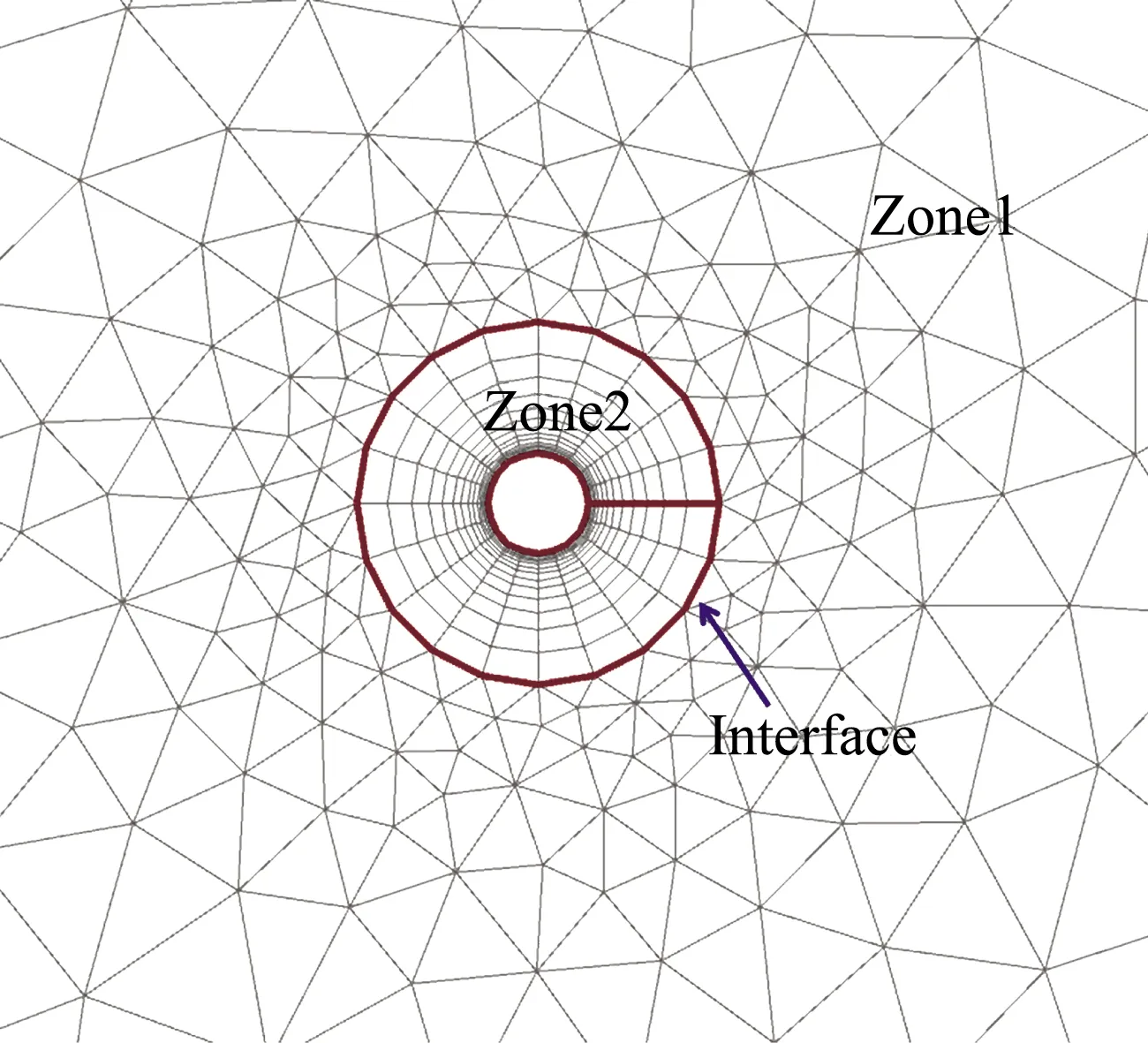
圖3 域與交界面

域，是混合計算中不同求解器的載體。在混合計算時，將在每個域上存儲各自的求解器。在每一迭代步中，遍歷所有的子域求解。

交界面，是混合求解器的核心。不同域(其上可能加載不同的求解器)間的數(shù)據(jù)交換，通過交界面實施。實際上，這里的交界面是廣義的，包含三種類型：

1)多塊結(jié)構(gòu)網(wǎng)格中，塊與塊之間的交界面；

2)非結(jié)構(gòu)網(wǎng)格中，并行計算分區(qū)后，分區(qū)之間的交界面；

3)在計算域中同時含有結(jié)構(gòu)、非結(jié)構(gòu)網(wǎng)格時，兩種網(wǎng)格類型間的交界面。

混合求解，即是每個交界面兩側(cè)的兩個單元(分別是結(jié)構(gòu)、非結(jié)構(gòu)網(wǎng)格單元)交換流場數(shù)據(jù)，進(jìn)而實現(xiàn)不同域之間耦合的過程。

1.2 數(shù)據(jù)結(jié)構(gòu)與信息交換

PHengLEI軟件中定義的“交界面”是以上三種類型的合集，即將三種交界面抽象為統(tǒng)一的“Interface”。無論是何種類型，都采用相同的數(shù)據(jù)結(jié)構(gòu)存儲、交換。因之，交界面的數(shù)據(jù)結(jié)構(gòu)是核心。

為此，風(fēng)雷軟件中設(shè)計了“三合一”的數(shù)據(jù)底層DataContainer，用于交換網(wǎng)格塊間的各類數(shù)據(jù)。任意數(shù)據(jù)經(jīng)DataContainer標(biāo)準(zhǔn)化為數(shù)據(jù)底層后，在完全相同的機(jī)制下實現(xiàn)以下“三合一”數(shù)據(jù)交換：

a)進(jìn)程內(nèi)的結(jié)構(gòu)多塊網(wǎng)格交界面數(shù)據(jù)交換；

b)進(jìn)程間的相鄰網(wǎng)格塊(既可以是結(jié)構(gòu)，也可以是非結(jié)構(gòu))交界面數(shù)據(jù)交換，主要用于MPI通信；

c)節(jié)點內(nèi)任意網(wǎng)格塊交界面數(shù)據(jù)交換，主要用于混合求解器計算。

數(shù)據(jù)標(biāo)準(zhǔn)化的原理很簡單：對于結(jié)構(gòu)、非結(jié)構(gòu)兩種不同的數(shù)據(jù)存儲結(jié)構(gòu)，將二者統(tǒng)一壓縮為字符型數(shù)據(jù)，以實現(xiàn)兩類數(shù)據(jù)的標(biāo)準(zhǔn)化[10]。

2 混合求解策略

下文以結(jié)構(gòu)/非結(jié)構(gòu)混合計算、二階/高階混合計算，說明混合求解器的耦合策略。

2.1 結(jié)構(gòu)/非結(jié)構(gòu)耦合策略

PHengLEI軟件框架既適應(yīng)于結(jié)構(gòu)網(wǎng)格、非結(jié)構(gòu)網(wǎng)格，還能實現(xiàn)結(jié)構(gòu)/非結(jié)構(gòu)網(wǎng)格下的求解器耦合計算。結(jié)構(gòu)/非結(jié)構(gòu)兩種求解器可獨立運行(即在流場中同時含有結(jié)構(gòu)網(wǎng)格和非結(jié)構(gòu)網(wǎng)格的情況下，在結(jié)構(gòu)網(wǎng)格上調(diào)用結(jié)構(gòu)求解器，在非結(jié)構(gòu)網(wǎng)格上調(diào)用非結(jié)構(gòu)求解器)，并能進(jìn)行結(jié)構(gòu)求解器和非結(jié)構(gòu)求解器的同步耦合計算。

結(jié)構(gòu)/非結(jié)構(gòu)耦合計算的關(guān)鍵技術(shù)是兩種類型網(wǎng)格交界面的數(shù)據(jù)通信。在兩種網(wǎng)格內(nèi)部分別調(diào)用結(jié)構(gòu)/非結(jié)構(gòu)求解器計算，兩種網(wǎng)格間的交界面形成各自求解器的邊界條件，將這種邊界條件抽象為InterFace類。在結(jié)構(gòu)網(wǎng)格和非結(jié)構(gòu)網(wǎng)格之間，通過交界面建立一一對應(yīng)的面映射關(guān)系(圖4)，計算模板相應(yīng)擴(kuò)展：對于結(jié)構(gòu)求解器，在內(nèi)場單元i處將另一側(cè)的非結(jié)構(gòu)網(wǎng)格體心值視為其虛擬單元(i+1)；對于非結(jié)構(gòu)求解器，在內(nèi)場單元le處將另一側(cè)的結(jié)構(gòu)網(wǎng)格體心值視為其虛擬單元(re)。對于結(jié)構(gòu)求解器，往往需要在邊界處拓寬虛擬單元模板，除了i+1點外，還需要i+2，……，i+n點信息，為簡便起見，混合計算時一般采用一層虛擬單元。

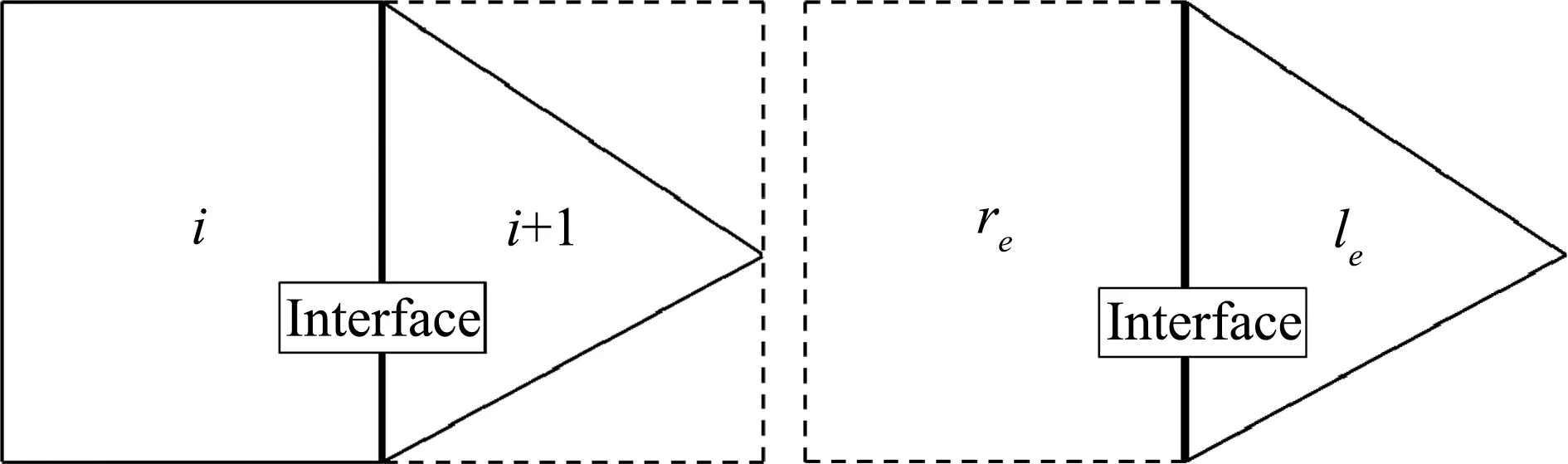
(a)結(jié)構(gòu)求解器模板 (b)非結(jié)構(gòu)求解器模板

結(jié)構(gòu)/非結(jié)構(gòu)網(wǎng)格交界面InterFace的處理方式和并行分區(qū)交界面、多塊結(jié)構(gòu)網(wǎng)格間交界面完全一樣，采用“三合一”數(shù)據(jù)底層進(jìn)行數(shù)據(jù)交換。在計算過程中，通過交界面交換流場變量q和梯度q。

2.2 二階/高階精度耦合策略

PHengLEI軟件框架中，二階/高階精度耦合策略是指，二階精度求解器采用結(jié)構(gòu)或非結(jié)構(gòu)的有限體積方法，高階精度求解器采用基于結(jié)構(gòu)網(wǎng)格的WCNS高階精度有限差分方法。研究表明[17]，WCNS求解器分辨率較二階有限體積求解器高，對關(guān)鍵流動結(jié)構(gòu)的模擬能力明顯優(yōu)于傳統(tǒng)的二階求解器。但WCNS高階精度計算方法對網(wǎng)格質(zhì)量要求較高，其適應(yīng)復(fù)雜外形計算的能力不如非結(jié)構(gòu)網(wǎng)格的二階求解器。二階非結(jié)構(gòu)解算器適用于復(fù)雜外形計算，但不具備WCNS高階精度求解器對流場結(jié)構(gòu)的分辨率。因此，從WCNS求解器工程實用化觀點看，在關(guān)鍵流動特征區(qū)域采用高質(zhì)量的結(jié)構(gòu)網(wǎng)格基于WCNS求解器計算，而在其他復(fù)雜區(qū)域采用非結(jié)構(gòu)網(wǎng)格基于二階精度非結(jié)構(gòu)求解器計算，使高階精度結(jié)構(gòu)求解器和二階精度非結(jié)構(gòu)求解器優(yōu)勢互補(bǔ)，不失為一種解決工程實際復(fù)雜問題的可行方案。

二階/高階精度求解器耦合策略與結(jié)構(gòu)/非結(jié)構(gòu)耦合策略相同，都是交換流場變量、梯度等(圖5)。

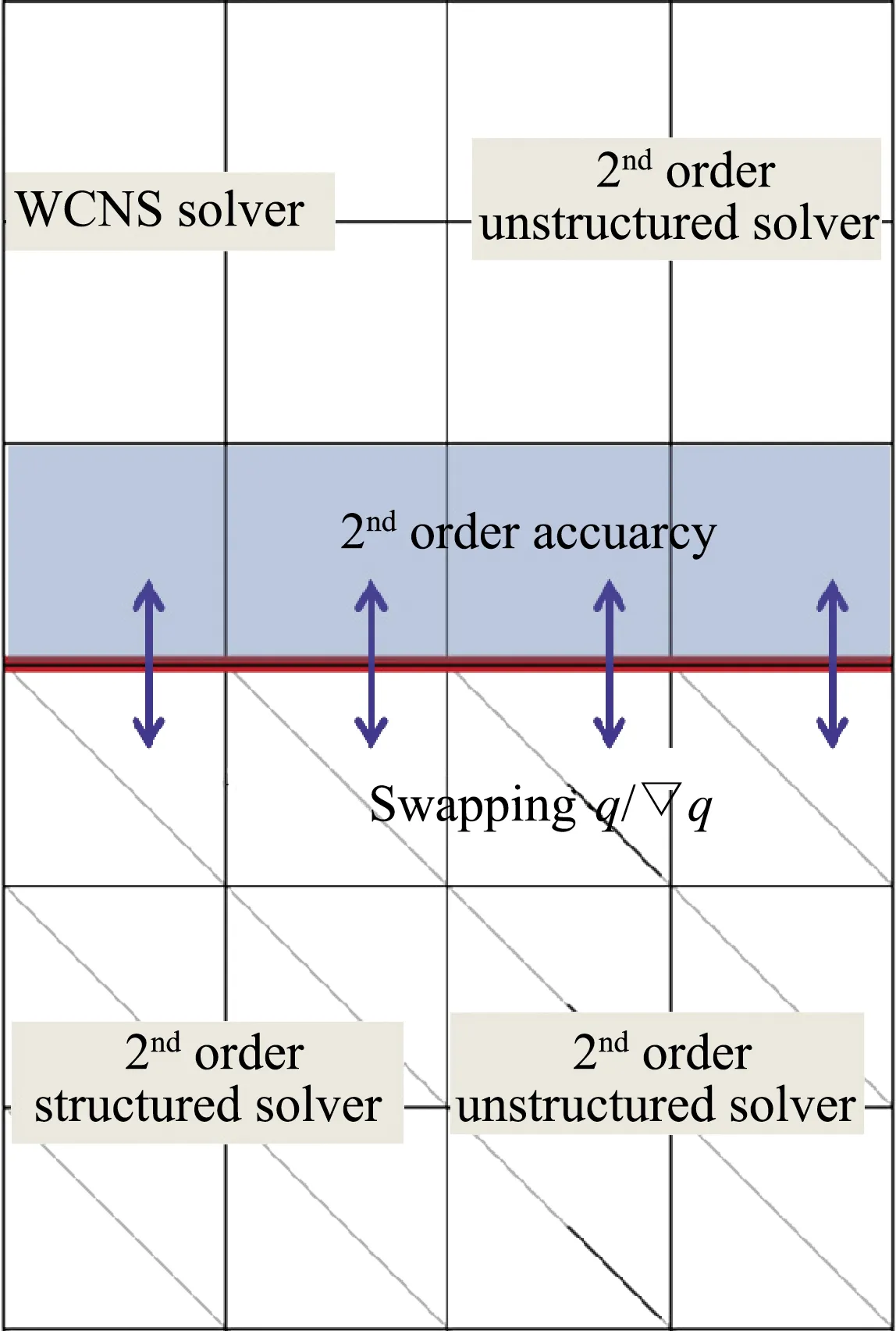
圖5 混合求解器信息交換

單一的WCNS求解器應(yīng)用于多塊網(wǎng)格時，需根據(jù)精度的需要，交換緊鄰交界面的多層單元數(shù)據(jù)(三階精度需交換2層)。很顯然，非結(jié)構(gòu)網(wǎng)格中由于沒有網(wǎng)格層，只向WCNS求解器提供1層信息，相當(dāng)于在交界面處退化為二階精度。實際上，對于混合求解器來說，在非結(jié)構(gòu)網(wǎng)格上已經(jīng)全部是二階精度，即使在結(jié)構(gòu)網(wǎng)格上有1層網(wǎng)格精度退化，也無大礙。

3 混合計算案例

為考察本文混合求解耦合策略的有效性，以二維圓柱和三維雙橢球的高超聲速黏性繞流為例，對二階非結(jié)構(gòu)/二階結(jié)構(gòu)混合計算、二階非結(jié)構(gòu)/高階WCNS混合求解方法可行性與正確性進(jìn)行驗證。

3.1 二維圓柱繞流

計算條件[18]：層流，來流馬赫數(shù)8.03，來流單位雷諾數(shù)1.835×105，來流溫度124.94 K，壁面溫度294.44 K。采用三套網(wǎng)格(圖6)進(jìn)行計算：第一套為結(jié)構(gòu)網(wǎng)格，網(wǎng)格數(shù)目為121×87(流線×法向)，采用結(jié)構(gòu)WCNS高階精度求解器；第二套是混合網(wǎng)格，將第一套網(wǎng)格劃分為內(nèi)外兩個塊得到，靠近壁面的是結(jié)構(gòu)網(wǎng)格，采用WCNS高階精度求解器，遠(yuǎn)離壁面的結(jié)構(gòu)網(wǎng)格被非結(jié)構(gòu)化，采用二階精度非結(jié)構(gòu)有限體積求解器(Unstr-FVM)；第三套是混合網(wǎng)格，將第二套網(wǎng)格中外場塊四邊形網(wǎng)格三角化得到，內(nèi)場結(jié)構(gòu)網(wǎng)格上依然采用WCNS高階求解器，外場三角形網(wǎng)格采用Unstr-FVM求解器。

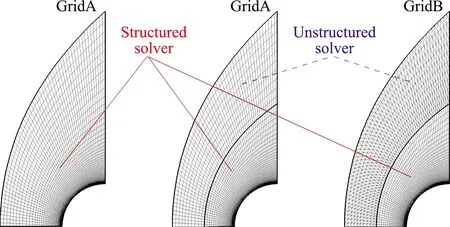
圖6 二維層流圓柱算例的網(wǎng)格分布及各區(qū)域所加載的求解器示意圖

這三套網(wǎng)格(三種計算策略)的目的是：第一套網(wǎng)格是全高精度計算，用于對比參考；第二套網(wǎng)格與第一套相同，僅僅是將四邊形非結(jié)構(gòu)化，用于比較混合求解器帶來的差異；第三套是混合網(wǎng)格、混合求解器，是測試的目的。

從計算收斂性看(圖7)，三套網(wǎng)格殘差均收斂至機(jī)器“零”，且收斂后的氣動力系數(shù)保持一致。從物面壓力和熱流分布看(圖8)，三套網(wǎng)格上的結(jié)果幾乎重合，混合計算與全結(jié)構(gòu)網(wǎng)格WCSN高階精度模擬結(jié)果相差無幾。該算例表明，混合計算既能保持高精度格式的方法，又適應(yīng)非結(jié)構(gòu)網(wǎng)格。

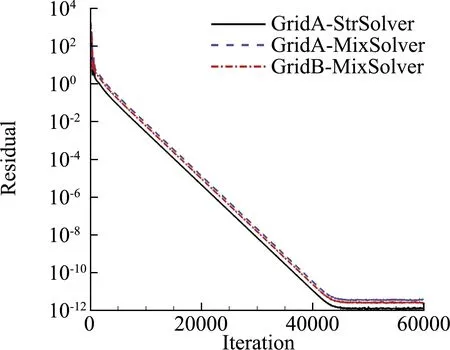
(a)殘差

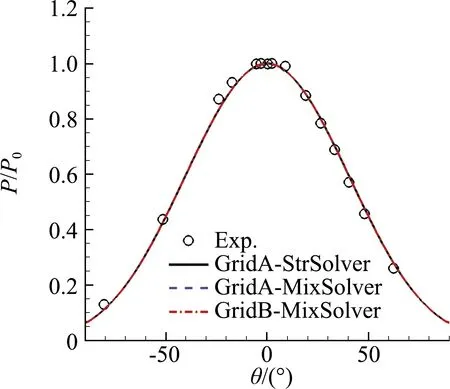
(a)壁面壓力分布

3.2 雙橢球繞流

雙橢球繞流是典型的高超聲速模擬算例[19-21]。計算條件為：層流，0°攻角，來流馬赫數(shù)8.15，來流單位雷諾數(shù)1.67×107，來流溫度56 K，壁面溫度288 K，不考慮底部流動。采用兩套網(wǎng)格計算(圖9)：第一套為純結(jié)構(gòu)網(wǎng)格，根據(jù)流場特點對強(qiáng)激波、激波與邊界層干擾、激波與激波干擾的區(qū)域進(jìn)行了局部網(wǎng)格加密，網(wǎng)格總數(shù)為468萬，運行WCNS高階精度求解器；第二套是結(jié)構(gòu)/非結(jié)構(gòu)混合網(wǎng)格，壁面附近為結(jié)構(gòu)網(wǎng)格，運行WCNS求解器，遠(yuǎn)離壁面區(qū)域為非結(jié)構(gòu)網(wǎng)格，運行二階精度非結(jié)構(gòu)有限體積求解器(Unstr-FVM)。

(a)純結(jié)構(gòu)網(wǎng)格

從殘差收斂看(圖10)，WCNS/FVM混合求解器能保持純WCNS高階求解器的收斂性。圖11是兩種求解器計算所得的表面極限流線，混合求解器保持了WCNS高階求解器對二次分離流的清晰捕捉能力。

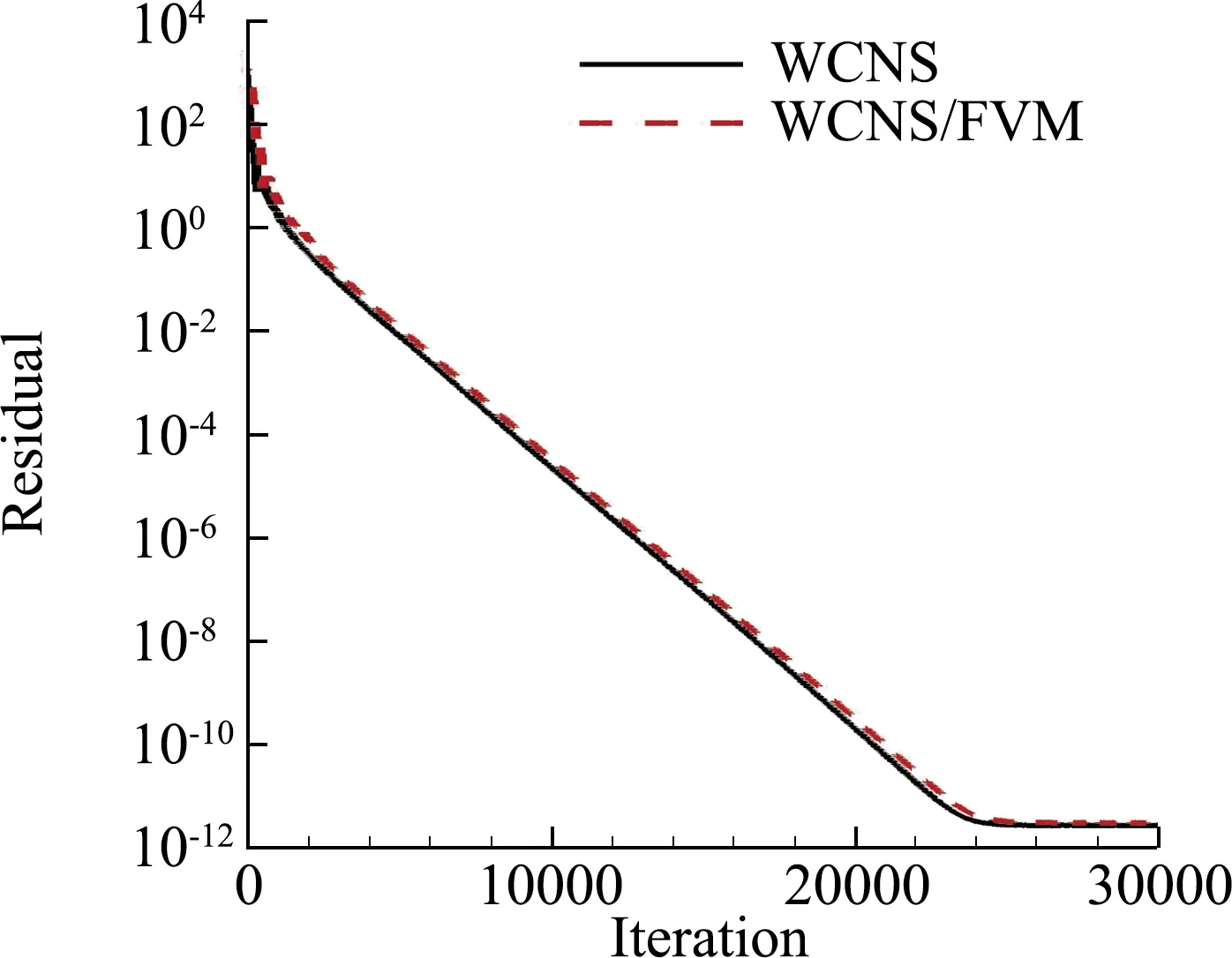
圖10 混合求解器與純高階求解器殘差收斂對比

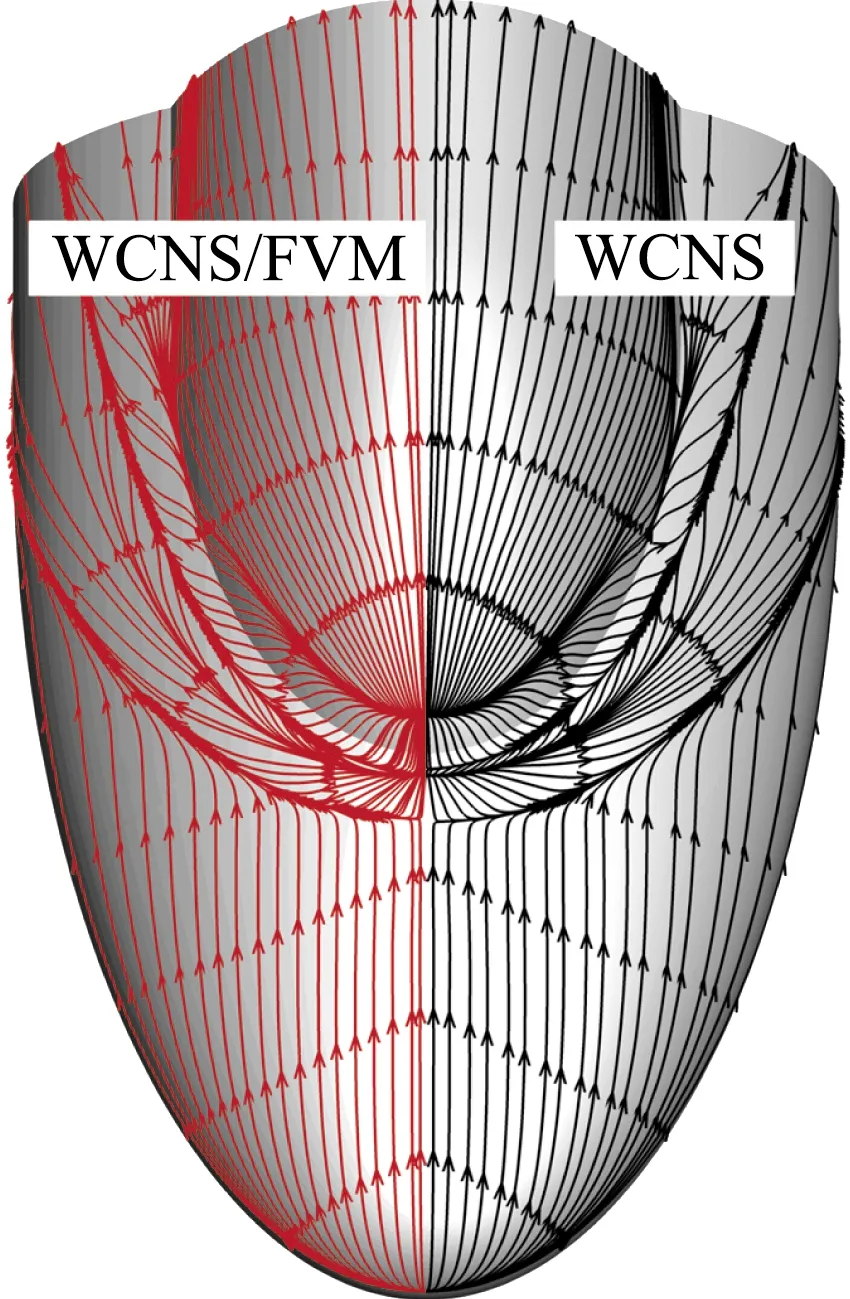
圖11 混合求解器與純高階求解器極限流線對比

從物面的壓強(qiáng)和熱流分布看(圖12)，兩種求解器計算得到的壓強(qiáng)分布與試驗數(shù)據(jù)有很好一致性，流經(jīng)第二橢圓之后，壓力與熱流均顯著上升，達(dá)到峰值。同樣地，該算例表明了，在三維情況下，混合求解器仍然能保持高精度方法的特性。

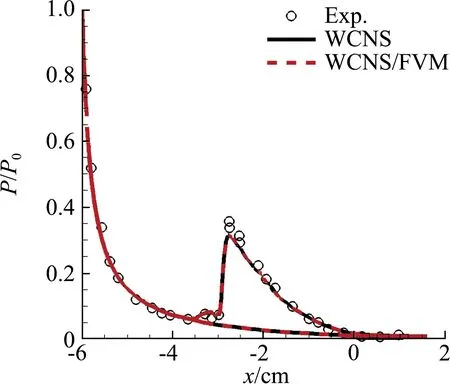
(a)對稱面壓力分布

3.3 混合求解器效率比較

之所以發(fā)展“同構(gòu)”混合求解，原因之一是其能吸收結(jié)構(gòu)求解器的高效率優(yōu)點。對上述兩個算例，對比分析了結(jié)構(gòu)、非結(jié)構(gòu)、混合求解三種策略的計算效率。對每個算例，三種策略都采用同一套結(jié)構(gòu)網(wǎng)格，非結(jié)構(gòu)求解器將其全局非結(jié)構(gòu)化計算，混合求解器將外場部分非結(jié)構(gòu)化計算。

在保證計算穩(wěn)定收斂的前提下，三種策略均采用最大CFL數(shù)。在殘差收斂曲線圖中(圖13、圖14)，迭代步代表算法效率，墻上CPU時間則反應(yīng)實際計算效率。從算法層面看(迭代步vs.殘差)，結(jié)構(gòu)求解器效率最高，混合計算次之，非結(jié)構(gòu)最慢；從實際墻上CPU時間看，規(guī)律一樣。即，兼顧了結(jié)構(gòu)網(wǎng)格的計算精度和非結(jié)構(gòu)網(wǎng)格的網(wǎng)格生成便利的混合求解策略，在計算效率上要優(yōu)于完全的非結(jié)構(gòu)網(wǎng)格計算。

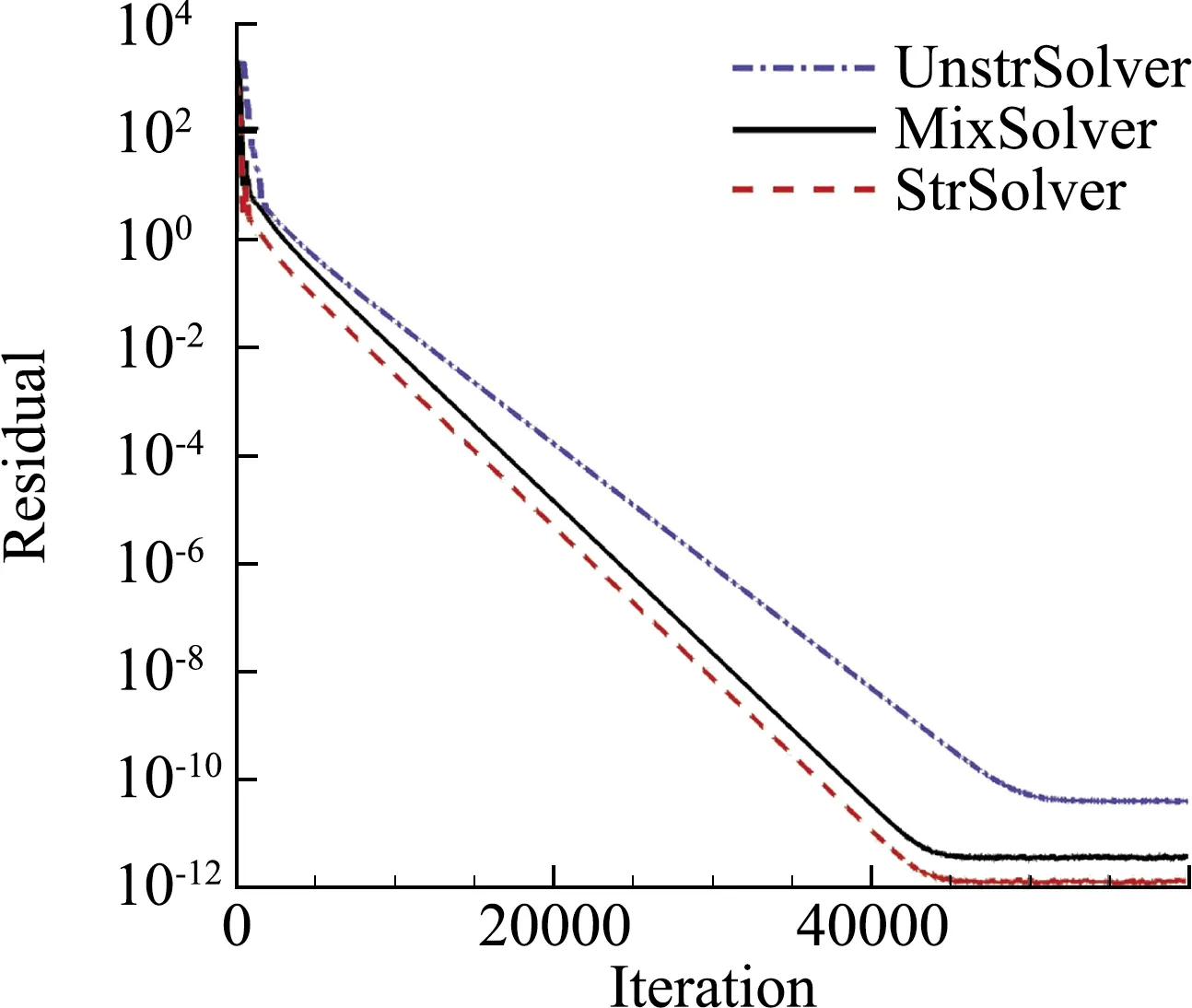
(a)殘差收斂曲線(迭代步數(shù))

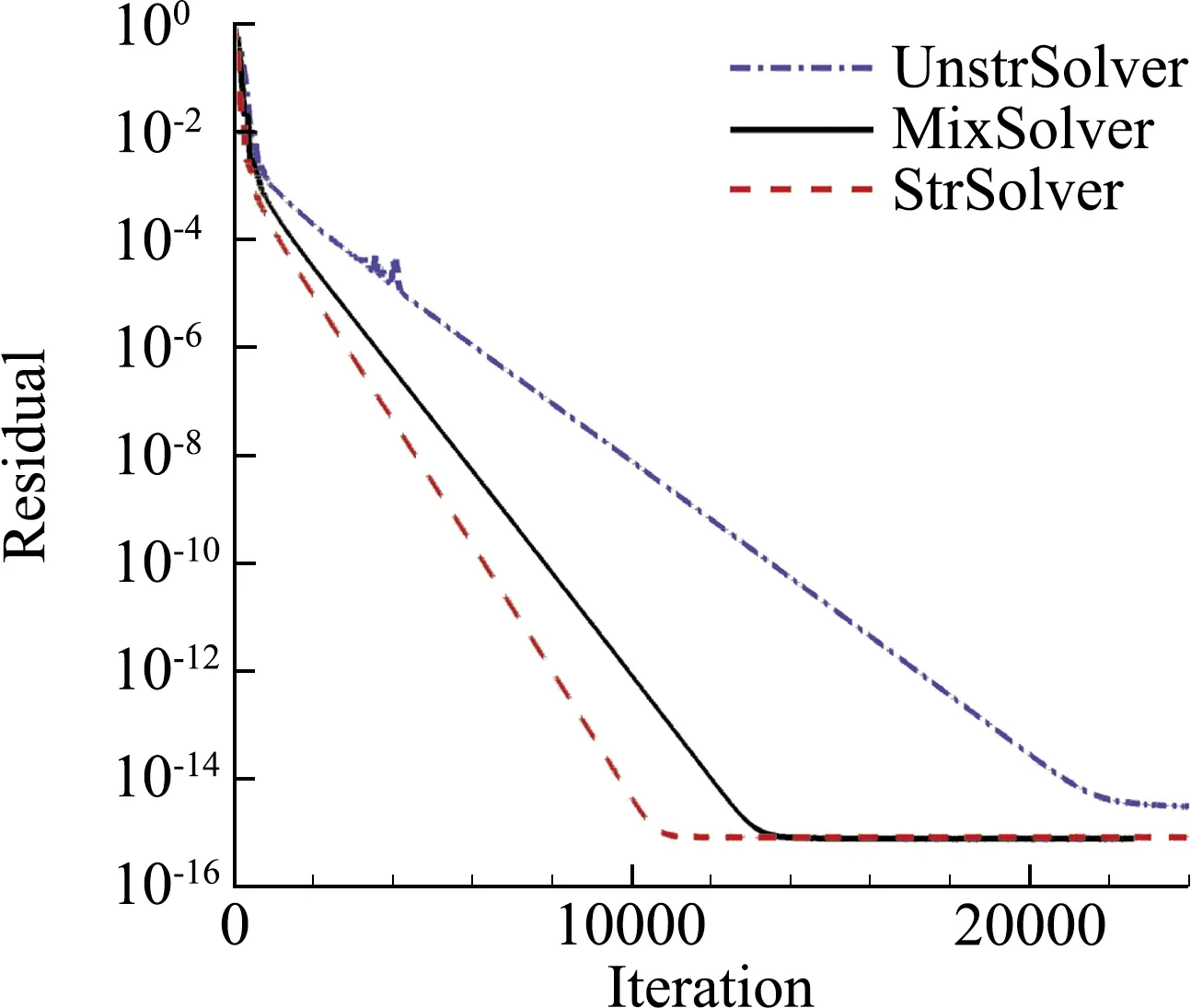
(a)殘差收斂曲線(迭代步數(shù))

4 結(jié) 論

基于風(fēng)雷軟件，設(shè)計了“同構(gòu)”混合求解策略，以及相應(yīng)的交界面抽象方法、數(shù)據(jù)結(jié)構(gòu)。作為“同構(gòu)”混合計算的應(yīng)用案例，以解決高階精度方法的工程實用化為切入點，通過在結(jié)構(gòu)網(wǎng)格上運行WCNS高階求解器，在非結(jié)構(gòu)網(wǎng)格上運行二階有限體積(FVM)求解器，以達(dá)到在流動關(guān)鍵區(qū)域高階模擬、在復(fù)雜區(qū)域非結(jié)構(gòu)方便過渡的目的。

對二維圓柱和三維雙橢球高超聲速流動問題進(jìn)行了模擬，結(jié)果表明，混合求解器能保持高階求解器的特性，驗證了風(fēng)雷軟件中區(qū)域混合計算策略的可行性，同時說明了混合計算的效率優(yōu)勢。

二階/高階混合求解的目標(biāo)，是在對流動大范圍分離、激波等典型特征處采用高階方法，當(dāng)前的工作僅是針對高超聲速流動，在高超聲速標(biāo)模外形上進(jìn)行的串行計算模擬，要實現(xiàn)在復(fù)雜外形上，高效、高精度模擬關(guān)鍵流動區(qū)域的最終目標(biāo)，必須要實現(xiàn)混合求解器的并行化。風(fēng)雷軟件中純結(jié)構(gòu)、非結(jié)構(gòu)求解器均有較強(qiáng)的并行可擴(kuò)展性[10]，但要實現(xiàn)混合求解的并行計算，必須解決結(jié)構(gòu)/非結(jié)構(gòu)網(wǎng)格分區(qū)負(fù)載平衡問題。下一步，將著力解決求解器的并行化問題，以實現(xiàn)工程實用能力，為關(guān)鍵氣動問題模擬提供技術(shù)支撐。

致謝:感謝國家數(shù)值風(fēng)洞工程軟件開發(fā)團(tuán)隊所有人員的付出和努力，感謝風(fēng)雷(PHengLEI)軟件前期開發(fā)者們的貢獻(xiàn)，也感謝工程兩委會的指導(dǎo)。