基于關聯速度的FW-H積分四極子聲源修正模型

周志騰, 王洪平, 王士召,*, 何國威

(1.中國科學院 力學研究所 非線性力學國家重點實驗室, 北京 100190; 2.中國科學院大學 工程科學學院, 北京 100049)

0 引 言

流動噪聲既是流體力學基礎研究的重要難題，又是航空工程中的重要問題。Ffowcs Williams and Hawkings(FW-H)方程[1]是目前計算流動噪聲的重要工具。隨著計算流體力學的發展，FW-H方程已被成功地應用于直升機旋翼[2-3]、增升裝置[4-5]、和飛機起落架[6]等產生的流動噪聲研究。特別是近年來，數值風洞[7]的發展更是為流動噪聲的預測提供了有力的支撐。

FW-H方程通過引入廣義函數將自由空間的Lighthill聲比擬方程推廣至有壁面的流動問題，其中的壁面(下文中稱為FW-H積分面)既可以是真實的固體邊界，也可以是流動中的虛擬邊界。FW-H方程是一個關于密度(或壓力)脈動的非齊次波動方程。遠場的噪聲可在形式上表示為流場變量和格林函數的積分(下文中稱為FW-H積分)。根據FW-H積分，遠場噪聲為單極子聲源、偶極子聲源和四極子聲源三部分貢獻的疊加。其中，與單極子聲源和偶極子聲源相關的積分分別涉及積分面上的質量通量和非定常載荷，是相關量在FW-H積分面上的面積分。與四極子聲源相關的積分是涉及Lighthill應力張量的體積分，其積分域應該包含Lighthill應力張量不為零的所有區域。計算四極子聲源相關的積分所需要的計算量和存儲量遠大于偶極子聲源和單極子聲源相關的積分。并且，常用的實驗測量和數值模擬數據難以包含Lighthill應力張量不為零的全部區域。Lighthill應力張量從FW-H積分面穿出，常會引起四極子聲源對遠場噪聲的虛假貢獻[8-9]。

在低馬赫數流動中，相對于非定常載荷對應的偶極子聲源產生的遠場噪聲，Lighthill應力張量對應的四極子聲源產生的噪聲所占比例相對較小，通常做法是忽略四極子聲源體積分項。但是，隨著來流馬赫數的增加或流動邊界的復雜化，四極子聲源的影響逐漸不可忽略[10-14]。Yao等[13]研究了來流馬赫數為0.3的半球擾流，發現回流區尾端的四極子聲源是遠場噪聲的主要來源，Tomoaki Ikeda等[10]計算了來流馬赫數為0.2、雷諾數為1×104、攻角為2°的二維NACA0012翼型繞流，結果顯示，在部分觀測點四極子聲源穿出FW-H面造成的虛假聲源與偶極子聲源的貢獻處于同一量級。

為了解決四極子積分項引起的虛假聲源問題，Shur等[15]通過在接近控制面處添加人工黏性的方法耗散Lighthill應力張量。但是，Nitzkorski等[9]認為這種方法使得被打開面的法向的輻射噪聲被低估。為了避免引入人工黏性，Wang等[11]曾在Curle積分的框架下提出了一種修正四極子聲源計算的模型。該模型利用凍結流假設將所選聲源區外的Lighthill應力張量的體積分對遠場噪聲的貢獻轉換為計算域邊界上四極子聲源流量的面積分，有效地恢復了低馬赫數翼型繞流問題中產生的四極子聲源對遠場噪聲的貢獻。Wang等[11]的工作中使用縮放的均勻來流速度作為Lighthill應力張量穿過計算域邊界的對流速度，需要將聲源區的邊界取至下游足夠遠處，以消除近場尾跡中的Lighthill應力張量對流速度的非均勻性對修正模型的影響。隨后，Nitzkorski等[9]將Wang等[11]的思路推廣至FW-H積分，并通過利用多出口面之間的交叉關聯函數構建Lighthill應力張量的通量在FW-H積分面上的對流速度，避免了依賴于經驗的縮放均勻來流作為對流速度。

上述工作在時域方法框架下修正計算四極子聲源對遠場噪聲的貢獻，有效地抑制了Lighthill應力張量穿過控制面引起的虛假聲源問題。但由于FW-H積分面的運動和對流速度的計算方式等問題，這些方法沒有被廣泛地應用在頻域方法中。Lockard等[16]提出了頻域方法框架下的四極子聲源積分項的計算模型。該模型通過連續使用分部積分，將四極子聲源的體積分近似表達為一系列面積分的和，避免了在整個計算域內存儲和計算Lighthill應力張量，并且抑制了四極子聲源體積分計算中對遠場噪聲的虛假貢獻。在這一過程中，Lockard等[16]根據Wang等[11]的工作以對流方程的形式描述Lighthill應力張量通過積分面的過程，并假設對流速度取為均勻來流的速度。該假設沒有考慮積分面上的Lighthill應力張量對流速度的非均勻性，一般難以將積分面取在近尾跡區域。

針對這一問題，本文發展一種可以在FW-H積分面上計算非均勻對流速度的模型，用于改進Lockard等[16]提出的四極子修正方法中的均勻對流速度假設。該模型受時域方法中Nitzkorski等[9]的工作的啟發，基于FW-H積分面上的關聯函數計算對流速度。與Nitzkorski等[9]的工作不同的是，我們根據Lighthill應力張量的關聯函數，而不是Lighthill應力張量的通量的關聯函數，來計算對流速度，避免了依賴于經驗選用的均勻來流作為對流速度，并考慮了對流速度空間分布的非均勻性。

本文第1部分簡要地給出FW-H方程在頻域的解，第2部分給出FW-H積分四極子聲源項修正模型以及四極子聲源項的對流速度的具體計算方法，第3部分用二維對流渦以及低馬赫數圓柱繞流兩個標準算例檢驗所發展的模型，第4部分為結論。

1 FW-H方程及其解

常用的FW-H方程的微分形式：

(1)

其中，

(2)

(3)

其中，yi=zi+Uit是隨FW-H積分面運動的坐標下的空間位置變量，Ui為無窮遠來流在yi方向的速度。不影響一般性，在本文中按照Wang等[11]和 Lockard等[16]的處理方式，取無窮遠來流僅沿y1方向，即U=(U1,0,0)。則聲源項變為

Tij=ρuiuj

(4)

式中的速度ui和uj皆為減去無窮遠來流后的速度擾動。為了將對流波動方程變化到頻域，我們根據Lockard[17]的工作定義傅里葉變換對如下：

(5)

利用式(5)，頻域中的FW-H方程可寫為：

(6)

其中k=ω/co為波數，Mi=Ui/co為馬赫數。

式(6)的解可寫為[17-18]：

(7)

其中IT、IL分別為厚度聲源與載荷聲源，分別對應于單極子聲源和偶極子聲源，表達式如下：

(8)

其中x、y分別表示觀測點與聲源所在位置。

四極子聲源積分項為：

(9)

2 FW-H積分四極子聲源項的修正

準確求解四極子聲源對遠場噪聲的貢獻需要保存FW-H積分面以外的所有Lighthill應力張量不為零的區域流場，如式(9)所示。當四極子聲源的積分域不能包含所有的Lighthill應力張量不為零的區域時，Lighthill應力張量會穿過FW-H積分面，導致四極子聲源對遠場噪聲的虛假貢獻。Lockard等[16]通過分部積分的方法將四極子體積分項(式(9))近似地表達為面積分的和：

IQ(x;ω)≈

(10)

在計算中一般取前三項。Uc為Lighthill應力張量的輸運速度，表示四極子聲源穿出FW-H積分面的速度，注意，式(10)在推導過程中假設對流速度沿流向與時間的變化可以忽略不計。Lighthill應力張量穿出FW-H積分面的過程用如下方程模化：

(11)

按照式(10)計算四極子聲源項對遠場噪聲的貢獻的關鍵是計算對流速度Uc。Lockard等[16]選取對流速度為均勻來流速度。以均勻來流為對流速度沒有考慮FW-H積分面上的對流速度的非均勻性，會導致遠場噪聲依賴于FW-H的位置。不同于Lockard的選用均勻來流為對流速度，我們采用多個出口面Lighthill應力張量的關聯函數構建對流速度，其基本思想是利用關聯函數得到四極子聲源在出口面之間的輸運時間，繼而根據出口面之間的距離得到穿出出口面的速度。與直接選用均勻來流為對流速度相比，此方法不僅提高了遠場噪聲指向性預測的準確性，而且減小了預測結果對FW-H面選取位置的依賴性。

構建對流速度Uc的 Lighthill應力張量的關聯函數為：

Rxy(τ)=

(12)

其中，Tij(y1,y2,t)與Tij(y1+Δy1,y2,t+τ)分別為上下游兩個面對應位置的信號，Δy1為所選取的兩出口面之間的距離。T為用來計算Uc的采樣時間，在文中，我們取Uc僅隨空間位置變化。如圖1所示，基于泰勒凍結假設，渦在輸運過程中不發生變形。因此，Lighthill應力張量的輸運速度Uc與渦的運動速度保持一致，并且本文考慮的渦沿方向穿過出口面，對應單元的位置僅在流向變化。需要注意的是，由于使用了泰勒凍結流假設，下游出口面的位置應取在速度梯度較小的區域[14]，并且用于求解出口速度的兩個出口面之間的距離不能太大。在3.2節的圓柱繞流算例中，第一個出口面到圓柱中心的距離大于或等于2.5D，兩個出口面的間距為 0.1D。為了便于計算，本文用于計算出口速度的兩個出口面都垂直于流向。式(12)的離散形式寫為：

圖1 四極子聲源修正模型的求解示意圖

Tij(y1+Δy1,y2,iΔ′+jΔ′)

(13)

Uc=Δy1/τr

(14)

3 結果與討論

3.1 二維對流渦

二維對流渦為可壓縮歐拉方程的一個精確解，是檢驗FW-H積分修正方法的正確性的典型算例[16,20-21]。在圖2和圖3所示的對流渦算例中，渦以勻速直線運動沿y1方向向下游運動，嚴格滿足凍結流假設。壓力與速度場的表達式為:

圖2 初始時刻二維對流渦壓力分布云圖

圖3 無量綱時刻t=25時二維對流渦壓力分布云圖

u=M-a0a1y2exp((1-r2)/2)

v=a0a1(y1-Mt)exp((1-r2)/2)

(15)

其中，po為無窮遠處的壓力；γ為空氣的熱容比,取1.4；y1、y2表示二維笛卡爾坐標系；M為對流馬赫數；t為時間。

(16)

式(15)式(16)所有的量皆經過無量綱化，參考物理量為單位長度L、聲速co以及密度ρ。Lighthill應力張量滿足：

(17)

不失一般性，我們在計算中將FW-H積分面取為矩形，其在y1、y2方向的取值范圍分別為[-5L,5L]、[-5L,5L]，如圖3所示。當來流馬赫數為0.2時，在無量綱時刻t=25，僅有一部分四極子聲源在FW-H積分面內，穿出下游出口面的四極子聲源使常規的FW-H積分的計算結果產生誤差。我們采用式(10)和式(14)修正了Lighthill應力張量穿出FW-H積分面所引起的誤差，如圖4所示。需要注意的是，圖中的黑色實線表示FW-H方程所計算出的(IT+IL)的相反數。由于觀察點的真實壓力脈動趨于0，則不進行修正的FW-H方程的解實際上遠遠高估了壓力脈動的大小，因此誤差近似為此解的相反數，四極子聲源修正模型所得結果應逼近于此誤差。在計算式(10)的過程中，我們取了不同的n值，當n=3時(與Lockard等[16]所取的n值相同)，我們的方法在二維渦的上下游遠場觀測點均能夠修正Lighthill應力張量穿出FW-H積分面引起的誤差。這一結論證實了我們的模型在二維對流渦運動中的有效性。

(a)Observer(-100,0)

3.2 二維圓柱繞流遠場噪聲

低雷諾數圓柱繞流的遠場輻射噪聲是一個廣泛應用的檢驗流動噪聲計算模型和方法的算例。直接數值模擬[22]、FW-H方程[9]以及精確格林函數[23]等方法皆被應用于此問題當中，并且相應的結果顯示出一致性。其中，Inoue等[22]較早地利用直接數值模擬的手段系統研究了雷諾數150下，二維圓柱繞流輻射噪聲的指向性、遠場衰減特性以及遠場壓力脈動關于馬赫數的標度率，并常被用作比對算例。本文的結果將與Inoue 等[22]的直接數值模擬結果進行比較，以檢驗所發展的模型的有效性。

我們通過數值求解不可壓流動的Navier-Stokes方程作為遠場噪聲的聲源。聲源數值模擬的設置如圖5所示，圓柱中心在原點，直徑為D，來流速度為U0，基于來流速度與圓柱直徑定義的雷諾數為150，坐標軸y1、y2分別對應流向與垂向。流場計算采用浸入邊界方法，計算區域為[-10D,15D]，[-12D,12D]，均勻網格的尺度為0.01D，流場計算的時間步長為0.001D/U0。FW-H積分面選為長方形，上游以及兩側的面位置分別為y1=-D與y2=±2D，計算聲場的采樣步長為0.027D/U0。為了檢驗結果對出口面位置的敏感度，我們選取了不同位置的出口面，分別為y1=4.5D、y1=2.5D，計算了馬赫數為0.2下，位于(0D,100D)處觀測點的壓力脈動，并與Inoue 等[22]的直接數值模擬結果進行了對比。結果如圖6所示，其中Tp為所選觀察點處壓力脈動的周期，對于不同位置的出口面，我們的模型均能夠消除四極子聲源穿出FW-H積分面引起的誤差，與直接數值模擬的結果相符。此結果表明我們的模型不依賴于出口面位置的選取。

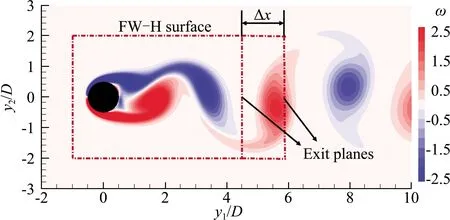
圖5 二維圓柱繞流渦量分布云圖與遠場噪聲計算所用FW-H面的位置示意圖

圖6 馬赫數0.2下，不同位置的出口面得到的(0D,100D)處觀測點的壓力脈動，并與Inoue的直接數值模擬結果對比

圖7比較了利用各種方法得到的遠場壓力脈動的指向性，|Δp|為壓力脈動幅值的均方根。參考Inoue 等[22]對觀測點位置的選取，圖7中的觀測點到圓柱中心的距離定義為75[1+Mcos(θ)]D，其中M為來流馬赫數，此處為M=0.2，方向角θ為觀測點位置對應向量與y1軸正向的夾角。圖中的黑色實線為Inoue 等[22]的直接數值模擬的結果。紅色點劃線為利用本文所發展的模型的計算結果，藍色雙點劃線為四極子聲源對流速度取為來流速度的結果，紫色虛線為未經FW-H積分四極子聲源修正的結果。在本文所選用的FW-H積分面下，如果在用FW-H方程計算遠場噪聲中不考慮四極子聲源修正，將會引起指向性和壓力脈動幅值嚴重偏離DNS值。如表1所示，在本文坐標系下，Inoue等[22]給出的最大壓力脈動在101.5°，未經修正的結果在120.0°，經均勻來流為對流速度的四極子聲源修正后，最大壓力脈動在92.0°處，可經本文所發展的方法修正后，最大壓力脈動在100.0°，指向性的最大誤差降至2°以下。在壓力脈動幅值誤差明顯的120°方向角處，未經修正的幅值的誤差為31%，經均勻來流為對流速度的四極子聲源修正后，誤差為12%，可經本文所發展的方法修正后，誤差則降為4%以下。這一結果表明了本文所提出的四極子聲源修正模型的有效性，并且本文所提出的模型改進了Lockard等[16]所提出的頻域FW-H積分修正方法。

圖7 二維圓柱繞流中，利用各種方法計算出的遠場壓力脈動指向性

表1 最大壓力脈動方向

4 結 論

針對FW-H積分中的四極子聲源項常在遠場噪聲的計算中引起虛假聲源的問題，本文在頻域方法的框架下改進了四極子聲源項的修正模型，用于修正Lighthill應力張量穿過積分域邊界引起的誤差。該工作基于泰勒凍結流假設模化Lighthill應力張量穿過積分域邊界的過程，特色是基于關聯函數計算Lighthill應力張量的對流速度，而不是將對流速度取為均勻來流。所提出的模型考慮了對流速度的空間非均勻性，改善了非均勻流動區域FW-H積分面對遠場噪聲的影響。利用二維對流渦算例以及低雷諾數圓柱繞流算例檢驗了所提出的模型，結果表明模型準確修正了四極子聲源穿出FW-H積分面所導致的遠場噪聲計算誤差。作為在頻域方法中考慮FW-H積分面上的非均勻對流速度的第一步工作，我們在二維流動的例子中驗證了基于關聯函數構建Lighthill應力張量的可行性，并將進一步把該模型用于三維流動的四極子聲源的修正。