增強優化格式在聲散射問題中的應用

武從海, 馬瑞軒,2, 王益民, 張樹海,*

(1.中國空氣動力研究與發展中心 空氣動力學國家重點實驗室, 綿陽 621000；2.中國空氣動力研究與發展中心 氣動噪聲控制重點實驗室, 綿陽 621000)

0 引 言

氣動聲學問題通常要求數值格式具有良好的多尺度分辨率。高精度緊致差分格式由于其良好的譜分辨率，在計算氣動聲學中得到了廣泛應用[2-3]。但是緊致格式在使用時一般需要求解全局方程組，這會導致計算效率的降低和并行處理上的困難。

優化差分格式是另一類常用于氣動聲學問題的數值格式[4]。優化差分格式分為中心型和迎風型兩種。中心型格式不含耗散，在實際應用中需要增加濾波過程。而迎風型優化格式由于其內在的耗散一般無需濾波。Tam認為迎風型優化格式通常會存在一定程度的不穩定性[5]。文獻[6]給出了一種穩定性判據，發現了兩種迎風型優化格式存在不穩定性，并采用這個判據作為約束條件分別構造了相應的穩定優化格式。但是，構造迎風優化格式首先需要設計一個綜合考慮耗散誤差與色散誤差的目標函數，而該目標函數的設計存在較大的經驗性成分。

優化格式通過犧牲收斂精度的階數而對某一特定范圍波數的波形(比如短波)的分辨率進行優化[4]。但是損失的精度階數會導致格式在波數0附近的波數誤差增大，因而格式在含大量低頻成分波形的遠距離傳播問題中表現不佳。文獻[1]中，通過將優化格式和最高階格式加權組合，得到的格式達到了最優階收斂精度，并且對于無量綱波數不大于π/3的單色波的波數誤差幾乎為0。

由于該格式相比普通優化格式具有更好的譜分辨率性質，這里稱其為增強優化差分格式(下文簡寫為增強優化格式)。增強優化格式由優化格式和最高階格式非線性加權組合得到。本文將基于不同的線性優化格式構造增強優化格式，并通過線性傳播方程的數值測試選取表現較優的格式，最后針對聲散射問題進行數值模擬與分析。

1 增強優化格式

1.1 差分格式的波數誤差

本文討論的格式均為中心格式，采用的模板為7點對稱等距模板，網格間距為h。這種差分格式可寫為:

(1)

中心格式的系數滿足反對稱條件，即:

a0=0，a1=-a-1，a2=-a-2，a3=-a-3

對于波數為k的單色波,

f=eikx

其導函數

f′=ikf(x)

對于格式(1)，我們可以在節點處得到類似的公式:

(2)

考慮光滑函數f(x)，其傅立葉變換為:

F(f(x))=F(k)

則

F(f′(x))=ikF(k)

(3)

(4)

根據泰勒展開，差分格式的截斷誤差為:

=Mf(q+1)(x)hq+O(f(q+2)(x)hq+1)

(5)

其中M是由差分格式決定的常數。對上式做傅立葉變換得:

M(ik)q+1F(k)hq+O(kq+2hq+1)

(6)

(7)

由該式可知，高階精度的格式在波數0附近的波數誤差更小。

1.2 線性優化差分格式

本小節討論7點對稱模板上的最高階格式及優化格式。在該模板上的最高階顯式差分格式為六階。根據泰勒展開，六階格式的系數(用上標S表示)需滿足:

(8)

求解得到的結果為:

(9)

這里考慮的優化格式為四階精度的中心格式，且滿足在某無量綱波數為κ0∈[0,π]時波數誤差為0。根據泰勒展開和有效波數的計算公式可得到系數(用上標O表示)滿足的方程組:

(10)

文獻[5]中的七點色散關系保持(Dispersion Relation Preserving,DRP)格式可由κ0取1.42151084298得到，下文用DRP4表示。文獻[1]中的優化格式為無量綱波數κ0取π/3時的情況，對應單位波長所含網格點數(Points Per Wavelength, PPW)[8]PPW=6。六階中心格式Cen6也可視為κ0趨于0的極限情況。

(11)

Opt2的系數為:

(12)

Opt3的系數為:

(13)

(a)Modified wavenumbers

1.3 增強優化差分格式

根據下文中該格式的設計，其波數誤差在[0,κ0]中非常小，而對于更高波數的單色波，其表現與普通的優化格式無異。而對于更一般的波形，如果將波形的每一小段(如四個節點)當作單色波，由于相位誤差小，各段的波形應可以得到較好的保持，那么整體波形理應可以得到保持。而實際的波形中，由于一些非常高波數成分的存在，這使得該格式的表現不如在單色波中突出。

構造增強優化格式時，首先仿照文獻[9]給出一種局部波數指示子：

IWj=[(fj-2-4fj-1+6fj-4fj+1+fj+2)2+

(-fj-2+2fj-1-2fj+1+fj+2)2]/

[(fj-1-2fj+fj+1)2+(-fj-1+fj+1)2+ε]

(14)

ε是一個小的正數，用來防止分母為0，這里取1×10-40。那么對于單色波f=sin(kx+φ)+C(C為常數項)，

(15)

其中κ=kh為無量綱波數。

對于如何由IWj構造單色波相位誤差較小的權值，最直接的方法是先求解無量綱波數κ，再構造權系數。令:

(16)

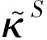
從IWj得到λ0的過程需要計算反三角函數和幾個三角函數，計算量相對較大。因此采用一個簡單的公式來逼近：

λj=min(1,γj)

(17)

這里min表示兩者的較小值，其中

(18)

則λj在0到1之間，這使得增強優化格式為兩個子格式的凸組合。

并且,

λj=aκ2+O(κ4)

其中系數C6和C4可由泰勒展開計算得到。

根據截斷誤差與波數誤差之間的關系式(7)，兩個子格式的波數誤差為：

那么增強優化格式的波數誤差為：

=-C6(1-λj)κ7+C4λjκ5+O(κ9)

=(aC4-C6)κ7+O(κ9)

為了減小波數誤差，令首項系數為0，則:

(19)

對于參數b，我們要求當無量綱波數為κ0時γj為1。那么:

則:

(20)

本文構造的增強優化格式為：

(21)

表1 幾種優化格式對應的參數a和b的值

圖2給出了幾種格式在0≤κ≤3π/4之間波數誤差的絕對值，橫坐標為無量綱波數，間隔π/60，縱坐標采用對數坐標。其中Com6表示6階中心緊致格式[2]。從圖2中可以看出，在波數0附近DRP格式由于只有四階精度因而誤差最大，其次是Cen6，再次是Com6，而幾種增強優化格式的誤差較小。在優化格式及增強優化格式各自的κ0處，根據其設計原理，波數誤差為機器0。而DRP和EOT由于相應的κ0不在采樣點上，圖中該處僅出現小幅下探。對于幾種增強優化格式，隨著相應κ0的變大，格式在無量綱波數較小時的誤差隨之變大，而在無量綱波數較大時誤差則會變小。

注意上述波數誤差的結果是基于單色波得到的。對于更一般的波形，其各單色波成分的波數誤差與圖2所示并不一致。

圖2 幾個格式波數誤差絕對值的比較

2 收斂精度驗證

文獻[1]中已經對增強優化格式的收斂精度進行了分析，其結論對于本文中幾種增強優化格式依然成立。增強優化格式在流場光滑區域基本為6階精度，但是由于格式的非線性性質，其收斂精度可能會在極值點附近降低。具體為：若求解問題是光滑的，且極值點處二階導數不為0，則增強優化格式除極值點附近為5階外均為6階，則L1收斂精度為6階，L∞收斂精度為5階；若極值點處二階導數為0，則增強優化格式L1收斂精度為5階，L∞收斂精度為4階。

下面通過數值實驗驗證收斂精度。考慮如下線性對流方程的初值問題：

(22)

表2 增強優化格式收斂精度測試

3 一維算例對比測試

本節通過一維算例來測試對比幾種增強優化格式，同時參與計算的還有六階中心格式Cen6、優化格式DRP4及六階中心緊致格式Com6。時間格式采用三階TVD龍格庫塔方法[10]。在實際計算中常常采用低耗散低色散龍格庫塔方法[11-12]。

3.1 正弦波傳播問題

采用對流方程進行測試，對流速度設為1，其方程為：

ut+ux=0

(23)

初值為u0(x)=sin(4πx)，求解區域為[0,1]，計算的CFL數均取0.1，PPW分別取6和12，推進的時間分別為T=20和1000。圖3中給出了[0,0.5]間的計算結果。兩種情況下，六階中心格式Cen6和優化格式DRP4的誤差都較大。當PPW為6時，其它格式除EO3之外均得到了較好的結果，相比而言，EO2更為準確。這是由于EO3僅對無量綱波數在[0,π/4]的單波誤差很小，PPW=6的正弦波的無量綱波數為π/3，超出了此范圍，從圖2中也可以看出此時EO3的波數誤差較大。當正弦波的PPW為12時，四種增強優化格式及緊致格式均取得了較好的結果。

(a)PPW=6, T=20

兩種情況下，EOT的結果大幅均優于其組成成分格式DRP4。實際上，從圖2的結果可以看出，二者的波數誤差相差至少一個量級。這也說明了增強優化格式在單色波問題中有著上佳的表現。

3.2 高斯波傳播問題

這里計算一個高斯波的傳播問題[13]，其控制方程與前一問題一致，而初始波形為：

(24)

其中h=1為空間步長，取時間步長Δt=0.4。計算終止時間為T=400和1000, 計算結果顯示在圖4中。整體而言，除優化格式DRP4外，幾種格式均獲得了較好的結果，其中六階緊致格式Com6的結果最接近精確解。優化格式DRP4在波后發生了較明顯的數值波動，這是由于這些波動的成分對應的相速度偏大所致。圖4(b)中局部的放大圖中可以看到六階中心格式Cen6存在相對明顯的數值波動，與DRP4格式相反，其原因為相應成分的相速度偏小。四種增強優化格式中，其結果最好的是EO3，然后依次是EO2、EOT和EO1，其中EOT和EO1偏離精確解較大。這是由于該高斯波在步長為1時主要由長波(波數較小)構成，而此時這兩種格式有一定的過度優化，導致對PPW較大的波數誤差相對較大。

(a)T=400, Δt=0.4

圖4(c)給出了時間步長取Δt=0.1時T=1000的計算結果。相比圖4(b)，計算結果在高斯波兩端的振蕩幅度明顯加大。這說明當Δt=0.4時，時間格式的耗散較大，消除了部分振蕩。該算例中，EO2和EO3取得了相對較好的結果。由于中心格式沒有耗散，實際計算中通常采用濾波方法[2,14]來消除這種連續流場中的非物理振蕩。

4 聲散射問題數值研究

當聲波穿過旋渦時，會發生強烈的非線性散射現象，聲波的幅值和相位都會發生顯著的變化[15]。下面采用增強優化差分格式及其他常用的氣動聲學計算格式直接數值求解二維歐拉方程，計算平面聲波穿過等熵渦的散射問題。

以無窮遠處聲速和密度對問題進行無量綱化。背景流動中二維等熵泰勒渦的渦心位于計算區域的中心(0,0)，其流動參數如下[16]：

uθ=Mvrexp[(1-r2)/2]

(25)

ur=0

(26)

(27)

(28)

其中，uθ為背景流動切向速度，ur為徑向速度，ρ和p分別為密度和壓強。最大馬赫數Mv=0.125，γ為氣體絕熱指數(空氣中一般取為1.4)。

如圖5所示，計算區域為[-20,20]×[-20,20]。左邊界入射平面波形式為：

圖5 平面聲波穿過泰勒渦示意圖

(29)

其中，ρ′、u′、v′、p′分別為入射聲波的密度、x方向速度、y方向速度、壓強。聲壓振幅ε=1×10-5，波長λ分別為0.8和1。在計算區域右側和上下兩邊設置吸收層，減小反射聲波對計算的影響，滿足無反射邊界條件，具體形式參見文獻[17-18]。

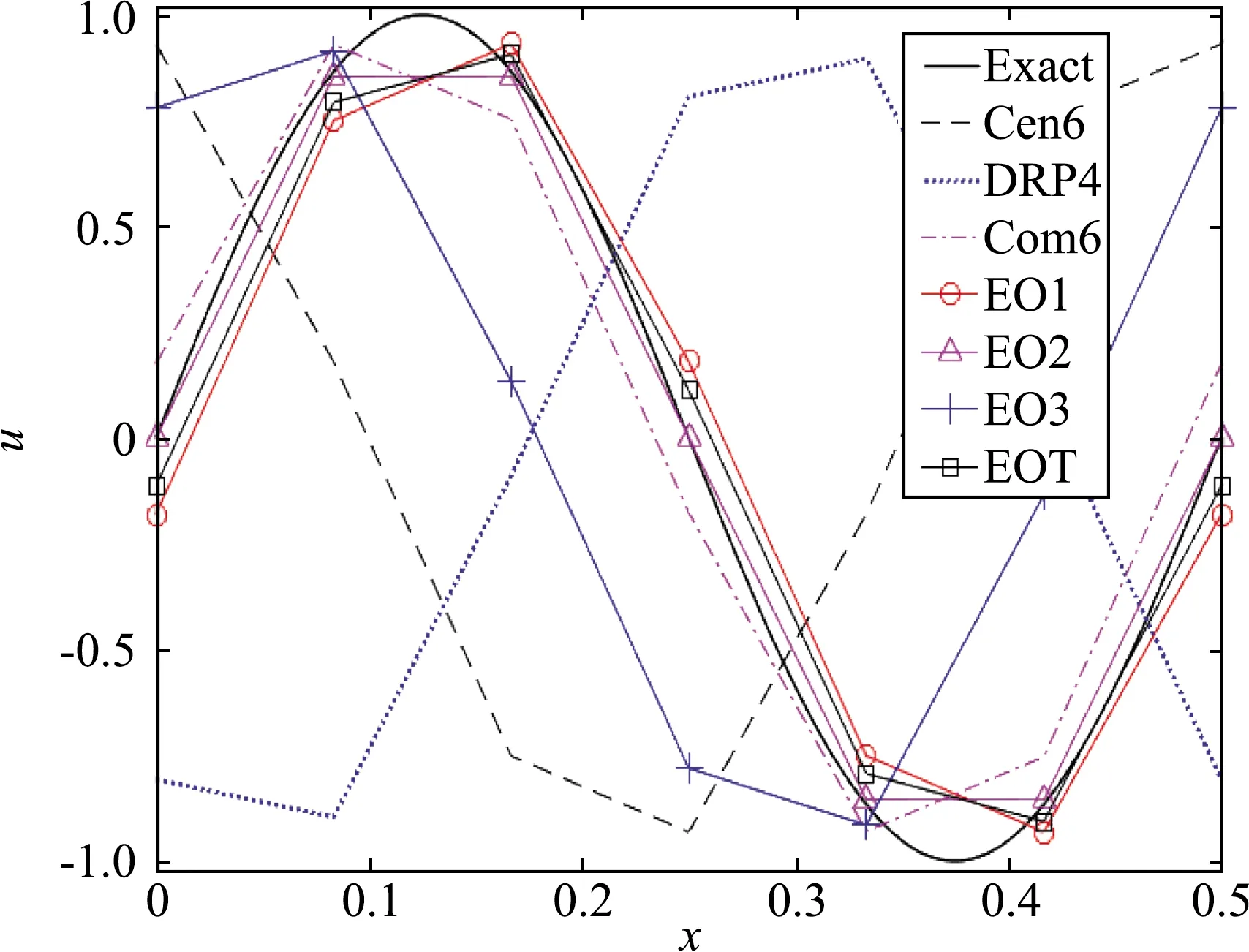
根據一維算例的結果，我們采用綜合表現最好的EO2格式計算此問題。為了進行比較，同時還采用了六階中心格式Cen6、優化格式DRP4以及六階緊致格式Com6進行計算。為了便于比較，計算中統一采用了8階緊致濾波格式[2]進行濾波。由于該問題沒有理論精確解，這里采用時間步長為0.004，空間步長為0.02的六階緊致格式計算結果作為該問題的參考精確解(圖中用Ref.表示)。λ取0.8和1時計算終止時間分別取t=56和60。圖6給出了λ=1、t=60時參考精確解的聲壓分布。可以看到聲波穿過旋渦后會發生明顯的畸變。在旋渦正后方有明顯的相移，聲波幅值快速衰減，在局部形成“寂靜區”。下游±15°的方向形成兩條一級強噪聲干擾條帶，在一級條帶外側，形成若干個次級噪聲干擾條帶，強度依次減弱。由于泰勒渦逆時針旋轉，干擾條帶關于y軸不對稱，且旋渦上方干擾強度大于下方。

圖6 λ=1、t=60時聲壓云圖

該問題計算時間步長和空間步長分別取0.02和0.1。圖7給出了r=10的圓周上散射聲壓的指向性分布。首先我們取入射波波長為0.8。圖7(a)為幾種格式在各個方向的散射聲壓均方根。從圖7(a)中可以看出，在這種相對較粗的網格下，數值結果相比參考解有較明顯的誤差。其中增強優化格式EO2與緊致格式Com6的結果相差很小，它們與參考解之間的差距較小。在聲波散射的主要區域，其幅值與參考解基本符合，在25°到70°之間，其幅值隨角度變化有一定幅度的振蕩。聲波散射影響較小的區域，其結果的幅值誤差略微偏大。六階中心格式的誤差較大，而優化格式DRP4表現最差。然后我們將入射波波長設為1，圖7(b)給出了計算結果散射聲壓均方根的指向性分布。結果與圖7(a)相似，但是誤差變得更小了。說明對于該問題，隨著入射波的波長的增加，數值計算更容易獲得好的結果。

(a)λ=0.8

5 時間效率討論

本文數值模擬均采用Fortran程序在CPU為Intel Core i7 6700K@4GHz的臺式機上單線程計算。編譯優化選項為“-O2”。

對于3.2節中高斯波傳播問題Δt=0.1、T=1000的情況，即圖4(c)對應的算例，我們記錄了幾種格式該算例的計算時間。然后將空間間距兩次減半，分別記錄了其計算時間，三次計算的時間均列入表3中。從表3中可以看出增強優化格式EO2僅需緊致格式Com6不到一半的時間。

表3 幾種格式計算高斯波傳播問題所需時間(Δt=0.1, T=1000, 單位: s)

表4中給出了聲散射問題幾種格式的計算時間。從表4中可以看出增強優化格式EO2所需時間少于緊致格式Com6，但是該算例中EO2取得了與緊致格式相近的結果。并且，EO2是顯式格式，相比緊致格式更容易處理邊界條件并且更適于并行計算。

表4 幾種格式計算聲波散射問題所需時間(單位：s)

6 結 論

增強優化格式為最高階格式與線性優化格式的加權平均。加權系數通過極小化單色波的相位誤差得到，加權的過程保證了格式的最優階收斂精度，并且提高了分辨率。該類格式對于單色波問題的誤差很小，而對于其它連續波形的傳播問題，也有較好表現。

本文給出了七點增強優化格式的統一構造方法，并比較了幾種增強優化格式。線性傳播問題的數值實驗表明增強優化格式EO2綜合表現相對較好。針對平面聲波穿過泰勒渦的散射問題，采用了增強優化格式EO2進行數值模擬，并比較了幾種不同類型的格式。結果表明增強優化格式EO2的結果與六階中心緊致格式相近，但是需要的計算時間更少。另外，由于該格式為顯式格式，因此相比緊致格式更容易處理邊界條件，并且更適于并行計算。

下一步將采用更多算例對該格式進行進一步測試，并將相應算法加入國家數值風洞(NNW)工程擬開發的氣動噪聲數值模擬軟件。NNW工程是我國在2018年底啟動的項目，旨在自主研發功能先進、種類齊全的CFD軟件系統，相關介紹及詳細進展參見文獻[19]。