面向新工科，物理化學教學邏輯思維能力培養探索

李廣利 劉軍 賀全國

摘? 要：邏輯思維能力培養是新工科背景下教學改革的重要方向。文章探討了物理化學教學中培養學生邏輯思維能力的基本方法有：巧妙運用形式邏輯和高數思維，靈活運用邏輯結構圖，適時穿插邏輯思維方式。教學實踐表明，該嘗試不僅促進了學生對物理化學知識的理解和掌握，而且強化了學生的邏輯思維能力訓練和培養。

關鍵詞：新工科;邏輯思維能力;物理化學;教學改革

中圖分類號：G642? ? ? ?文獻標志碼：A? ? ? ? ?文章編號：2096-000X（2020）34-0020-05

Abstract： Improving logical thinking ability is an important issue of teaching reform towards emerging engineering education. Based on research of teaching practice， the approaches for training ability of logical thinking include skillful application of the formal logic and advanced mathematical thinking， flexible application of logical structure diagram， and appropriate introduction of logical thinking mode. The teaching experience have showed that the attempt not only makes it easier for students to understand and master the relevant knowledge， but also improves their logical thinking ability significantly.

Keywords： emerging engineering education; logical thinking; Physical Chemistry; teaching reform

為推動我國工程教育改革創新，教育部2017年正式啟動高校新工科建設項目，“復旦共識”和“天大行動”等新工科建設重要文件相繼發布。高校新工科建設旨在培養復合型、善于跨界整合、且富有創新創業精神的新工科人才，打造新經濟發展的強大智力引擎以助推我國經濟高質量發展。邏輯思維是大腦思維的一種高級形式，它幫助人們清楚地認識客觀事物的本質特征和規律性聯系。邏輯思維能力也是新型工程技術人才的思維武器，在創新創業和跨界整合等實踐活動中發揮著“指南針”作用。因此，培養理工科學生的邏輯思維是新工科建設的一項重要內容。

然而，近年來高等教育功利化現象比較普遍，很多高校人才培養只重視專業技能訓練而忽略邏輯思維能力的培養。很多大學生“唯分是求”“唯利是圖”，以拿到學分和就業為目的，只重視與就業直接相關的專業技術訓練，放棄了邏輯思維能力等高層次能力的追求。這種人才培養方式已帶來諸多弊端，如畢業生就業面窄，自主學習能力差，缺乏創新能力和跨界能力。高校應以新工科為導向，加強邏輯思維能力培養，實現專業技能訓練和邏輯思維能力培養“雙管齊下”。因此，如何加強邏輯思維能力培養是值得深入探討的教育問題。

邏輯思維是指借助于概念、判斷、推理等思維形式能動地反映客觀現實的理性認識，是人們認識客觀事物的一種基本思維方式。邏輯思維主要以抽象的概念、推理和判斷為思維的基本形式，借助演繹、歸納、綜合、分析、比較、抽象和具體化等思維方法，揭示事物的本質屬性和客觀規律。作為一門重要的化工專業基礎課程，物理化學概念抽象復雜且涉及紛繁復雜的公式推導，因此很多學生課堂上一頭霧水，難以消化和理解。同時它又蘊含著豐富的邏輯思維方式，歸納與演繹、類比、假說與模型化等邏輯思維方式展現得淋漓盡致。本文面向新工科，緊密結合物理化學的課程特點，主要探索物理化學教學中培養學生邏輯思維能力的基本方法。

一、 巧妙運用形式邏輯，培養邏輯思維能力

物理化學的概念和命題具有很強的邏輯性，如對內部邏輯把握不到位，就容易出現概念混淆和認識誤區。例如作者在教學實踐中發現，大多數學生對化學平衡認識存在誤區。學生會想當然地用正逆反應速率相等來判斷化學反應平衡的達成。實際上化學平衡屬于熱力學范疇，是不需考慮時間變量。顯然，采用具有時間變量的動力學體系研究處理無時間變量的熱力學體系是錯誤的。很多學生受一些無機化學教材的影響，誤將平衡常數大小用于判斷反應是否可逆。實際上他們預先假設所有的反應都是可逆反應，進而以平衡常數作為標準來批判反應是否可逆。從形式邏輯上來看，不可逆和可逆化學反應互為矛盾關系，二者的外延之和即構成化學反應的外延。假設所有的化學反應都是不可逆反應，那么可逆化學反應就不存在了，即不可逆化學反應就和化學反應為全同關系、外延重合，這顯然有悖于形式邏輯。實際上，平衡常數大小只能用于判斷反應的完全程度，而與化學反應的方向無關。化學反應的可逆與否涉及到反應的方向性問題，故不能用平衡常數大小加以判斷。通過巧妙運用形式邏輯，能幫助學生走出認識誤區，提高邏輯判斷能力。

巧妙運用形式邏輯知識，還可幫助學生梳理物理化學重要命題的證明思路，提升學生對物化重要命題的邏輯判斷能力。例如，熱力學第二定律兩種表達方式的等效性證明就可參考形式邏輯思維方式。可以采用反證法和直接證明逆否命題法兩種方法。顧名思義，反證法就是通過證明反論題假，間接證明正論題的方法。證明方法關鍵要建立反證法的形式邏輯結構，具體包括以下步驟：1. 明確所要證明的命題（即論題）;2. 證明該命題的證據（即證明論據）;3. 由于已知的論據無法直接證明論題，故可從反面入手，設立相應的反論題，運用論據證明反論題假，從而依據排中律證明正論題真。直接證明逆否命題法則是根據正命題（若A則B）及其逆否命題（若非B則非A）之間的等價關系，通過直接證明逆否命題真，從而推斷其正命題真。通過適當穿插形式邏輯知識，幫助學生打開思路，然后以熱力學第二定律等效證明為例引導學生自行證明，通過練習加以強化，提高學生的邏輯判斷能力和邏輯思維能力。

二、巧妙借用高數思維，提高邏輯推理能力

物理化學主要借助大量的數學推導和邏輯推理以研究化學的基本原理和普遍規律。物理化學教材編排和課堂教學一般采用以下思路：首先從物理化學的基本概念、基本原理和基本假設出發，通過層層嚴密的邏輯推理，最終得到反映物化基本規律的數學表達式。由于邏輯推理過程具有嚴密性，因此得到的結論（公式、數學表達式等）往往具有一定的適用條件，這無疑增大了物理化學學習的難度。因此，在物化教學中，要積極引導學生動手推導，強化學生數學推導技能和邏輯推理能力。如在熱力學教學時，只要求學生記住最基本的dU=TdS-pdV，提示學生結合熱力學函數H、G、A的定義，自行推導其他3個熱力學基本關系式：dH=-SdT-pdV;dG=-SdT+Vdp;dA=-SdT-pdV。繼續推導就可以得到熱力學系數關系式和Maxwell關系式。這樣不僅有效避免了死記硬背，還培養了學生的邏輯思維能力。

此外，物理化學很多公式推導過程涉及大量的高數知識（主要是微積分、全微分、偏導數）。教學過程應巧妙借用這些高數思維，幫助學生更好地理解物化概念。例如，講述狀態函數概念時，可借用高等數學語言幫助學生理解。狀態函數的變化值只與始末狀態變化有關，而與變化途徑無關，即狀態函數的變化在數學上是嚴格的定積分。狀態函數在高數上具有全微分性質，也就是說狀態函數微小變化是熱力學函數的全微分。又如，講述偏摩爾量時，強調從數學中全微分和偏微分的概念進行理解。另外，化學勢教學時也可以引導學生運用高數思維進行思考，化學勢與溫度和壓強的關系實際上就是求化學勢對溫度或壓強的一階偏微分。

三、靈活運用邏輯結構圖，建立知識邏輯體系

美國著名教育心理學家J.S.布魯納高度重視學習材料本身的內在邏輯結構，他認為學習變化的本質是將內在邏輯結構的教材與學生原有的認知結構聯系起來，使新舊知識發生相互作用。物理化學是由基本概念、基本原理和基本研究方法等相互交織而成的邏輯網絡。教學時，可以靈活運用邏輯結構圖，打破教材的邏輯結構的局限，幫助學生構建知識點之間相互邏輯聯系，引導學生從內在邏輯結構層面理解和掌握物化知識，從整體層面把握物理化學。

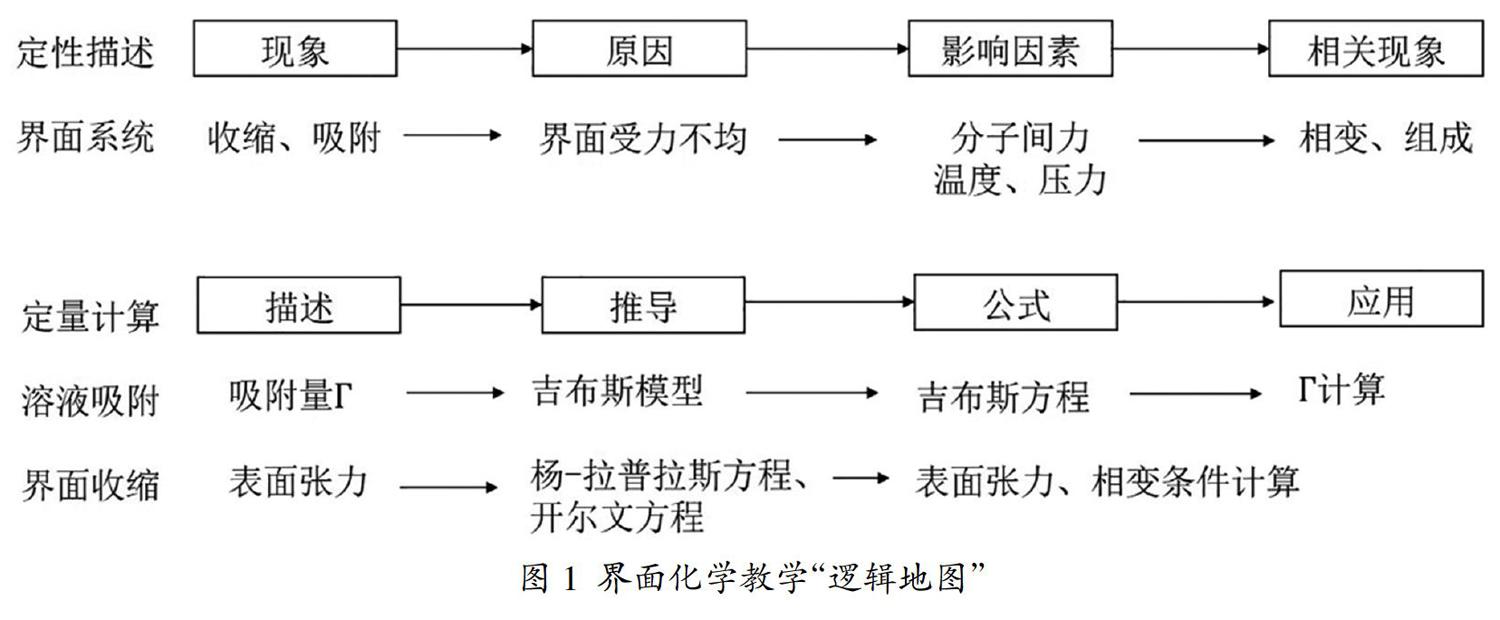
在講授物理化學知識前，首先向學生展示“邏輯地圖”（如圖1），并以此為向導，層層展開后續知識點。物理化學很多內容都可以按照“現象→原因→影響因素→相關現象”模式引入知識點，然后通過“定量概念→理論推導→結論→應用計算”模式，結合數學方法和公式定量表達知識點。在界面化學、極化現象、溶液吸附等都可采用“邏輯地圖”的方式，順著邏輯關系進行講解，這樣學生不僅能思路清晰地接受和理解新知識，還自發地構建知識點的內在邏輯聯系。

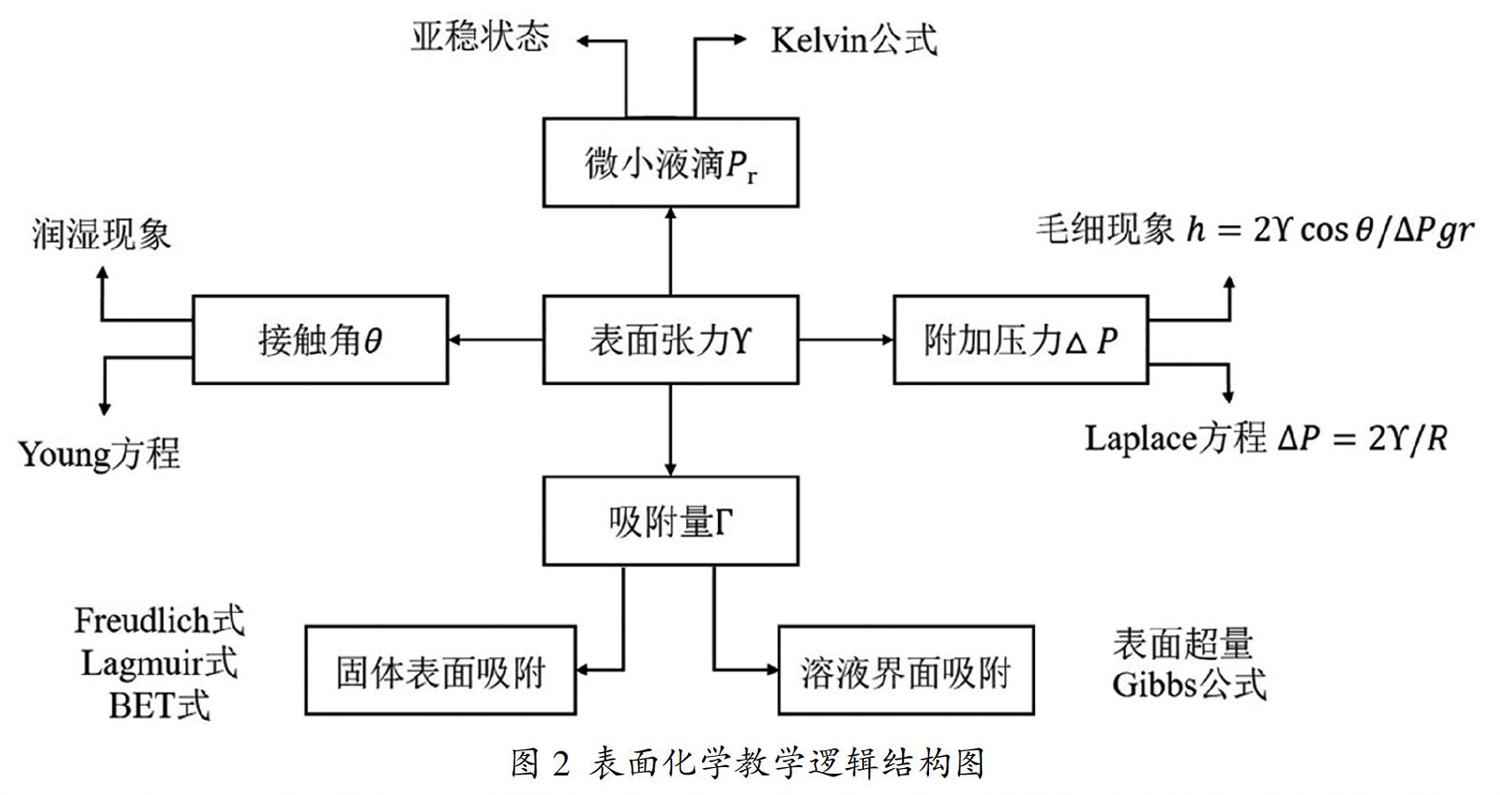
在物理化學一章或一個理論結束時，同樣可以利用邏輯結構圖進行總結。通過邏輯結構圖進行回顧，對該部分的內容進行整體性的邏輯結構分析，幫助學生梳理知識點之間的相互聯系和邏輯關系。在教學中，應注重挖掘各部分的內容間的橫向邏輯關系，力求串聯先前學過的知識點，構建基于內在邏輯關系的立體網絡知識體系，并外化于簡明的邏輯圖。這種方法可以有效促進學生“零存整取”，加深對物化知識的整合加工。例如，表面物理化學部分，可以統一在“表面張力”為中心的邏輯圖中（如圖2）。

此外各章知識點的關聯（如熱力學第二定律與化學平衡、熱力學與電化學的關聯等）也可采用邏輯結構圖輔助教學。教學實踐表明，靈活運用邏輯結構圖，教學思路清晰明了。不僅幫助學生從內在邏輯結構層面整體把握物化知識，而且還充分調動學生的邏輯思維活動，于無形中培養了學生的邏輯思維能力。

四、適時穿插邏輯思維方式，培養學生科學思維能力

物理化學蘊含著豐富的邏輯思維方式，歸納與演繹、類比、假說與模型化、逆向思維等基本邏輯思維方式展現得淋漓盡致。教學時除了傳授物化知識，應注重適時穿插邏輯思維方式，揭示物化知識背后的邏輯思維軌跡，讓學生感受邏輯思維的魅力，逐步形成邏輯思維習慣。以下為作者在物化教學中穿插基本邏輯思維方式的經驗：

（一）歸納與演繹

歸納與演繹是邏輯思維的基本方式。歸納是在大量已知的事實的基礎上，概括出一般性結論的思維方式，其特點是從特殊到一般。熱力學第一、第二定律就是在總結人類大量的實踐經驗和科學實驗基礎上得出的。熱力學第一定律是從大量的能量轉換的事實歸納而來。熱力學第二定律同樣如此：開爾文從熱功轉換角度總結出“不可能從單一熱源吸取熱量使之完全轉化為功而不產生其他影響”;克勞修斯則從傳熱角度將其歸納為“熱不可能從低溫物體傳到高溫物體而不產生其他影響”。熱力學兩大基本定律奠定了熱力學發展的基礎，可見科學歸納一些實驗事實和現象，有望為科學的進步和發展做出重大貢獻。

演繹則是從普遍性的理論和知識出發去認識特殊和個別現象的思維方式，其特點是從一般到特殊。物理化學很多定義和公式的推導都運用到演繹的思維方式。在教學過程中，除了公式推導外，還應深入剖析公式推導過程所運用的思維方式，訓練學生的邏輯思維。焓是在熱力學第一定律的基礎上演繹而來，其演繹過程如下：假設系統變化為等壓過程且不做非體積功，則有U2-U1=Qp-p（V2-V1），移項整理可得Qp=（U2+V2）-p（U1+pV1），從而定義了狀態焓（H=U+pV）。演繹的思維方式同樣適用于吉布斯自由能和亥姆霍茲自由能的推導。熵判據只適合隔離系統，因此實際應用比較困難。針對該問題，亥姆霍茲創新地應用“組合思維”，聯合熱力學第二定律（dS-δQ/Tsur≥0）與第一定律（δQ=dU-δW）推導并定義了亥姆霍茲自由能（A=U-TS）和亥姆霍茲判據（-δW≤-dA）。吉布斯采用類似的方法進行演繹，并應用“拆分思維”將功拆分為膨脹功和非膨脹功，從而推導出等溫等壓條件下的吉布斯自由能和吉布斯判據。

（二）類比法

類比通常建立于客觀事物之間的普遍關聯性基礎之上，對具有同一性或類似的兩類對象的聯想和比較。物理化學很多公式的推導就運用了類比思維，實際氣體的范德華方程就是典型的例子。實際氣體范德華方程（公式2）就是在比較與理想氣體的偏差，在理想氣體狀態方程（公式1）的基礎上進行體積修正項b和壓力修正項a/V。維利方程（公式3）同樣源自類比理想氣體狀態方程而來。

物理化學很多公式形式上高度相似，邏輯上可類比。教學中可適時將這些公式類比關聯起來。這樣不僅可以加強學生的理解和記憶，還能幫助學生將分散的知識點整合形成知識體系。例如，范特霍夫滲透壓公式（ΠV=nBRT）時，可以類比學生比較熟悉的理想氣體狀態方程（pV=nRT）。又如在相平衡、化學平衡、化學動力學出現了3組類似的方程式，即克-克方程（公式4）、范氏方程（公式5）、阿氏方程（公式6）。這三個方程式都反映溫度對體系的影響。具體而言，克-克方程則反映溫度對相平衡的影響，范氏方程反映溫度對化學平衡的影響，阿氏方程表示速率常數與溫度之間的關系。稀溶液兩大經驗定律的拉烏爾定律（pA=p*xA）和亨利定律（pB=kx，BxB）同樣可以類比。兩個定律說明溶劑（或揮發性溶質）的分壓與其組成呈線性關系，從而可將線性方程組合形成蒸氣組成圖與壓力組成圖。課堂上鼓勵學生運用類比思維，發現知識點的相似點和共性，有利于記憶理解并提升邏輯思維品質。

此外，還可運用類比方法，將物理化學與其他學科進行聯系起來。相平衡的杠桿規則可與中學物理的力矩平衡類比起來，這樣學生就容易掌握。活化能是化學動力學一個難點內容，教學中可類比俗語“鯉魚躍龍門”（出自《埤雅·釋魚》，原文為“魚躍龍門，過而為龍，唯鯉或然”）。活化能是指化學反應中反應物到達活化分子狀態所需的最低能量。可以將反應物、活化能、產物分別類別于鯉魚、龍門山、龍。反應提供的能量必須高于活化能才能生成產物，就好比鯉魚只有越過龍門山才能化身為龍。催化劑可以通過降低活化能加快反應速度，但不能改變平衡。同樣以此類比，催化劑好比穿山隧道，鯉魚不用躍龍門，直接游過隧道便可修成正果。

（三）假說與模型化思維

科學假說指依據科學原理和事實對所研究的自然現象及其規律性提出的一種假定性的推測，而模型化思維是根據科學實驗和理論所建立的真實模型或理想模型。模型化思維是通過建立理想模型，略去非本質的次要因素，使問題簡單化，從而也易于找出各基本因素之間的相互關系;然后，再逐步予以修正，使之可用于實際體系。這類理想模型主要有理想氣體模型、理想液態混合物模型、理想吸附模型等。

適當介紹理想模型的思維方式，可以讓學生深刻認識實際體系與理想模型的差別，更重要的是讓學生領會理想模型科學思維方式。譬如，理想氣體模型：將氣體分子視為無體積的質點、分子間無相互作用力，得到理想氣體狀態方程（公式1）。而實際氣體則需要考慮氣體分子自身的體積和分子間相互作用力。因此需要在理想氣體的基礎上對壓力和體積進行修正，得到實際氣體的狀態方程（公式2）。又如，理想液態混合物模型假設任一組分在全部濃度范圍內都遵從拉烏爾定律。光學異構體的混合物、同位素化合物的混合物、立體異構體的混合物以及緊鄰同系物的混合物可近似看作理想液態混合物。相較于理想液態混合物的化學勢（μB（l）=μ（l）+RTInxB），實際溶液的化學勢（μB（l）=μ（l）+RTInxB）只是在濃度項進行了校正。化學動力學也不乏模型化思維，復雜化學反應化學的平衡態與穩態相當于一個模型邊界條件。

教學中適時剖析理想模型建立過程中內在邏輯與思路，能讓學生茅塞頓開、豁然開朗。例如，卡諾循環的建立是為了解決熱機效率的極限問題，即哪種熱機效率最高。顯然，疑問，用熱量最少且做功最大的熱機效率最高。此時，可借機向學生拋出問題“如何設計這樣一個熱機呢？”，引導學生利用“可逆過程環境對系統做最小功，系統對外做最大功”的知識點，設計出效率最高的熱機即卡諾可逆熱機。與實際熱機相比，卡諾可逆熱機不考慮活塞與缸體間的摩擦力等次要因素，充分彰顯了抓主要矛盾的科學思維方法。該理想模型不僅解決了熱機效率極限問題，還演繹出了卡諾定理，并在此基礎上發展了熱力學第二定律。

五、結束語

物理化學是一門重要化學化工專業基礎課程，具有概念繁多、理論抽象、公式繁雜且應用條件嚴苛等特點。同時它又蘊含了許多精妙獨特的邏輯思維方法。基于物化課程的特點，我們嘗試剖析物化原理、概念與公式背后的邏輯思維方法，并將其貫穿于整個課程教學過程。已初步形成培養學生邏輯思維能力的方法：靈活運用邏輯結構圖，巧妙借用高等數學思維，適時穿插邏輯思維方式。教學實踐表明，這不僅有利于學生掌握和理解物化知識，同時強化了邏輯思維訓練，提高了學生的邏輯思維能力，為將來從事創新創業等工程實踐活動打下了堅實的基礎。總之，邏輯思維能力是新工科背景物理化學教學改革的重要方向，值得努力探索和實踐。

參考文獻：

[1]胡波，馮輝，韓偉力，等.加快新工科建設，推進工程教育改革創新——“綜合性高校工程教育發展戰略研討會”綜述[J].

復旦教育論壇，2017，15（2）：20-28.

[2]“新工科”建設行動路線（“天大行動”）[J].高等工程教育研究，2017（2）：24-25.

[3]吳愛華，侯永峰，楊秋波，等.加快發展和建設新工科主動適應和引領新經濟[J].高等工程教育研究，2017（1）：1-9.

[4]華東師范大學哲學系邏輯學教研室.形式邏輯[M].上海：華東師范大學出版社，2009.

[5]國家教委社科司組編.自然辯證法概論（修訂版）[M].北京：高等教育出版社，2001.

[6]梁延高.形式邏輯和熱力學第二定律中幾個重要命題的證明[J].四川師范大學學報，1986（3）：82-84.

[7]趙月春，李明華.物理化學課的邏輯結構教學法[J].高等農業教育，2001（8）：55-57.

[8]齊珊，邢軍，馬克東，等.大學化學教學中培養學生邏輯思維能力的基本路徑[J].化學教育，2014，35（8）：20-22.

[9]吳晗清，鄭冬梅，李遠蓉.化學問題解決中的科學方法教育[J].化學教育，2011，32（3）：3-5.

[10]陳麗琴，胡志剛.歸納法與演繹法在化學教學中的應用[J].化學教育，2013，34（6）：47-49.

[11]傅獻彩，沈文霞，姚天揚，等.物理化學[M].北京：高等教育出版社，2005.

[12]楊宇.物理化學中的科學思維方法[J].廣州化工，2011，39（18），168-169.

[13]馮良東.在物理化學教學中加強學生的邏輯思維能力[J].輕工科技，2009，25（3）：149-150.

[14]韓璐，羅世永，李路海.類比思維能力的培養及在提升物理化學教學效果中的應用[J].教育教學論壇，2016（22）：238-239.

[15]萬會達，吳海燕，高海燕.類比聯想思維在物理化學教學中的應用[J].廣州化工，2015（16）：215-216.

[16]徐政久，李作駿.論化學動力學中穩態處理[J].化學通報，1987（6）：47-48.

*基金項目：2019年湖南省普通高校教學改革研究項目“化學化工類新工科卓越拔尖人才四維一體培養模式探索”（編號：2019533）;2018年湖南工業大學教育教學改革項目“面向‘新國標理工融合的化學生物類專業人才培養創新研究”（編號：2018D01）

*通訊作者：賀全國（1973-），男，漢族，湖南常德人，博士，教授，博士研究生導師，研究方向：物理化學教研、納米材料化學與物理等。