覆蓋雙向S-粗集模型的構(gòu)造及其拓?fù)湫再|(zhì)研究

田衛(wèi)章

(商丘職業(yè)技術(shù)學(xué)院，河南 商丘 476100)

引言

現(xiàn)今，研究人員都已經(jīng)充分認(rèn)知到，在Z.Pawlak所提出的粗糙集模型內(nèi)，論域上的等價關(guān)系發(fā)揮著非常關(guān)鍵性的作用.首先，在等價關(guān)系基礎(chǔ)上形成劃分；其次，再進行論域上的上近似算子以及下近似算子的構(gòu)建，即進一步精確概念，用于對不精確對象進行刻劃；最后，更加深入地探究相關(guān)的知識獲取以及知識約簡方面的問題[1-4].

然而，對于諸多實際應(yīng)用而言，構(gòu)建對象之間的等價關(guān)系存在極大的難度，甚至在對象之間就本質(zhì)層面而言并非存在等價關(guān)系，某些情況下論域也不具備靜態(tài)性特征.出于使粗糙集理論與應(yīng)用對象得到有效擴大的目的，基于相應(yīng)的研究問題，研究者對Z.Pawlak所提出的粗糙集模型開展了多元化、多樣化的推廣.在此過程中有諸多理論模型先后被提出，包括模糊粗糙集模型、程度粗糙集模型、粗糙集模糊模型、變精度粗糙集模型、以動態(tài)集合為基礎(chǔ)的S-粗糙集模型[5-6]與以覆蓋理論為基礎(chǔ)的S-粗糙集模型[7]等.本文在文獻[7]的基礎(chǔ)上，對覆蓋雙向S-粗糙集模型以及此類模型的部分性質(zhì)展開了更為深入的探究.

1 預(yù)備知識

1982年，波蘭數(shù)學(xué)家Z.Pawlak提出了粗糙集理論.其作為一類數(shù)學(xué)工具主要用于處理不確定知識.當(dāng)前，粗糙集理論被廣泛用在機器學(xué)習(xí)、數(shù)據(jù)挖掘以及模式識別等領(lǐng)域.然而，在經(jīng)典粗糙集模型中，雖然等價關(guān)系發(fā)揮著非常關(guān)鍵的作用，但等價關(guān)系的規(guī)定太過嚴(yán)格，由于等價關(guān)系只能夠解決部分完備信息系統(tǒng)，如此在一定程度上對粗糙集理論的應(yīng)用產(chǎn)生了限制.在現(xiàn)實應(yīng)用中，諸多研究人員對經(jīng)典粗糙集模型實施了推廣處理，即推廣為包括相似關(guān)系等在內(nèi)的其它關(guān)系，由此來促進此模型的發(fā)展.

其中[x]R={y∈U;(x,y)∈R}為x關(guān)于R的等價類.下近似與上近似也可用下面的等式表達：

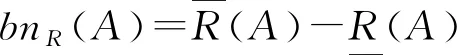
定義2(以覆蓋理論為基礎(chǔ)的S-粗糙集模型)假定X*為論域U上的雙向S-集合，X*?U；f∈F為論域U上定義的元素遷移，而且

X*=X′∪{u|u∈U,u?X,f(u)∈X} 其中X′是X的虧集[5].

如果記(R,F)°(X*),(R,F)°(X*)分別是X*?U的下近似，上近似，則有

(R,F)°(X*)=∪[x]R={x|x∈[f(x)]R∪[x]R?X*}

(R,F)°(X*)=∪[x]R={x|x∈[f(x)]R∩X*≠φΛ[x]R∩X*≠φ}

定義3[5]集合對((R,F)°(X*),(R,F)°(X*))叫做X*的雙向S-粗集. 為了書寫方便，本文用U±表示雙向S-粗集.

定義4設(shè)U±是雙向S-粗集，P(U±)是U±的雙向S-粗子集族，C?P(U±)，如果φ?C且∪C?U±，則稱C是U±的一個覆蓋，(U±,C)是一個覆蓋雙向S-粗集.

定義5設(shè)(U±,C)是一個覆蓋雙向S-粗集：

1)x∈U±，x關(guān)于(U±,C)的最小描述md(x)進行如下定義：

md(x)={K∈C;x∈K∧?S∈C(x∈S∧S?K→S=K)}.

進而可做出如下定義，md(x)為cv(x)內(nèi)涉及包含關(guān)系的極小元組成的集合，同時

cv(x)={K∈C;x∈K}.

易知，若(U±,R)是一個雙向S-粗集，R是U±上的一個等價關(guān)系，對于任意x∈U±，記[x]R={y∈U±;(x,y)∈R}為x關(guān)于R的等價類，則：

也就是說覆蓋雙向S-粗集模型是雙向S-粗集的推廣模型.

2 主要結(jié)果

2.1 覆蓋雙向S-粗集的拓?fù)?/h3>

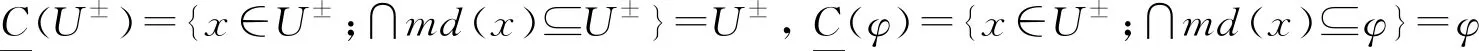
可得U±,φ∈T.

={x∈U±;∩md(x)?A}∩{x∈U±;∩md(x)?B}

故X,Y∈T時，有X∩Y∈T.

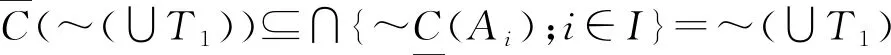
2.2 雙向S-粗集的覆蓋

引理2設(shè)(U±,R)是一個雙向S-粗集，此雙向S-粗糙集內(nèi)R屬于傳遞、自反關(guān)系，可對CR?P(U±)進行下述定義：

CR={RS(x);x∈U±}，那么可將CR視為雙向S-粗糙集的1個覆蓋，同時針對任意x∈U±，可得∩md(x)=RS(x).

由于R為自反關(guān)系，故對于任意x∈U±，x∈RS(x)，則CR組成U±的1個覆蓋.針對任意x∈U±，如果K∈md(x)，令K=RS(y)，則x∈RS(y).由此針對任意z∈RS(x)，通過(x,z)∈R且(y,x)∈R，再加上R的傳遞性，能夠明確(y,z)∈R，進而可推導(dǎo)出z∈RS(y)，因此RS(x)?RS(y)，如此可確定RS(x)為md(x)內(nèi)涉及集合包含關(guān)系的最小元，故∩md(x)=RS(x).

推論1若(U±,R)是一個雙向S-粗糙集，此雙向S-粗糙集內(nèi)，R屬于1個自反、傳遞關(guān)系，那么，RCR=R.

推論2假定(U±,C)為一個基于覆蓋理論的雙向S-粗糙集，針對任意x∈U±，將md(x)以及md′(x)依次記為x關(guān)于(U±,C)以及(U±,CRC)的最小描述，那么，md(x)=md′(x).

2.3 覆蓋雙向S-粗集的部分性質(zhì)

定理1自反、傳遞關(guān)系下的雙向S-粗集與覆蓋雙向S-粗集是等價的[6].

由引理2及其推論易證.

定理2設(shè)(U±,C)是一個覆蓋雙向S-粗集，則對于任意A?U±，有如下關(guān)系成立：

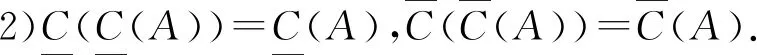
由覆蓋雙向S-粗集的概念和經(jīng)典粗糙集的有關(guān)性質(zhì)，不難證明結(jié)論成立.

定理3設(shè)(U±,C)是1個基于覆蓋理論的雙向S-粗糙集，對U±上二元關(guān)系RC進行下述定義：

針對任意(x,y)∈U±，(x,y)∈RC當(dāng)且僅當(dāng)y∈∩md(x)時，RC是U±上的1個傳遞、自反關(guān)系.

如此能夠獲得如下證明，針對任意x∈U±，關(guān)注到x∈∩md(x)，因此，可認(rèn)為RC是U±上的1個自反關(guān)系；針對任意x,y,z∈U±，若(x,y)∈RC，(y,z)∈RC，則y∈∩md(x).如此可理解為，針對任意K∈md(x)，同時再結(jié)合y∈K，可發(fā)現(xiàn)K1∈md(y)，使得K1?K，由此∩md(y)?∩md(x).因此，通過z∈∩md(y)能夠得到下式：z∈∩md(x)，進而可明確(x,z)∈RC，如此即可判定RC為U±上的1個傳遞關(guān)系.

3 結(jié)語

本文主要給出了覆蓋雙向S-粗糙集模型以及此類模型的部分基本性質(zhì).若按照文獻[8]的研究思路，進行基于覆蓋理論的雙向S-粗糙模型的確定增值算子以及不確定增值算子的構(gòu)建，則同時能夠在一定程度上實現(xiàn)對近似算子性質(zhì)的改進.關(guān)于這一問題，我們將另文研究.