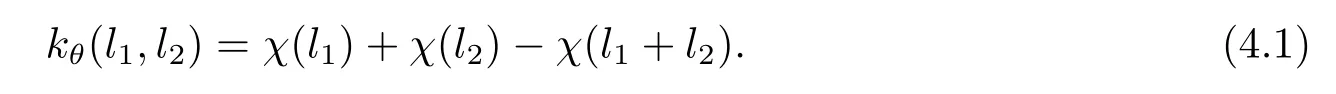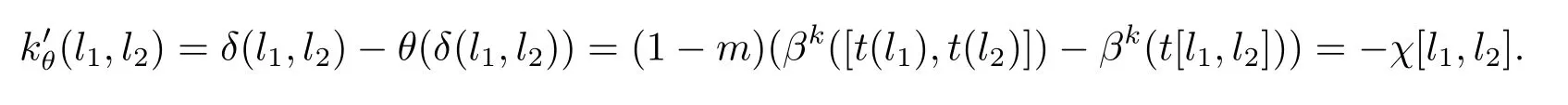阿貝爾hom-李環擴張的自同構

徐曉寧賴 燕

(1.遼寧大學數學院,遼寧沈陽 110036)

(2.信陽大別山高級中學,河南信陽 464000)

1 引言

近些年來,hom-結構,如hom-李代數,hom-代數,hom-李超代數,hom-超代數,hom-雙代數,n-元hom-Nambu-李代數以及hom-李2-代數等代數結構及性質被廣泛研究,而且取得了許多重要研究結果.hom-李代數最早是由Hartwig,Larsson以及Silvestrov在文獻[1]中研究Witt代數和Virasoro代數的形變時提出來的.文獻[2]給出了hom-李代數及其表示的定義,而且對hom-李代數的表示理論進行了嚴謹細致的研究.文獻[3]在半單李代數上研究了hom-李代數的結構.二次hom-李代數在文獻[4]中得到了研究.文獻[5]提供了保積hom-李代數可解的充要條件.

而在李理論的研究中,李環是一個重要且非常有趣的課題.在文獻[6]中,研究了冪零李環的條件及冪零李環的中心序列.對于4-Engel李環的冪零類的研究在文獻[7]中得到體現.文獻[8,9]對李環的二階上同調及Schreier’s擴張理論進行了探索.特別的,在文獻[10]中,作者在李環的一個短正合序列中的A的擴張的自同構群上構造正合序列,這里A是E的阿貝爾子環.他們通過一系列的研究得出如下結論.

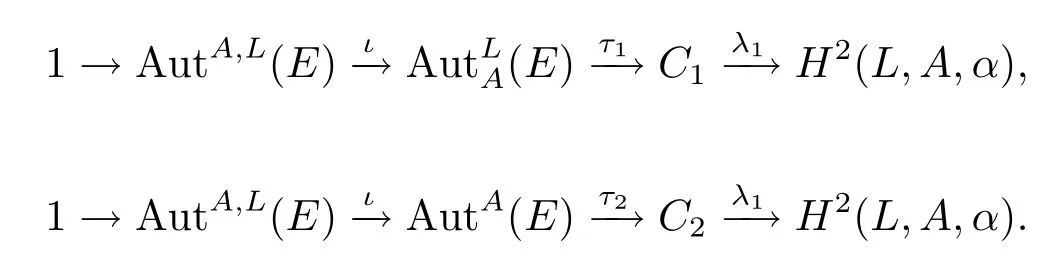
設A→E→L是中心擴張,則存在以下正合序列

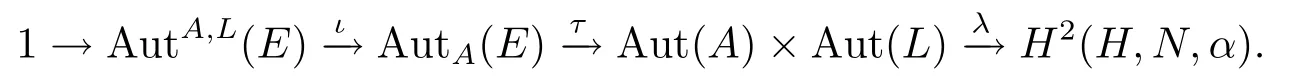
文獻[11,12]研究了有限維p-群上的p-自同構.文獻[13,14]分別在群擴張的自同構中得到了一個正合序列和在群擴張的自同構群上得到Wells正合序列.特別地,在文獻[15]中,作者在群的一個短正合序列中的N的擴張的自同構群上構造正合序列,這里N是G的阿貝爾子群.他們通過一系列的研究得出如下結論.

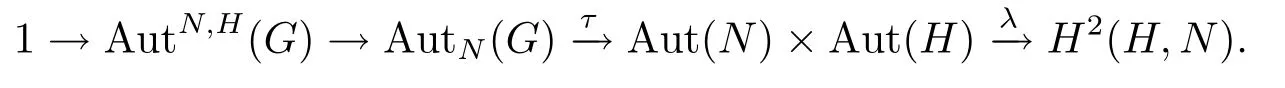
文獻[16]首次研究了hom-李環,給出了hom-李環的定義并討論了hom-李環冪零的條件.自然地,通過對阿貝爾群擴張的自同構和阿貝爾李環擴張的自同構的研究,希望在阿貝爾hom-李環中也能構造出相應的正合序列,并對其進行相關應用.本文具體結果如下:

定理1.1令是一個阿貝爾擴張,則有以下兩個正合序列:

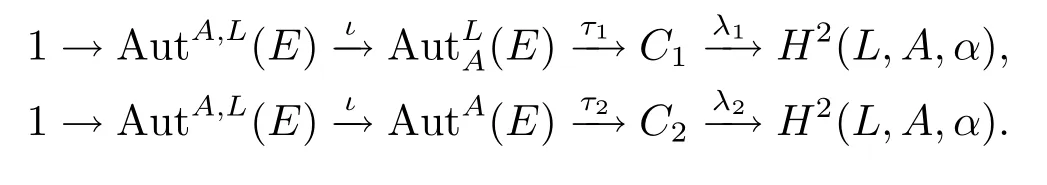
定理1.2令是一個中心擴張,則存在下列正合序列:

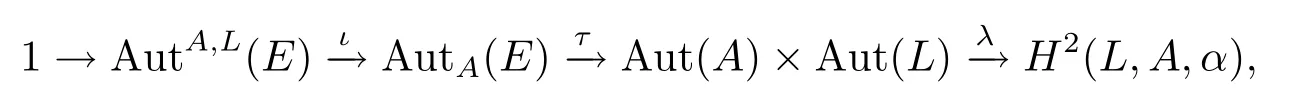
定理1.3令E是一個hom-李環,且A是E的一個阿貝爾理想,如果序列A→E→L分裂,則序列

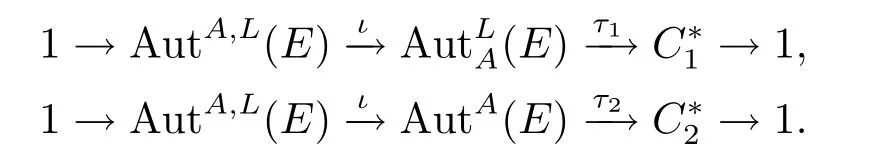
也可裂.

定理1.4令E是一個階為pn(p≥2)的hom-李p環,Z(E)是循環的且Φ(E)?Z(E).則每一個Z(E)的p自同構都可以被擴張成依賴于的E上的自同構,這里,A=Z(E),L=E/Z(E).

本文內容安排如下.第2節介紹與hom-李環及其正合序列等有關的一些基本概念.第3節,在是阿貝爾hom-李環擴張的前提下,討論了正合序列的實現過程,并給出了不同情況下的正合序列.在阿貝爾hom-李環擴張是可分裂的情況下,對不同形式擴張下的正合序列進行了改造,使得被改造后的正合序列依然可分裂.第4節,對定理3.10中所得到的正合序列(3.4)進行了應用.

2 定義

本節給出本文中將涉及的一些相關概念和基本結論.

定義2.1[16]hom-李環是指一個三元數組(L,[·,·],β),其中L是一個阿貝爾群,[·,·]:L×L→L是反對稱雙線性映射,線性映射β:L→L滿足hom-Jacobi等式

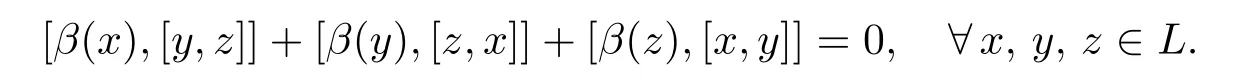
定義2.2設(L,[·,·],β)為hom-李環,若線性映射β:L→L滿足

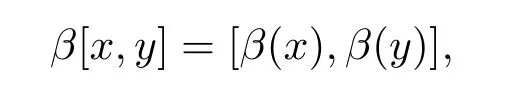
其中x,y∈L. 則稱 (L,[·,·],β)為保積 hom-李環.

定義2.3設 (L,[·,·],β)是一個 hom-李環,并且M為L的子群. 若β(M)?M,[M,M]?M,則稱 (M,[·,·],β)是 (L,[·,·],β)的 hom- 子環.若L的子群M滿足β(M)?M,[M,L]?M, 稱M為 (L,[·,·],β)的理想.

定義2.4設L為有限維hom-李環,若0令Φ(L)為L的所有極大hom-子環的交.若L=0,令Φ(L)=0,則稱Φ(L)是L的Frattini hom-子環.

定義2.5設 (L,[·,·],β)是一個保積的hom-李環,令βk=β?β?···?β,特別地β0=id,β1=β,對于任一非負整數k,一個線性映射D:L→L,如果滿足下面兩個條件

(1)[D,β]=0,

(2)D([x,y])=[D(x),βk(y)]+[βk(x),D(y)],?x,y∈L.

則稱D為hom-李環的βk導子.所有的hom-李環的βk導子的集合記為Derβk(L).

定義2.6定義hom-李環 (L,[·,·],β)的降中心列為

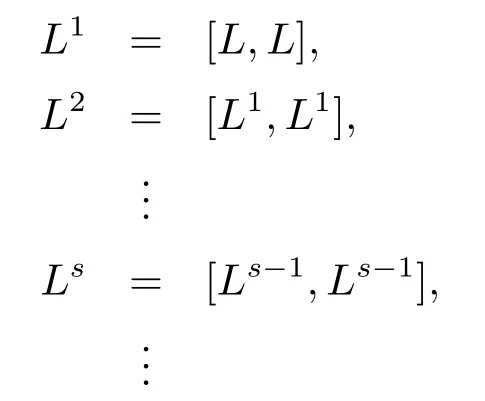
若存在n∈Z+,使得Ln=0,則 稱 (L,[·,·],β)冪零.

定義2.7令L是一個hom-李環且n∈N+,定義

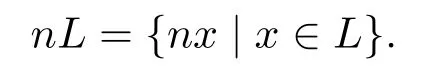
則易知nL是L的一個理想.一個冪零hom-李環L的階為p,稱L為p-hom-李環.稱L0=[L,L]為L的導出子環.

定義2.8設 (L1,[·,·],β1)與 (L2,[·,·],β2)為 hom-李環.若線性映射φ:L1→L2滿足

(1)β2φ=φβ1,

(2)φ([x,y]1)=[φ(x),φ(y)]2,?x,y∈L1,

則稱φ為hom-李環同態.當φ既是單射又是滿射時,則稱它為同構映射.

定義2.9設(L,[·,·],β)是一個hom-李環,N是L的理想.L/N={x+N|x∈L}在L/N的元素之間定義方括號積[·,·]如下

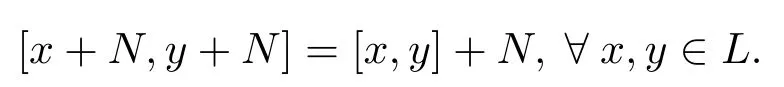
若是L/N上的一個同態且則L/N關于上述方括號積構成一個hom-李環,稱L/N為hom-李環L模掉理想N的商環,記為=L/N.

定義2.10若E→L是hom-李環的滿同態,所以對?x∈L,則存在tx∈E,使得tx→x,稱tx為x的一個提升.

定義2.11設L1,L2,···,Lk,···均為域F上的hom-李環,又fi是Li到Li+1的同態.如果 Kerfi+1=fi(Li),i=1,2,···,則稱序列

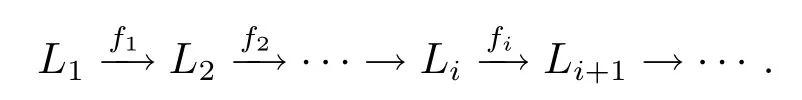
為正合序列.

定義2.12設(L,[·,·],β)是一個hom-李環,V是線性空間,并且βv是V上的線性映射.(V,βv)就被稱為hom-L-模,如果存在一個映射

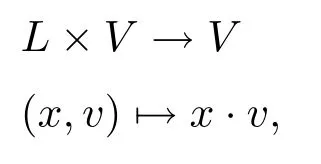
并且?v∈V,x,y∈L,滿足以下條件

(1)βv(x·v)=β(x)βv(v),

(2)[x,y]βv(v)=β(x)yv?β(y)xv.

定義2.13設a,b與L均為hom-李環,若有L的理想n與a同構,而商環L/n與b同構,則稱L是b通過a的擴張.

定義2.14設L是一個hom-李環,A是一個平凡的hom-L-模,令Z2(L,A,α)是所有函數對(f,g,α)的集合.這里f,g:L×L→A,α:L→Derβk(A),對?l,l1,l2,l3∈L滿足

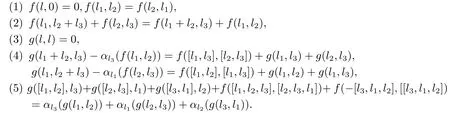
稱Z2(L,A,α)為在A上的L上的上閉鏈.

現給出兩個上閉鏈 (f,g,α),(f0,g0,α)∈Z2(L,A,α),令 (f,g,α)+(f0,g0,α):=(f+f0,g+g0,α),這里f+f0,g+g0在逐點加法(如果f,g:L×L→A,則(f,g,α)(l1,l2)=f(l1,l2)+g(l1,l2))的運算下構成阿貝爾群.

定義2.15設L是一個hom-李環,A是一個平凡的hom-L-模,令t:L→A是一個滿足t(0)=0的映射.且令B2(L,A,α)是所有函數對(f,g,α)的集合.這里f,g:L×L→A,α:L→DerβK(A),對?l1,l2∈L滿足

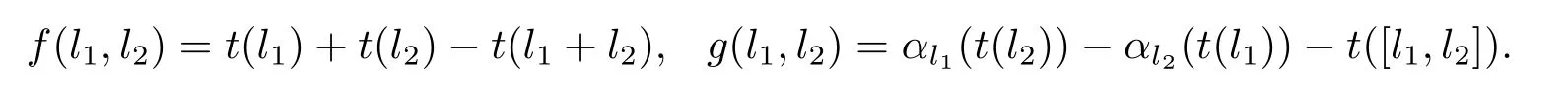
稱函數對(f,g,α)為在A上的L上的邊界余映射.

不難證明B2(L,A,α)是Z2(L,A,α)的子集.

定義2.16稱商群H2(L,A,α)=Z2(L,A,α)/B2(L,A,α).為hom-李環L的二階上同調群.

定義2.17一個被阿貝爾hom-李環A的被hom-李環L的擴張0→A→Eπ?→L→0稱為是可裂的.如果存在一個hom-李環同態λ:L→E使得πλ=1L.

3 正合序列及分裂正合序列的構造

本節的目的是構造阿貝爾hom-李環的正合序列,由于hom-李環本身內部存在一個映射和兩種運算并且還具有復雜的二階上同調群,顯然會比群和李環的構造更加復雜.在定理3.10和3.12的基礎之上通過阿貝爾李擴張推廣了三個正合序列,并證明了在序列可裂的情況下所推廣的這三個正合序列也可裂.

令E和L是保積hom-李環,A是E的理想.β:L→L限制在A上是A上的線性變換,β是同態映射且與γ,π可交換,這一規定貫穿全文.首先來介紹一些記號.

定義3.1[10]令

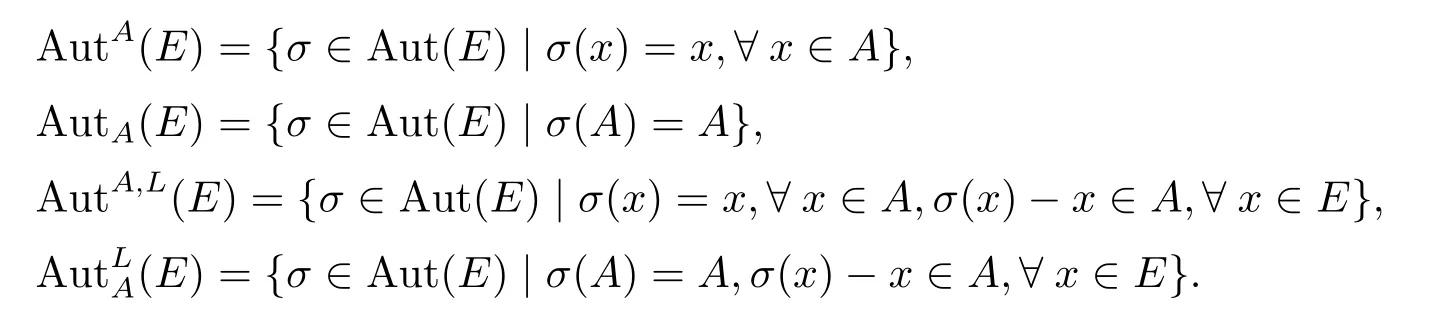
引理3.1設是一個阿貝爾hom-李環擴張,其中A是E的阿貝爾子環.則阿貝爾hom-李環A的被hom-李環E的一個擴張確定了E到A的自同構群Aut(A)的一個hom-李環同態.

證設正合列0→A→E→L→1是阿貝爾hom-李環A的被hom-李環E的一個擴張.則E→L是滿同態,進而對?x∈L,都存在一個提升tx∈E,即tx→x.于是可以規定

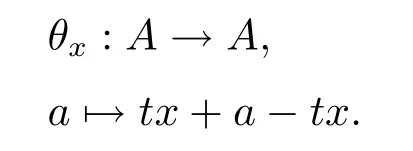
又因為A是E的hom-李環,所以Im(θx)?A,當然θx是A的一個自同構.從而存在

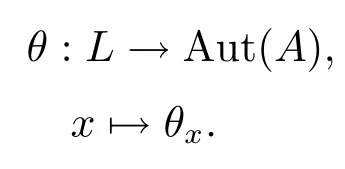
接下來利用α(l)=αl,這里αl(a)=[βk(l),a],l∈L,a∈A,來定義一個hom-李環同態α:L→Derβk(A).所以,可以考慮第二上同調群H2(L,A,α).與群和李環的情況類似,對于任意的阿貝爾擴張(θ,φ)∈Aut(A)×Aut(L)被稱為是相容的,如果?l∈L,滿足θαlθ?1=αφ(l).把所有的相容對記為C.類似于阿貝爾群擴張的Wells序列及阿貝爾李環擴張的正合序列,對每一個γ∈AutA(E)都包含了一個相容對(θ,φ),而且映射τ(γ)=(θ,φ)是一個同態.令是一個阿貝爾hom-李環擴張,其中A是E的阿貝爾子環.設t:L→E是E的一個正規截口.則對任意的l∈L,必存在一個x∈E使得π(x)=l,而且t(l)由A+t(l)=A+x所確定.這就說明了π(t(l))=l成立.

對?l1,l2∈L,定義

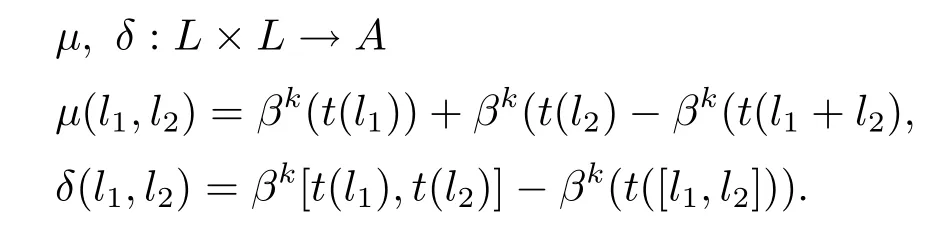
引理 3.2根據以上定義,則有 (μ,δ,α)∈Z2(L,A,α).

證要證(μ,δ,α)∈Z2(L,A,α),只需要證對?l1,l2,l3∈L有以下等式成立即可

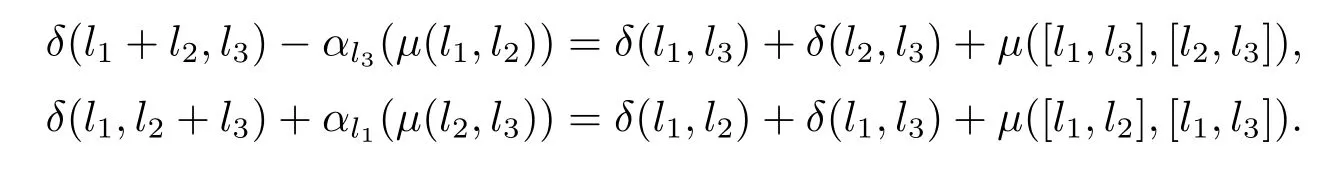
由于

且

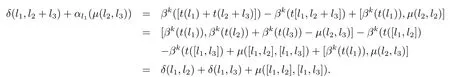
故有 (μ,δ,α)∈Z2(L,A,α).證畢.

引理3.3令A→Eπ?→L是一個阿貝爾擴張,若σ∈AutA(E),則存在一個三元組(θ,φ,χ)∈Aut(A)×Aut(L)×AL,使得對任意的l,l1,l2∈L,a∈A.有下列等式成立

(i)γ(βk(t(l)+a))=βk(t(φ(l)))+χ(l)+θ(a),

(ii)μ(φ(l1),φ(l2))?θ(μ(l1,l2))=χ(l1+l2)?χ(l1)?χ(l2),

(iii)θ[βk(t(l)),a]=[βk(t(φ(l))),θ(a)],

(iv)δ(φ(l1),φ(l2))?θ(δ(l1,l2))=χ[l1,l2]?[χ(l1),βk(t(φ(l2)))]?[βk(t(φ(l1))),χ(l2)].

證(i)令θ=γ|A,定義φ:L→L使得對任意的l∈L,滿足φ(l)=π(γ(t(l))).顯然θ∈Aut(A),φ∈Aut(L).

現在進一步定義χ∈AL,由于對任意的l∈L,都有π(t(l))=l,故有π(t(φ(l)))=φ(l),所以π(t(φ(l)))?φ(l)=0.由此,定義χ:L→A滿足χ(l)=βk(γ(t(l)))?βk(t(φ(l))).現在令l∈L,a∈A,則 得到γ(βk(t(l)+a))=γ(βk(t(l)))+θ(a)=χ(l)+βk(t(φ(l)))+θ(a).

(ii)令l1,l2∈L,根據定義有,

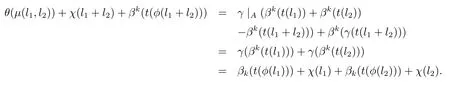
因此有,

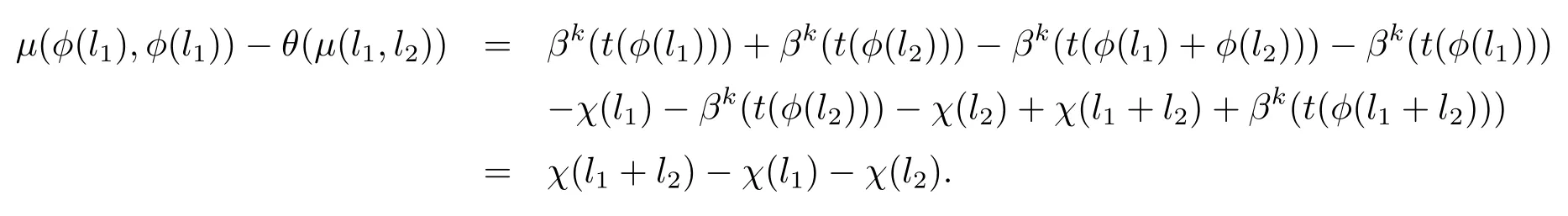
(iii)令l∈L,a∈A,故

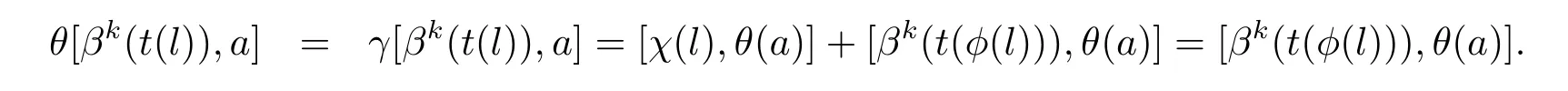
(iv)令l1,l2∈L,根據定義有,

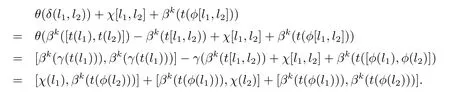
故有,

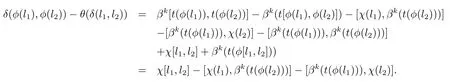
證畢.

引理3.4令是一個阿貝爾擴張,若三元組(θ,φ,χ)∈Aut(A)×Aut(L)×AL滿足引理3.3中的(ii)–(iv),則由引理3.3的(i)定義的映射γ:E→E是屬于AutA(E)中的在E上的自同構.

證首先注意到對任意的x∈E,其都可以被表示為x=βk(t(l))+a的形式.令

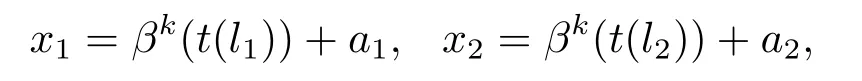
其中l1,l2∈L,a1,a2∈A.故有,

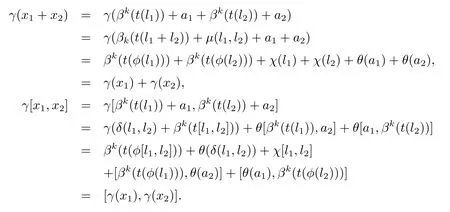
現在令x∈ker(γ),這里x=βk(t(l))+a,其中l∈L,a∈A.這意表明βk(t(φ(l)))∈A或者說φ(l)=0,因此l=0.由此可知θ(a)=0,所以x=0.故該映射是單射.下證γ是滿射.令u∈E,則可以寫成u=βk(t(l0)+a0),其中l0∈L,a0∈A.取l∈L,a∈A滿足:φ(l)=l0且θ(a)=a0?χ(l).故有,

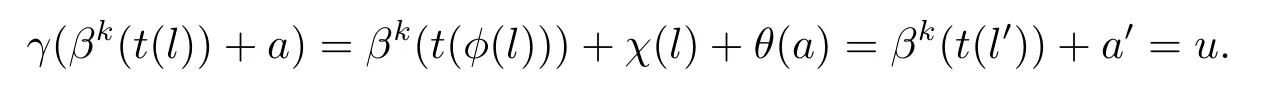
故該映射是滿射.證畢.

當A?Z(E)時,說是中心擴張.若是一個中心擴張,則L在A上的作用是平凡的,且引理3.3,3.4會有如下改變:

引理3.5令是中心擴張,若γ∈AutA(E),則存在一個三元組(θ,φ,χ)∈Aut(A)×Aut(L)×AL對?l,l1,l2∈L,a∈A滿足

(i)γ(βk(t(l))+a)=βk(t(φ(l)))+χ(l)+θ(a),

(ii)μ(φ(l1),φ(l2))?θ(μ(l1,l2))=χ(l1+l2)?χ(l1)?χ(l2),

(iii)δ(φ(l1),φ(l2))?θ(δ(l1,l2))=χ[l1,l2].

引理3.6令是中心擴張,若三元組(θ,φ,χ)∈Aut(A)×Aut(L)×AL滿足引理3.5中的(ii)和(iii),則由引理3.5的(i)定義的映射γ:E→E是屬于AutA(E)中的在E上的自同構.

引理3.7由所有的相容對組成的集合是Aut(A)×Aut(L)的子群.將所有相容對組成的子群記為C.并由此定義C1和C2如下

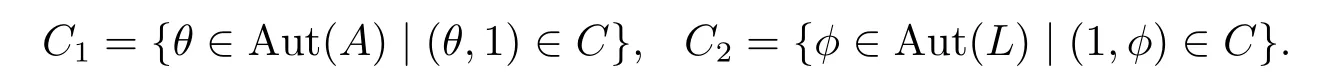
記

(i)θ∈C1?θαl=αlθ,?l∈L?θ[βk(t(l)),a]=[βk(t(l)),θ(a)],?l∈L,a∈A,

(ii)φ∈C2?αl=αφ(l),?l∈L?[βk(t(l)),a]=[βk(t(φ(l))),a],?l∈L,a∈A.

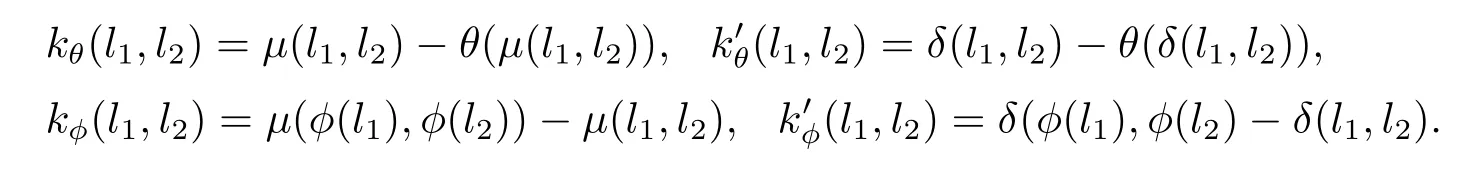
引理3.8根據以上定義是Z2(L,A,α)中的元素.

證要證只需要證對?l1,l2,l3∈L,有以下等式成立即可

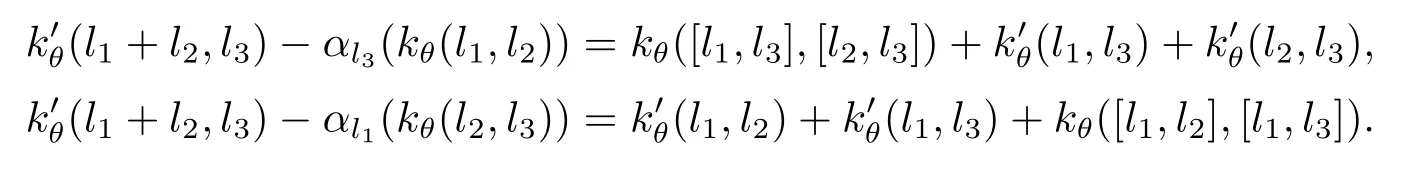
由引理3.2知以下等式成立

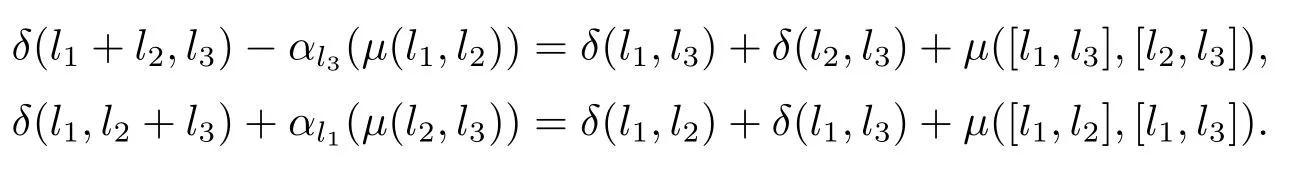
故有,

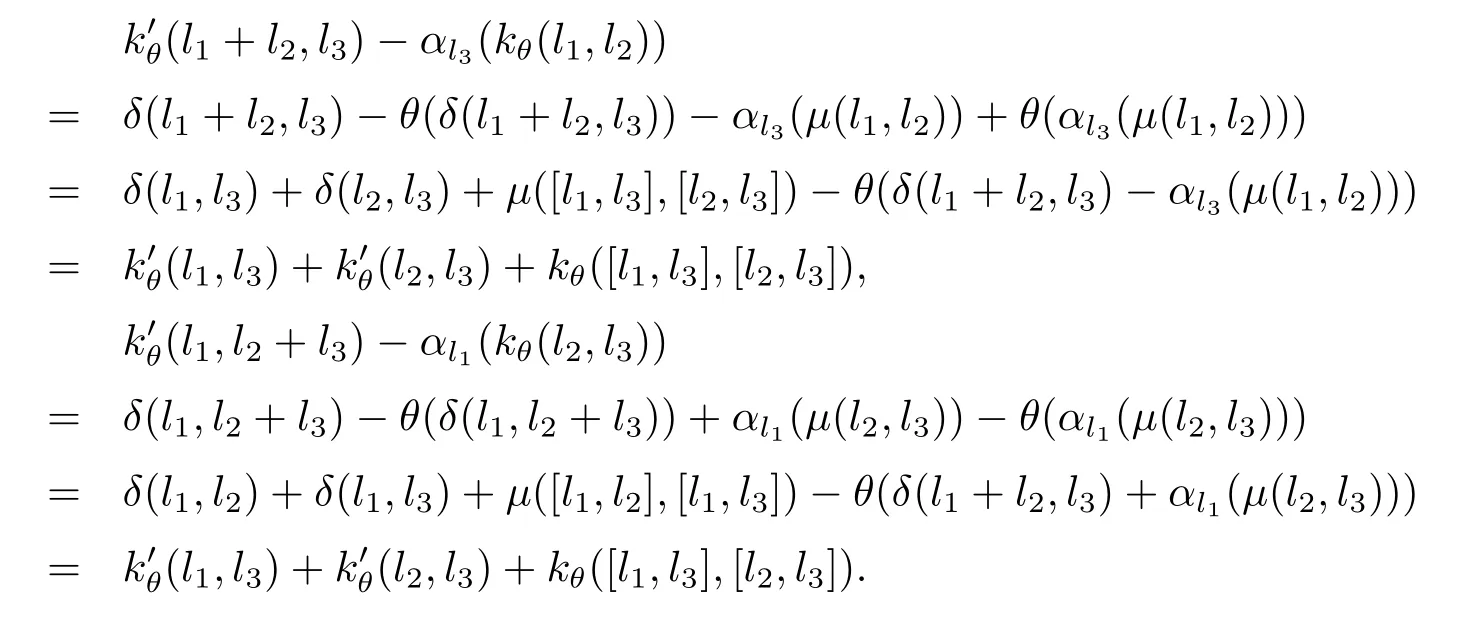
根據上面的假設和標記,定義λi:Ci→H2(L,A,α)(i=1,2)如下

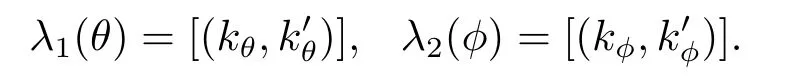
引理3.9映射λ1和λ2是定義明確的.

證首先證明λ1是定義明確的.令t,t0:L→E是兩個正常映射,則有t(l)?t0(l)∈A,?l∈L.因此對每一個l∈L都會唯一的存在λ(l)∈A使得:βk(t(l))=βk(t0(l))+λ(l).這就由等式:λ(l)=βk(t(l))+βk(t0(l)),定義了一個映射λ:L→A.又由于

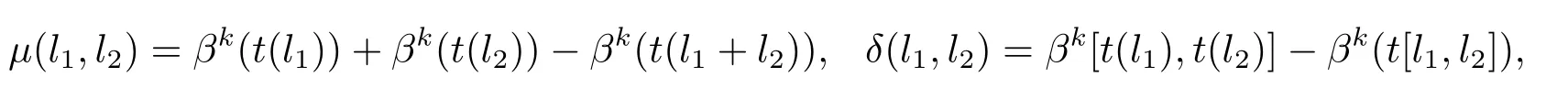
其中l1,l2∈L.同樣地,考慮t0,得到兩個映射μ0,δ0:L×L→A.使得其滿足

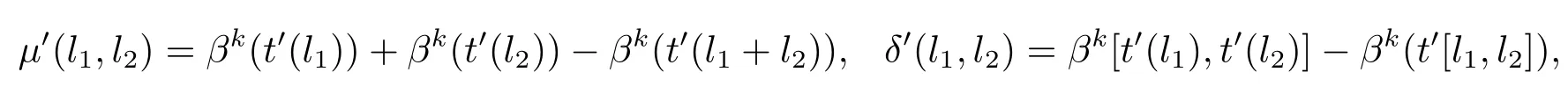
其中l1,l2∈L,可以看出

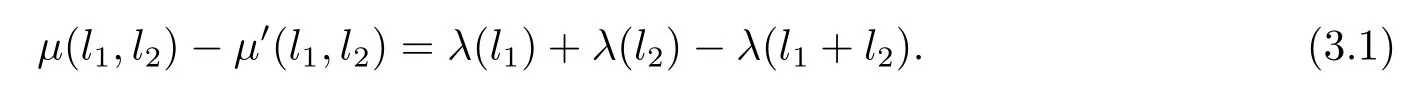
又由于

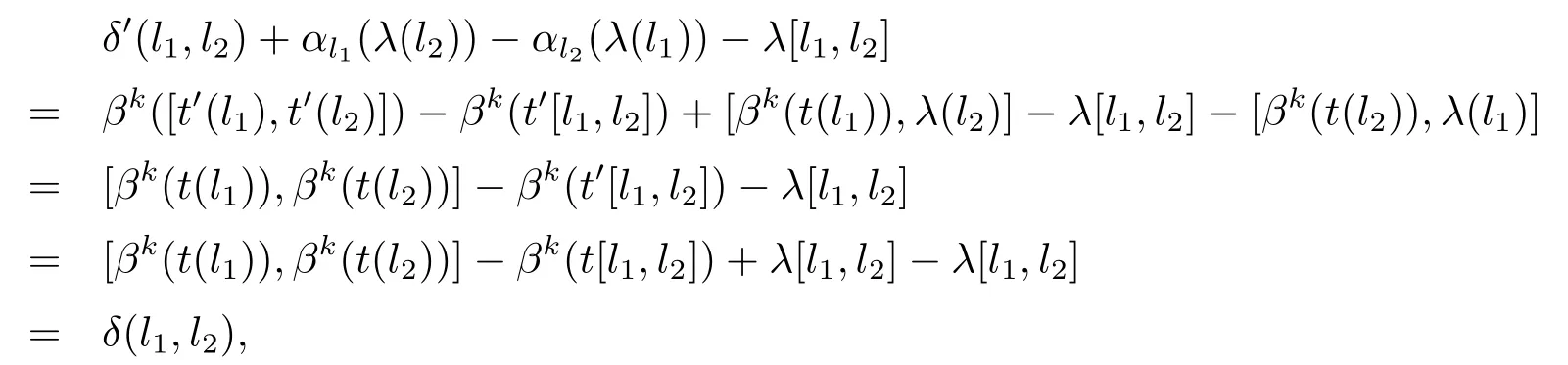
故有,

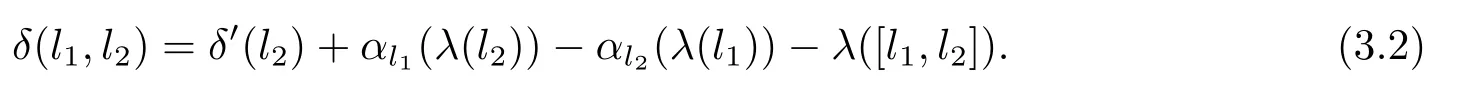
現在令θ∈C1且φ∈C2,定義映射使得其滿足

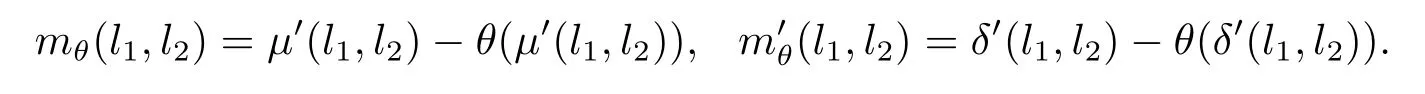
則由(3.1)式可知下面等式成立

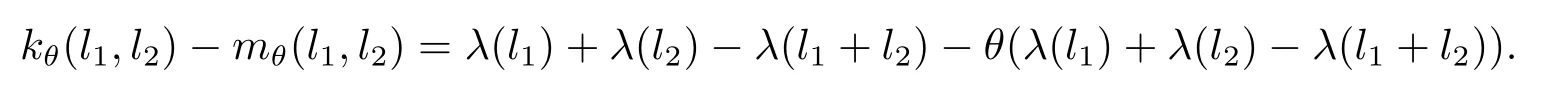
定義映射λ0:L→A使得其滿足對?l∈L都有,λ0(l)=λ(l)?(θλ)(l).自然地有,

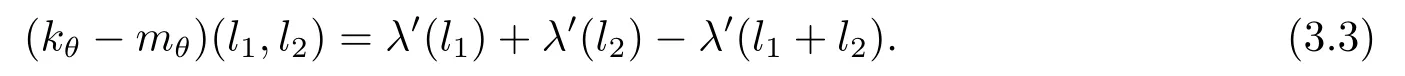
由(3.2)及θ∈C1,可以得知,

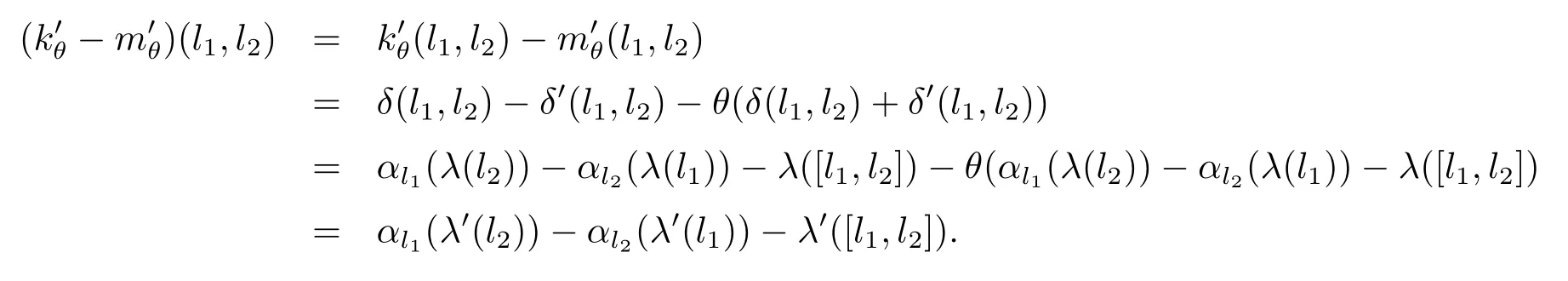
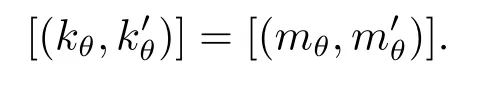
這就說明了λ1的選取不依賴于所取得空間.同理可證λ2.證畢.

注記:映射λ1,λ2不是同態映射,但這里Ker(λi)(1≤i≤2)與通常其所表示的意義一致.

定理3.10令是一個阿貝爾擴張,則有以下兩個正合序列:

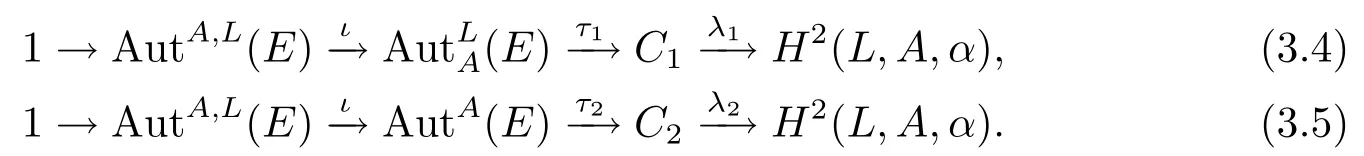
證先證(3.4),由于是顯然的.只需證即可.令有,這里θ=γ|A.因為有,φ(l)=(πγt)(l)=l.又由引理3.3可知,

下面證明Ker(λ1)?Im(τ1).設θ∈C1且滿足λ1(θ)=1.則有因此存在一個映射χ:L→A,其中χ(0)=0,滿足等式

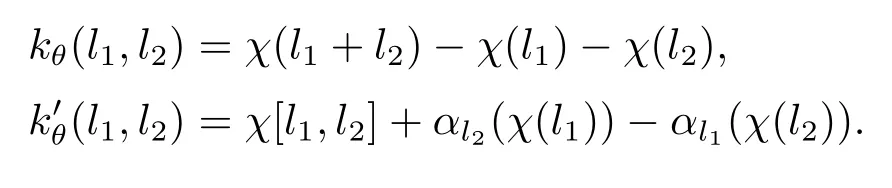
根據引理3.3,令φ=id|L,得到自同構γ∈AutA(E)滿足

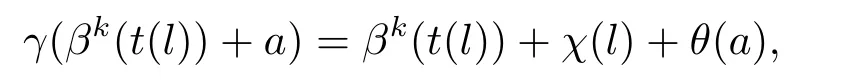
其中l∈L,a∈A.因此有,

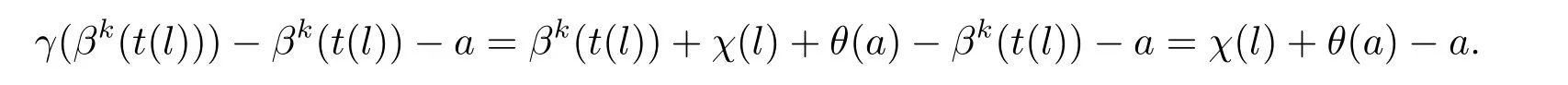
故γ(βk(t(l)))?(βk(t(l))+a)∈A.這就證明了進一步有,γ(a)=θ(a),其中a∈A.所以τ1(γ)=θ.故Ker(λ1)?Im(τ1).因此是正合列.

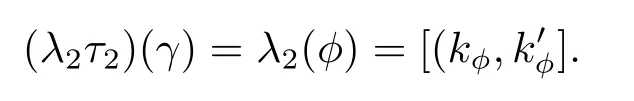
這里φ(l)=(πγt)(l),l∈L. 由于φ=τ2(γ),αl=αφ(l),由引理 3.3 的 (ii),(iv)及θ=γ|A=idA,可知,

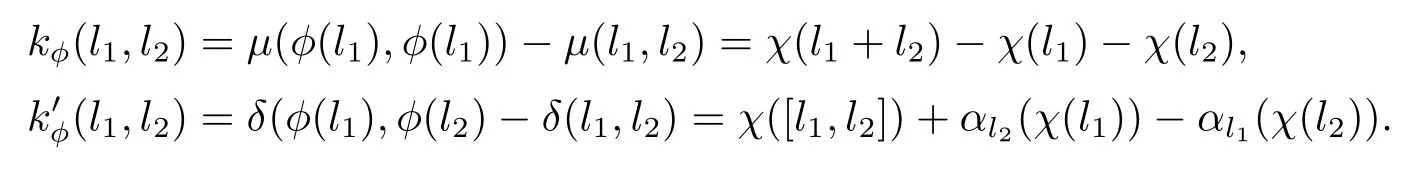
因為γ∈AutA(E),因此故Im(τ2)?Ker(λ2).

下面證明Ker(λ2)?Im(τ2).設φ∈Ker(λ2),則存在一個映射χ:L→A滿足λ(0)=0.使得,

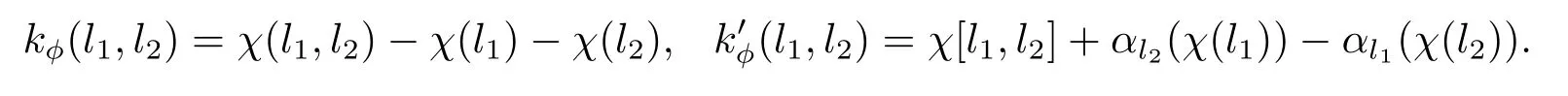
由引理3.3,令θ=id|A,則?l∈L,?a∈A,有一個自同構γ∈AutA(E)滿足

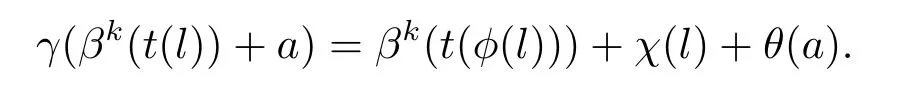
因此有γ(a)=θ(a)=a,γ∈AutA(E),且顯然有τ2(γ)=φ. 故 Ker(λ2)?Im(τ2).證畢.

引理3.11令是阿貝爾擴張且θ∈C1,φ∈C2,定義

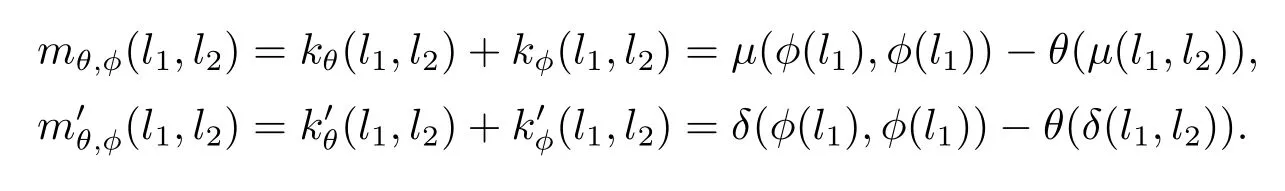
證由引理定義可知,要證只需證明以下兩式成立即可:

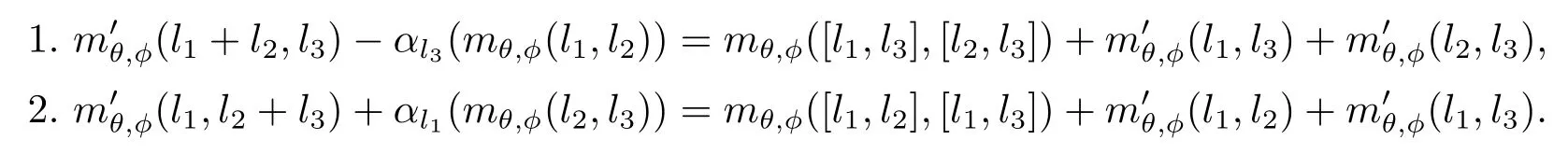
由

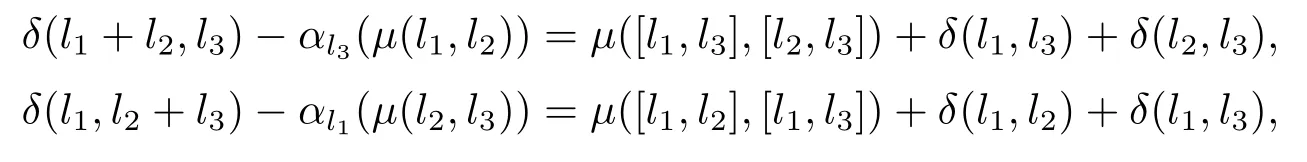
及等式

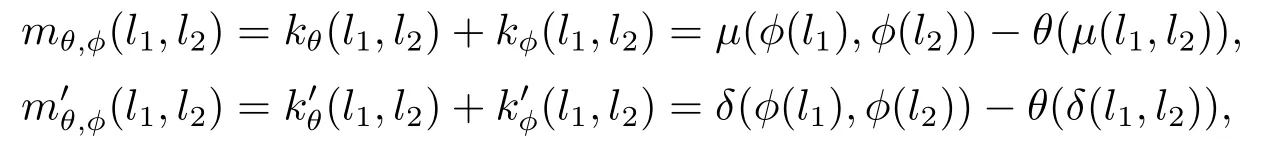
可知

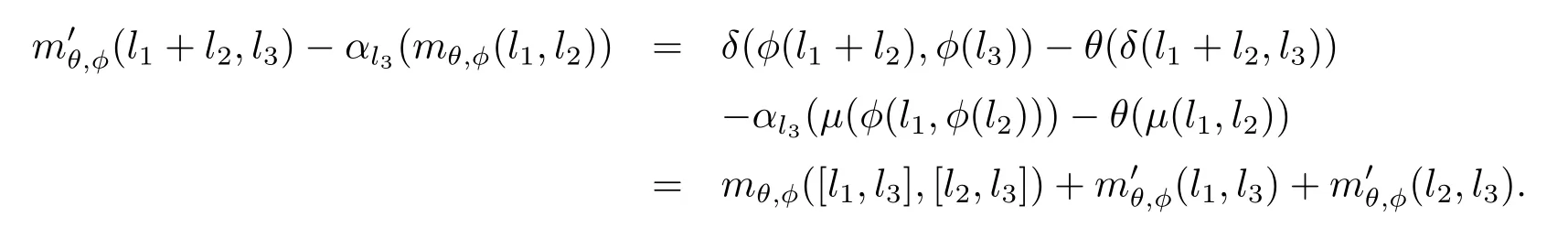
同理可證

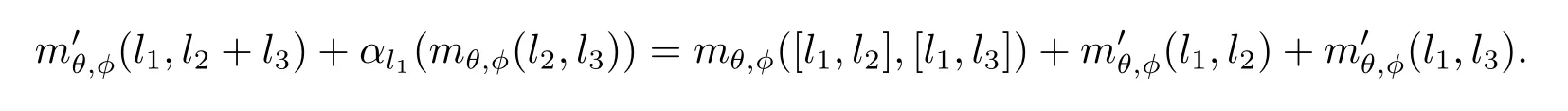
定理3.12令A→E?→πL是一個中心擴張,則存在下列正合序列:

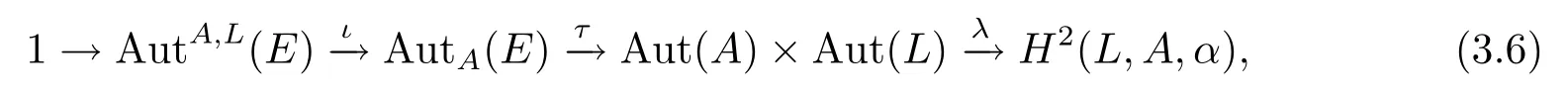
證在AutA,L(E)和AutA(E)上序列顯然是正合的.在證明此定理之前,可以證明λ是定義明確的.若(θ,φ)∈Aut(A)×Aut(L)是由γ∈AutA(E)所誘導的,則通過引理3.5的(ii)和(iii)存在一個映射χ:L→A滿足λ(0)=0使得

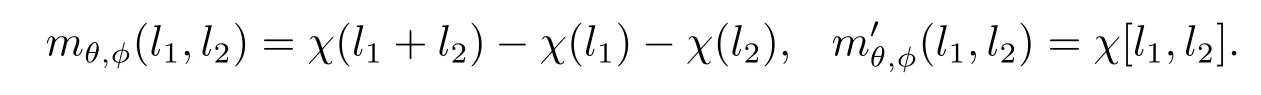
相反的, 如果 (θ,φ)∈Aut(A)×Aut(L) 滿足則存在一個映射χ:L→A滿足λ(0)=0使得

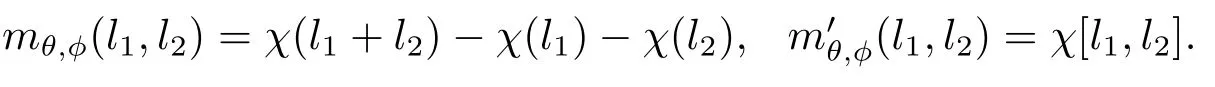
現由引理3.6知存在一個自同構γ∈AutA(E)使得τ(γ)=(θ,φ).證畢.

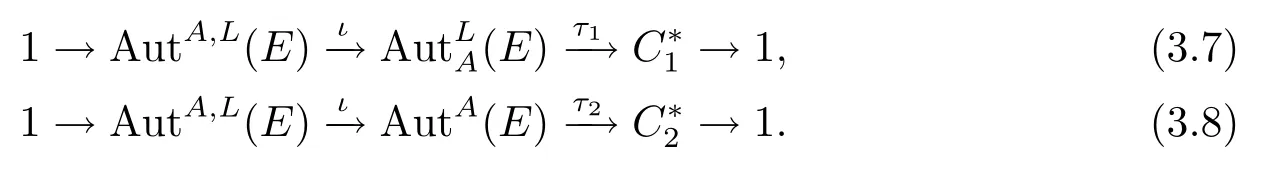
接下來,將證明如果原正合序列可裂,則這兩個正和序列也是可裂的.

定理3.13令E是一個hom-李環,且A是E的一個阿貝爾理想,如果序列A→E→L分裂,則序列(3.7),(3.8)也可裂.

證在中存在一個hom-李環同態t:L→E滿足π?t=idL,而且對E中的每個元素都可以唯一的用βk(t(l))+a表示出來,其中l∈L;a∈A.首先證明(3.7)可裂.

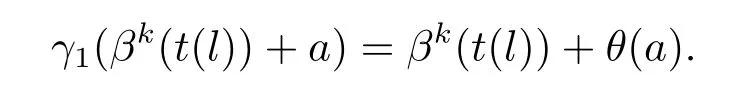
對任意的x1=βk(t(l1))+a1,x2=βk(t(l2))+a2,由于t是同構映射,則有

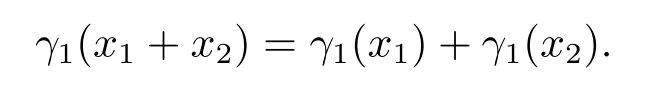
又由于θ∈C1,有,

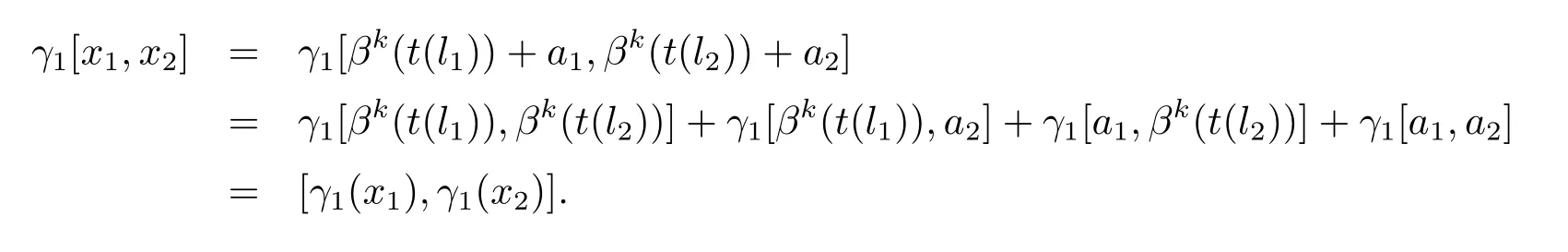
又由于γ1β=βγ1,這就證明了γ1是hom-李環同態.顯然可知:是群同態且所以序列(3.7)可裂.

現在證明(3.8)可裂.定義一個映射ψ2:C2?→AutA(E)使得其滿足ψ2(φ)=γ2,這里γ2:E→E,滿足運算

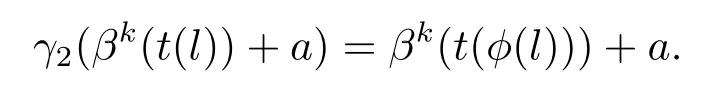
對任意的x1=βk(t(l1))+a1,x2=βk(t(l2))+a2∈E,由于t是同構映射,有,

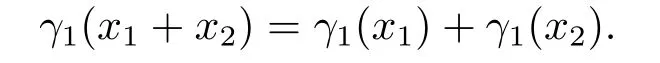
又由于φ∈C2,有αl=αφ(l),?l∈L.故

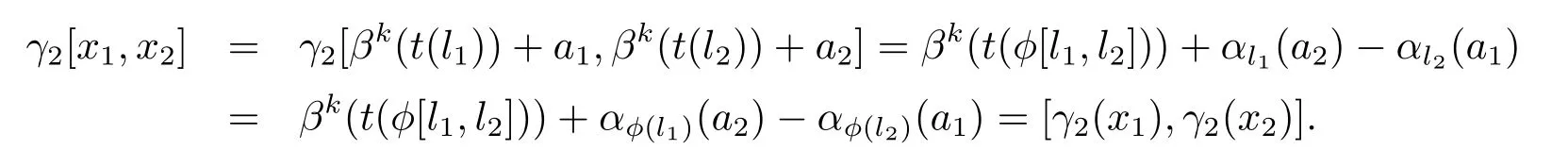
又由于γ2β=βγ2,這就證明了γ2是hom-李環的自同構,顯然可知:γ2∈AutA(E),γ2是群自同構且τ2?ψ2=idC2?.所以序列(3.8)可裂.證畢.

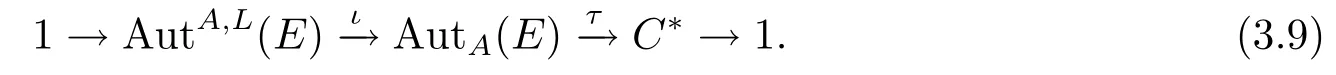
接下來,將證明如果原始的正合序列可裂,則這個正和序列也是可裂的.

定理3.14令E是一個hom-李環,且A是E的一個阿貝爾理想,進一步,若A?Z(E),如果序列A→E→L分裂,則序列(3.9)也可裂.

證在中存在一個hom-李環同態t:L→E,滿足π?t=idl,而且對E中的每個元素都可以唯一的用βk(t(l))+a表示出來,其中l∈L,a∈A.現在證明(3.9)可裂.

由ψ(θ,φ)=γ定義一個映射ψ:C?→AutA(E),這里γ:E→E,滿足運算

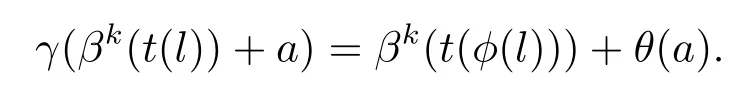
對任意的x1=βk(t(l1))+a1,x2=βk(t(l2))+a2∈E,有γ(x1+x2)=γ(x1)+γ(x2).由于t是自同態映射,且A?Z(E).可知,

又由于γβ=βγ,故γ是自同態.不難得知γ∈AutA(E),ψ是群同態,且τ?ψ=idC?.所以序列(3.9)可裂.證畢.

4 相關應用

本節,在定理3.10(3.4)的基礎上,將Z(E)的自同構推廣到E的自同構.以下引理顯然成立.

引理4.1令E是一個hom-李環.

(1)若E是阿貝爾hom-李環,則E的任何加法子群也都是E的子環.

(2)若E是不含有非平凡子環的平凡hom-李環,則E是素數階循環的.

引理4.2令M是hom-李環E的子環,取?E(M)={x∈E|[x,M]?M},則以下結論成立.

(i)?E(M)是hom-李環E的子環,且M??E(M).

(ii)M是E的一個理想當且僅當?E(M)=E.

(iii)[K,M]?M當且僅當K??E(M),這里K是E的子環.

(iv)若E是冪零的且M?E,則M??E(M).

(v)若E是冪零的,且M是E的最大子環,則M是E理想且E/M是素數階.

引理4.3令E是hom-李環,以下結論成立.

(i)若E是有限維的,則Φ(E)恰好由E的所有非生成元組成.

(ii)E/I是阿貝爾的當且僅當E0?I.

(iii)若E是冪零的,則E0?Φ(E).

(iv)若E是冪零的,則Φ(E)是E的理想.

(v)若E是冪零的且非平凡,則Z(E)0.

定理4.4令E是一個階為pn(p≥2)的hom-李P環,Z(E)是循環的且Φ(E)?Z(E).則每一個Z(E)的p自同構都可以被擴張成依賴于的E上的自同構,這里,A=Z(E),L=E/Z(E).

證令A=hxi,|A|=pω,且π:E→L是自然同態.所以得到一個中心擴張A→E→L.容易看出每一個A上的每一個循環群都保留著李乘.現在由第二章的注記得到C1=Aut(A)～=ZPω?1(P?1).注意到θ=γ|A. 因為有φ(l)=(πγt)(l)=l.所以擴張是中心擴張.定義θ:A→A滿足θ(x)=mx,這里m=1+jp且1≤m

由pt(l)∈pE?Φ(E)?A且p整除1?m,可以定義映射χ:L→A使得其滿足χ(l)=(1?m)t(l).因此,

同樣的,對?a,b∈E,有p[a,b]=0.故pE?Φ(E)?A.因此,