DIFFERENCE HARNACK ESTIMATES FOR WEIGHTED NONLINEAR REACTION-DIFFUSION EQUATIONS ON WEIGHTED RIEMANNIAN MANIFOLDS
WANG Yu-zhao,WANG Xue-ming
(School of Mathematical Sciences,Shanxi University,Taiyuan 030006 China)
Abstract:In this paper,we study the problem of difference Harnack estimate on Riemannian manifolds.By using maximum principle and weighted p-Bochner formula,we derive the Li-Yau type difference Harnack estimate and Hamilton type estimate for the positive solutions to weighted nonlinear reaction-diffusion equation on compact weighted Riemannian manifold with curvature dimension condition CD(0,N),which generalizes the non-weighted case under the condition of nonnegative Ricci curvature.
Keywords: weighted nonlinear reaction diffusion equation;Li-yau type difference Harnack estimate;hamilton type difference Harnack estimate;curvature dimension condition;weighted p-Bochner formula
1 Introduction
LetMbe ann-dimensional compact Riemannian manifold with curvature dimension conditionCD(0,N).In this paper,we consider a weighted nonlinear reaction-diffusion equation(WNRDE)

onM,whereγ>0,p>1,q>0,?p,fu=efdiv(e?f|?u|p?2?u)is the weightedp-Laplacian ofu,andfis a smooth function.
Gradient estimate or differential Harnack estimate is an important tool in geometric analysis.In 1986,Li and Yau[1] first proved the sharp gradient estimate for positive solutions to heat equation on Riemannian manifolds.Since then,gradient estimate has been studied extensively by many scholars.Particularly in the last decade,more attention has been paid to the study of nonlinear equations.Kotschwar and Ni[2]established gradient estimates forp-harmonic functions and parabolicp-Lapalacian equation on Riemannian manifolds.In[3,4],the first author and coauthor improved Li-Yau type gradient estimates for the positive solutions to the weighted nonlinearp-heat equation on Riemannian manifolds withCD(?K,m)condition.In[5],the authors proved the Li-Yau type estimate for the porous medium equation and fast diffusion equation.In[6],the first author and coauthor got sharp global Li-Yau type gradient estimates for positive solutions to doubly nonlinear diffusion equation on compact Riemannian manifolds with nonnegative Ricci curvature.
In[7],we derived the global Li-Yau type and Hamilton type gradient estimate for positive solutions to the nonlinear reaction-diffusion equation.The purpose of this paper is to extend the work in[7],that is to prove the gradient estimates for weighted nonlinear reaction-diffusion equation(1.1)on Riemannian manifolds.
To show our results,we recall some necessary notations.Let(M,g,dμ)(dμ=e?fdV)be ann-dimensional compact weighted Riemannian manifold,dVbe the Riemannian volume measure,f∈C∞(M).Define a diffusion operatorL?f= ???f·?,andN-Bakry-mery Ricci curvature tensor
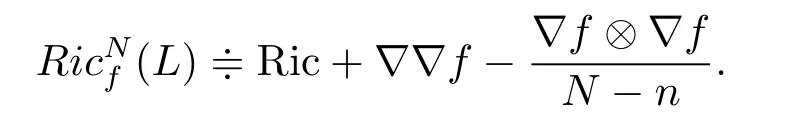
IfN=∞,then Bakry-mery Ricci curvaturewhich firstly studied by Bakry andmery[8].IfLsatisfies the curvature dimension conditionCD(K,N)if
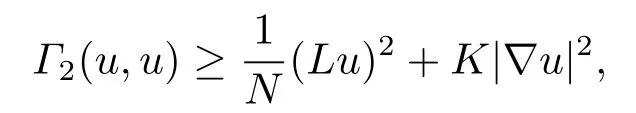
Now we give the global Li-Yau type difference Harnack estimate for WNRDE(1.1)and its applications in Harnack inequalities.
Theorem 1.1LetMbe ann-dimensional compact weighted Riemannian manifold with theCD(0,N)condition.Assume thatuis a smooth nonnegetive solution to(1.1),andsatisfy equation(2.1)onM.Then for anyb>0,aˉ>0 andc(q?1)(q?1+b)≥0,we have
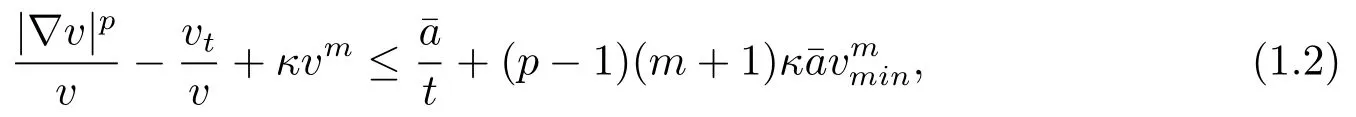
Remark 1.2Whenc=0 andf=const.,the estimate(1.2)reduces the Li-Yau type estimate of weighted doubly nonlinear diffusion equation in[6].
On the other hand,Hamilton[10]improved the elliptic type gradient estimate on a compact manifold.Yan and Wang[11]established elliptic type gradient estimates for positive solutions to the doubly nonlinear diffusion equation on Riemannian manifolds.Recently,the authors[7]derived Hamilton type gradient estimates for nonlinear reaction-diffusion equation on compact Riemanian manifold with nonnegative Ricci curvature.In this paper,we can prove Hamilton type estimate for WNRDE(1.1)onn-dimensional compact weighted Riemannian manifold withCD(0,N)condition.
Theorem 1.3LetMbe ann-dimensional compact weighted Riemannian manifold with theCD(0,N)condition.Suppose thatuis a smooth positive solution to(1.1)andvsatisfy equation(2.1)onM.Then for anyp>1,andκ(p(m+1)?1)>0,
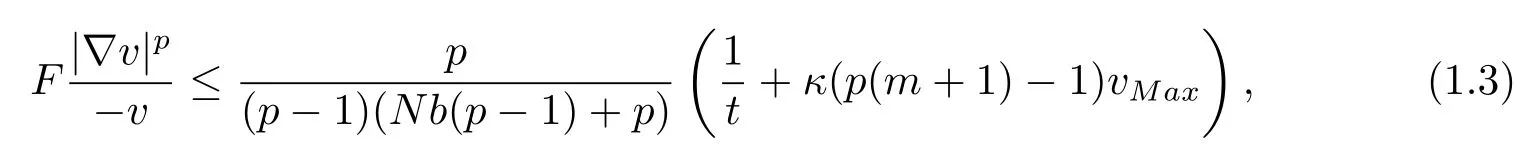
wherevMaxmaxMvm.
As applications of two estimates in Theorem 1.1 and 1.3,by integrating along minimizing geodesic paths,we can derive the corresponding Harnack inequalities.
Corollary 1.4LetMbe ann-dimensional compact weighted Riemannian manifold with theCD(0,N)condition,ube a positive solution to(1.1)andvsatisfy the equation(2.1).Given anyx1,x2∈M,0≤t1


Corollary 1.5LetMbe ann-dimensional compact weighted Riemannian manifold with theCD(0,N)condition,ube a positive solution to(1.1)andvsatisfy the equation(2.1).Given anyx1,x2∈M,we have:
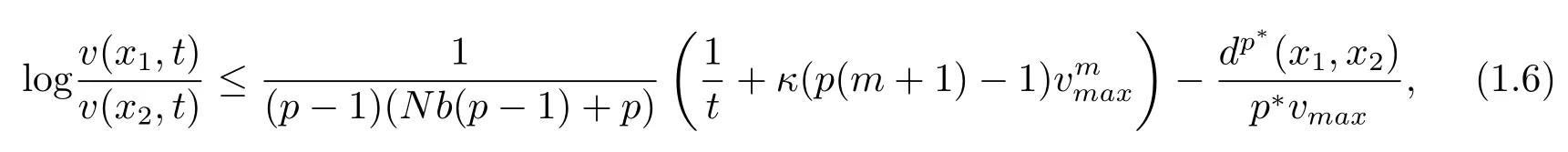
The organization of this paper is as follows.In Section 2,using the weightedp-Bochner formula,we will give the proof of Li-Yau type difference Harnack estimate(1.2).In section 3,we will prove Hamilton type estimate(1.3).In Section 4,two Harnack inequalities are derived as applications of two type estimates.
2 Global Li-Yau Type difference Harnack Estimate
In this paper,let?and div be the gradient operator and divergence operator onM.Assume thatuis a positive solution to(1.1),the pressure transform introduced by the first author in[6],
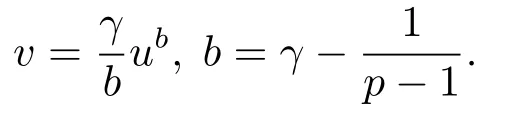
The WNRDE can be rewritten as
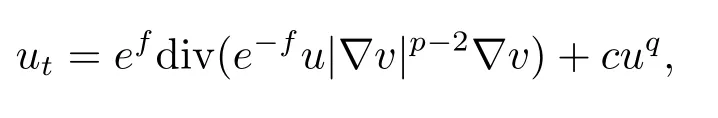
and corresponding pressure equation forvsatisfies
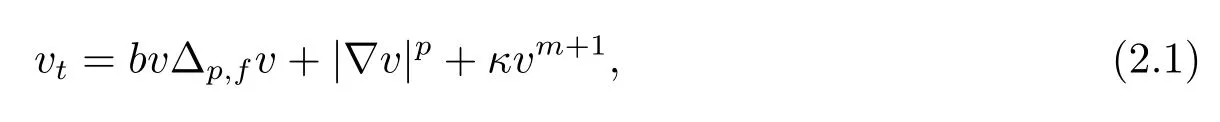
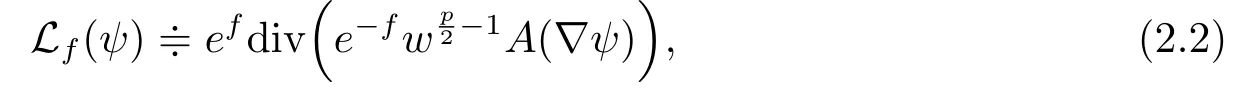
and its parabolic operator iswherew=|?v|2>0,and
Lemma 2.6Let

Then
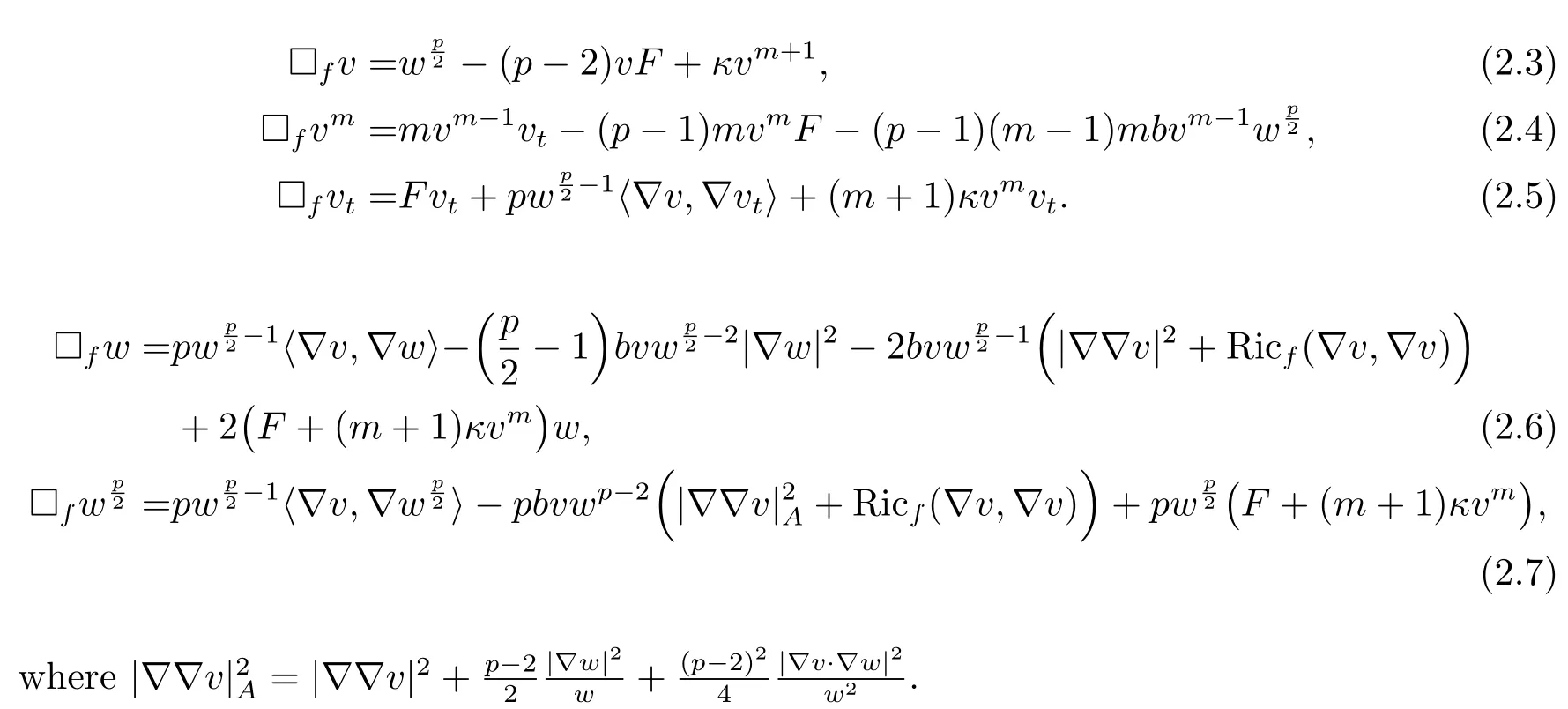
ProofFor a constantβ,combining the equation(2.1)and the definition ofLin(2.2),we have
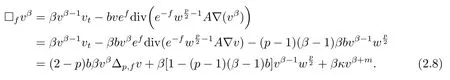


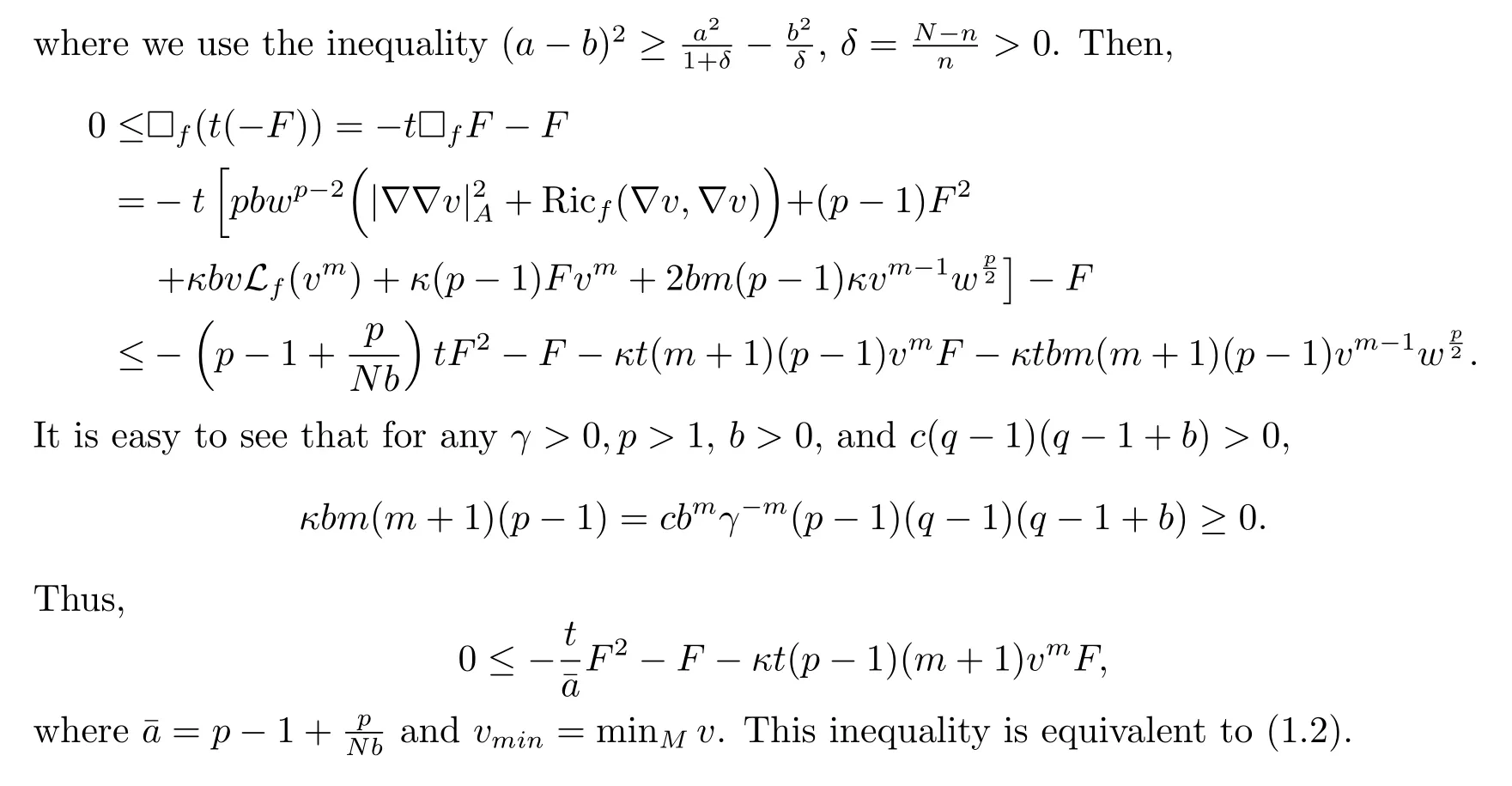
3 Global Hamilton Type difference Harnack Estimate
In this section,we establish a Hamilton type difference Harnack estimate for positive solutions to WNRDE(1.1)on weighted Riemannian manifolds.

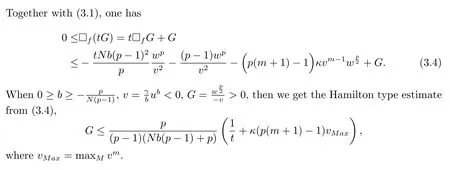
4 Applications of difference Harnack Estimates


