基于增維細胞傳輸模型的區域管制空域容量評估

高 偉， 康道馳

(中國民航大學空中交通管理學院， 天津 300300)

在中國民航近30年的持續高速發展過程中，經空域規劃與管制技術的不斷升級完善，北京、上海、西安等中國繁忙機場的終端區空域通行能力大幅提升，機場容量的運行瓶頸已逐漸轉移至終端區所在區域管制空域的接收能力。為了改善空域資源供給與利用，需要對區域管制空域的運行服務能力即區域容量進行評估。

涉及區域容量的研究主要分為空中交通流量管理、拓撲結構、交通流復雜度和危險天氣影響4個方面。

空中交通流量管理主要以延誤、安全成本與容量為目標對區域流量進行優化。Bayen[1]利用拉格朗日算法分析了航路容量和交通流延誤問題，并利用混合整數線性規劃(mixed integer linear programming，MILP)算法給出了優化后的方案，提出繁忙空域交通流量歐拉網絡模型和基于空中交通流量管理的拉格朗日延遲模型來計算區域容量。Chen等[2]基于動態空中交通流構建航路網絡模型，采用對偶分析法求解以運行花費最小作為目標函數，以區域容量作為限制條件的混合整數線性規劃問題，從而實現對區域交通流的優化。Hossain等[3]提出空域容量與安全風險折中計算模型，計算在可接受的安全風險下的區域扇區最大容量。

拓撲結構主要從航路網絡復雜度分析和航路網絡結構兩方面進行研究。網絡復雜度分析主要將航路網絡抽象為拓撲網絡，使用復雜網絡理論對航路網絡拓撲結構進行分析。描述復雜網絡的特征量主要包括度、權、平均路徑長度、簇系數、度分布、介數等。陳才龍[4]提出一種空域容量的多目標粒子群優化方法，通過復雜網絡建模，給出了空域容量的一種定量描述方法，最后采用多目標粒子群算法得到了航路匯聚點布局問題的非支配解。航路網絡基本結構的研究主要包括航路交叉點個數及位置、航段長度、航路交叉角度等與航路網絡容量間的關系。Wang等[5]在航路網研究的基礎上考慮了限制區、危險區、禁區的限制因素，通過對交叉點的合并與位置改變實現對航路網結構優化，并基于元胞自動機思想求解該模型。

交通流復雜度方面，Song等[6]提出了基于交通流模式識別的空域容量預測方法，考慮交通流屬性和管制員的管制策略因素，對未來30 min到幾小時內的空域動態容量進行預測，但并未探討交通模式與容量之間的關系，以及不同時間尺度內的交通流模式的預測方法。

危險天氣方面，Mitchell[7]研究了在確定的空域范圍和給定的惡劣天氣影響下的容量算法，并且分析了天氣對容量的影響；Krozel等[8]考慮惡劣天氣和各種運行條件進行了航路容量評估。

現基于區域航路網絡拓撲結構對研究區域容量采用細胞傳輸模型將區域航路網中每條航線分為若干細胞，將時間離散化為若干時段，以細胞容量作為限制條件，以容量最大作為目標函數構建MILP模型，通過遺傳算法對該模型進行求解。通過與TAAM仿真軟件的對比來驗證該模型的準確性。

1 細胞傳輸模型

1.1 細胞傳輸模型概述

細胞傳輸模型(cell transmission model，CTM)是運動學模型LWR(lighthill，whitham and richards)模型差分離散形式[9]。經過十幾年來的發展，中外不少學者對其進行了進一步研究和完善，CTM 已經成為模擬路網中的動態交通流傳播，研究交通流運行規律的有效工具。將細胞傳輸模型引入空中交通，并對其進行增維處理，加入高度維對區域空域網絡進行建模。

1.2 定義

圖1所示為區域航路航線網絡圖，區域航線網絡分為若干高度層，每一高度層上的二維航線網絡由航線、區域邊界和航路點構成。

1.2.1 點

點包括轉彎點、航線與航線的交叉點及區域邊界與航線的交點，用P表示。在圖1中共有10個點則P={P1,P2,…，P10},其中P2、P6表示轉彎點；P3、P9表示航線交叉點；P1、P4、P5、P7、P8、P10表示區域邊界與航線的交點。

1.2.2 邊

邊分為航段與區域邊界線。航段為航線上兩點之間的部分用L表示。在圖1中共有9個航段則L={L1,2,L2,3,L3,4,,L8,9,L9,10,L5,9L9,6L6,3,L3,7}。以L1,2為例表示點P1與點P2之間的航線部分，其方向為從點P1到點P2，航段方向與所在航線方向一致。航線由航段組成，用R表示，航線分為經由區域進出終端區的航線和通過區域空域但不經過終端區的飛越航線兩類。在圖1中共有3條航線，R={R1,R2,R3}。其中以航線R1為例，航線R1由航段L1,2、L2,3、L3,4組成，R1={L1,2,L2,3,L3,4}，其方向為P1→P2→P3→P4。區域邊界為所選定區域空域的邊界線在圖1中以粗實線表示。

1.2.3 高度層

區域管制空域為三維空間，分為若干高度層，每個高度層上的二維航線網絡均相同。高度用H表示，圖1中共有3個高度層，H={H1,H2,H3}。

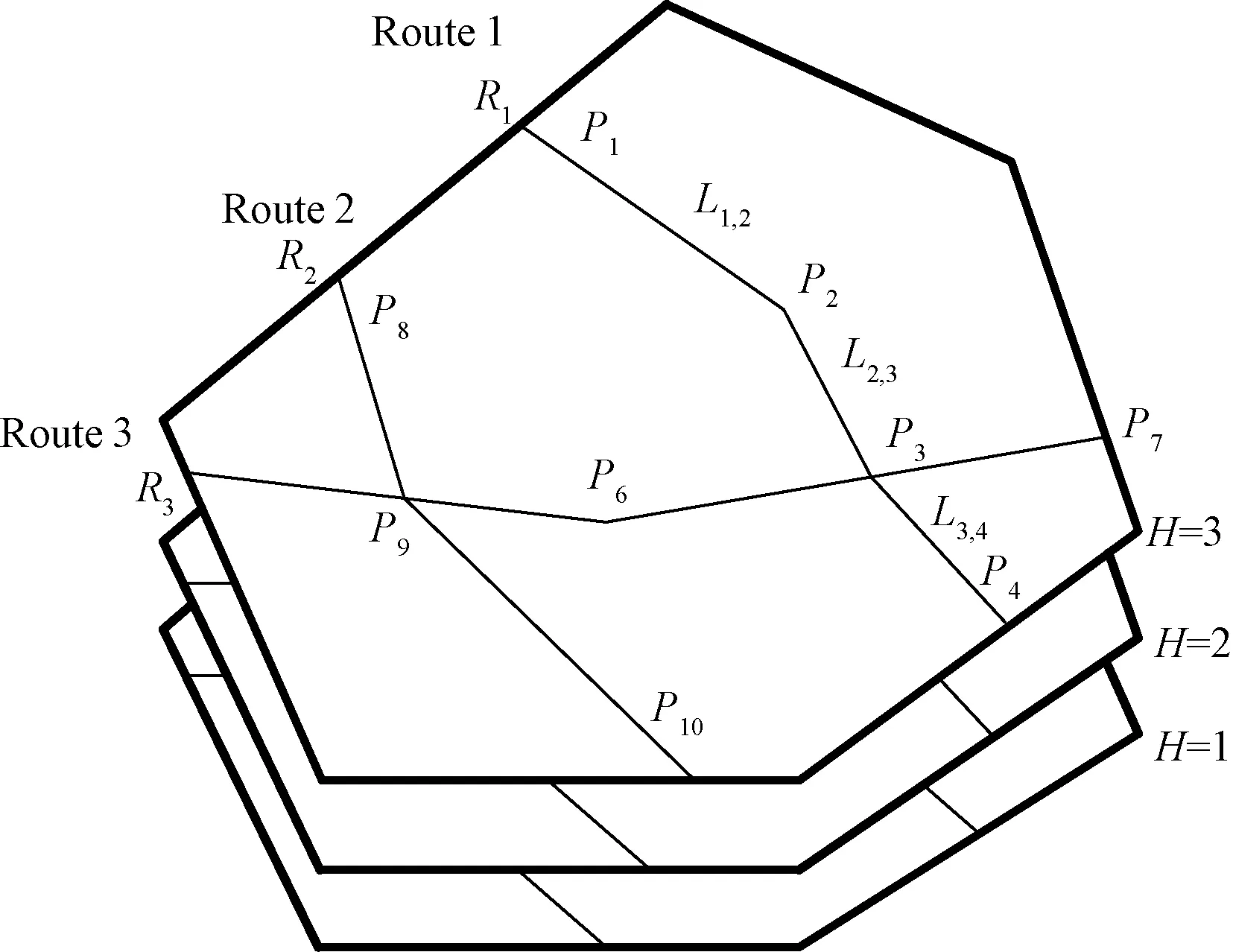
圖1 區域空域航線網絡圖Fig.1 Regional airspace route network diagram

1.2.4 細胞

將每個航段按區域管制間隔分為若干細胞，用C表示。細胞作為組成航線網絡的最基本單元C={C1,C2，…，CN}，N表示航線網絡中細胞的總個數。圖2以航段L1,2為例將航段L1,2分為n個細胞每個細胞長度為區域管制間隔。由于航段長度與區域管制間隔并非整數對應關系，所以要對每個航段的最后一個細胞長度進行取整保留。

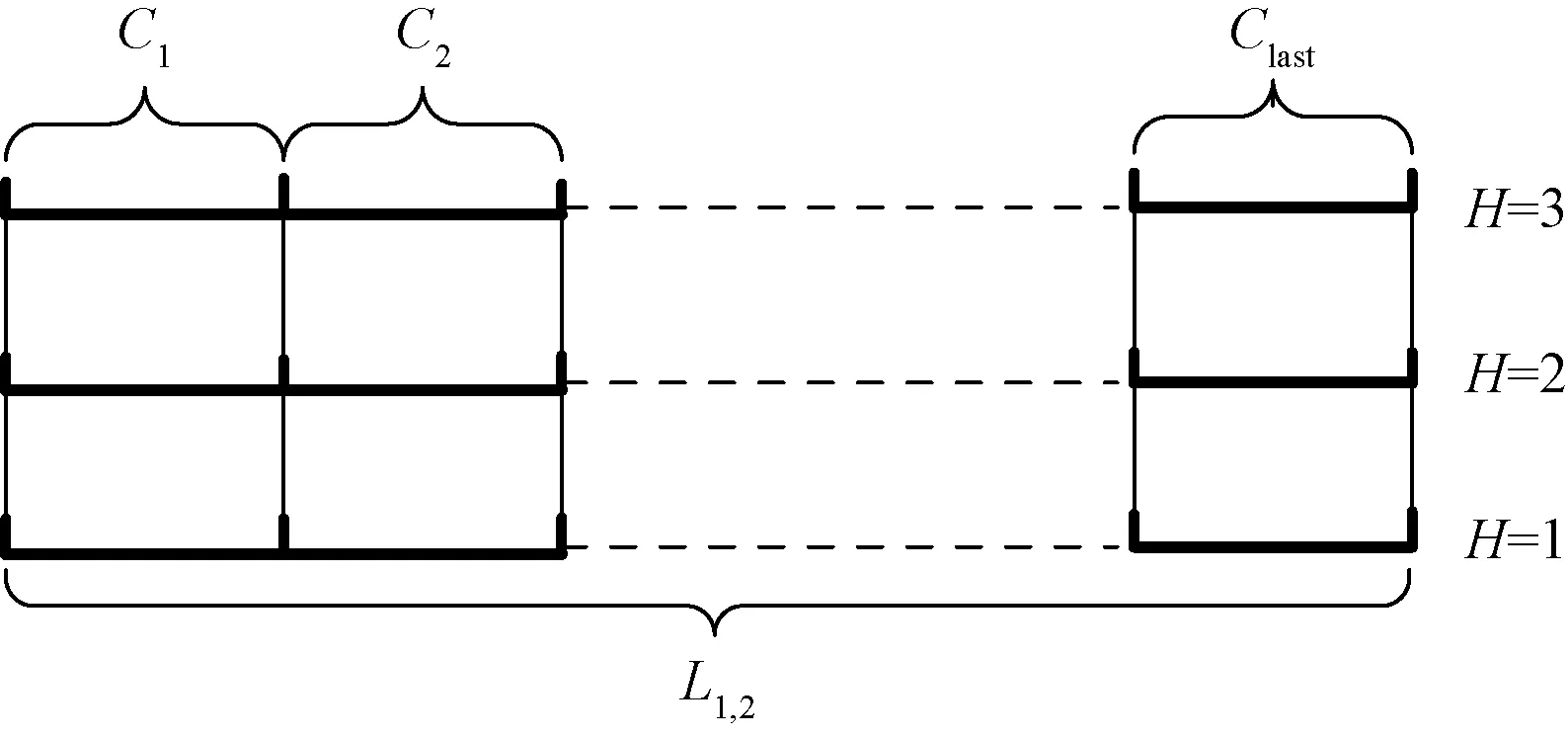
圖2 航線細胞結構圖Fig.2 Diagram of route cell structure

(1)

式(1)中：n表示航段L1,2上細胞的個數；DL1,2表示航段L1,2的長度；Dcontrol表示區域管制間隔。

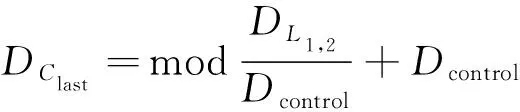
(2)

式(2)中：Clast表示位于航段L1,2上最后的細胞，其中Clast∈{C1,C2，…，CN}；DClast表示細胞Clast的長度。

(3)

式(1)中的n為四舍五入后的取整值，當航段長度與區域管制間隔相除的小數部分小于0.5時，航段上最后一個細胞Clast的長度如式(2)所示，反之取式(3)。每個高度層上的細胞分布均相同。

1.3 飛行速度分析

根據雷達數據分析，影響航空器飛行速度的主要因素為高度層與航段位置。如圖3所示，通過對同航段不同高度層上的航空器速度分布進行對比，航空器速度每個高度層上呈正態分布，但高度層不同，速度的均值與方差也不同。如圖4所示，在相同高度層的不同航段上航空器的速度分布依然呈正態分布，航段不同，正態分布的參數也不同。

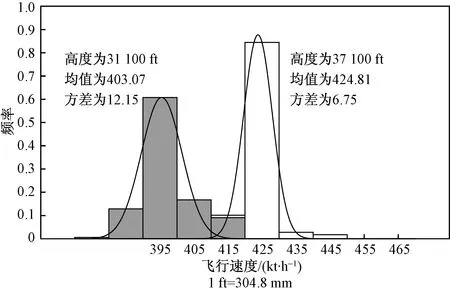
圖3 不同高度層速度分布Fig.3 Velocity distribution at different levels

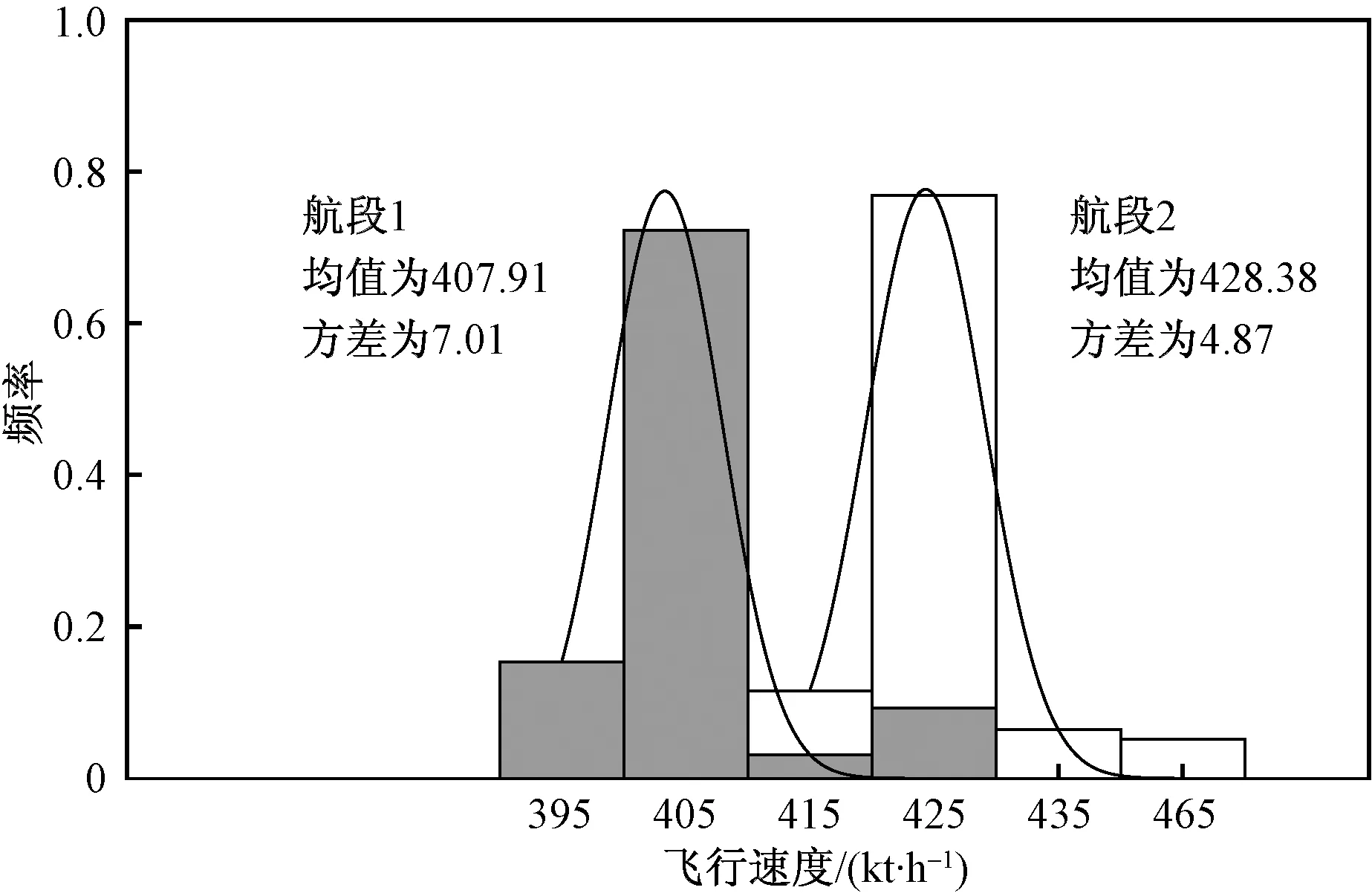
圖4 不同航段速度分布Fig.4 Velocity distribution of different sections

通過以上分析可知，航空器的飛行速度在各航段各高度層上均呈正態分布，即各航段各高度層上航空器的飛行速度大部分落于某一速度區間之內，以正態分布的均值作為航空器的飛行速度，不會造成過大的計算誤差，滿足精度的要求。由于正太分布均值與方差隨高度層和航段位置的變化而變化，速度變量將由航空器所在細胞的航段位置及高度所決定。

1.4 細胞傳輸模型構建

1.4.1 模型假設

(1)航空器在細胞內的飛行速度為恒定值，速度由細胞所在航段位置及高度決定。

(2)將時間離散化，以分鐘作為時間單元進行計算。

(3)模型不考慮天氣等隨機因素的影響。

(4)區域飛越航線以平飛為主不發生高度層的改變，進出終端區航線會發生高度層的改變。

(5)航空器需要改變高度層時，航空器從細胞的起始端開始高度變化在完成一個高度層跨越時其飛行的水平距離為一個細胞的長度，如圖5所示。航空器在改變高度時其水平速度取該細胞所在兩個高度層速度的平均值。航空器不在交叉點處發生高度層改變。

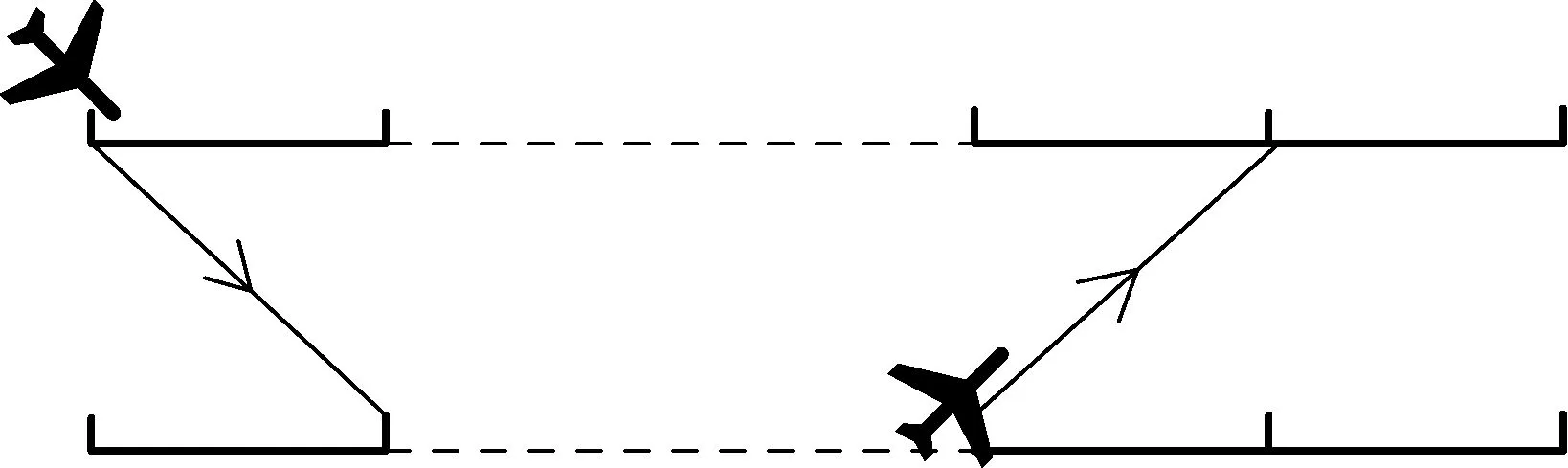
圖5 航空器高度層改變示意Fig.5 Elevation level change of aircraft

1.4.2 模型變量計算

1.4.2.1 飛越細胞時間

航空器飛越細胞所用時間由細胞所在航段位置及高度層決定。

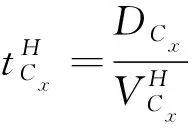
(4)

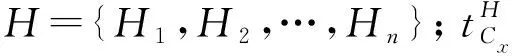
1.4.2.2 進入區域交通流

以1 min為時間單元對進入區域的航空器進行標定。

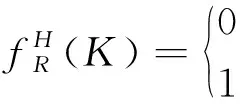
(5)

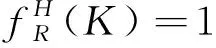
1.4.2.3 高度層

每一架航空器都將生成一個高度層矩陣，高度層矩陣表示航空器在航線的每個細胞上飛行所使用的高度層。高度層矩陣的維度為高度層數×航線細胞數。

(6)

1.4.2.4 進入細胞時間

當式(5)的值為1時航空器進入細胞時間取決于細胞所在位置及進入區域空域時間。

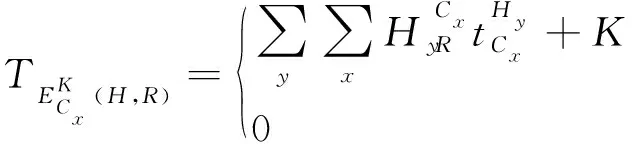
(7)

式(6)中高度矩陣為0的元素進入時間均為0，表示航空器不從該高度層進入該細胞。

1.4.2.5 離開細胞時間

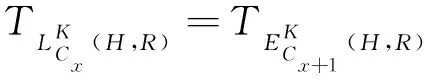
(8)

1.4.2.6 交叉點間隔

交叉航線可以看作由多個轉彎航線構成，求解交叉點間隔則轉化為求解轉彎點間隔。轉彎點示意圖如圖6所示。航空器F1到達轉彎點P1時航空器F2距航空器F1的距離記為d。當航空器F1通過點P1時兩航空器之間的距離可以表示為

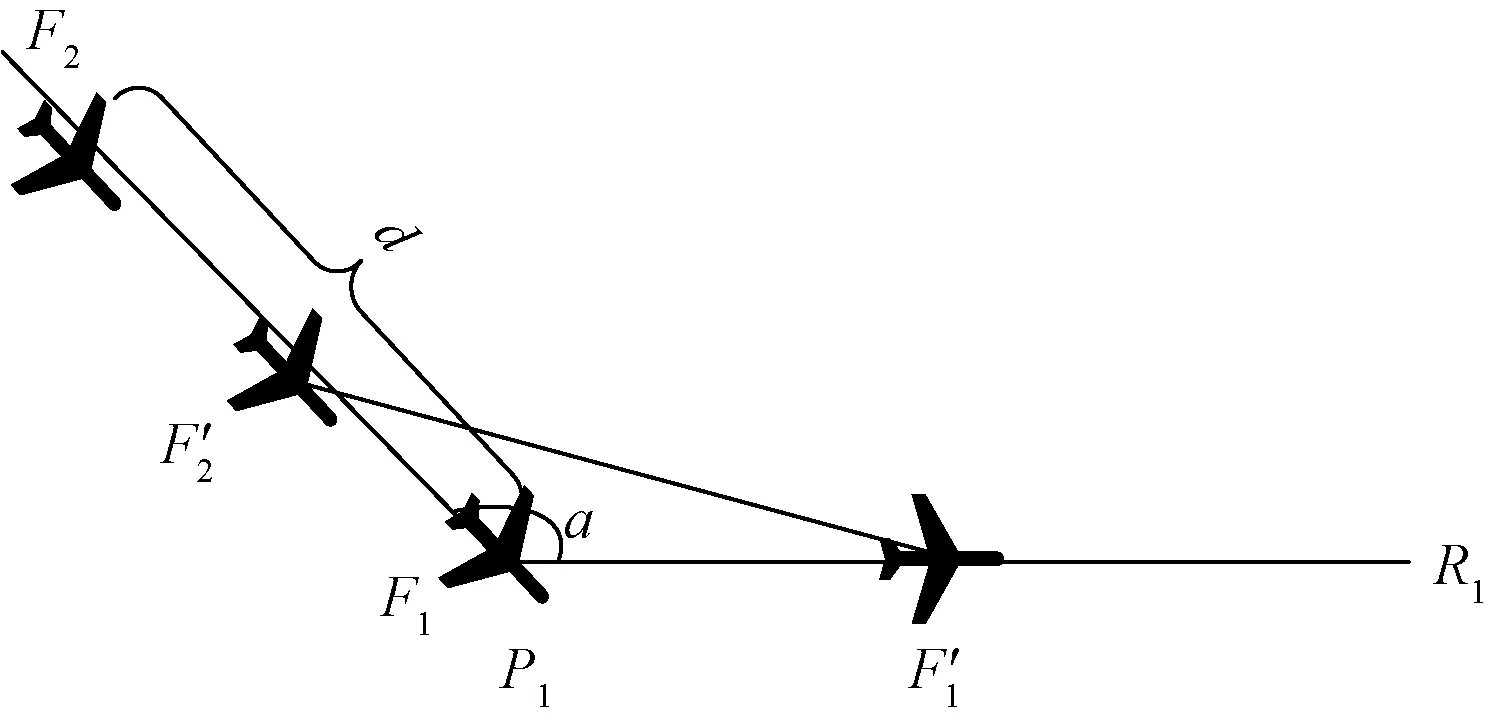
圖6 轉彎航線示意圖Fig.6 Diagram of turning course

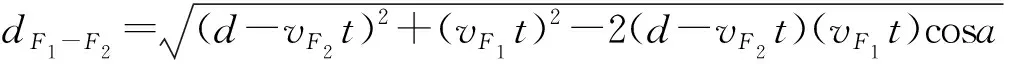
(9)

式(9)中：dF1-F2表示航空器飛過P1點后兩航空器之間的距離；時間t以航空器到達點P1時記作0；a為兩航段的夾角；vF1、vF2為兩航空器速度，其數值等于航空器所在細胞的速度。

通過對式(9)求導求解兩航空器之間的最小值，令最小值等于區域管制間隔。通過對導數為零與最小值等于區域管制間隔兩式聯立解出d。

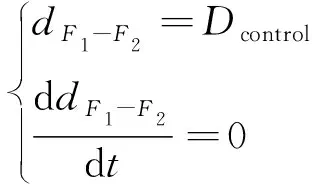
(10)

過點P1的時間間隔為

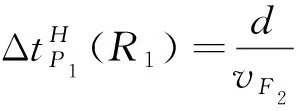
(11)

交叉航線可以看作由多個轉彎航線構成(圖7)，其中交叉航線由n×n種轉彎航線組合而成則交叉點間隔取轉彎點間隔的最大值，如式(12)所示。

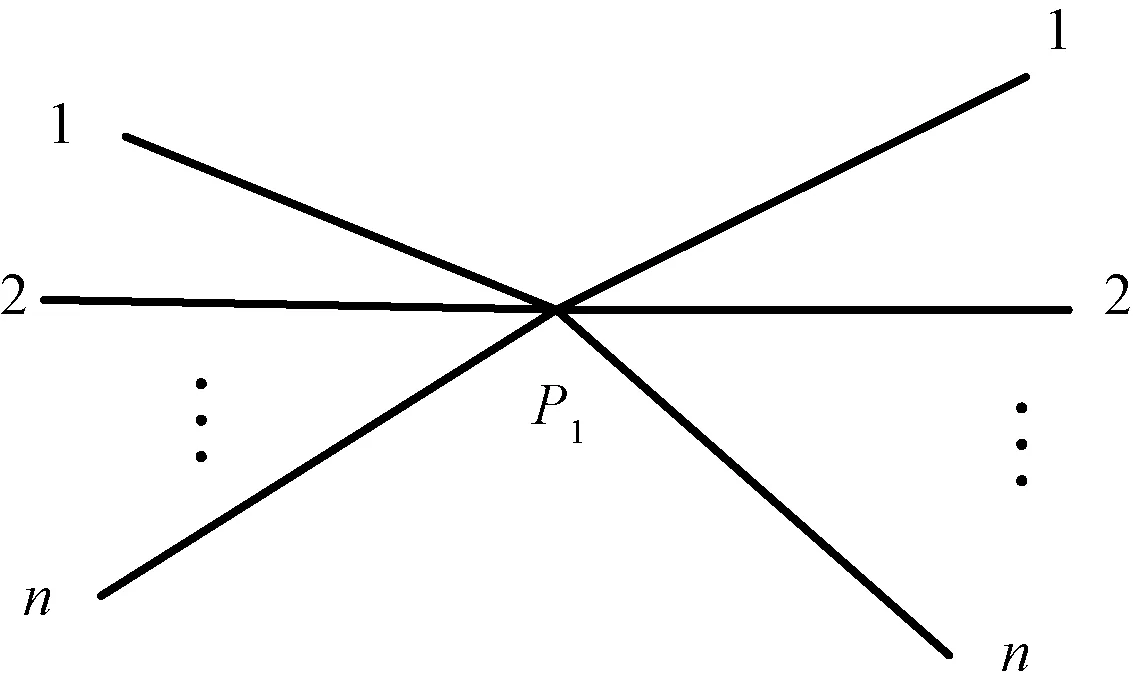
圖7 交叉航線示意圖Fig.7 Diagram of crossing route

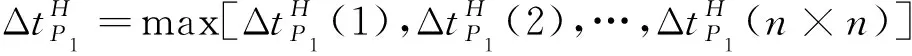
(12)

1.4.2.7 細胞通過量

1.4.2.8 扇區通過量

扇區作為區域空域的組成部分，將扇區通過量定義為給定時間內通過扇區的航空器數量，用Sx表示。

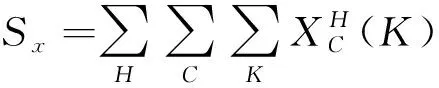
(13)

式(13)中：Sx表示給定時間內通過扇區x的航空器數；C表示扇區入口處細胞的集合；K為給定時間集合；H為高度層集合。

1.4.2.9 區域通過量

區域通過量與扇區通過量類似，表示給定時間內航空器通過區域空域的數量，用A來表示。

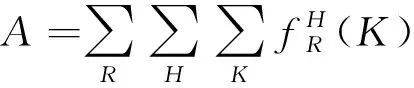
(14)

1.4.3 區域容量

由于以求解區域最大容量為目的，所以目標函數為一定時間內進入區域航空器數量最大。限制條件為細胞容量與交叉點間隔。由于細胞長度為區域管制間隔，所以所有細胞容量均為1。

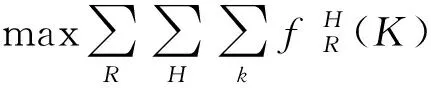
(15)

限制條件：

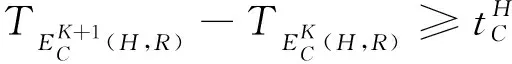
(16)

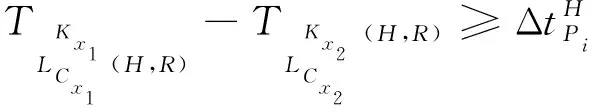
(17)

式(17)中：Pi為航路交叉點的總集合；Cx1、Cx2表示以交叉點Pi為細胞終點的細胞集合；Kx1、Kx2分別表示細胞Cx1、Cx2進入區域空域的時間。

式(16)表示相鄰兩架航空器后機進入細胞C前機進入細胞C的時間差大于細胞C的通過時間確保了細胞C的容量為1；式(17)則表示通過交叉點的時間差大于允許值。

2 遺傳算法求解

2.1 遺傳算法概述

遺傳算法是模擬達爾文遺傳選擇和自然淘汰生物進化過程的計算模型[10]。該算法是一種基于生物自然選擇與遺傳機理的隨機搜索算法，起源于對生物系統進行的計算機模擬研究，是自然遺傳學和計算機科學相互結合滲透而成的算法。

與傳統搜索算法不同，遺傳算法[10-11]從一組隨機產生的初始解開始搜索過程，該初始解稱為種群(population)。種群中的每個個體是問題的一個解，每個個體由攜帶基因編碼的“染色體”組成。遺傳算法通過對初始種群的選擇、交叉、變異運算篩選出最優個體，即為所求的最優解。

2.2 遺傳算法構建

2.2.1 初始種群生成

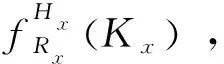
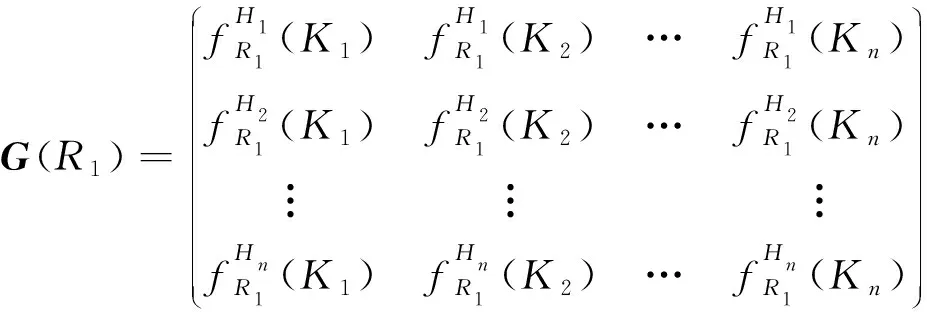
(18)

式(18)中：G(R1)表示個體中航線R1基因序列，矩陣G(R1)中的每一行為個體的一個染色體，染色體的長度為給定時間段的長度Kn。

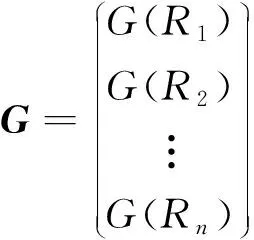
(19)

式(19)中：G表示個體的基因序列由區域空域中的每一條航線的基因序列組成。

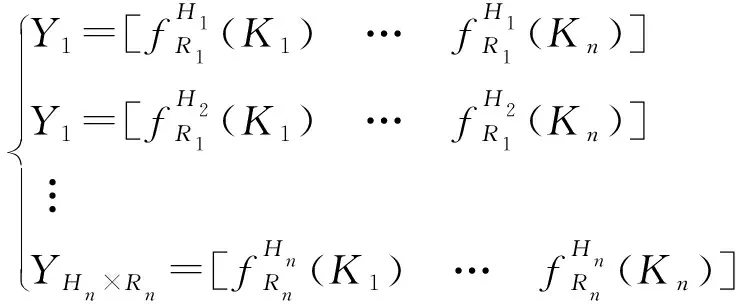
(20)

式(20)中：Y表示染色體。

個體中的染色體Y的數目為矩陣G的行數，即Hn×Rn。對生成個體進行檢驗使生成的個體需要滿足式(16)、式(17)的限制條件，生成多個滿足條件的個體構成初始種群。

2.2.2 適應度

適應度是在研究自然界中生物的遺傳和進化現象時，用來度量某個物種對于生存環境的適應程度。對生存環境適應度較高的物種將獲得更多的繁殖機會,而對生存環境適應程度較低的物種，其繁殖機會就會相對較少，甚至逐漸滅絕。本文中個體以給定時間內進入區域空域航班數的總和為適應度，如式(21)所示。

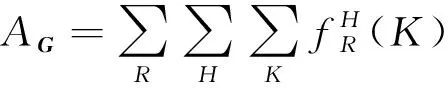
(21)

式(21)中：AG表示個體G的適應度。

2.2.3 選擇

選擇指決定以一定的概率從種群中選擇若干個體的操作。一般而言，選擇的過程是一種基于適應度的優勝劣汰的過程，本文中選擇過程將采用基于適應度選擇的輪盤賭算法，即適應度越大選擇概率越高，原理類似于博彩游戲中的輪盤賭。個體選擇概率為

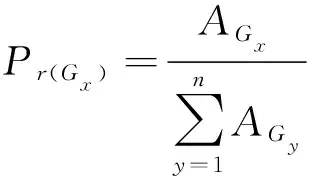
(22)

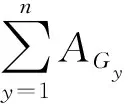
2.2.4 交叉

有性生殖生物在繁殖下一代時2個同源染色體之間通過交叉而重組，即在2個染色體的某一相同位置處DNA被切斷，兩染色體互相交換被分離的染色體片段后組成新的染色體。本文中采用單點交叉，由于單個染色體的長度為給定時間段的長度，所以交叉點的選取范圍為(2,Kn-1)。圖8所示為個體G1與個體G2的Y1進行交叉重組。

圖8 染色體交叉示意圖Fig.8 Diagram of chromosome crossing

2.2.5 變異

變異指染色體復制時可能(很小的概率)產生某些復制差錯，變異產生新的染色體，表現出新的性狀。本文中則表示個體中染色體上為0的基因以一定概率突變成1。

2.2.6 遺傳算法總流程

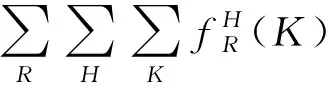
3 算例

選取覆蓋北京終端區的12個區域扇區作為研究對象，如圖10所示，共有80個航路點、184個航段、636個細胞和153條航線其中134條通過區域航線，10條由區域進入終端區航線，9條從終端區進入區域航線。北京區域扇區的管制高度為7 800～12 500 m，按照東單西雙原則向東的航線分為8 100、8 900、9 500、10 100、10 700、11 300、11 900、12 500 m共8個高度層，向西的航線分為7 800、8 400、9 200、9 800、10 400、11 000、11 600、12 200 m共8個高度層。

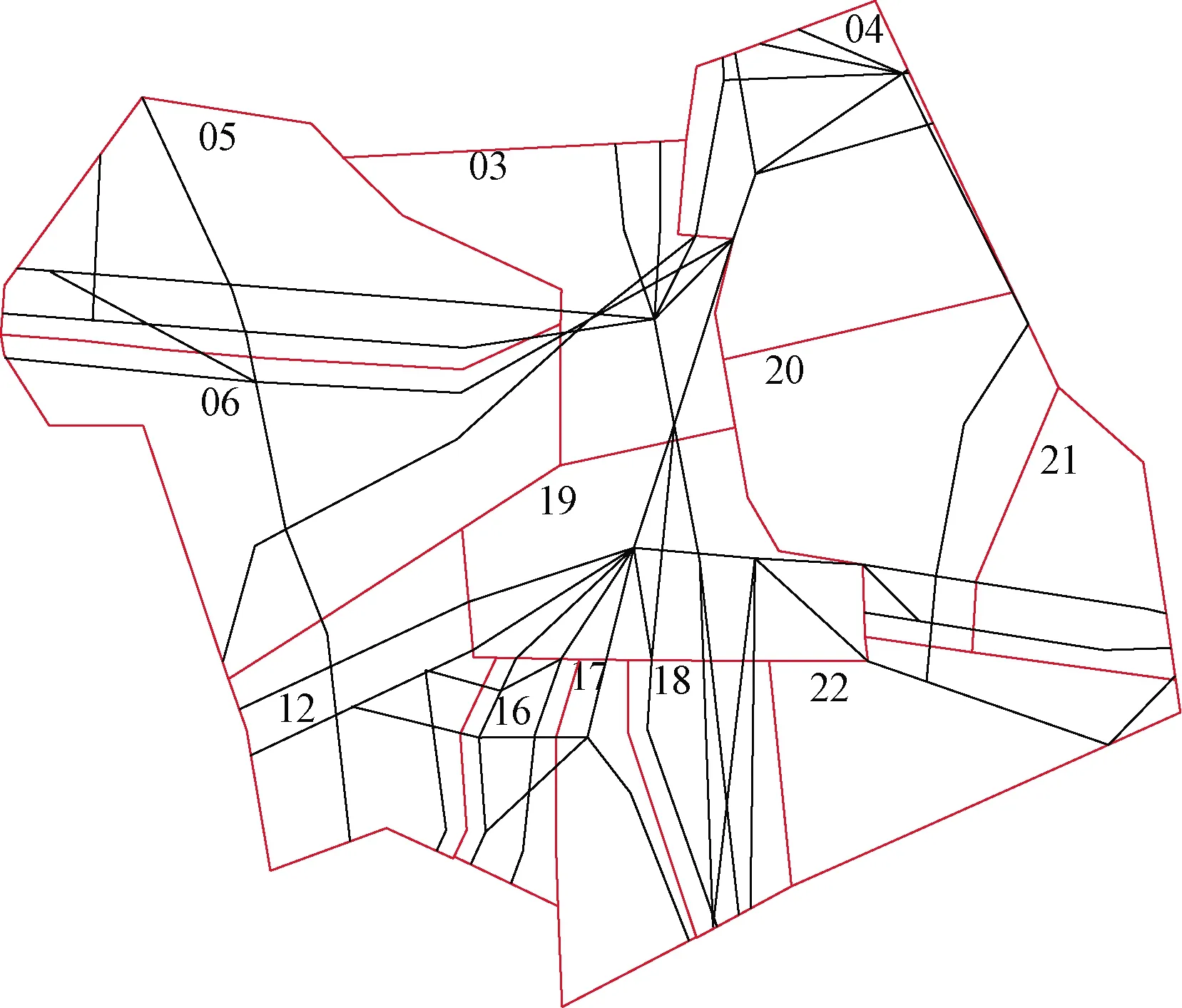
圖10 選取區域空域示意圖Fig.10 Diagram of selected regional airspace

3.1 計算結果

選取1 h為總時長，計算區域空域1 h的最大容量。所需參數：區域管制間隔為20 km，初始種群中的個體數為100交叉概率0.6，變異概率0.01。遺傳算法經50次迭代后結果如圖11所示。最終收斂的均值為884.52，即選定區域空域的小時容量為884架次。進入終端區和從終端區進入區域空域的小時架次116.54，通過區域空域的小時架次為767.98。

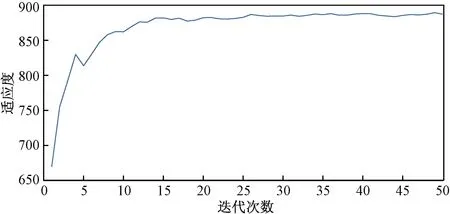
圖11 適應度迭代曲線Fig.11 Fitness iteration curve

3.2 TAAM仿真驗證

選擇收斂后群體的一個個體作為樣本生成時刻表，通過TAAM對該時刻表的仿真與CTM模型計算結果進行對比。表1為各扇區小時通過架次的比較，可以看出，交通流主要集中在12扇區、16扇區、17扇區和19扇區，總體上計算值要略高于仿真值。

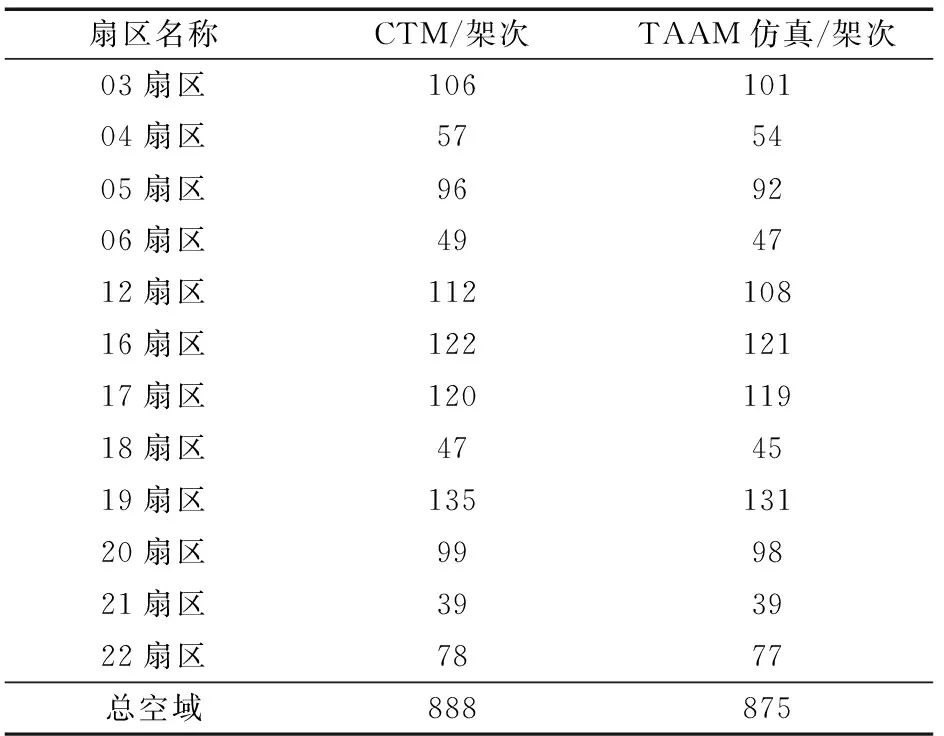
表1 扇區小時通過架次統計Table 1 Sector hour statistics

4 結論

采用增維細胞傳輸模型構建區域交通流MILP模型，利用遺傳算法進行求解得到區域空域容量，取得了與TAAM基本一致的結果。這說明CTM適合區域交通流這種中觀尺度的空域容量分析，且不需要購置昂貴的仿真平臺，建模簡單，只要給定區域空域結構，即可快速分析其容量，有助于分析區域空域對終端區進入區域航班的接收能力，從而對合理分析與規劃機場容量提供重要決策依據。該模型只要將有關場景涉及的細胞部分稍作處理，還可以得到災害性氣象條件或軍事活動影響下的區域管制空域容量。