反思促成長

周東

摘要：問題是數學的心臟，是教學的核心。初中數學教師在解題教學中，如果沒有題后反思，數學思維就會停滯不前，要培養學生的解題能力，就要和學生一起反思，養成題后反思的習慣。筆者認為，一要反思學生思維的受挫點，彌補知識的漏洞；二要反思解題路徑，尋求一題多解；三要反思題目的不變性，研究解題規律；四要反思一題多變，提高思維的變通性。

關鍵詞：解題規律；解題能力；教學反思

中圖分類號：G633.6文獻標識碼：A文章編號：1992-7711（2020）06-0069

案例：某數學課分析試題，如圖直角三角形ABC，∠ABC=90°，AB=6，BC=3，將△ABC沿著斜邊AC對折，點B落在點B′處，過B′作BD垂直于直線AB，D為垂足，求CD的長。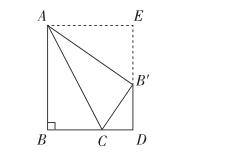

分析：本題利用對折即軸對稱的性質，可以得出∠AB′C等于90°，可以利用直角三角形B′CD勾股定理來列方程求解。但是CD、B′D的長度是未知的，如何找到這兩條邊的關系成了解決這個問題的關鍵。根據∠AB′C=90度，可以聯想到K型圖，向外補形就可以得到△CDB′和△BEA相似。相似比為1∶2，可以設CD=X，則B′E=2X，B′D=6-2X，由勾股定理就可以列方程x2+（6-2x）2=32求解即可。

此時下課鈴響起，為了不拖堂，筆者就說這個圖還有什么規律，請大家課后再去研究。課后一個姓吳的學生找到筆者說：“老師我發現△CDB′的三邊之比為3∶4∶5。”筆者當時一愣，這個可是筆者本人都沒發現的規律。“真的嗎？”筆者說，結果一算真的是這樣，就是這樣一個三邊關系，然后我們就一起把這規律寫成“如圖，當BC∶AB=1∶2時，沿著AC折疊得到直角三角形B′CD的三邊之比為3∶4∶5”，而筆者就把這個定理命名為“吳氏定理”，這時這位吳同學甭提有多高興了。

又過了一天，吳同學又把他的定理擴充了“如圖，當BC∶AB=1∶3時，沿著AC折疊得到直角三角形B′CD的三邊之比也是3∶4∶5，”“相同嗎？”筆者問，“一個是橫∶豎∶斜=3∶4∶5，另一個是豎∶橫∶斜= 3∶4∶5”。

“厲害，不愧為我們班的數學天才！”筆者及時給予肯定，激發了他更多的數學熱情。此后，在平時的教學中我們又多了一個“吳氏定理”的應用。從此以后這位吳同學學習數學的積極性空前高漲，最后以優異的成績提前被重點中學錄取。

初中數學教師很多時間都花在解題上。但是題目千變萬化，即使做得再多也不可能做完。數學家曾說過，數學問題的解決僅僅只是一半，更重要的是解題之后的回顧。一道數學題經過一番冥思苦想解出答案后，如果不進行反思，那么只會做這一題，跟學生講，學生最多也是明白這個題目。進行認真反思梳理，研究規律，發現不變性，可以點撥解題思想方法，大大提高學生的解題能力，達到做一題會一類的效果。那么，教師如何反思？反思什么呢？

一、反思學生思維的受挫點，彌補知識的漏洞

在問題解決之后，反思解題過程是否遺漏已知條件或隱含的條件？解題過程多走了哪些思維回路？是否拘泥于思維定式，照搬了熟悉的解法？通過這樣不斷地質疑、不斷改進，讓解題過程更具有合理性、科學性、簡捷性。

1.學生對K型圖的理解不深刻，認為△ABC和△CDB′是一個K型圖相似，求出了錯誤的答案。這里∠ACB′和∠ABC、∠CDB是不相等的，因此這兩個三角形是不能證明相似的，我們應該加強一線三等角本質特征的認識，加深對相似判定的理解。

2.用勾股定理列方程出錯，不能找出CD和DB′的關系。

3.數學思想方法的欠缺，找不到問題的出發點。這就要加強學生分析問題能力的培養。

二、反思解題路徑，尋求一題多解

在問題解決之后，反思能否開辟新的解題通道？解題過程思維、運算能否變得簡捷？通過這樣不斷質疑、不斷改進，尋找一題多解的方法，從而提高思維的廣度。

通過反思，此題建立了“對折——全等——勾股定理列方程求解，補形——一線三等角——相似表示未知的兩邊”這樣一個解題思路，形成一定的解題方法。

2.把直角對折，若求邊長，常設未知數，找到直角三角形利用勾股定理、方程思想可以解決。

3.角平分線+平行必有等腰三角形、K型圖相似、勾股定理列方程等思想方法，向外補形和向內分割的添加輔助線的方法。

四、反思一題多變，提高思維的變通性

解題之后反思把這個題目放在矩形中就可以變式出很多的題目，通過變式的練習，不斷地探究問題的知識結構和系統性。能否對問題蘊含的知識進行縱向深入地探究？能否加強知識的橫向聯系？把問題所蘊含孤立的知識“點”，擴展到系統的知識“面”，通過不斷地拓展、聯系、加強對知識結構的理解，進而形成認知結構中知識的系統性，提高學生思維的變通性，提高解題的能力。

例如：在矩形ABCD中，AB=6，BC=8，點E是BC上的一動點，把△ABE沿AE折疊。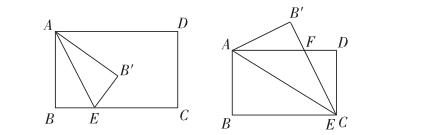

1.若B點對應點B′恰好落在∠BCD的平分線上，求B′C。

2.若B點對應點B′恰好落在矩形的對稱軸上，求BE。

3.若點E落在點C處，B′E和AD相交于點F，求△AFE的面積。

……

總之，問題與問題之間不是孤立的，許多表面上看似無關的問題卻有著內在的聯系、共性的知識、不變的規律、相同的思想方法，解題不能就題論題，要題后反思，構建知識網絡，提煉數學思想、數學方從而提升解題能力，讓學生脫離題海。

（作者單位：浙江省金華市武義縣實驗中學321200）