經(jīng)歷探究過程，把握面積本質(zhì)

蘭贈連

學(xué)過長方形的面積計算公式后，對于公式中的“長”“寬”分別表示什么的問題，有相當(dāng)多的學(xué)生都只能寫出其表面看得見的長度數(shù)量，而想不到背后所隱含的與面積有關(guān)的實質(zhì)意義。究其原因主要是教師教學(xué)中重結(jié)果輕過程。因此，在“長方形、正方形面積的計算”教學(xué)中，教師要突破現(xiàn)有教材內(nèi)容的局限，選擇合適的學(xué)具，讓學(xué)生親自參與測量、畫圖、觀察、思考、表達(dá)等學(xué)習(xí)活動，進(jìn)而真正理解面積計算公式。

面積的本質(zhì)是什么？為什么面積的單位名稱要加“平方”兩字？“長方形、正方形面積的計算”教學(xué)僅僅讓學(xué)生記住其計算公式就可以嗎？要回答諸如此類問題，我們首先要了解“長方形、正方形面積的計算”的教學(xué)現(xiàn)狀。

一、忽視面積本質(zhì)教學(xué)現(xiàn)狀一瞥

最近，筆者借助“停課不停學(xué)”期間建立班級學(xué)習(xí)群，對某校四年級某班學(xué)生進(jìn)行關(guān)于長方形面積本質(zhì)學(xué)習(xí)成效的網(wǎng)上調(diào)研。筆者要求學(xué)生計算長10厘米、寬6厘米的長方形的面積，并寫出算式中每個數(shù)表示的意義。該班參與答題的有42名學(xué)生，其中1名學(xué)生計算的是周長而不是面積，因而其對各數(shù)意義的表述也是錯的。41名學(xué)生計算長方形的面積及寫出算式中“60”的意義都是正確的，但是對算式中“10”“6”的意義卻只有4名學(xué)生寫對，另外37名學(xué)生都是將它們分別寫成表面上看得見的具體長度——“10厘米”“6厘米”（如圖1），沒有寫出背后所隱含的與面積有關(guān)的實質(zhì)意義。究其原因，一方面可能與學(xué)生對知識的遺忘有關(guān);另一方面更有可能與三年級下學(xué)期教師在教學(xué)“長方形面積的計算”時重結(jié)果輕過程有關(guān)。

在一次“送培下鄉(xiāng)”活動中，筆者執(zhí)教了“長方形、正方形面積的計算”一課，突破現(xiàn)有教材內(nèi)容的局限，選擇合適的學(xué)具，讓學(xué)生親自參與測量、畫圖、觀察、思考、表達(dá)等學(xué)習(xí)活動，經(jīng)歷探究過程，把握面積本質(zhì)，進(jìn)而真正理解面積計算公式。下面筆者就結(jié)合這次教學(xué)實踐談?wù)勛约旱淖龇ê退伎肌?/p>

二、對教材內(nèi)容的解析與思考

在教學(xué)人教版數(shù)學(xué)三年級下冊“長方形、正方形面積的計算”的例4時，教師安排了3個層次的內(nèi)容：1.用畫格子或用1平方厘米的正方形測量長5厘米、寬3厘米的長方形的面積;2.用1平方厘米的正方形拼擺多個長方形，并用表格記錄長方形的長、寬和面積，據(jù)此發(fā)現(xiàn)長方形的面積與長和寬的關(guān)系，進(jìn)而概括出長方形的面積公式;3.量出兩個長方形的長和寬，再計算面積。因第2個長方形的長與寬相等，根據(jù)正方形和長方形之間的關(guān)系，推導(dǎo)出正方形的面積公式。

首先，該例題只出現(xiàn)“平方厘米”這一種面積單位，沒有呈現(xiàn)學(xué)生已學(xué)過的所有面積單位。其次，在教學(xué)中教師如果讓學(xué)生完成例題中第1、2層次的測量、拼擺活動存在3個難點：一是學(xué)具備齊難。所有的文具店都沒有1平方厘米大小的正方形，只好用硬紙板剪，結(jié)果既剪不標(biāo)準(zhǔn)，又因數(shù)量太多（一組至少要15個），工作量大，耗時長。二是學(xué)生操作難。用硬紙板剪的1平方厘米的正方形小且輕，學(xué)生操作起來很困難，既難以做到無縫密鋪，又?jǐn)D占有限的課堂教學(xué)時間。三是同桌或小組合作難。因要測量的長方形小，測量工具也小，既不便于同桌合作，更不便于四人小組合作。因此，筆者只好另想其他方法，第1層次的測量活動改成用6個1平方分米的正方形測量長是3分米、寬是2分米的長方形的面積。這樣學(xué)具易準(zhǔn)備，學(xué)生也易操作。在方格圖上畫長方形的活動代替第2層次的拼擺活動，并增加用面積測量器（透明塑料上印有1平方厘米的方格圖）測量長方形面積的活動。

三、經(jīng)歷探究過程? 把握面積本質(zhì)

（一）巧用故事留伏筆

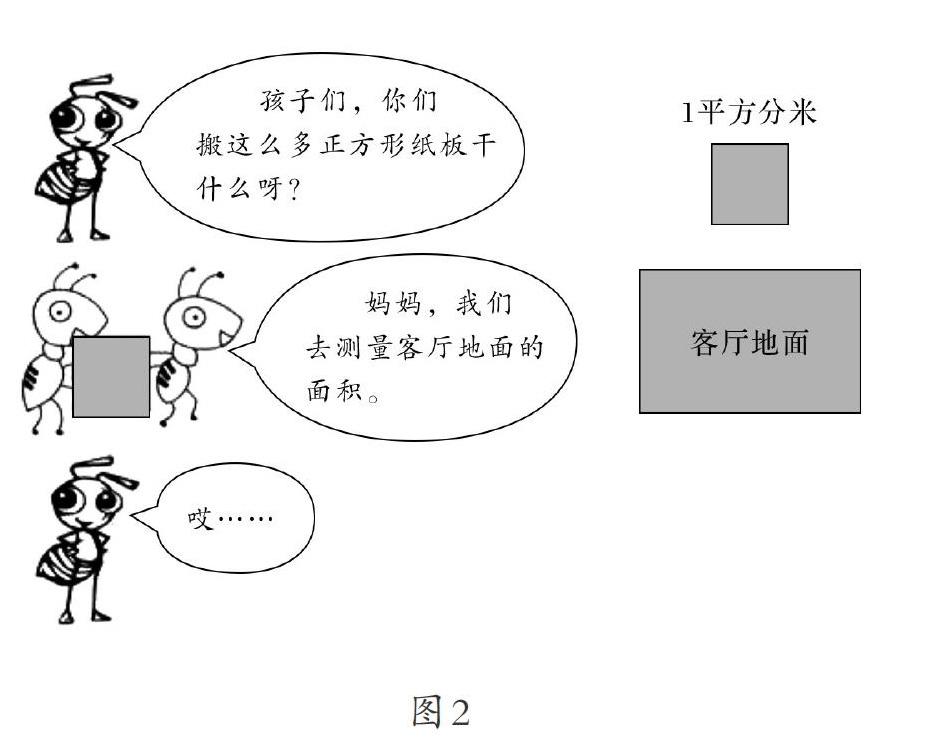
上課伊始，教師出示螞蟻媽媽和小螞蟻的對話情境（如圖2）。

教師首先請學(xué)生讀螞蟻媽媽和小螞蟻的對話，然后讓學(xué)生找出其中的數(shù)學(xué)信息。

師：從螞蟻媽媽和小螞蟻的對話中，你發(fā)現(xiàn)了哪些數(shù)學(xué)信息？

生：客廳地面是長方形，要測量長方形的面積。

生：用1平方分米的正方形測量客廳地面的面積。

……

由此，學(xué)生從螞蟻媽媽和小螞蟻關(guān)于“測量客廳地面的面積”的對話中引出測量工具——1平方分米的正方形;測量的對象——客廳地面，即長方形的面積;知道測量面積要用面積單位。這個故事情境為本節(jié)課的學(xué)習(xí)設(shè)置了懸念，為后續(xù)幫助學(xué)生理解將測量面積轉(zhuǎn)化成測量長度的可行性埋下伏筆，同時激發(fā)學(xué)生的探究欲望。

（二）直接測量求面積

教師先讓學(xué)生合作用1平方分米的正方形測量客廳地面的面積是多少平方分米（每組同桌都有6個1平方分米的正方形和1個代表客廳地面面積是6平方分米的長方形），然后全班交流反饋。請4組不同鋪法的同桌同學(xué)上臺和全班同學(xué)分享是怎樣鋪和怎樣數(shù)的。

第1組用的是將6個1平方分米的正方形鋪滿長方形且1個1個地數(shù)的方法，得出“一共鋪了6個1平方分米的正方形，面積是6平方分米”的結(jié)論;第2、3、4組分別用5個、4個、3個1平方分米的正方形鋪在長方形上，用1行鋪幾個、鋪幾行的方法數(shù)出，即“長鋪了3個1平方分米，寬鋪了2行，列式是3×2，面積是6平方分米”。根據(jù)學(xué)生的回答，教師相機(jī)板書“6平方分米=3個1平方分米×2行”。

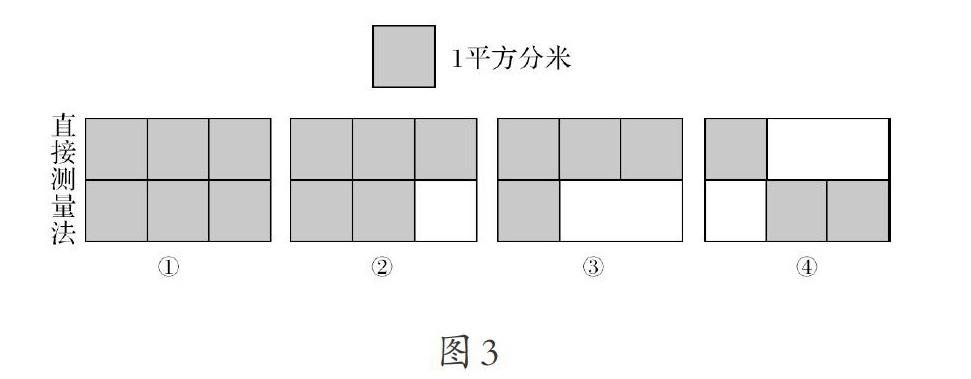
教師把上面鋪的4種圖形展示在屏幕上（如圖3），引導(dǎo)學(xué)生觀察、體會“這4組同桌同學(xué)鋪的方法——從鋪滿到?jīng)]鋪滿，用的正方形的個數(shù)越來越少，都測量出了客廳地面的面積”，接著指出：“像這樣用面積單位測量長方形面積的方法叫作直接測量法。”

通過用面積單位1平方分米的正方形直接測量客廳地面的面積，從鋪滿到?jīng)]鋪滿，既使學(xué)生體會到測量工具的不斷減少及方法變得越來越簡單，又使學(xué)生初步感知了面積單位的總個數(shù)與每行面積單位的個數(shù)、行數(shù)之間的關(guān)系。

（三）探尋本質(zhì)建模型

（1）說出下列各圖形的面積。

教師讓學(xué)生通過觀察說出圖4中兩個圖形的面積，進(jìn)一步感知不管是鋪滿還是沒鋪滿，都能看出1行有幾個面積單位，共有幾行，進(jìn)而列出乘法算式，求出相應(yīng)圖形的面積。情況①是鋪滿的情形：1行有4個1平方厘米，有3行，面積是12平方厘米。教師相機(jī)板書“12平方厘米=4個1平方厘米×3行”。情況②是沒鋪滿的情形：1行有5個1平方米，有4行，面積是20平方米。教師相機(jī)板書“20平方米=5個1平方米×4行”。

教師引導(dǎo)學(xué)生觀察黑板上的3個等式“12平方厘米=4個1平方厘米×3行”“6平方分米=3個1平方分米×2行”“20平方米=5個1平方米×4行”，歸納得出：等號左邊的數(shù)量表示的是面積單位的總個數(shù)，等號右邊的第1個數(shù)量表示的是每行面積單位的個數(shù)，等號右邊的第2個數(shù)量表示的是行數(shù)。所以根據(jù)這3個等式可以概括出“面積單位的總個數(shù)=每行面積單位的個數(shù)×行數(shù)”。

至此，我們從包含3個不同面積單位的3個具體的等式，利用不完全歸納法，構(gòu)建出計算面積單位總個數(shù)的數(shù)學(xué)模型：“面積單位的總個數(shù)=每行面積單位的個數(shù)×行數(shù)”，揭示了面積的本質(zhì)是包含面積單位的總個數(shù)，讓學(xué)生經(jīng)歷從特殊到一般的思維過程。

（四）間接測量顯方便

師：剛才同學(xué)們用面積單位直接測量長方形的面積。如果用直接測量法測量籃球場的面積，要用什么測量工具？

生：用1平方米的正方形來測量。

師：想一想，這樣測量會遇到什么問題？

生：要準(zhǔn)備許多1平方米的正方形，太麻煩。

生：1平方米的正方形很大，不方便攜帶。

生：測量的時候，兩個正方形之間要拼接得沒有縫隙，很難操作。

師：用面積單位直接測量長方形的面積這么麻煩，那有沒有更好的辦法呢？

教師在提出引發(fā)學(xué)生思維沖突問題的同時出示圖5，先讓學(xué)生量出長方形的長和寬，再要求學(xué)生用面積測量器來測量長方形的面積，最后引導(dǎo)學(xué)生思考長方形長、寬的長度分別與每行面積單位的個數(shù)、行數(shù)有什么關(guān)系：長方形的長是5厘米，每行就可以鋪5個1平方厘米;寬是3厘米就能鋪3行，面積是5×3=15（平方厘米）。

（2）量出下面長方形的長和寬。

教師小結(jié)：“剛才同學(xué)們不用鋪的方法，而是用量出長方形的長、寬的方法計算出了長方形的面積。測量長方形的面積，不用面積單位測量，而是用長度單位測量，這種測量方法叫作間接測量法。這樣測量長方形的面積既簡單又方便。”

（五）看“長”想“面”巧轉(zhuǎn)化

（3）先在下面方格圖上畫一個 長方形，然后填一填。

是不是所有長方形邊長的長度都分別和每行面積單位的個數(shù)、行數(shù)存在著這樣的關(guān)系呢？教師讓學(xué)生完成圖6的要求，完成后先同桌交流，后讓多個學(xué)生上臺分享自己的做法和想法。因為各個學(xué)生畫的長方形不同，教師要充分讓學(xué)生進(jìn)行多樣化的表達(dá)，從看得見的長度數(shù)量想到看不見的面積數(shù)量，然后，引導(dǎo)學(xué)生歸納出“長方形的面積=長×寬”，并讓學(xué)生理解公式中的“長”表示什么，“寬”表示什么。

（4）先量一量，再計算它們的面積。

然后，教師讓學(xué)生獨自完成圖7的要求，指名學(xué)生匯報自己做的結(jié)果：左邊長方形的長是5厘米，寬是2厘米，面積是5×2=10（平方厘米）;右邊正方形的長是3厘米，寬是3厘米，面積是3×3=9（平方厘米）。教師引導(dǎo)學(xué)生觀察第2個長方形的長和寬有什么特點，學(xué)生會發(fā)現(xiàn)第2個長方形的長是3厘米，寬也是3厘米，它是個正方形，就可順勢推導(dǎo)出“正方形的面積=邊長×邊長”。

在此基礎(chǔ)上，教師回頭讓學(xué)生說出兩個算式中的“5”“2”“3”“3”分別表示什么意義，學(xué)生用面積測量器驗證，再說出長方形面積公式、正方形面積公式中的“長”“寬”“邊長”分別表示什么意義，使學(xué)生能真正理解長方形面積、正方形面積與長和寬、邊長之間的關(guān)系，做到看見長和寬、邊長的長度想到與之分別對應(yīng)的面積單位的個數(shù)和行數(shù)。

從求面積的數(shù)學(xué)模型：“面積單位的總個數(shù)=每行面積單位的個數(shù)×行數(shù)”，到長方形、正方形面積公式，學(xué)生的思維經(jīng)歷了從一般到特殊的過程。

然后，教師回到課始的故事，問學(xué)生：“學(xué)到這兒，你知道螞蟻媽媽想對小螞蟻說什么嗎？”因?qū)W生對直接用面積單位測量的麻煩和間接用長度單位測量的方便有了深刻體會，所以學(xué)生會說：“螞蟻媽媽想對小螞蟻說，不要用1平方分米的正方形去測量，只要量出客廳地面的長和寬的長度就可以了。”

總之，計算長方形的面積，本來應(yīng)該用面積單位去測量，但因這種測量方法太麻煩，所以教師引導(dǎo)學(xué)生轉(zhuǎn)換思路，用測量長度的方法來計算面積。改變測量方法，但面積的本質(zhì)并沒有變化，因為長、寬的長度分別與每行面積單位的個數(shù)、行數(shù)之間存在著對應(yīng)關(guān)系，即如長是幾個長度單位，就可以擺幾個相對應(yīng)的面積單位;寬是幾個長度單位，就可以擺幾行。數(shù)值不變，變的只是意義。從直接測量法到間接測量法，教學(xué)的關(guān)鍵就是要讓學(xué)生通過參與測量、畫圖、觀察、思考、表達(dá)，經(jīng)歷“鋪滿—沒鋪滿—不鋪”的方法不斷簡化的過程，學(xué)生體會到直接測量的麻煩與間接測量的方便，在明白將測量面積轉(zhuǎn)化成測量長度的道理的同時，感知其中的變與不變，理解長方形的面積與它的長和寬之間的關(guān)系，進(jìn)而掌握面積的本質(zhì)。

（作者單位：福建省武平縣教師進(jìn)修學(xué)校）