“陷阱”式教學法在經管類微積分教學中的應用

（南京財經大學應用數學學院，江蘇 南京210023）

1 引言

微積分作為經管類本科專業的一門的重要基礎課，不僅為后續專業課學習提供了必要的知識，而且為培養學生的邏輯思維能力、分析及解決實際問題的能力奠定必要的基礎[1]。因此，微積分學習的好壞將直接影響到后續各專業課的學習效果以及學生繼續深造的積極性。但如今受到教學大綱的整體學時以及教學工作者對微積分教學存在的片面認識等影響，使微積分的教學效果及改革步履維艱[2]。具體表現在：首先，在教學內容上，不僅與高中數學知識存在一定的脫鉤，而且一些教學工作者對教學理念和方法存在固步自封的情形，嚴重影響經管類高等教育改革的步伐和相應的人才培養的需要[3]；其次，由于微積分的邏輯性、抽象性強，學習起來相對枯燥無味，從而導致一些學生放棄學習；一些愛好數學的學生，由于初期學習對一些抽象概念、性質以及定理理解不夠深刻，加之學而不精、學而不用，導致學習效果不佳。這些客觀原因的存在，都反映出微積分教學方法和教學理念改革的迫切性。

為了提高經管類微積分的教學效果，更好地為后續專業課程服務，本文提出了一種基于“陷阱”式的教學法，探討經管類微積分課程的教學改革。實踐表明，該方法能夠有效地提高學生對微積分中的抽象概念、性質以及定理的理解程度，提高其學習積極性，增強其專業的應用能力。

2 “陷阱”教學法的具體應用實例

2.1 在抽象概念中的應用

微積分中的一些抽象概念由于課時以及大綱要求等限制，導致學生對這些抽象概念理解不準確，甚至糊里糊涂。為了加深學生對這些抽象概念的理解深度，特引入“陷阱”式教學法。

例如：無窮大量和無界變量的概念在微積分的學習中扮演著非常重要的作用，特別是在極限運算中的作用尤為明顯。由于無界變量是對整個定義域而言，而無窮大量則是對極限趨勢來說的。在實際教學中，教師一般是在不同教學時段來進行講解這兩個概念，從而導致大部分學生對兩者的概念容易產生混淆，甚至把兩者混為一談。本文通過引入“陷阱”式教學案例，將兩者有機的結合在一起進行講解，讓學生更加深刻的理解無窮大量和無界變量的概念。

例1：判斷函數f(x)=xsin x在整個實數域上是無窮大量還是無界變量。

解：首先通過如下的方式使學生掉進無窮大量的“陷阱”之中，即令 x=2nπ+π/2 時，則所以f(x)是無窮大量。而后給學生分析正確結果如下：該函數是偶函數，故只需關注 x∈[0，+∞)，當 x取 nπ 時，則，所以f(x)不是無窮大量，但既然有一個子列可以使xsinx→∞，故f(x)無界變量。

例 2：判斷數列 an=［1+(-1)n］n2是無界變量還是無窮大變量。

解：首先使學生生搬硬套概念公式，即n2是無窮大量，1+(-1)n是常數，使其掉進錯誤的 “陷阱”里，即數列 an=［1+(-1)n］n2是無窮大變量。 然后給學生分析正確結果如下：因為a1=0,a2=4，a3=0，a4=8，L，a2n-1=0，a2n=4n，L 顯然數列 ｛an｝是無界的，又因為，所以數列｛an｝不是無窮大。

通過以上兩個“陷阱”式教學案例，可以使學生更加深刻理解無窮大量和無界變量的概念，并能夠準確判斷它們之間的關系,即無窮大量一定是無界變量，反之無界變量不一定是無窮大量，從而有助于提高學生學習微積分概念的興趣，讓其感受到微積分中抽象概念的魅力所在。

2.2 在具體性質中的應用

微積分中一些抽象的性質，同樣由于客觀原因限制，在授課的過程中，其理論證明過程往往是省略的，從而導致一些學生只會機械地使用。特別是在不滿足性質條件的情況下，如果繼續生搬硬套該性質，最終將得到錯誤的結果。

冪指函數在同濟版《高等數學》[4]中給出其一般形式是 f(x)＝u(x)v(x)并 u(x)＞0 且，掌握其求極限的方法是微積分教學中的一個重要內容，教材上一般都是直接給出其公式如下：

設 lim u(x)=A＞0，lim v(x)=B，則有

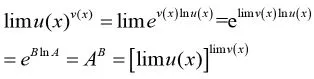
上述冪指函數的極限公式，使得本來一個復雜的函數極限問題轉化為分別求簡單的底函數u(x)和指函數v(x)的極限，然后對其極限進行冪運算的問題。但往往容易忽略冪指函數極限公式成立的先決條件為：函數u(x)和v(x)的極限存在且u(x)的極限大于零，想當然的生搬硬套冪指函數的求極限公式。

例3[5]：求

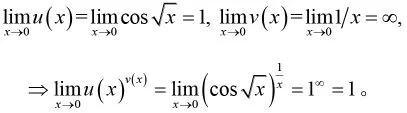
其次引入一個重要的極限反例，

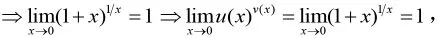
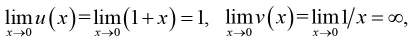
使學生意識到掉進了一個錯誤的陷阱之中。最后，給學生講解正確的冪指函數求極限公式，設

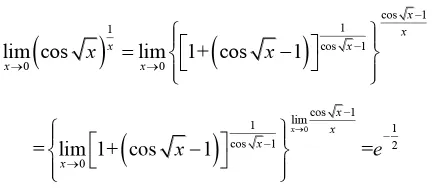
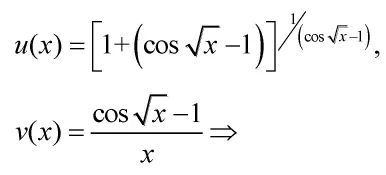
上述“陷阱”式教學案例可以使學生深刻的認識到冪指函數求極限法則的使用條件為：底函數u(x)和指函數v(x)的極限首先都要存在，而不是分別求底函數u(x)和指函數v(x)的極限，然后對其極限進行冪運算。

此外，學生在冪指函數求極限問題中，比較容易錯誤的第二種情況為：A=∞，B=0，=AB=∞0=1。我們同樣可以通過引入文[6]中的具體例子來設置“陷阱”式教學案例，幫助學生進一步理解和熟練運用冪指函數求極限法則。

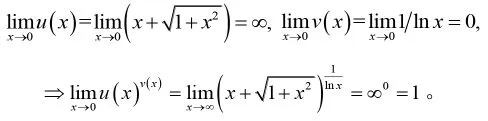
而后給學生分析正確的計算結果如下：

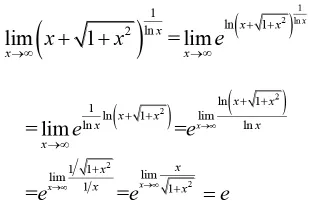
通過上述兩種情形的“陷阱”式教學案例，即“A=1，B=∞”和“A=∞，B=0”情形，能夠使學生在以后的學習中更加牢記并深刻的理解冪指函數求極限的法則。

2.3 在具體定理中的應用

考慮到教學大綱以及教學學時等客觀因素影響，教師在實際教學中對微積分中一些重要定理往往不給出詳細的理論證明，而僅僅講解如何有效地運用這些定理去解決問題。因此，往往會導致學生只會機械地使用這些定理，而對定理的實際含義一知半解，以至于在一些具體的運用中，缺少一些關鍵元素，導致定理的誤用。

例如：不定積分在微積分的教學中起到非常重要的作用，對后續定積分學習的好壞起到決定性的作用，而大多數同學對不定積分的定理一知半解。其中，容易出現的錯誤情況是把不定積分等同于求函數的原函數，從而在計算結果中缺少一個關鍵的元素常數C。我們可以通過引入如下“陷阱”式教學方案，使學生能夠深刻的理解不定積分的實際含義并能夠在實際應用中牢記在等式的后面加上常數C。

例6：求不定積分

通過這個“陷阱”式教學案例，可以首先讓學生掉進誤以為自己算錯的“陷阱”之中。然后我們通過如下方式給學生解釋上述兩個不定積分為什么都有兩種正確結果，從而使學生更加深刻理解到不定積分后面的常數C的重要意義。

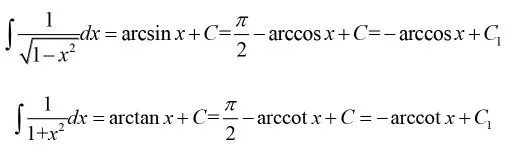
例7：求不定積分

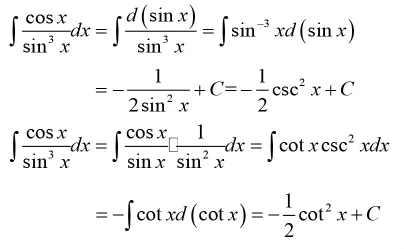
同樣通過這個“陷阱”式教學案例，首先可以讓學生掉進以為是自己算錯的“陷阱”之中；然后利用三角函數的恒等式關系給出正確的結果，讓學生明白兩種計算結果不一樣是由于忽略了不定積分后面的常數C的緣故；最后可以使學生更加深刻理解并認識到不定積分常數C的重要意義。

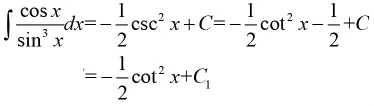
3 結束語

經管類微積分的教學改革是一項任重道遠的任務，在國家強力推行素質教育的今天，也應該隨著教學理念的革新以及教學手段的進步，不斷推陳出新。同時，教育主管部門也應更加重視基礎學科的建設，對微積分等數學課程給予更多傾斜[7]。本文探討了如何通過引入“陷阱”式教學案例，加深學生對微積分中抽象概念、性質以及定理的理解，以達到提高教學效果的目的。但在實際教學中，教師在引入“陷阱”式教學案例時，還應該根據實際知識的特點，有機地將“陷阱”式教學法引入到微積分教學中，不能東施效顰式的使用“陷阱”式教學法，其結果必然適得其反。