基于KNN算法的手寫數字識別研究

張 勇，馬亞州，侯益明

(山西農業大學 信息科學與工程學院，山西 太谷 030801)

0 引言

近年來，隨著科學技術的不斷發展和創新，人工智能迅速崛起，手寫數字識別在各行各業也有了應用，尤其在金融行業應用更加廣泛，但數字識別的錯誤在金融領域所帶來的后果是不可低估的[1]，因此，對手寫數字識別的準確率要求相當高。

為了提高手寫數字識別的準確率，本研究使用K最近鄰(K-Nearest Neighbor，KNN)算法構建分類器，識別手寫數字的準確率得到了很大的提高，而且實現方便簡單，運行速度快，值得進一步去研究。

1 KNN算法

KNN算法中存在一個樣本數據集合，在該集合中，每個數據對應一個標簽，即數據與其類別之間一一對應[2]，當輸入一個未知類別的數據之后，算法會計算該數據的每個特征與樣本數據集中所有數據對應特征之間的關系，具體計算方法：

(1)

將計算結果從小到大排序，選擇前K個距離最近的數據[3]，判斷其中出現次數最多的類別，將其作為輸入數據的類別。

2 數據準備

(1)收集0—9的手寫數字圖像共2 721張，包括1 856張圖像作為樣本數據集，865張圖像作為測試數據集合。在分類之前，需要將圖像進行預處理，可以使用圖形處理軟件，使之成為寬高是32×32 px的黑白圖像，并將圖像轉換為文本格式，使之成為32×32的二進制矩陣[4]。

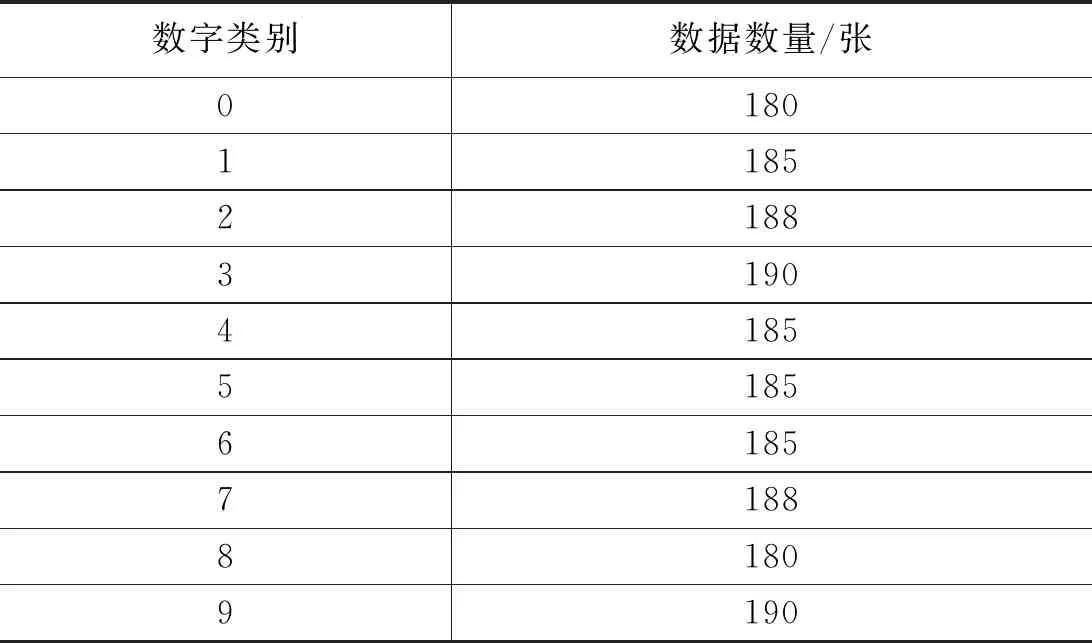
表1 樣本數量表

(2)要想使用KNN算法構造的分類器來識別手寫數字，就需要將數據處理之后得到的二進制矩陣轉換為1×1 024的向量，使之滿足數據集中一行代表一個數據的基本要求。

3 實驗過程

3.1 構造分類器

根據KNN算法的原理，構造一個有4個參數的分類器：待分類數據、樣本數據集、樣本標簽集、K值，依次進行新數據與樣本數據之間距離的計算、對距離由小到大排序、取得前K個距離最近的數據、確定前K個點中各類別出現的次數、出現次數最多的類別為新數據類別之后，即可預測出新數據的類別[5]。分類器流程如圖1所示。

3.2 參數K的選擇

K值的選取非常重要。(1)當K的取值過小時，如果有噪聲成分存在，將會對預測產生比較大的影響。例如，取K值為1時，一旦最近的一個點是噪聲，那么就會出現偏差。(2)如果K的值取的過大時，就相當于用較大鄰域中的訓練實例進行預測，學習的誤差會增大，與目標點距離較遠的實例也會對預測起作用，使預測可能發生錯誤。(3)如果K取N時，就是取全部的實例中出現次數最多的類別，則失去了預測的意義。

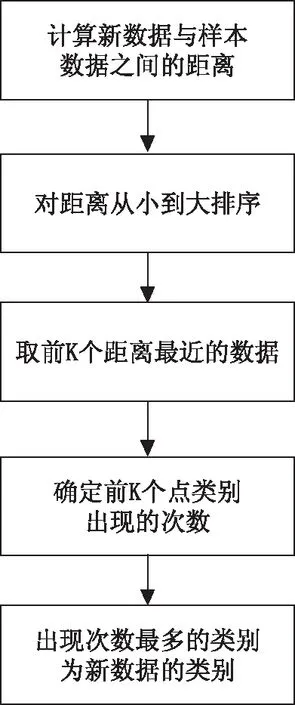
圖1 分類器流程圖

在選取K值時，應該盡量選取奇數，保證最終總會得到一個分類結果，如果為偶數，可能出現相等的情況，不利于分類。K通常是不大于20的整數，所以，從K取1開始進行測試，記錄分類結果的錯誤率，每次使得K值增加1，選擇錯誤率最低的K值作為分類器的K。分類錯誤率隨K值變化如圖2所示，據此進行分析，最終選擇K值為3。

圖2 分類錯誤率隨K值的變化

3.3 數字識別

用收集到的1 856張圖像作為初始的樣本數據集合，將每張圖進行預處理[6]，轉換為32×32的二進制矩陣，并存儲在文本文檔中，以X_i.txt格式命名，其中，X代表數據的真實分類，i代表該類別下的第幾個數據。將樣本數據集輸入到算法中，使用split()函數對文件名進行分割，取下標為0的元素，即為數據的真實類別。

使用構造好的分類器進行測試，對于數字0—9分別進行測試。測試前，要使用split()函數對文件名進行分割，以得到數據的真實類別。將測試結果與其真實類別進行比較，若不相等，則分類錯誤，錯誤次數加1，錯誤率如式(2)：

(2)

其中，x為錯誤分類的數據個數，N為進行測試的數據個數，可以得到手寫數字識別的錯誤率，以評價分類的效果。

4 結果分析

將每個類別的數據分別輸入到分類器中，各類別的分類準確率如表2所示。實驗表明，基于KNN算法構建的分類器用于識別手寫數字準確率最高可達98.89%，進一步證明了該方法用于識別手寫數字的可行性，具有實現簡單、運行速度快的優點，解決了人工處理大量數字的問題，具有很好的研究價值。

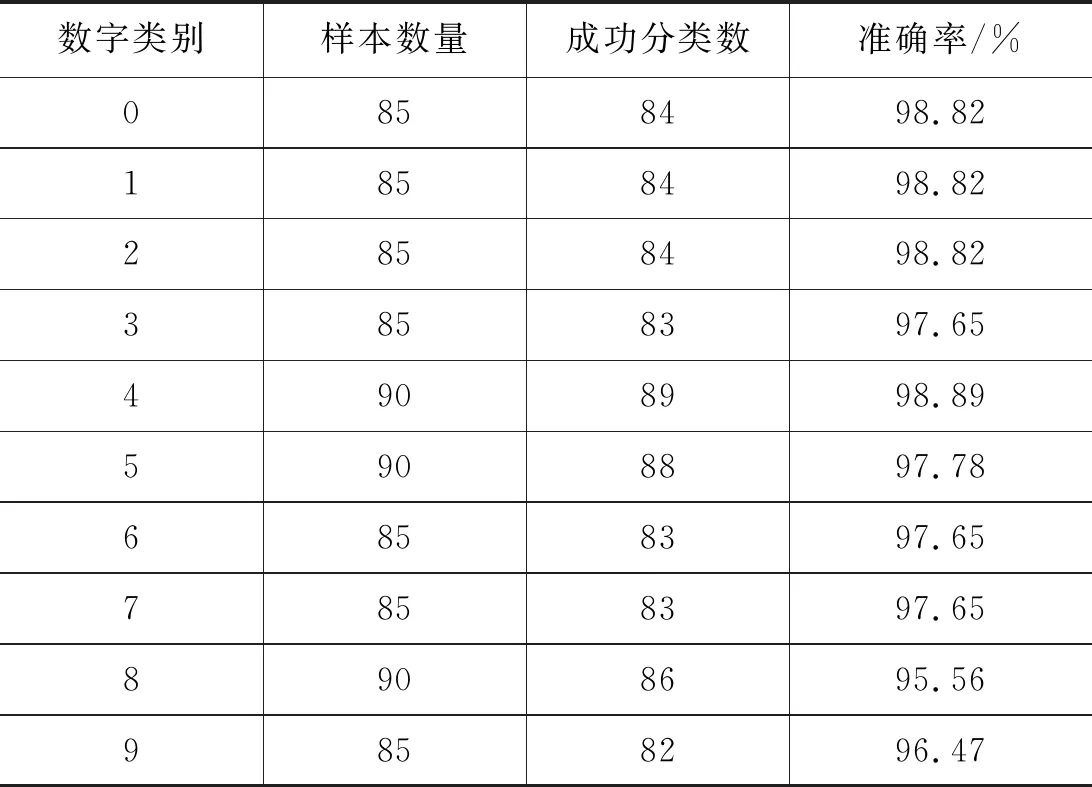
表2 各類別的分類識別準確率