2020年全國高考數學優秀試題解法賞析
蔡玉書 整理
2020年全國高考數學試題總體比較平穩,下面精選幾個試題加以分析.
試題1(2020年全國卷Ⅱ理17)已知△ABC中,sin2A-sin2B-sin2C=sinBsinC.
(1)求A;
(2)若BC=3,求△ABC周長的最大值.
解(1)由正弦定理得a2-b2-c2=bc①,
又由余弦定理得b2+c2-a2=2bccosA②,
(2)方法1 若BC= 3,即a= 3,設周長l=a+b+c=3+b+c.
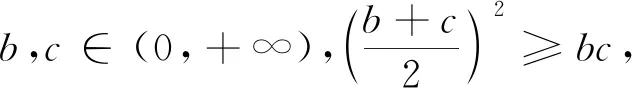



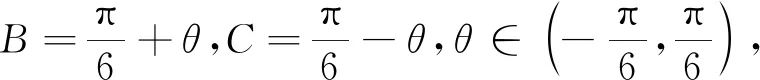

方法7 設b+c=t(t>3),則c=t-b,代入余弦定理b2+c2+bc=9,則關于b的一元二次方程b2-tb+t2-9=0有正根.
設f(b)=b2-tb+t2-9,由根的分布可得


(李家鑫重慶復旦中學 400012)

(1)求橢圓E的方程;
(2)證明:直線CD過定點.

(2)設C(x1,y1),D(x2,y2),點P坐標為(6,t)(t∈R),主要討論t≠0(t=0時,直線CD與x軸重合).





評注處理直線和圓錐曲線問題時,常用方法就是設而不求.通過相關交點法引入參數,得到含參方程,由方程對任意參數恒成立求出定點.

聯立方程整理得(x1+3)y2=3(x2-3)y1,即2λy1y2-(m+3)(y1+y2)+2(2m-3)y1=0.


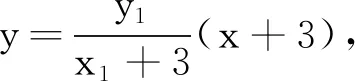
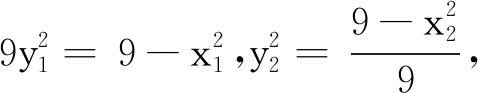
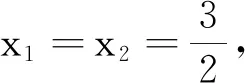
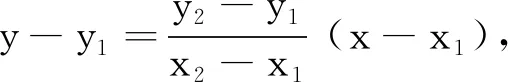

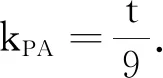
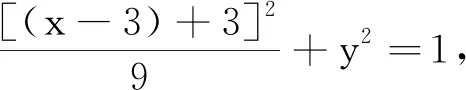

(劉小樹安徽省固鎮縣第一中學 233700)





(林琳福建省仙游金石中學 351200)

(1)求橢圓C的方程;
(2)點M,N在橢圓C上,且AM⊥AN,AD⊥MN,D為垂足.證明:存在定點Q,使得DQ為定值.

(2)設點M的坐標為(x1,y1),點N的坐標為(x2,y2).若直線MN不與x軸垂直,設直線MN的方程為y=kx+m.
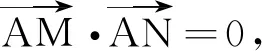
又點M,N在直線MN上,則有(x1-2)·(x2-2)+(kx1+m-1)(kx2+m-1)=0.
整理得(k2+1)x1x2+(km-k-2)(x1+x2)+(m-1)2+4=0. ①
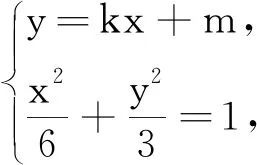
由于點A(2,1)不在直線MN上,故2k+m- 1 ≠ 0,故2k+3m+1=0且k≠1.


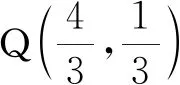
(董林山東省高青縣教學研究室 256300)
試題可以推廣到一般情況:
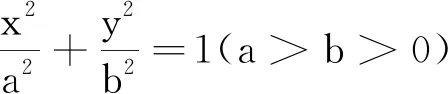
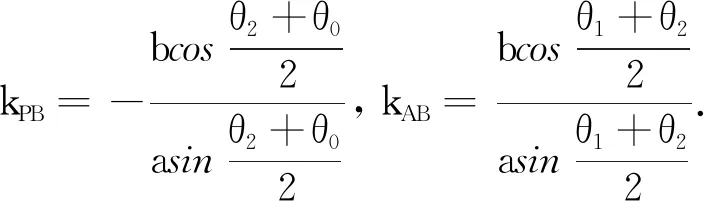




這是θ0,θ1,θ2之間應滿足的關系式.
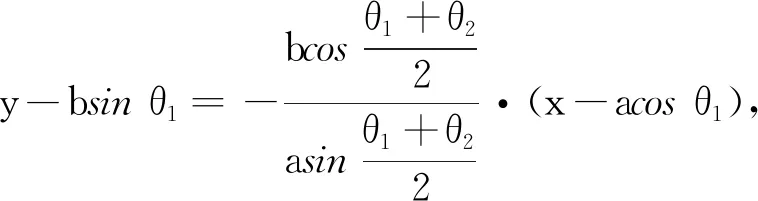
當PA或PB的斜率不存在時, 不難證明結論也成立.
(王晨江蘇省蘇州第一中學校 215006)

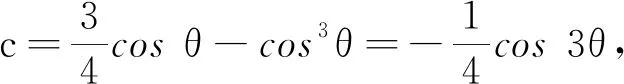
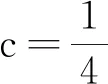

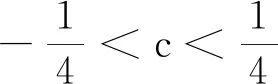
(王建偉中國科學技術大學 230026)

解法1當x=0時,a∈R.
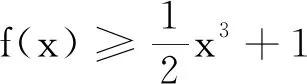

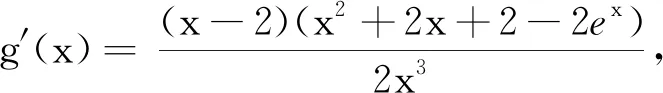


解法2當x=0時,a∈R;
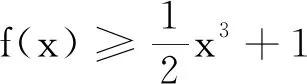
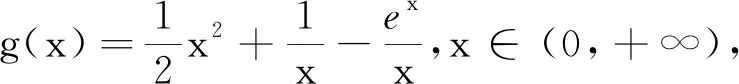
令h(x)=x2+x+1-ex(x>0),則h′(x)=2x+1-ex,h″(x)=2-ex.
令h″(x)=0,則x=ln 2,則當x∈(0,ln 2)時,h″(x)>0,h′(x)單調遞增;當x∈(ln 2, +∞)時,h″(x)<0,h′(x)單調遞減.
又h′(0)=0,h′(1)=3-e>0,h′(2)=5-e2<0,所以存在x1∈(1,2),使h′(x1)=0.
于是當x∈(0,x1)時,h′(x)>0,h(x)單調遞增;當x∈(x1,+∞)時,h′<0,h(x)單調遞減.
又h(0)=0,h(1)=3-e>0,h(2)=7-e2<0,所以存在x2∈(1,2),使h(x2)=0.
于是當x∈(0,1)時,g′(x)<0,函數g(x)單調遞減;當x∈(1,x2)時,g′(x)>0,函數g(x)單調遞增;當x∈(x2,+∞)時,g′(x)<0,函數g(x)單調遞減.
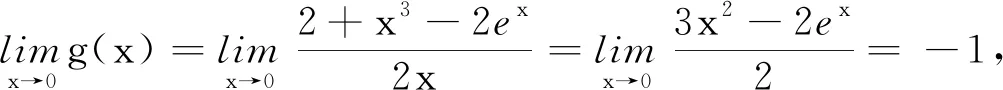


(洪汪寶安徽省安慶市第一中學 246004)

圖1
試題6(2020年全國新課程卷Ⅰ題20)如圖1,四棱錐P-ABCD的底面為正方形,PD⊥底面ABCD,設平面PAD與平面PBC的交線為l.
(1)略;(2)已知PD=AD=1,Q是l上的點,求PB與平面QCD所成角的正弦值的最大值.
解法1因為l?平面PBC,Q∈l,所以Q∈平面PBC.在平面PQC中,設PB∩QC=E,在平面PAD中,作過點P作PF⊥QD于F,連結EF.因為PD⊥平面ABCD,DC?平面ABCD,所以DC⊥PD.又DC⊥AD,AD∩PD=D,PD,AD?平面PAD,故DC⊥平面PAD.因為PF?平面PAD,所以DC⊥PF.又PF⊥QD,QD∩DC=D,QD,DC?平面QDC,故PF⊥平面QDC,從而∠FEP即為PB與平面QCD所成角.

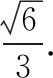

圖2
解法2如圖2,延長CB至G,使得BG=PQ, 連結GQ,GD,過點G作GM⊥平面QDC于M,連結QM,則∠GQM即為所求.
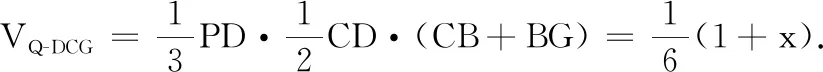
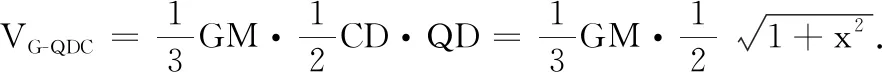
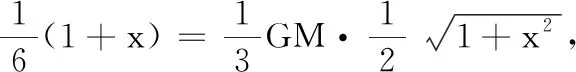

解法3如圖3,先將P-ABCD補形為正方體,再在正方體后面補一正方體.由圖可知P′C∥PB,過點P′作P′H⊥QD于H,易證P′H⊥平面QDC,故∠P′CH即為所求角.

圖3 圖4

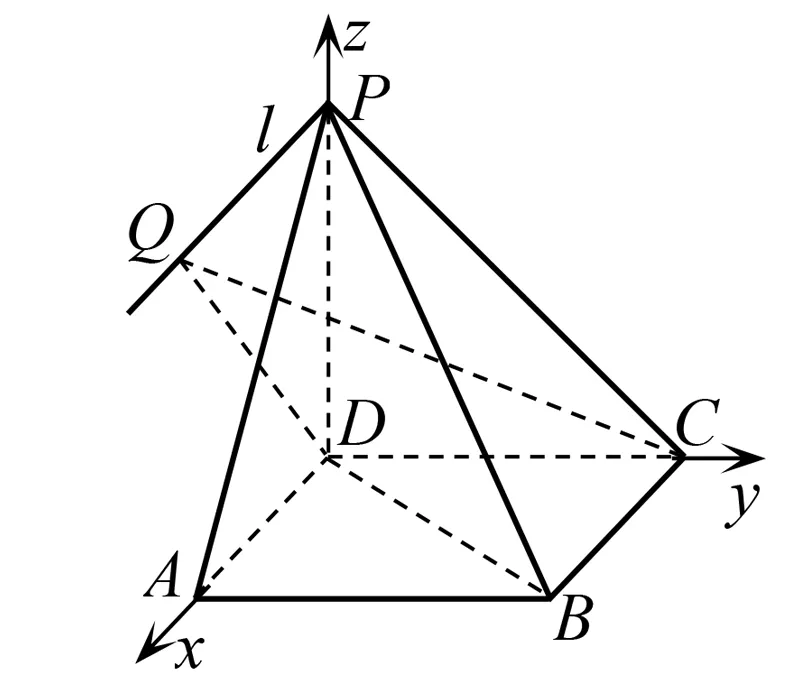
圖5

(張海泉江蘇省興化中學 225700)

