一道高三聯考題的解法探究及推廣

崔麗影 (江蘇省連云港市外國語學校 222006)

在高三高考數學備考過程中，教師應引導學生通過對基本題型的探究透析數學問題的本質，使學生完善自身的數學認知體系，形成解決某類問題的思路、步驟，即問題解決的程序，提升數學思維的靈活性和深刻性，進行有效的課堂教學，發展數學核心素養．本文以一道期中聯考題為例加以說明．

1 試題呈現

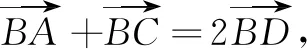
這是2020屆江蘇省連云港市十二所普通高中高三期中聯考試題的填空壓軸題，考查了解三角形中余弦定理、面積公式、三角函數關系，以及函數最值、平面向量、圓知識的交匯點等基礎知識的應用，又考查了直觀想象、邏輯推理、數學運算等數學素養，突出了能力立意，彰顯了數學思想方法．看起來背景熟悉、平淡無奇，實際上內涵豐富．該題解題思路較多，從不同的角度去審視它可以得出一系列優美解法，為學生提供了多樣化的選擇，是一道匠心獨運的好題．

2 思路及解法探究

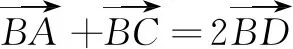
(3)思維障礙：題目條件中沒有給出△ABC的邊長和角度，只是隱含給出腰上中線的長度．不少學生想到中線長度公式或中線向量形式的表示兩邊平方，從而造成了思維上的定勢，將解題帶到了錯誤方向，導致無功而返．

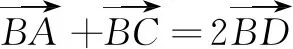
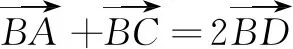
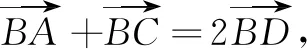
圖1

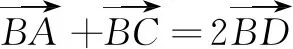
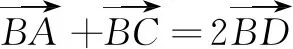
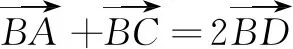
思路4 我們知道，一般在解三角形時都有這樣一個常識：遇到中點聯想中位線．故不妨取AB的中點E，連結DE，BD，CE,利用四邊形BCDE面積最大值進行求解．

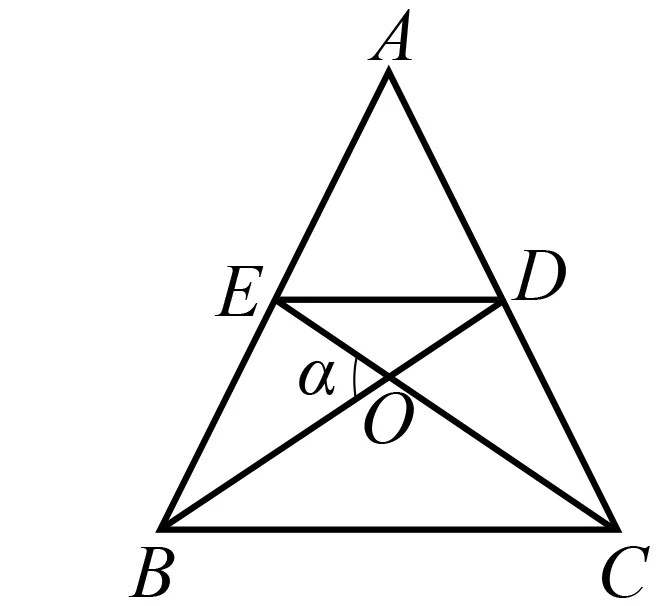
圖2

3 問題推廣

3.1 問題一般化

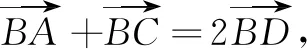
3.2 改變題設條件

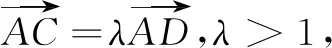
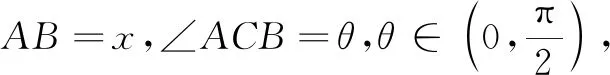
3.3 題設和結論都改變

變式1 在△ABC中，三個內角分別為A,B,C，AB=3，AC=6,角A的平分線AD的長為2，則∠A的大小為．

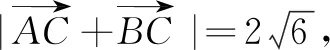
4 感悟與反思

在高三數學專題復習教學中，解題教學是主旋律．但教師很容易陷入“就題論題”的教學誤區中，僅僅停留在把題目的答案求解出來，以至于課堂變得枯燥無味，缺乏新知的生成，學生思維能力的靈活性和深刻性很難得以進一步提升．通過對該題解法和變式的探究，筆者對“如何在解題教學中發展學生的數學核心素養”有了進一步的思考．

首先，關注解題基本模型，聚焦問題表征．知識表征是一個狀態量，是靜態的．學生的知識表征可以是語言、文字、圖象、公式、概念圖、知識結構圖等．同一知識可以用多種方式來表征，教師要引導學生選擇最佳的方式獲取表征知識，幫助學生更好地探索解決問題的思路，猜想結果，發展學生的直觀想象素養．教師在此過程中引導學生思考解決思路的異同，通過類比歸納尋找解題模型，搭建問題線索，從問題表征的角度去比較問題解決思路的異同，形成解題程序．

其次，抓住通性通法，形成解題程序．通性通法是解決某類問題最合理的想法、最基本的思路、最普遍的操作程序．通過一題多解、多解歸一，讓學生掌握處理一個基本模型的方法，理解方法背后所隱含的數學思想方法，知道如何應用到其他情境中去，發展學生的數學建模素養和邏輯推理素養．變式訓練變化的是題目，不變的是通性通法，通過對問題變式的探究和原問題的推廣，幫助學生掌握一類數學問題的解法，從而形成解題模塊．