基于改進遺傳算法的多無人機協同任務規劃

趙民全

(解放軍92785部隊，遼寧 葫蘆島 125208)

0 引 言

多無人機協同任務規劃是針對2架及2架以上的無人機在復雜戰場環境中協同執行任務時，處理無人機之間的配合和以代價最小、算法最優、路徑最短為目標來進行任務規劃的技術。相較于單一無人機作戰，多無人機協同作戰有著更好的任務處理靈活性，并且通過相互配合，可以增加攻擊和防御能力，提高打擊效率和偵察成功率。

該技術的研究重點多集中于網絡化情況下聯合無人空戰系統協同作戰[1]。如自治編隊混合主動控制項目(MICA)[2]包括了無人機協同任務規劃、協同跟蹤、編隊控制等研究方向；異構無人機群實時協同與控制項目[3]是研究異構無人機協同控制及任務分配的技術，其理念就是將偵察區域劃分為多個分區,一架無人機完成一個分區的任務,分別建立單個的旅行商問題模型，再采用模擬退火算法進行進一步的優化；文獻[4]則是將無人機看作多個智能體，利用它們之間的交互對任務進行最優規劃。

采用多旅行商問題建立多無人機協同規劃模型，基于改進遺傳算法對多無人機任務進行規劃，采用模擬退火算法與基本遺傳算法相結合的方式對遺傳算法進行改進設計，并進行仿真驗證分析。

1 多旅行商問題建模

多旅行商問題(MTSP)[5-6]是旅行商問題(TSP)的進一步發展，是一種典型的組合優化問題，是解決在多名旅行商要拜訪多個地點時，如何能快速找到逐次抵達各地點一次后再回到起點的最短路徑問題。模型設計以點0作為起始點，表示旅行商的始發地，點1到點L分別表示不同的城市，m個旅行商從城市0出發分別去逐個拜訪,每一個城市都僅有一個旅行商到達,最后全部回到出發城市0。

建立多旅行商問題模型：

(1)

式(1)為目標函數式，為m個旅行商的總路程最小值，其中：

(2)

式(2)表示旅行商各自的路程，其中Cij表示旅行商經過對應弧段(i,j)用去的時間。

限定條件為：

(3)

式(3)表示從指定城市0出發，所有城市有且只有一個旅行商進行一次訪問。

2 基于遺傳算法的多無人機任務規劃

遺傳算法[7]是一種能有效求解最優化問題的算法，是遵循自然界“優勝劣汰”法則的方法。首先形成一組初始解群，然后通過選擇、交叉和變異等遺傳操作產生新一組滿足設定目標的候選解，循環開展適應度評價、選擇、交叉和變異遺傳等操作，逐步迭代優化，直至得到最優目標解。

在使用遺傳算法建模上，我們對適應度函數復制、交叉和變異等指標操作進行如下選擇和設定。

適應度函數一般要求非負,這里通過變換將多重旅行商問題的目標函數變為適應度函數。復制選擇上采用輪盤賭策略法，交叉在遺傳操作中起核心作用，可增強遺傳算法搜索能力。這里采用基本遺傳算法部分匹配交叉算子，其中變異在遺傳操作中是用來維持群體的多樣性的，對于多旅行商問題而言，染色體變異可以通過交換2個隨機位置上的基因來實現。

偵察無人機數量N為8時，假設需要偵察300 m×450 m的區域，進行仿真后可獲得基本遺傳算法規劃效果如圖1所示[8]。

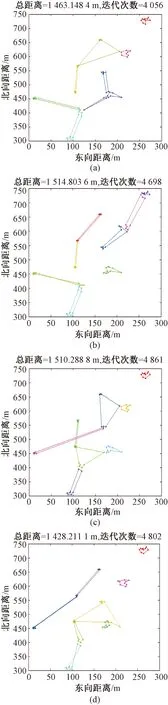
圖1 N=8時遺傳算法四次求解仿真曲線

實驗結果數據如表1所示。

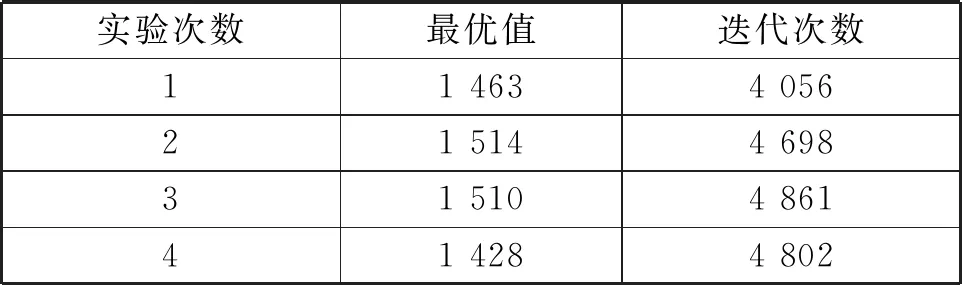
表1 N=8時遺傳算法仿真數據

可見當無人機數量為8架時，基本遺傳算法能夠基本完成對多無人機任務規劃問題的求解，給無人機分配目標位置使得每架無人機走過的路程開始不太均勻，幾次實驗中優化出的最短飛行距離和迭代次數的結果很接近，但求出最短距離和迭代次數數值都較高，優化效果有待提高。

3 基于改進遺傳算法的多無人機任務規劃

從遺傳算法實例仿真結果可以看出，其存在算法收斂性能差、找最優解時間長等不足之處。為使遺傳算法得到更好的應用，需要在改善算法搜索能力和提高算法收斂速度等方面加以改進。

現將模擬退火算法的Metorpolis準則[9-10]引入遺傳算法中,該算法是基于對溫度控制過程的模擬，用冷卻進度表來控制算法的進程，通過控制遺傳算法子代染色體的選擇來實現。隨著進化過程的進行,算法在控制參數T逐步趨向于零時最終獲取相對于全局的最優解。該方法使解的收斂從局部最優中跳出,最終達到全局收斂，同時實現了算法收斂速度的提升。

3.1 混合算法

模擬退火部分采用Metorpolis準則，采取內外雙層循環模式，內循環終止準則選用連續若干次搜索得到新解的變化較小；外循環終止準則選用最優解在算法運行過程中在較長迭代次數內保持不變，得到交叉退火之后的新種群：

(4)

(5)

式中：Pi為接受第i個新個體的概率；Pj為接受第j個新個體的概率；si,sj為第i,j個原始個體序號；ci,cj為第i,j個新個體序號；fit(*)為適應度函數；T為控制參數。

通過遺傳變異算子進行子代路徑變異操作獲得新個體，最后得到變異退火之后的新種群：

(6)

式中：i為變異前狀態；i′為變異后狀態。

根據溫度終止條件判斷是否需要重復以上步驟，通過逐步迭代獲得最優解。

3.2 實例仿真結果

無人機數量N為8時，假設需要偵察300 m×450 m的區域，混合模擬退火遺傳算法規劃效果如圖2所示。

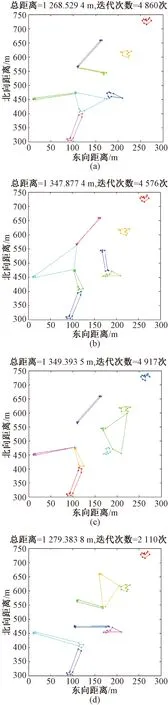
圖2 N=8時改進遺傳算法四次求解仿真結果

實驗結果數據如表2所示。

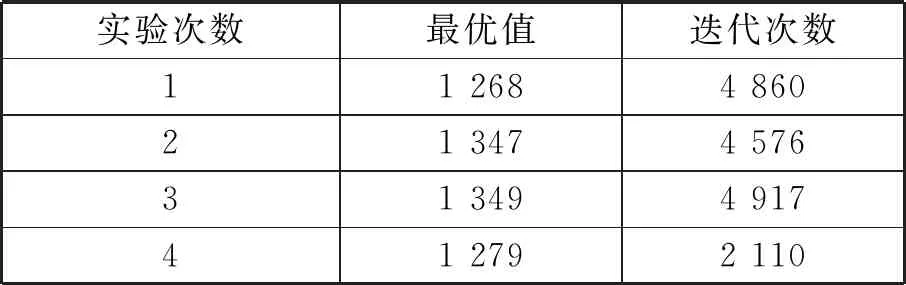
表2 N=8時改進遺傳算法仿真數據

可見當無人機數量為8架時，改進遺傳算法能夠完成對多無人機任務規劃問題的求解，優化出的最短飛行距離和迭代次數的結果很接近，求出的最短距離較小，以總飛行路程值來看，優化效果比較良好。對比2次仿真結果可知：在約束條件不變的情況下，混合模擬退火遺傳算法求得的最優值即最短飛行距離比基本遺傳算法都有明顯的優化，迭代次數上更少，即優化時間更短。由此得出，混合模擬退火遺傳算法確實使基本遺傳算法在尋得最優解的能力上得到優化。

4 結束語

本文以飛行時間最短作為優化目標，建立了組合優化模型，采用遺傳算法進行求解，并用多旅行商問題對模型進行修正，進而采用混合模擬算法和遺傳算法相結合的策略對傳統遺傳算法進行改進，將模擬退火算法與遺傳算法過程整合成一個雙循環，由模擬退火算法判定是否保留該解。最后，改進后的遺傳算法仿真實驗表明：基于模擬退火算法對遺傳算法的改進是可行的，具有一定的工程應用價值。