機載雷達數據融合效能評估

陳福年

(中國電子科技集團公司第三十八研究所,安徽 合肥 230088)

0 引 言

隨著現代機載雷達的發展，機載雷達裝備越來越豐富，功能也更全面。但是受到飛機運動平臺的限制，機載雷達的定位精度較差，在現有的雷達裝備下，僅僅依靠單個機載雷達無法實現對目標的高精度探測。為了提高機載雷達的探測精度，充分利用機載雷達的運動平臺優勢，本文介紹了運動平臺下的數據融合方法，并對融合精度提出了評估方法。

機載雷達由于其運動靈活的優勢，被廣泛用于各種戰場，能夠快速偵察戰場中的各個角落。但是由于機載雷達受限于載機平臺，一方面是由于雷達功率和雷達孔徑尺寸都受限，另一方面是由于目前國內慣性導航技術瓶頸，使得機載雷達的探測精度受限。文中采用雙機協同探測進行數據融合，可以極大地提高目標定位精度。典型場景為2部機載雷達通過戰場數據鏈互相通信，完成探測情報的數據共享，每一部雷達各自進行探測數據融合，通過雙機數據的融合提高定位精度，最后對雙機融合結果進行了仿真評估。文獻[1]對分布式協同定位的精度進行分析，但沒分析載機在運動過程中由于位置變化對協同定位精度的影響；文獻[2]對定位精度的計算過程分析得詳細入微，但是缺少雷達站不同方位分布情況下定位精度的差異；文獻[3]對組網數據融合過程中的誤差源進行細致的分析，但沒有給出有效提高組網融合精度的方法。

本文針對雙機探測時的位置不同，主要對融合后定位精度的影響進行了分析，通過定位精度的變化可以評估雙機協同帶來的精度提升。從目前文獻對數據融合精度的研究現狀來看，大多研究更關注融合過程中的數值計算方法和計算過程中的誤差，而對運動平臺的多雷達融合精度影響的研究較少。因此，文中針對機載雷達協同探測時，載機位置運動對探測的融合精度進行了分析和推導，并進行仿真驗證，對運動平臺的融合定位精度進行評價。文中分析了理想情況下，雙機協同探測時數據融合后雷達探測距離、方位精度的計算方法。

1 系統模型

雷達量測的系統誤差模型如圖1所示，量測距離為r，量測方位角為θ。雷達量測誤差服從高斯分布，量測距離標準差為σr，量測方位標準差為σθ。量測距離服從高斯分布(0，σr)，量測方位服從高斯分布(0，σθ)。雷達的量測誤差通常情況下存在距離誤差小而方位誤差偏大的特點，量測誤差示意圖如圖1所示。

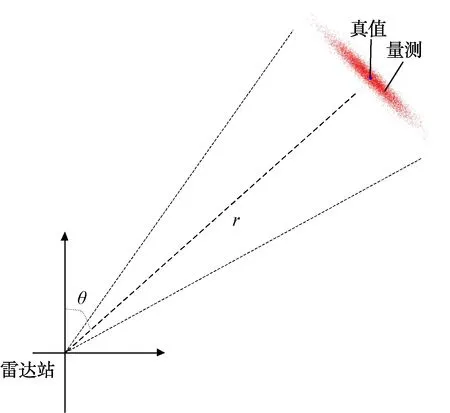
圖1 雷達量測誤差仿真模型

仿真場景如圖2所示，機載雷達B和C同時對目標A進行探測，雷達B和C將探測后的結果通過數據鏈共享探測數據，然后各自進行數據融合。我們假設機載雷達為兩坐標雷達，只能測得距離和方位，不考慮高度影響。假設機載雷達B探測到目標A的距離和方位為(r1,θ1)，機載雷達C探測到目標A的距離和方位為(r2,θ2)。這里假設系統可以做到時間精準同步，假設機載雷達B的量測距離均方根誤差為σr1，方位均方根誤差為σθ1；機載雷達C的量測距離均方根誤差為σr2，方位均方根誤差為σθ2。

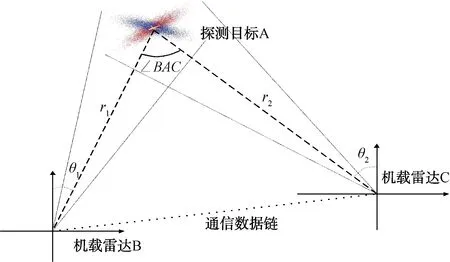
圖2 雙機協同探測場景

由于機載雷達B和C的運動，當雙機夾角∠BAC發生變化時，融合結果會發生變化，AB、AC的距離不同，融合結果也有區別，下面針對雙機的位置變化分析數據融合性能。

2 數據融合方法

數據融合處理是對多傳感器上報的量測點跡數據進行量測融合，融合完成后進行雷達目標跟蹤，本文只討論在卡爾曼濾波前進行量測融合后的精度變化情況。

量測融合方法可分為兩大類：量測合并(即數據壓縮)方法和串行處理方法。量測合并方法是指將多個傳感器在統一的時間軸上對同一目標的量測數據進行數據合并，將多個探測數據壓縮成1個數據。這種方法適合于天線同步掃描雷達，如一、二次雷達的綜合；而對于非同步采樣的多傳感器融合，如多部雷達數據的融合，則可以采用時間校準和目標狀態平移的方法，將異步數據變換成同步數據后再進行點跡的量測合并處理，最后進行跟蹤和濾波處理。

假設不考慮時間同步和狀態平移引起的誤差，設(r1,θ1)、(r2,θ2)分別為雷達1和雷達2的距離和方位的測量值，對2部雷達的量測值進行合并處理，可采用下式[4]對它們進行點跡合并：

(1)

(2)

上述公式為雷達融合誤差計算公式，從上述算式可以看出：估計的結果是各雷達的測量按精度加權；合并后點跡精度有所提高。

量測數據合并在數據融合處理中有著廣泛的應用，在通常的雷達融合處理中的處理流程是先接收多部雷達的量測數據，然后對接收的數據進行狀態平移和時間對齊，時間對齊以后就可以對量測數據進行數據融合，最后對融合后的量測進行常規的跟蹤濾波。本文只對數據融合結果進行分析，數據融合流程如圖3所示，不同顏色的圓點表示不同雷達的探測點。

圖3 數據融合流程

從圖3不難看出，本文的融合處理方法有一個顯著特點是先進行量測數據融合，然后進行跟蹤濾波處理。在實際情報融合處理系統中，遇到的情況比較復雜，這里不做討論，下面單獨就量測數據的融合精度進行分析。

3 融合精度計算

根據文獻[5]中提出的無偏轉換的方法，將雷達量測誤差無偏轉換到直角坐標系下，然后在直角坐標系下采用公式(1)、(2)計算融合后的量測位置，最后再轉換到雷達量測極坐標系下計算融合誤差，最終通過融合精度比較，評估融合效果。

步驟如下：

(1) 進行量測預處理，對量測進行轉換，計算直角坐標系下量測誤差的均方差。

(3)

(2) 展開公式，將2個雷達的量測代入式(3)得到直角坐標系下的量測誤差的均方差：

(4)

(5)

(3) 根據公式(1)、(2)計算融合后的直角坐標系下的量測值xF，yF：

(6)

4 仿真實驗及評估

假設2部機載雷達都能探測到目標，2部機載雷達與目標距離在50～350 km之間，兩機夾角在0°～180°之間變化，場景如圖2所示。單部雷達的測角精度0.25°，測距精度60 m。基于以上條件，主要分析兩機運動過程中的融合精度的變化。理想情況下，采用上節中數據合并方法對量測數據進行融合，通過蒙特卡洛仿真方法對融合處理后的定位精度進行評估。

距離融合精度隨夾角和探測距離的變化關系如圖4(a)所示。根據仿真結果可以看到，融合后，當雙機夾角較小的情況下，距離精度明顯提高，計算方法參考第3節中融合方法；當雙機夾角接近90°時，由于雷達方位誤差影響，距離精度下降，且目標距離越遠距離精度下降越大。融合后的方位精度大幅提高，仿真結果與理論相符。

方位融合精度根據夾角和探測距離的變化關系如圖4(b)所示，根據仿真結果可以看到融合后當雙機夾角較小的情況下，方位精度明顯提高，計算方法參考第3節中公式；當雙機夾角接近90°時，由于雷達距離誤差相比方位誤差較小，方位精度有更明顯的提升，通過較高的距離精度彌補雷達方位精度較差的影響。融合后的目標探測距離精度大幅提高，仿真結果與理論相符。

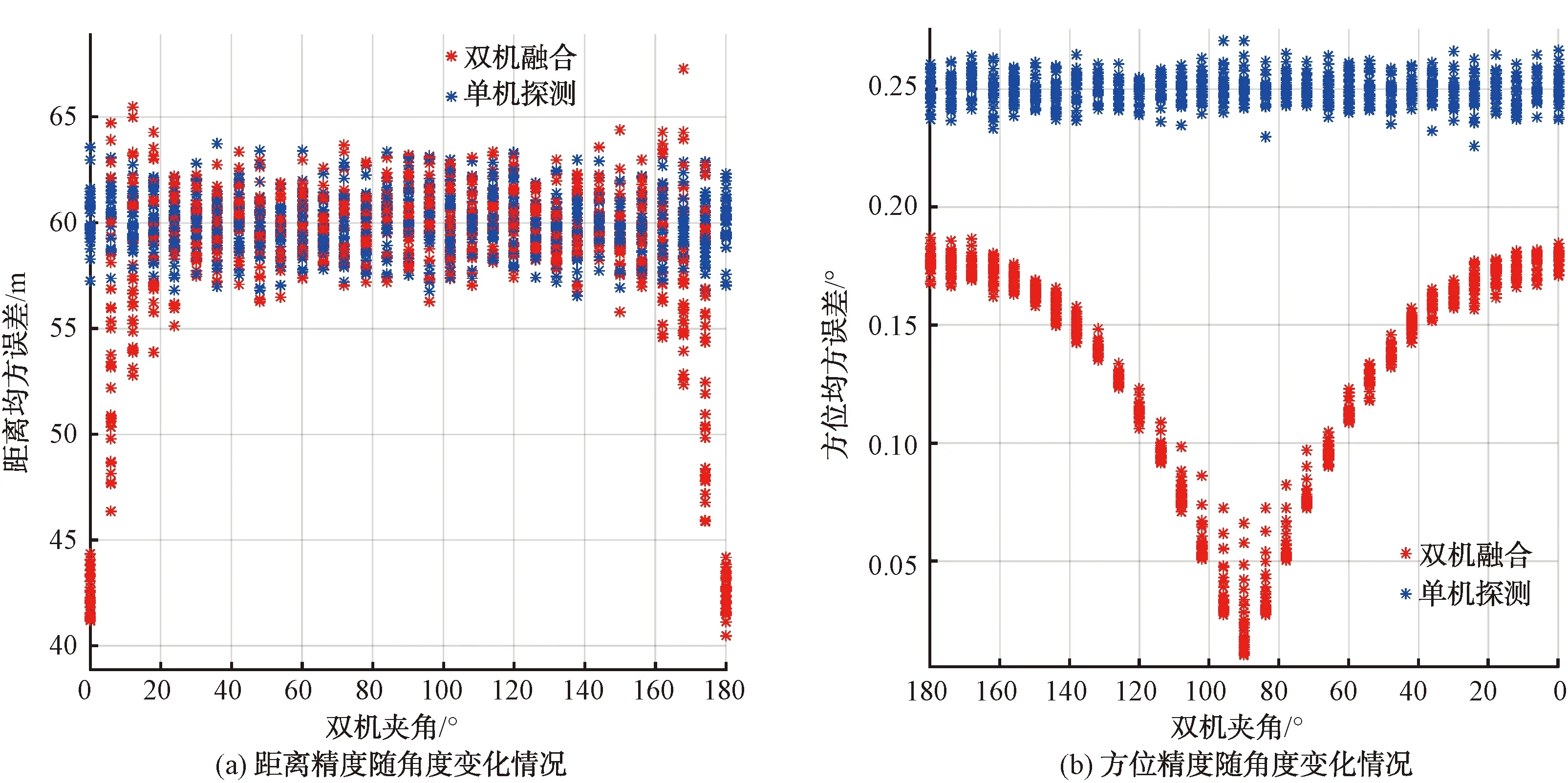
圖4 雙機協同距離方位精度分析

5 結束語

通過實驗表明，采用雙機協同或多機協同的方式進行數據融合，能夠有效提升雷達探測精度，可以彌補方位探測誤差較大的缺點。實驗中采用雷達測距誤差60 m，測角誤差0.25°的輸入精度，經過雙機融合后方位精度有明顯提升，距離精度可以采用過濾的方式保證距離精度不變，過濾處理后通過圖5可以看出雙機協同情況，雷達探測精度明顯提高，如表1所示。

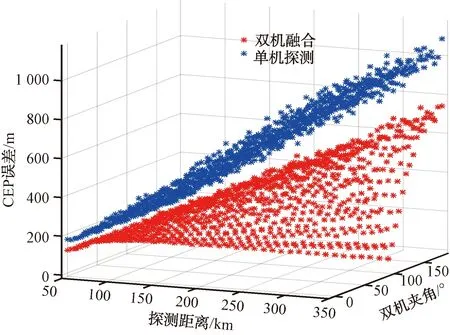
圖5 雙機協同CEP精度分析

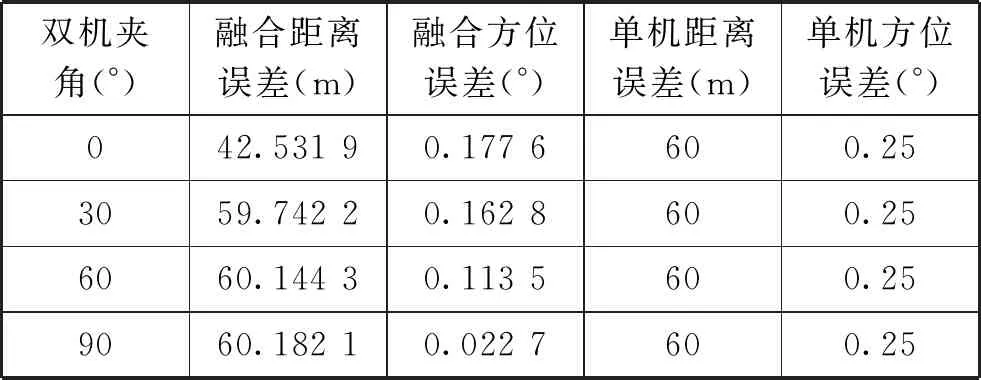
表1 雙機融合精度對比