一種基于傳輸零點插入的多通帶頻率選擇表面

唐旭英，萬國賓，付斌，韓先鋒，趙志穎

西北工業大學 電子信息學院，陜西 西安 710072

0 引 言

頻率選擇表面（FSS）是一種由相同單元沿一維或二維方向周期排列而成的周期結構。FSS 可以對特定頻率的電磁波進行選擇，控制其透射或反射。作為一種空間濾波器，FSS 被廣泛應用于艦船、飛行器等運動平臺的電磁兼容和電磁特性控制方面。隨著研究的不斷深入，FSS 的多頻化和多通帶技術逐漸成為研究熱點。分形單元、復合單元、互補單元等形式均可實現多頻帶選擇特性。其中，分形單元通過自相似分形迭代形成對應不同頻帶的諧振區域，實現多頻濾波；復合單元通過在周期內布置不同尺寸的導體結構，實現多頻濾波；互補單元通過幾何結構互補及相互靠近的導體層之間形成的強烈層間耦合效應，實現多頻濾波。

多頻FSS 的核心需求包括良好、穩定的濾波特性和通/阻帶的高可控性，但通阻帶越多，頻率響應越復雜，其穩定性和可控性往往也越差。為了解決這類問題，國內外學者提出了多種解決方案。在組合單元方面，Salehi 等[1-2]采用方形網柵和混合諧振結構，提出了具有角度和極化穩定性的雙通帶FSS，在傳輸零極點控制思想的基礎上，進一步提出了具有高階響應特性的FSS，并研究了此類高階FSS 的多頻化技術[3]；Sivasamy 等[4]對改進的雙方環結構進行優化，提出了一種用于屏蔽GSM 頻段的雙頻FSS，該結構不僅實現了雙頻帶阻，還具有優良的角度和極化穩定性。互補單元由于其剖面低且可形成高階濾波響應的優點，得到了廣泛應用；Wang 等[5]提出了基于方形互補結構的雙層緊湊FSS，可以實現三頻帶通濾波性能；Li 等[6]提出了結合曲折結構和互補單元的三通帶FSS，具備剖面低、小型化程度高的優點；Payne 等[7]將耶路撒冷十字和組合孔徑結構相級聯，利用兩者間的強烈耦合形成雙頻帶通的濾波特性，設計出了一種小型化、超低剖面和高選擇性的雙通帶FSS。同樣，有學者從分形單元和組合單元的角度開展了研究。Majidzadeh 等[8]提出了一種新型組合FSS，可以實現多波段和超寬帶濾波；Song 等[9]提出了一種工作在Ku，K 和Ka 波段的新型三通帶FSS；Palange 等[10]利用分形結構設計出了一種三頻帶阻FSS；Ferreira 等[11]提出了基于多個半圓特定組合的雙頻窄阻帶FSS，具備良好的角度和極化穩定性；Hussein 等[12]將2 種帶阻結構排布在同一周期內，設計出了一種應用于Ka 波段的雙頻帶通FSS，同時具備高透射率和高選擇性。同時，也有學者將以上幾種思想予以了結合。Wang 等[13]提出了基于曲折結構和組合單元的雙阻帶FSS，在TE 和TM 極化下具備0°～60°的入射角穩定性。

目前提出的方法大多僅針對單一需求，適用于特定場景。然而在實際工程應用中，多頻FSS往往需要在較大的入射角范圍內工作并兼顧2 種極化方式，各個通/阻帶需要滿足各自的性能要求，因而需要具備良好的可控性。針對以上問題，本文將基于傳輸零點插入和等效電路法（equivalent circuit method, ECM）設計雙/三通帶FSS 并展開分析。

1 基于傳輸零點插入的通/阻帶控制方法

從結構和功能的角度來看，FSS 主要分為2 類：一類是具備帶通特性的透射型結構（孔徑）；另一類是具備帶阻特性的反射型結構（貼片）。諧振時，這兩者分別形成傳輸通帶和阻帶。所謂傳輸零點插入，即通過合理配置位于同一單元內的透射和反射型結構的物理尺寸和空間關系，調整其諧振頻率和相互作用，將傳輸零點引入通帶范圍內，以使較寬的通帶分割為2 個或多個較窄的通帶。其中，透射型結構提供較寬的傳輸通帶，反射型結構則提供零點，共同形成多頻帶通的濾波響應。

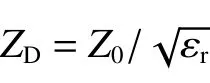
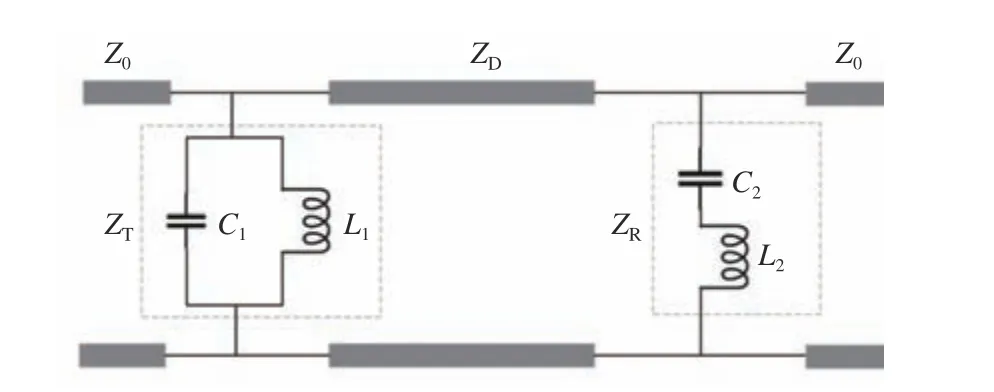
圖1 傳輸零點插入結構的等效電路模型Fig. 1 Equivalent circuit model of the transmission zero insertion structure

雙層級聯FSS 的輸入導納為

此時Zin=0，等效電路模型處于全反射狀態。

通過以上分析可以得到，如圖1 所示的等效電路模型具有2 個傳輸通帶和1 個位于2 個通帶之間的零點，具備雙頻帶通的濾波特性，零點兩側過渡帶窄。以上結論同樣可以推廣到多個反射型結構、其零點不互相靠近的情況。因此，基于傳輸零點插入的通/阻帶控制方法，可以得到雙頻或多頻帶通的濾波響應，并且可以通過控制透射結構和反射結構的諧振頻點，調整傳輸通帶和阻帶的頻率范圍。

2 多通帶FSS 設計

2.1 雙通帶和三通帶FSS

基于傳輸零點插入的雙通帶FSS 和三通帶FSS 分別如圖2～圖3 所示，為保證FSS 的角度穩定性，選用對稱性好且緊密排列的六邊形單元。雙通帶FSS 由3 個導體層和2 個薄介質層組成，2 層FSS1 具有完全相同的物理尺寸，由網柵和位于其內部的環形貼片組成，網柵內邊長為L1，貼片內、外邊長分別為L2和L3；FSS2 的內、外邊長分別為L4和L5的環形貼片。單元邊長為P，位于導體層之間填充的是 εr為2.2、損耗正切為0.001的介質，厚度為t。三通帶FSS 的FSS3 是在FSS1的環形貼片內部加載貼片結構而得到，為保證角度穩定性，選用了具備小型化特點的十字形環形貼片，其長邊為L6，短邊為L7，條帶寬度為w1。2 種FSS 的物理尺寸如表1 所示。

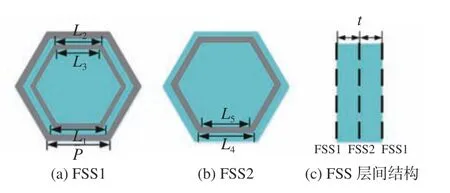
圖2 雙通帶FSS 結構示意圖Fig. 2 Dual-passband FSS structure diagram

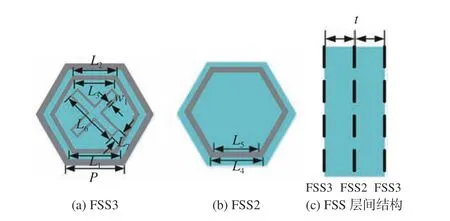
圖3 三通帶FSS 結構示意圖Fig. 3 Tri-passband FSS structure diagram

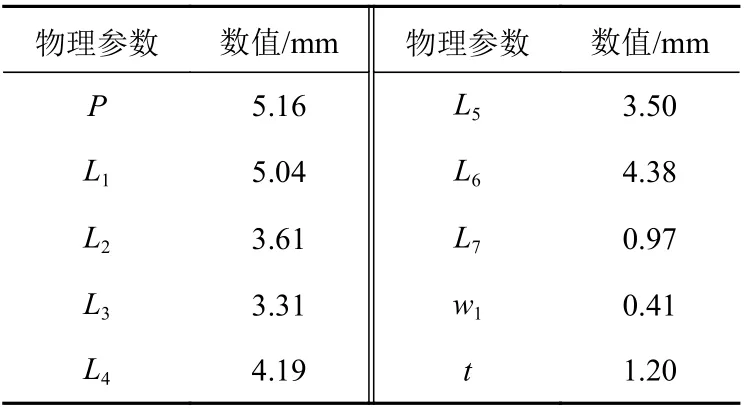
表1 雙通帶和三通帶FSS 物理尺寸表Table 1 Physical parameters of dual/tri-passband FSSs

垂直入射時，雙/三通帶FSS 和雙通帶FSS1級聯結構的傳輸曲線如圖4 所示。圖中，零點1～零點4 分別為4 個傳輸零點。

2 個FSS1 單元相級聯時，形成了范圍（-1 dB）為7.07～11.40 GHz 的寬通帶和2 個高頻零點，零點之間形成了阻帶，既為傳輸零點插入提供了足夠寬的通帶，又提高了高頻端的帶外截止性能。FSS2 的環形貼片諧振時產生了位于通帶內部的零點1，將寬通帶分割開來，其頻率為9.05 GHz。低頻處的通帶1 較為平緩，過渡帶較寬，高頻處的通帶2 處于零點之間，兩側形成了陡峭的截止區域，選擇性能良好。位于通帶2 高頻處的零點3是由FSS1 單元內部的環形貼片形成的。

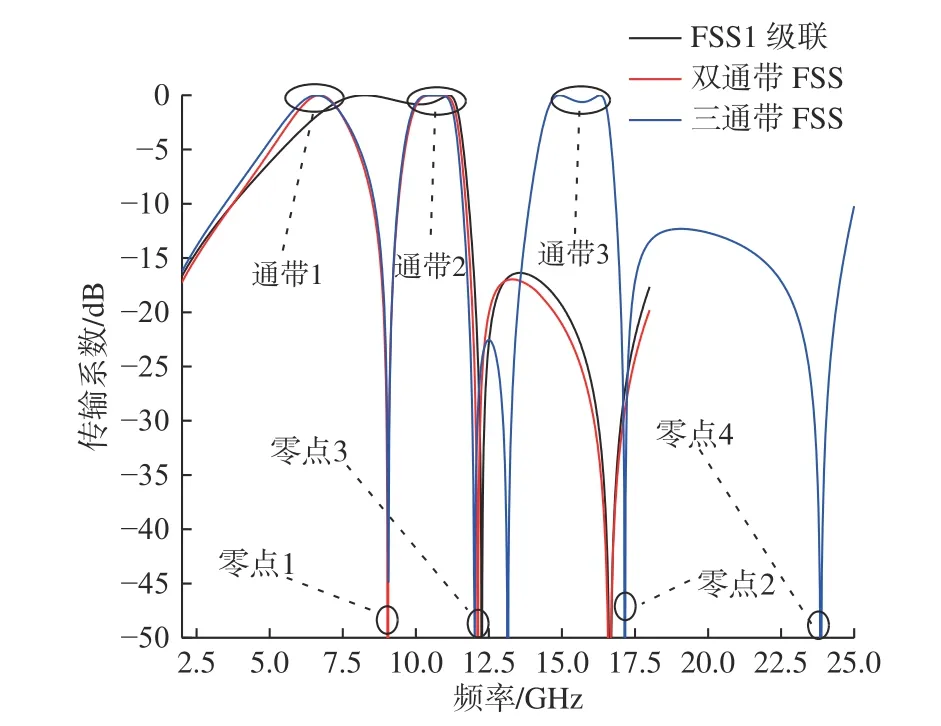
圖4 雙/三通帶FSS、雙通帶FSS1 級聯結構傳輸曲線Fig. 4 Transmission curves of dual/tri-passband FSSs and FSS1 cascade structure

加載十字形環形貼片后，在高頻處形成了通帶3，其范圍（-1 dB）為14.56～16.51 GHz，對十字形環形貼片單獨進行仿真可以得到其諧振頻率為零點2。通帶3 與通帶2 類似，位于零點之間，因此具備陡峭的邊帶，在高頻處同樣形成了寬闊的阻帶。零點4 位于零點2 的高頻端，由FSS3 內部的十字形環形貼片與FSS2 的環形貼片共同形成，且與零點2 共同形成了寬闊的阻帶，直到23.75 GHz，有效抑制了高頻柵瓣。三通帶FSS 不但保留了帶內平坦度高、選擇性能好的優點，且通帶3 沒有對低頻通帶的頻率和帶寬產生明顯影響，通帶間具備良好的獨立性，優化難度低，其性能參數如表2 所示。

表2 三通帶FSS 性能參數Table 2 Performance parameters of tri-passband FSS

2.2 等效電路模型分析

等效電路法是一種用集總電路形式對FSS 進行描述和等效的近似方法，可以較好地分析FSS的濾波特性，因良好的適用性而得到廣泛應用。雙/三通帶FSS 的等效電路模型如圖5 所示。

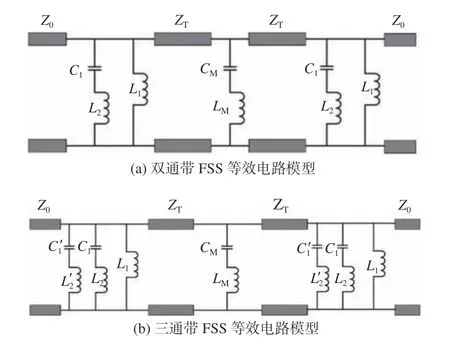
圖5 雙/三通帶FSS 等效電路模型Fig. 5 Equivalent circuit model of dual/tri-passband FSSs

由于選用六邊形單元，無法用經驗公式精準計算等效元件參數，故基于等效電路模型采用粒子群法進行優化擬合，得到電抗元件參數如表3所示。結合電路形式和電抗元件參數，使用軟件Matlab 計算得到的ECM 傳輸曲線和全波仿真結果對比如圖6 所示。由圖可以看到，雙通帶和三通帶FSS 的ECM 曲線和全波仿真結果吻合良好，通帶、阻帶范圍基本一致，差異主要在于零點的數量和頻率，且在高頻處更加明顯。當介質層較薄時，相鄰導體層間的互耦使各結構的工作頻率發生了偏移，圖5 所示的等效電路模型忽略了層間耦合，是ECM 曲線和全波仿真結果存在差異的主要原因。然而，本文中多頻帶通濾波由單元內各結構獨立工作形成，層間互耦僅為介質層較薄時出現的干擾，因此在進行濾波特性分析時完全可以忽略。ECM 曲線和全波仿真結果的一致性證明了等效電路法的有效性。

需要指出的是，雖然從理論上來說通過加載更多諧振于高頻端的反射結構來形成更多高頻通帶是可行的，但通帶數量存在上限。通帶1 形成的高頻柵瓣（也稱為寄生諧振）位于頻率較高處，斜入射時，隨著入射角的增大，柵瓣頻率逐漸降低，此時將嚴重影響反射結構所形成高頻通帶的傳輸效果。因此，當FSS 需要工作在斜入射條件下或需要在較寬的入射角范圍內工作時，本文所提供的方法能夠形成的通帶數量是有限的。

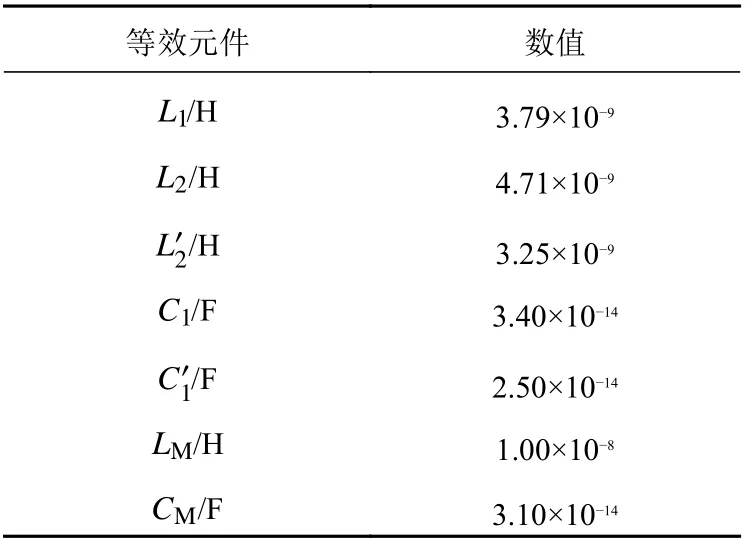
表3 雙/三通帶FSS 的ECM 等效元件參數Table 3 ECM parameters of dual/tri-passband FSSs

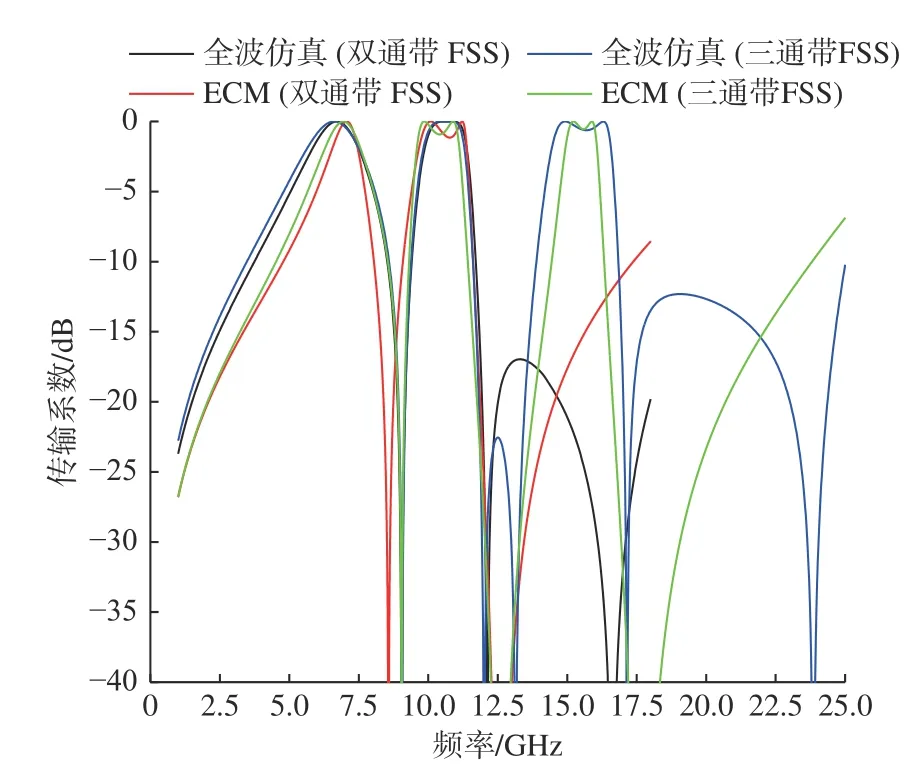
圖6 雙/三通帶FSS 的ECM 與全波仿真結果Fig. 6 Transmission curves of dual/tri-passband FSSs from fullwave and ECM simulation

3 仿真分析

垂直入射時，分別改變三通帶FSS 的L4和L6，傳輸曲線如圖7 所示；入射角為0°～45°時，三通帶FSS 的傳輸曲線如圖8 所示。

零點1 的頻率受FSS2 六邊形環尺寸控制，當L4減小時，零點1 向高頻端移動，通帶1 和通帶2 的中心頻率隨之增大，帶寬分別增大和減小。通帶3 的頻率范圍受FSS3 十字形環形貼片尺寸控制，當L6減小時，零點2 和通帶3 同時向高頻端移動，通帶3逐漸展寬。同時，通帶3 隨L6變化移動時，通帶內插損基本保持不變。

斜入射時，不同極化方式下的傳輸曲線共形性良好，共同通帶較寬。由于高頻通帶比低頻通帶更接近于高頻柵瓣，隨著入射角的增大，當柵瓣頻率向低頻端移動時，通帶3 的穩定性比通帶1 和通帶2 的差。當入射角為45°時，各通帶在不同極化下仍可以保持共同帶寬，這證明三通帶FSS 具有良好的角度和極化穩定性。

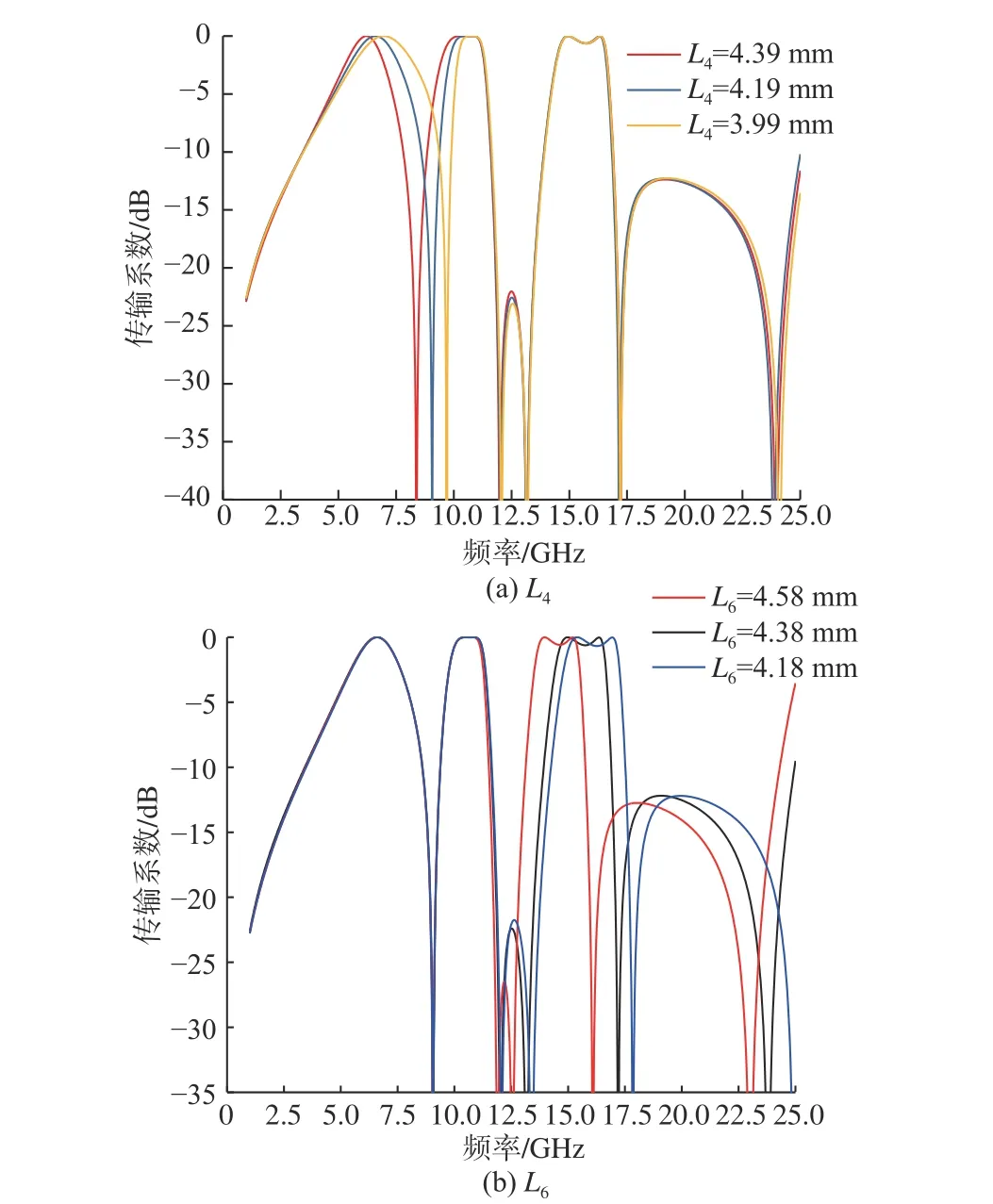
圖7 三通帶FSS 傳輸曲線隨L4 和L6 的變化情況Fig. 7 Variation of tri-passband FSSs transmission coefficients with respect to L4, L6

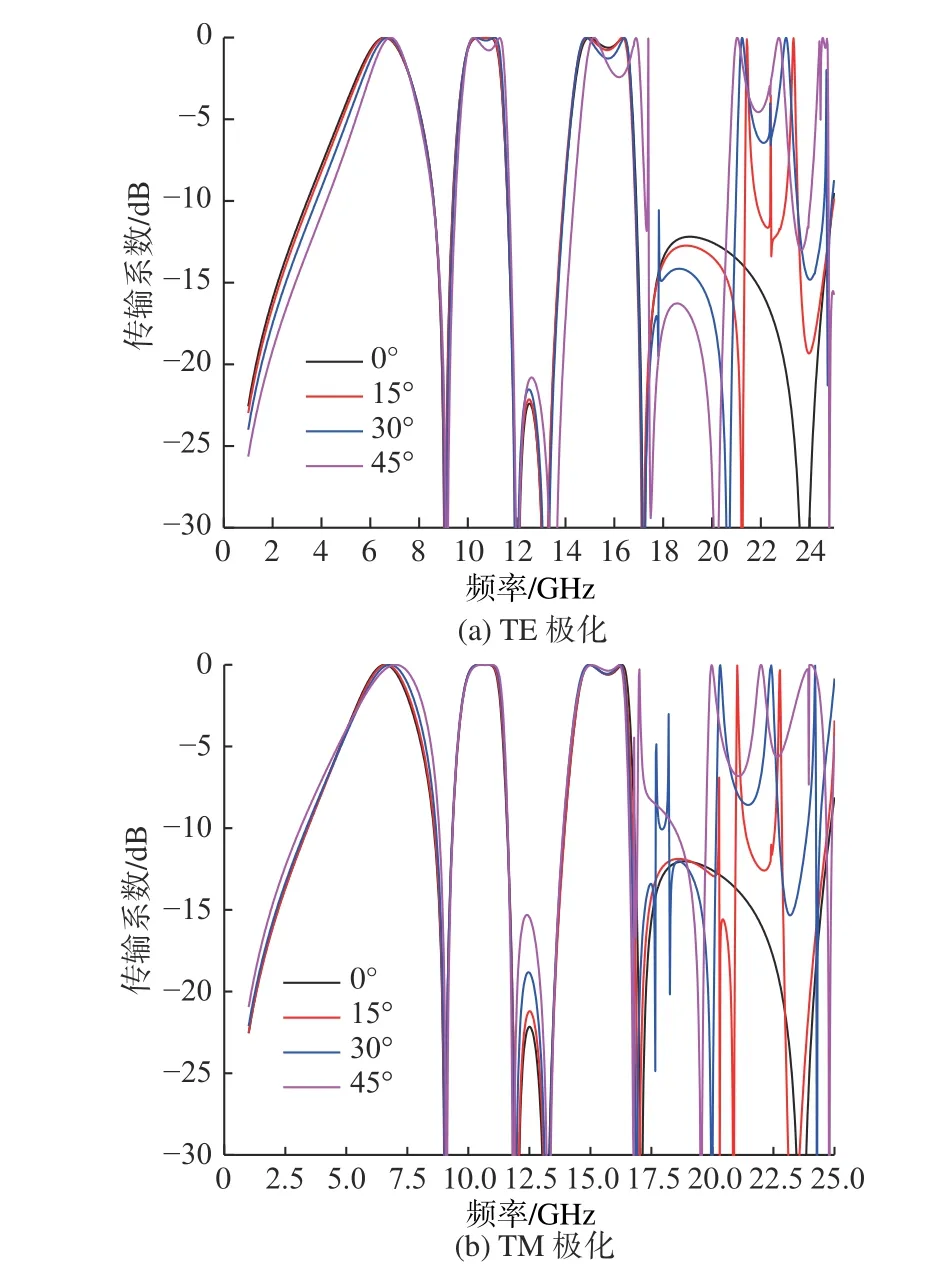
圖8 三通帶FSS 傳輸曲線隨入射角的變化情況Fig. 8 Variation of tri-passband FSSs transmission coefficients with respect to incident angle

4 結 語

本文基于傳輸零點插入方法，利用帶阻結構和帶通結構進行同層及不同層組合，實現了雙/三通帶的選頻效果，并基于等效電路法對這一方法的原理進行了分析，適用于0°～45°入射范圍和2 種極化方式。其中，三通帶FSS 具備位于C，X和Ku 波段的通帶和位于通帶之間的多個零點，零點在通帶兩側形成傳輸截止效果，有效縮短了過渡帶，提高了選擇性能。位于高頻處的零點形成了寬闊的阻帶，有效抑制了高頻柵瓣。仿真結果顯示，本文所提的FSS 具備0°～45°范圍內的角度和極化穩定性，且可以實現通/阻帶的獨立控制。