多設備長條形基座的螺栓受力確定方法

王凡超，王福花，吳劍國，李鈞暉，鄭杰瑜，陳沈

1 中國船舶及海洋工程研究院 上海 200011

2 浙江工業大學 土木學院，浙江 杭州 310023

0 引 言

某些大型艦用液壓設備結構復雜，液壓油缸行程較長，通常被集成安裝在長條形基座上，包括公共基座和船體基座，其中公共基座安裝的是多個功能各異的船用設備，通過螺栓群與船體基座連接。由于此類長條形基座尺寸較大，螺栓分布散亂，公共基座與設備相比剛度較小，且加載的載荷分散在多臺設備上，所以確定螺栓受力情況是基座設計和船體支撐強度校核都必須重視的問題。

在各類普通基座中，錨機基座長度相對較小，一般僅安裝一臺設備，螺栓分布較為集中，對螺栓的受力分析主要采用彈性分析法[1-4]。在分析普通基座的受力時，通常假設基座面板為剛性體，螺栓為彈性體，并分配螺栓受力。然而，對于長條形基座而言，因總體尺寸較大，若將其視為剛性體顯然不合適。不僅如此，長條形基座上還安裝了多組設備，局部載荷多，每個外載荷并未分配到所有螺栓而是部分螺栓上。

目前，對螺栓群受力的研究大多關注的是螺栓布置、接觸面摩擦等方面。例如：朱銘和王斌華等[5-6]通過建立考慮了接觸狀態的三維有限元實體模型，對4 種不同螺栓布置方式在拉力載荷作用下的板件相對位移、板件應力以及接觸面的摩擦應力分布狀態等進行了模擬；張文元和扈玥昕[7]提出一種以連接件單元代替螺栓的簡化模擬方法，并應用到了簡化的殼單元連接模型中；沈詣等[8]優化了一種大型結構的螺栓連接有限元模型簡化方法，計算了3 種不同載荷作用下模型的受力；李國強等[9]探討了螺栓連接的模擬方法，并對一處螺栓結構進行了計算與強度校核，結果表明該計算方法可行；佘凱等[10]采用不同邊界處理條件對結構進行有限元分析，得到了結構螺栓處的載荷數值模擬方法。

綜上所述，現有研究主要是分析普通基座螺栓的受力情況，而鮮有對安裝有多組設備的長條形基座螺栓受力情況的研究，且在實際工程應用中也多采用非常保守的估算方法處理，導致分析效率和得到的精度不高。

為保證設備正常使用和船體支撐結構安全，有效確定安裝了多組設備的長條形基座螺栓的受力情況，本文擬將多組設備的長條形基座視為幾條連續梁結構，運用連續梁理論，提出一套在多種局部載荷作用下的長條形基座螺栓群受力近似計算方法和有限元分析方法，并結合算例對計算過程和精度進行說明。

1 有限元方法

1.1 基座的有限元模型

圖1 所示為長條形基座的有限元模型，可通過有限元方法確定此類基座螺栓的受力。圖2 所示為公共基座、船體基座和周邊相互連接的結構。鑒于長條形基座的有限元模型較大，結構較復雜，為簡化計算，省略了對螺栓群影響較小的一些部位和細節。經驗算，若僅需確定螺栓的受力，模型范圍僅包括公共基座和船體基座即可，無需包含甲板結構，如圖2（a）所示；若需計算基座及其支撐結構的應力，模型范圍可包括一定范圍內的船體結構，如圖2（b）所示。對于船體基座上的面板、腹板和公共基座的下面板，腹板應采用板（plate）單元，公共基座的上面板可采用桿（rod）單元進行簡化，基座腹板高度方向應不小于2 個單元。

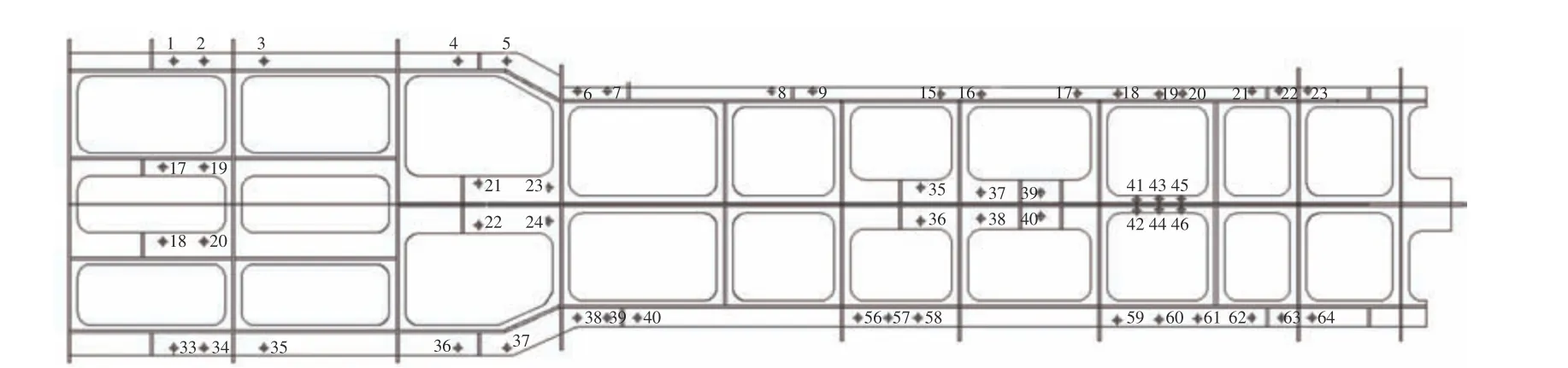
圖1 長條形基座結構圖Fig. 1 Schematic of the long-strip base structure

1.2 螺栓模擬

為準確計算螺栓的受力，在有限元模型中，忽略面板間的接觸與摩擦作用，避免模擬螺栓的單元承受彎矩。根據基座的結構形式，若長條形基座采用抗剪鍵，則用桿單元模擬螺栓；若不采用抗剪鍵，則用梁（beam）單元模擬螺栓，并將梁單元與船體基座上面板相連的節點改為鉸接形式，如圖3 所示。

圖2 有限元模型和邊界約束Fig. 2 Finite element model and boundary constraints

1.3 載荷施加與邊界處理

長條形基座受到多個局部載荷的作用，各載荷均采用多點約束（multi-point constraint，MPC）方式施加到每臺設備的機腳區域。若結構設置了抗剪鍵，則抗剪鍵所在位置的船體基座面板與公共基座下緣面板采用MPC 關聯，以限制其在水平方向的位移；若僅需確定螺栓的受力，則約束船體基座腹板下緣3 個方向的線位移，如圖2（a）所示；若需計算基座及其支撐結構的應力，則約束模型中船體結構邊緣3 個方向的線位移，如圖2（b）所示。

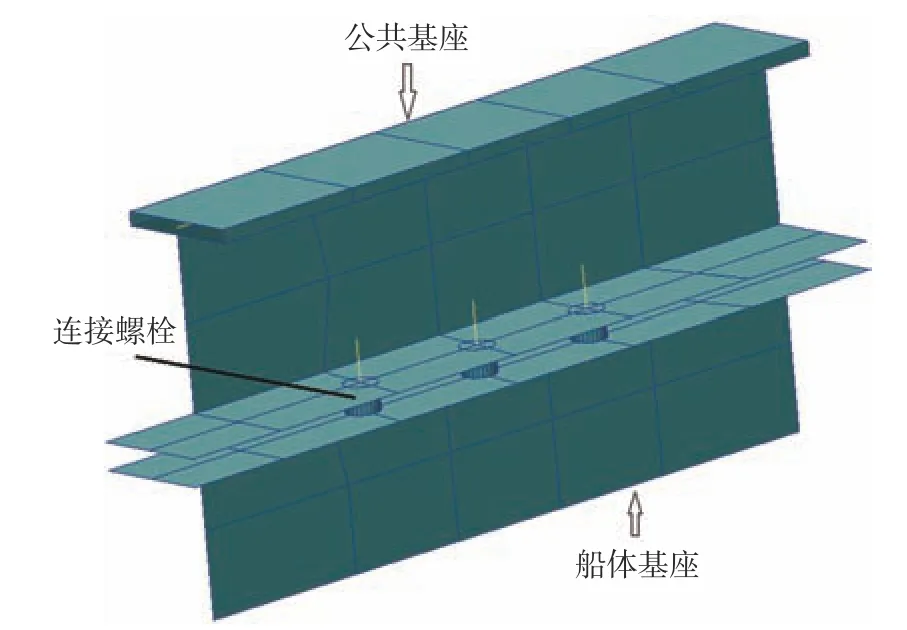
圖3 長條形基座局部詳圖Fig. 3 Detailed view of the long-strip base

1.4 螺栓力的計算

首先，將模型提交到有限元軟件進行計算，輸出螺栓單元的軸向應力，對于未設置抗剪鍵的支座，還需輸出螺栓單元的剪應力。然后，將螺栓單元的軸向應力及剪應力乘以螺栓橫截面面積得到各螺栓的拉力和剪力。

2 螺栓受力的近似計算方法

作用于設備上的水平力和垂向軸扭矩產生的剪力一般不由螺栓承載，而由基座的抗剪鍵承載，故本文僅研究螺栓所受拉力。基座受到的外載荷包括拉力、縱向彎矩、橫向彎矩及其組合力，其中縱向彎矩作用平面沿基座長條方向，橫向彎矩作用平面垂直于基座長條方向。

本文在多個長條形基座有限元分析的基礎上，根據此類基座的變形規律，首先給出若干假設，然后運用力和力矩的平衡原理，提出一套在多載荷作用下長條形基座螺栓群受力的近似計算方法。

主要假設如下：

1） 長條形公共基座被視為由若干個連續梁組成，螺栓被視為各梁的支座。

2） 基座上安裝的設備被視為剛性體，設備底座外輪廓為載荷直接作用區域（即有限元MPC 的作用范圍），假設底座外輪廓線與連續梁的交點為載荷作用點。

3） 外載荷分解為基座受到的拉力、縱向彎矩、橫向彎矩3 種形式的載荷，并按照各自假設的規律分配到每條梁上；按照連續梁理論，根據支座受力大小與支座至加載點的距離成反比，近似求解出每個螺栓上的拉力。

圖4 詳細給出了螺栓力的計算流程。

圖4 計算流程圖Fig. 4 Calculation flow chart

2.1 確定載荷作用區域和轉動軸

設備底座外輪廓被視為載荷直接作用區域。在縱向彎矩作用下，基座的轉動軸垂直于長條形基座的縱軸（長條方向），在橫向彎矩作用下，基座的轉動軸平行于長條形基座的縱軸（長條方向）。轉動軸位于設備外輪廓線形成的區域形心位置，或按照設備實際受力確定的位置，如圖5 和圖6所示。

2.2 確定受力的螺栓

對于每條連續梁，受載荷直接作用的2 個螺栓間的梁段被視為第1 跨，依次向外的梁段被稱為第2 跨、第3 跨等。基于連續梁理論，第1 跨支座（即螺栓）受力最大，向外逐步折減，第3 跨后的支座受力較小，可忽略不計。因此，取載荷區域內部螺栓和區域外往外擴的2 個螺栓進行計算，并對受力螺栓沿縱向進行編號（圖5）。

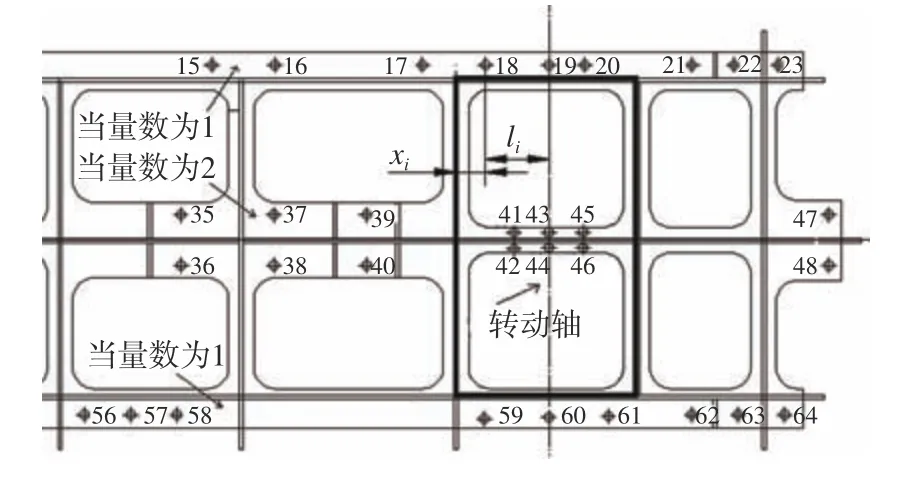
圖5 縱向彎矩作用時xi 的示意圖Fig. 5 Schematic of xi under longitudinal bending moment

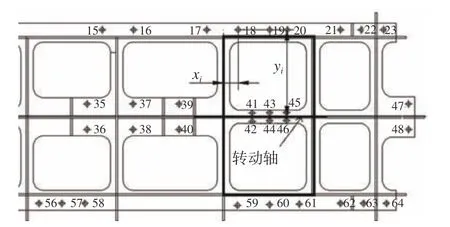
圖6 橫向彎矩作用時xi 與yi 的示意圖Fig. 6 Schematic of xi and yi under lateral bending moment

2.3 量取螺栓位置

如圖5 所示，確定第j 條梁上第i 個螺栓到設備外輪廓線區域形心所在縱軸的縱向距離li（單位：mm），以及第j 條梁上第i 個螺栓到縱向彎矩加載區（設備）邊界的縱向距離xi（單位：mm）。對于受到的橫向彎矩作用，還需確定第j 條梁上第i 個螺栓到彎矩作用區域MPC 中心的橫向距離yj（單位：mm），如圖6 所示。

2.4 分配載荷到每條梁上

基于上述3 個假設，將長條形公共基座沿橫向分為不相關的若干條連續梁，再按照各載荷作用下梁的變形特點，將作用在設備上的載荷按照縱向彎矩、拉力和橫向彎矩分配到每條梁上。

1） 縱向彎矩的分配。

首先，將彎矩分配到各梁上（式（1）），然后，再根據每條梁上力矩的平衡確定各螺栓的受力。

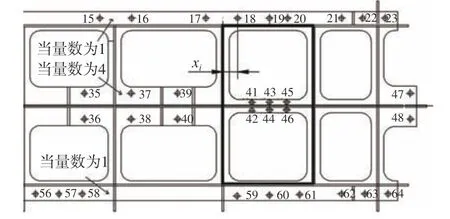
圖7 拉力作用下xi 的示意圖Fig. 7 Schematic of xi under tensile force

3） 橫向彎矩的分配。

首先，將彎矩按照轉動分配到各梁上，將每條梁視為受到拉力或壓力的作用，然后，根據受拉力作用梁上力的平衡，確定各螺栓的受力以及每條梁上螺栓到彎矩作用區域MPC 中心的橫向距離yj。彎矩作用計算公式為

2.5 計算載荷分配系數

根據彎矩和力的平衡，計算載荷分配系數。

1） 縱向彎矩作用。

需要說明的是，對于每條梁加載區域內中間螺栓（圖7 中的19，60，43，44 號螺栓）的xi，由于受到兩側力的作用，應考慮適當縮短。對于1 排螺栓，乘以0.67 的距離調整系數（如圖7 中的19，60 號螺栓）；對于2 排螺栓，則乘以0.8 的距離調整系數（圖7 中的43，44 號螺栓）。

2.6 單項載荷下的螺栓受力計算

將每條梁所分配的力再分配到梁的承載螺栓上，計算每個螺栓的受力Fi。

1） 縱向彎矩作用。

處于設備外輪廓區域形心處的螺栓內力很小，可以忽略不計，故取為0。計算承載螺栓的受力，即

2.7 螺栓的合力計算

合成每個螺栓在拉力、橫向彎矩與縱向彎矩作用下的受力。當外力作用于一點時，螺栓在各分力作用下的受力按照受拉為正，受壓為負進行相加，如式（9）所示。

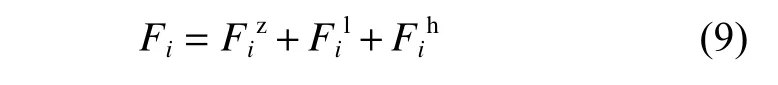
當多組設備同時受力及載荷作用于基座的多個位置時，可按上述方法分別計算出每個外力單獨作用下承載螺栓的內力，再按受拉為正，受壓為負的原則疊加每個螺栓在外力作用下的受力。

3 算 例

3.1 基座參數及載荷

3.2 有限元解

如圖3 所示，建立長條形基座的有限元模型，運用本文所提有限元計算方法對算例的基座進行分析，分別計算縱向彎矩、拉力、橫向彎矩與組合載荷，結果如圖8～圖11 中的實線所示。

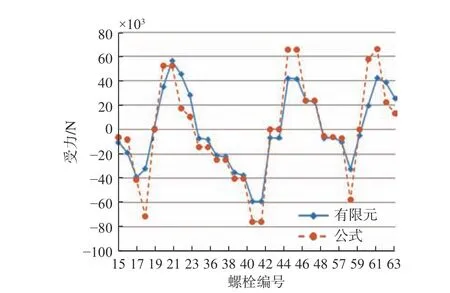
圖8 縱向彎矩作用下的螺栓受力Fig. 8 Mechanical behaviors of bolt under longitudinal bending moment

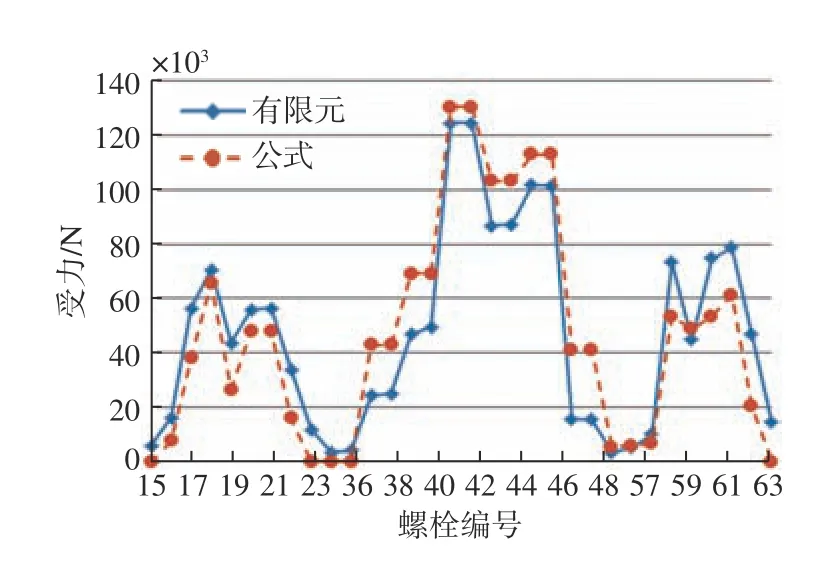
圖9 拉力作用下螺栓受力Fig. 9 Mechanical behaviors of bolt under tensile force

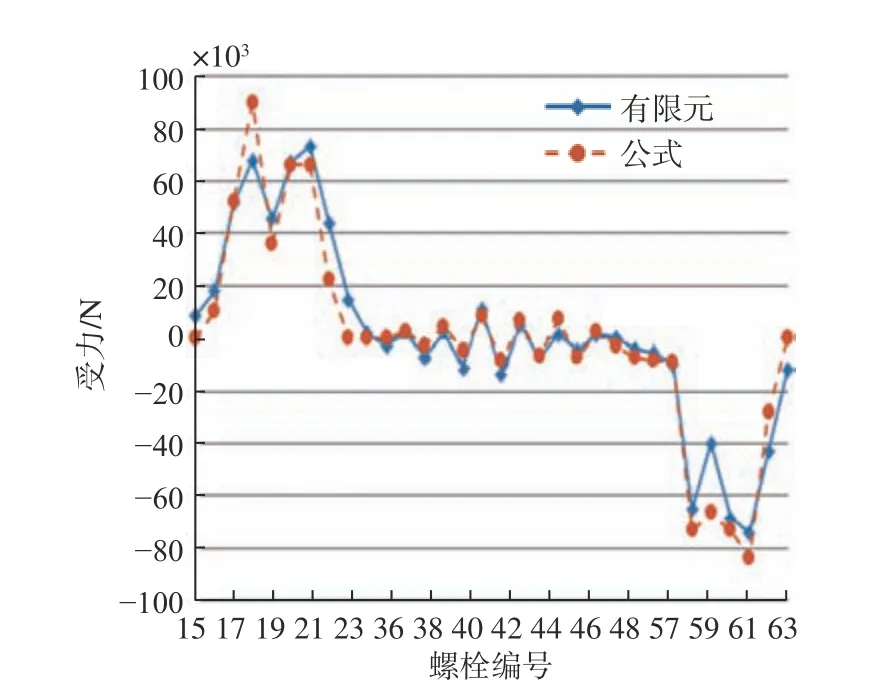
圖10 橫向彎矩作用下的螺栓受力Fig. 10 Mechanical behaviors of bolt under lateral bending moment

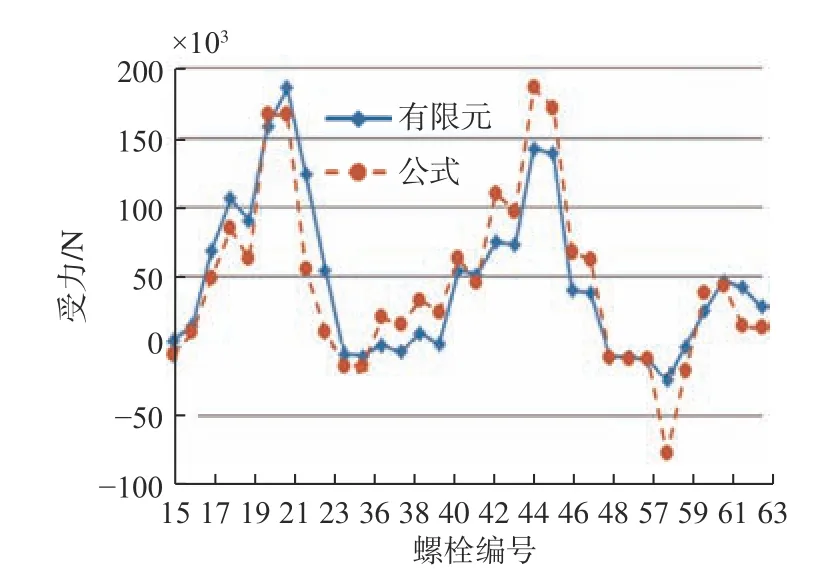
圖11 組合載荷作用下的螺栓受力Fig. 11 Mechanical behaviors of bolt under combined loading

3.3 近似解

將組合載荷分解為縱向彎矩、拉力與橫向彎矩并分別進行計算。對于縱向彎矩的作用，先確定轉動軸位置及螺栓分布位置，如圖5 所示；根據梁的總當量數，確定每條梁上的縱向彎矩；確定主要承載螺栓及其到設備外輪廓線區域形心所在縱軸的縱向距離li和到縱向彎矩加載區（設備）邊界的縱向距離xi；按照式（4）計算分配系數；按式（6）計算螺栓的受力并與有限元結果進行對比，如圖8 所示。

對于拉力、橫向彎矩及3 種載荷的組合作用，計算過程與此類似，這里不再贅述，具體結果如圖9～圖11 所示。

對各種載荷作用下長條形基座螺栓群螺栓的受力分布分析表明，本文所提公式的計算值與有限元模擬結果相差較小，公式計算精度較高。

4 結 語

針對多組設備長條形基座的螺栓群受力問題，本文梳理了采用有限元方法分析螺栓群受力的步驟及需要考慮的方面。在多個長條形基座有限元分析的基礎上，提出了一套求解長條形基座在縱向彎矩、拉力、橫向彎矩及其3 種載荷的組合作用下計算螺栓群受力的實用方法和公式。通過多個算例的應用，結果表明所提方法具有較好的理論和應用價值，其中近似方法不需復雜的有限元建模，尤其適用于基座的初步設計和優化，同時也可應用于基座支撐結構的強度校核。