基于COMSOL 的組合空腔結(jié)構(gòu)聲學覆蓋層的聲學性能分析

柯李菊，劉成洋，方智*

1 華中科技大學 船舶與海洋工程學院，湖北 武漢 430074

2 中國艦船研究設(shè)計中心，湖北 武漢 430064

0 引 言

聲學覆蓋層是一種吸聲能力很強的潛艇隱身結(jié)構(gòu)，主要用于覆蓋殼體，抑制殼體振動并吸收敵方主動聲吶信號，降低潛艇的聲反射強度，以減小被探測距離[1-3]。目前，聲學覆蓋層已經(jīng)專用化，在潛艇殼體的特定區(qū)域或頻段需要針對性地敷設(shè)不同種類的聲學覆蓋層，由此要求聲學覆蓋層的材料及內(nèi)部聲學結(jié)構(gòu)的設(shè)計必須多樣化。現(xiàn)有的含空腔聲學覆蓋層主要作為吸聲結(jié)構(gòu)，內(nèi)部腔形結(jié)構(gòu)多為簡單且規(guī)則的形狀（例如圓柱形、球形、錐形或者喇叭形），其與均勻無腔覆蓋層相比，吸聲效果較好[4]。含空腔聲學覆蓋層除具有良好的吸聲性能外，還兼有一定的隔聲性能。當將空腔結(jié)構(gòu)引入隔聲結(jié)構(gòu)中時，與不含空腔結(jié)構(gòu)的聲學覆蓋層相比，其隔聲效果得到了較大改善，但仍存低頻隔聲效果不好且在靜水壓力下會產(chǎn)生較大變形等問題[5]。

在現(xiàn)有空腔諧振型聲學覆蓋層的專利和文獻中，多數(shù)針對圓柱形和指數(shù)形空腔進行研究。劉國強等[6]使用COMSOL 有限元仿真軟件計算了橢球形空腔聲學覆蓋層的吸聲特性，分析了穿孔率、材料厚度以及材料參數(shù)對吸聲性能的影響規(guī)律，指出空腔穿孔率越大，聲學覆蓋層的吸聲性能或隔聲性能越好，但耐壓性能越差；聲學覆蓋層厚度越大，其吸聲性能和隔聲性能越好。周江龍等[7]使用COMSOL 軟件對圓柱形空腔聲學覆蓋層隔聲量進行了仿真計算，結(jié)果表明，在相同穿孔率下，較大直徑的圓柱空腔隔聲效果更好。張沖等[8]使用COMSOL軟件計算了球形空腔聲學覆蓋層在靜水壓力下的吸聲特性，指出隨著靜水壓力的增大，聲學覆蓋層的吸聲效果會變差。趙穎坤等[9]基于彈性體和黏彈性體的波傳遞理論，分析了水中蜂窩夾層結(jié)構(gòu)的隔聲性能，指出蜂窩夾層結(jié)構(gòu)的隔聲性能比打孔橡膠夾層結(jié)構(gòu)和均質(zhì)橡膠結(jié)構(gòu)的性能要好。唐世灝等[10]采用有限元方法研究了蜂窩空腔覆蓋層的隔聲性能，分析了蜂窩結(jié)構(gòu)的胞元壁厚度和夾角以及材料參數(shù)對隔聲量的影響，指出胞元壁厚越小，即空腔占比越大，聲學覆蓋層的隔聲效果越好。

繼含單一形狀的空腔（單腔結(jié)構(gòu) ）聲學覆蓋層后，組合形狀的空腔（組合空腔結(jié)構(gòu)）覆蓋層概念被提出。商超等[4]基于有限元法研究了組合空腔結(jié)構(gòu)的覆蓋層吸聲特性，結(jié)果表明，其吸聲特性明顯優(yōu)于具有相同穿孔率的單腔結(jié)構(gòu)。Zhong等[11]提出一種新型空腔結(jié)構(gòu)的聲學覆蓋層，即倒錐形空腔結(jié)構(gòu)，將其吸聲系數(shù)曲線與等容圓柱體空腔結(jié)構(gòu)的聲學覆蓋層的吸聲系數(shù)進行了對比，發(fā)現(xiàn)該聲學覆蓋層在低于5 000 Hz 頻率范圍內(nèi)的吸聲性能得到了提高。然而，對于組合空腔結(jié)構(gòu)的覆蓋層在隔聲性能方面的應(yīng)用及其研究鮮見報道。目前對于含空腔結(jié)構(gòu)的聲學覆蓋層的研究方法有2 種：一是對于黏彈性介質(zhì)中波傳播特性的解析法[12]，二是有限元法[13-15]。對于幾何形狀較復(fù)雜的聲學結(jié)構(gòu)，較難得到解析解，故多采用有限元方法進行研究。陶猛和卓琳凱[14]采用波導(dǎo)有限元方法分析了組合型圓臺空腔吸聲覆蓋層的聲學特性。陳文炯和劉書田[15]采用有限元法研究了空腔形狀與聲學性能參數(shù)之間的關(guān)系。

針對單腔結(jié)構(gòu)在低頻吸聲性能較差且受壓后變形較大的問題，本文擬提出一種圓臺組合空腔結(jié)構(gòu)，使用COMSOL 軟件對其隔聲、吸聲和耐壓性能進行仿真分析。首先，介紹使用COMSOL 軟件建立組合空腔結(jié)構(gòu)的聲學覆蓋層物理模型以及計算其隔聲和吸聲性能的方法，并將仿真結(jié)果與實驗測量結(jié)果進行對比，以驗證COMSOL 軟件的適用性和準確性。然后，使用COMSOL 軟件分析空腔幾何尺寸對聲學材料的隔聲、吸聲和耐壓性能的影響，提出一種在圓臺組合空腔四周均勻布置圓柱小孔的混合空腔結(jié)構(gòu)，并仿真分析小孔尺寸對材料聲學性能和耐壓性能的影響規(guī)律。最后，對得到的規(guī)律進行總結(jié)，為聲學覆蓋層內(nèi)空腔結(jié)構(gòu)的設(shè)計提供理論依據(jù)。

1 物理模型與方法

1.1 隔聲量和吸聲系數(shù)的計算

由于空腔結(jié)構(gòu)在聲學覆蓋層內(nèi)周期性均勻分布，排列形式一般是四邊形或三角形，因此采用周期性邊界條件，可以只研究1 個單胞單元內(nèi)的聲波傳播規(guī)律，來代替無限大聲學覆蓋層。為了便于研究，長方體或正棱柱體形成的單胞單元均可簡化為圓柱體單元，對于軸對稱的空腔結(jié)構(gòu)，可以使用二維模型代替三維模型，進而降低計算成本。簡化的聲學覆蓋層二維軸對稱模型結(jié)構(gòu)示意圖如圖1 所示。

本文主要研究組合空腔結(jié)構(gòu)聲學覆蓋層的隔聲和吸聲性能。簡化的圓臺組合腔型聲學覆蓋層單胞二維有限元模型如圖2 所示，采用COMSOL軟件模擬水聲管測量聲學覆蓋層的隔聲量和吸聲系數(shù)，在水聽器1 處測得的聲壓為 p1，水聽器2 處測得的聲壓為 p2，水聽器3 處測得的聲壓為 pt。水聽器1 與水聽器2 之間的距離為d，根據(jù)國標GB/T 18 696.2—2002 規(guī)定，各水聽器的位置均有相應(yīng)的計算公式。采用聲-彈性波交互物理場，將聲學材料域設(shè)置為固體力學模塊，而空腔內(nèi)的空氣域和水聲管中的水域被設(shè)置為壓力聲學模塊。在聲波入射端施加平面波聲源，在聲波透射端添加完美匹配層（PML）邊界條件，模擬無反射端邊界條件。

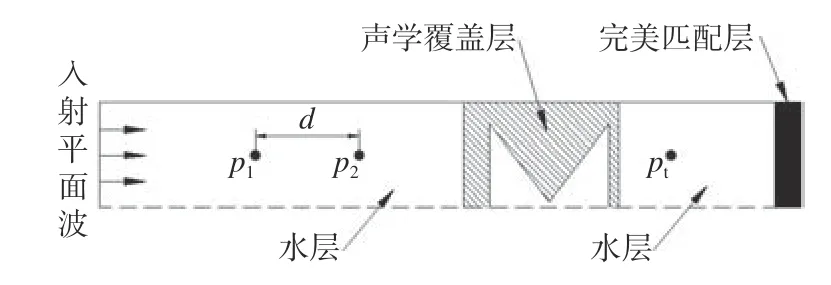
圖2 簡化的組合空腔結(jié)構(gòu)聲學覆蓋層有限元模型Fig. 2 Simplified FE model of the anechoic layers with combined cavity structure

根據(jù)樣品的聲壓反射系數(shù) Rre，求得測試樣品的吸聲系數(shù) α為

1.2 模型有效性驗證

圓柱形空腔聲學覆蓋層的聲學有限元分析技術(shù)比較成熟。為了驗證本文中采用COMSOL 軟件計算隔聲量方法的有效性，參照文獻[16-17]，選取厚度為40 mm 的帶圓柱空腔的覆蓋層結(jié)構(gòu)，計算其隔聲量曲線，并分別與文獻[16]的仿真結(jié)果和文獻[17] 的實驗結(jié)果進行對比。圓柱空腔高為20 mm，直徑為15 mm，覆蓋層單胞模型直徑為28.2 mm。隔聲材料的物理參數(shù)為：楊氏模量E=1.8 MPa，泊松比 ν=0.499 76， 密度 ρ=1 000 kg/m3，損耗因子 η=0.15。提取水聲管中3 個傳聲器位置的聲壓值 p1， p2和 pt，并根據(jù)傳遞函數(shù)法計算樣品的隔聲量。本文仿真計算結(jié)果與文獻[16] 結(jié)果的對比如圖3 所示。由圖可見，本文計算值與文獻[16]的結(jié)果吻合較好；與文獻[17]實驗結(jié)果的變化趨勢相同，但數(shù)值存在一定的差異。其原因可能是實驗測量過程中無反射端的設(shè)置與仿真計算中的設(shè)置不一致，也有可能是實驗過程中存在水聲管壁與隔聲材料和水介質(zhì)的耦合效應(yīng)，而在仿真計算中未考慮此效應(yīng)所致。而空腔型式的改變并未影響仿真計算方法的準確性，因此可以使用COMSOL 軟件進一步仿真計算組合空腔結(jié)構(gòu)聲學覆蓋層的隔聲量。

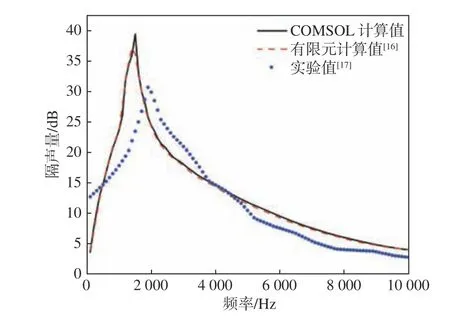
圖3 隔聲量的有限元仿真結(jié)果與文獻結(jié)果的對比Fig. 3 Results comparison between FE simulation and Reference[16-17] of sound transmission loss

為了驗證采用COMSOL 軟件計算吸聲系數(shù)的有效性，選取厚度為30 mm 的均勻無腔覆蓋層；隔聲層為橡膠材料，參數(shù)與前文所述相同；鋼背襯厚度為5 mm，材料物理參數(shù)為：楊氏模量E=2.07×105MPa，泊松比ν =0.3， 密度ρ =7 800 kg/m3。吸聲系數(shù)的COMSOL 計算值與文獻[18]的解析結(jié)果的對比如圖4 所示。由圖可見，兩者結(jié)果吻合較好，驗證了采用COMSOL 軟件計算組合空腔結(jié)構(gòu)聲學覆蓋層吸聲系數(shù)的有效性。

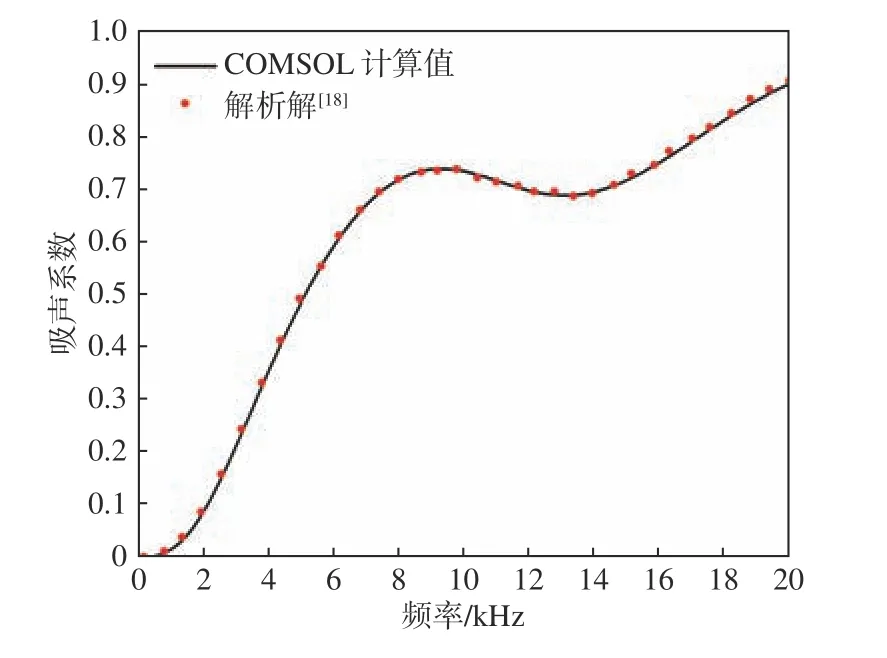
圖4 吸聲系數(shù)的有限元仿真結(jié)果與解析結(jié)果對比Fig. 4 Results comparison between FEM and analytical solution of the sound absorption coefficient

1.3 變形量的計算

在計算受壓變形量時，同樣利用COMSOL 軟件進行建模，將聲學覆蓋層下端設(shè)置為固定邊界，三維模型的周期性邊界條件轉(zhuǎn)化為二維軸對稱模型的法向量位移為零的邊界，覆蓋層模型上端為載荷邊界。本文采用模型最大壓縮變形量來簡單衡量聲學覆蓋層的耐壓性能。

1.4 組合空腔結(jié)構(gòu)與傳統(tǒng)空腔結(jié)構(gòu)對比

傳統(tǒng)空腔結(jié)構(gòu)主要包括球形、圓錐形、圓柱形等，本文研究的組合空腔由上、下圓臺組成，結(jié)構(gòu)示意圖如圖5 所示。為了體現(xiàn)組合空腔結(jié)構(gòu)在隔聲性能上的優(yōu)越性，選取3 種穿孔率相同的空腔結(jié)構(gòu)（圓柱形、球形和圓臺組合型）計算其隔聲量，計算結(jié)果對比如圖6 所示。由圖可見，組合空腔結(jié)構(gòu)的隔聲效果整體比傳統(tǒng)空腔結(jié)構(gòu)的隔聲效果更好。

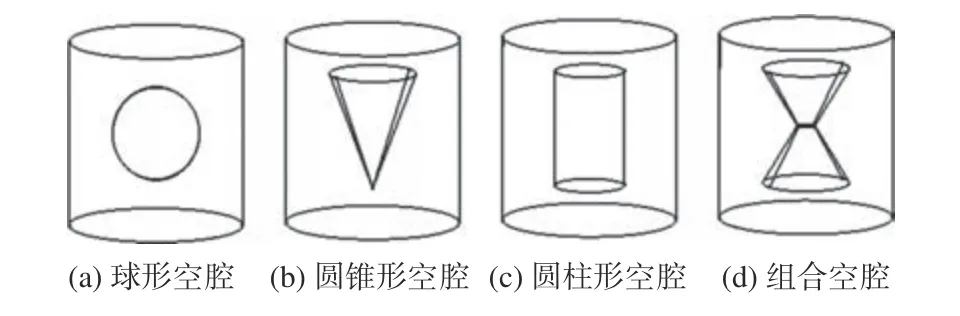
圖5 傳統(tǒng)空腔結(jié)構(gòu)與組合空腔結(jié)構(gòu)示意圖Fig. 5 Schematic diagram of traditional cavity structures and combined cavity structures

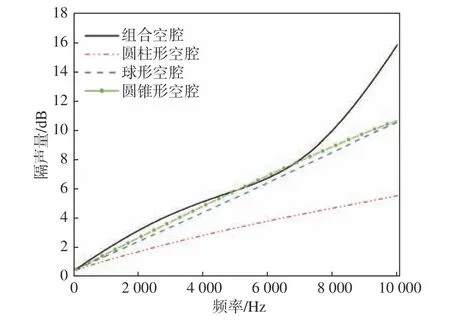
圖6 不同空腔結(jié)構(gòu)的隔聲量Fig. 6 The sound transmission loss of different cavities structures

2 組合空腔結(jié)構(gòu)幾何尺寸對聲學和耐壓性能的影響

2.1 組合空腔結(jié)構(gòu)大半徑與單胞半徑之比的影響

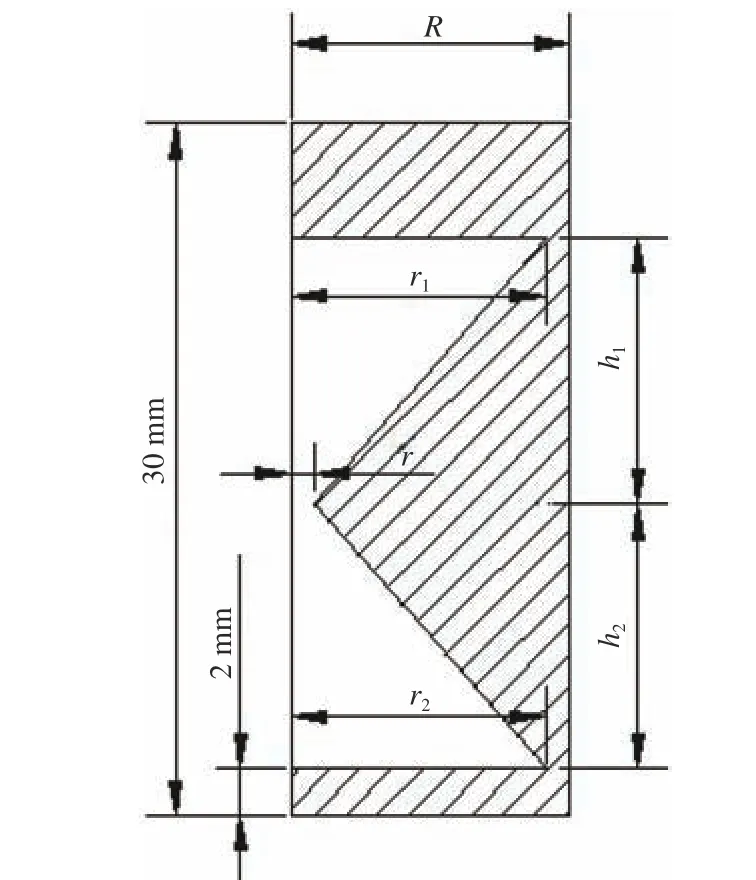
圖7 組合空腔結(jié)構(gòu)聲學覆蓋層有限元模型Fig. 7 FE model of anechoic layers with combined cavity structure

組合空腔結(jié)構(gòu)聲學覆蓋層單胞有限元模型如圖7 所示。由圖可見，組合空腔結(jié)構(gòu)由上、下2 個對稱的圓臺形空腔組成，圖中陰影部分為橡膠域，空白部分為空氣域。聲學覆蓋層厚度為30 mm，上、下各預(yù)留一定厚度的封孔層。聲學覆蓋層單胞半徑為 R，上、下圓臺空腔大半徑分別為r1和 r2， 小半徑為 r。上、下圓臺空腔高度分別為h1= h2= 11.5 mm。保 持圓臺小半徑為 r=1 mm不變，改變隔聲材料的單胞半徑R 及圓臺空腔大半徑 r1和 r2，分析其對隔聲量和吸聲系數(shù)的影響。再取上、下圓臺大半徑相等，分別為r1=r2=6,7,8,9,10,11 mm，相應(yīng)地聲學覆蓋層單胞半徑分別取為R=7,8,9,10,11,12 mm。通過仿真計算分析組合圓臺空腔大半徑與聲學覆蓋層單胞半徑之比不同時的隔聲量、吸聲系數(shù)及其在3 MPa 靜水壓力下的變形量，結(jié)果分別如圖8～圖10 所示。

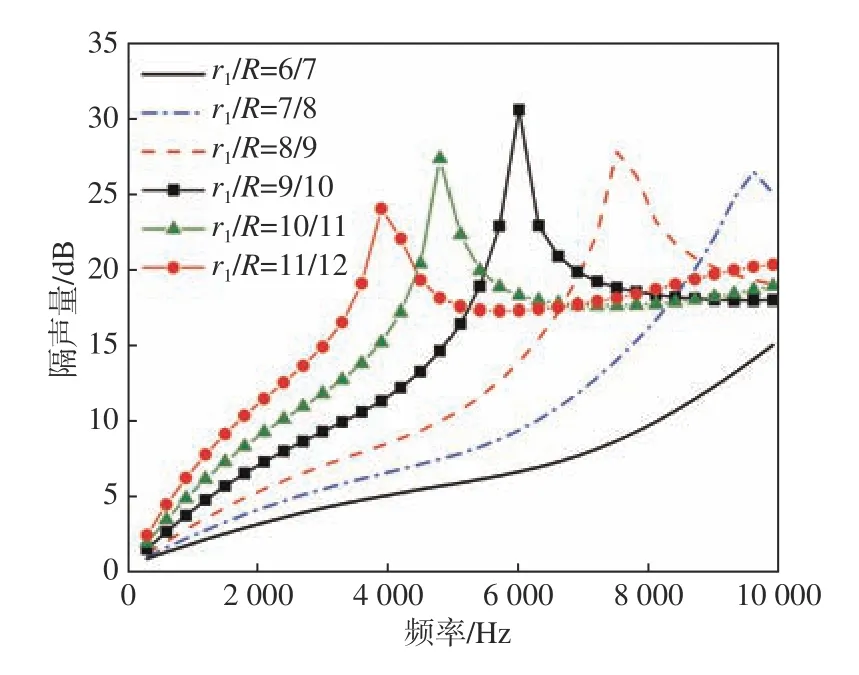
圖8 不同空腔大半徑與單胞半徑比下的隔聲量Fig. 8 The sound transmission loss under different r1/R

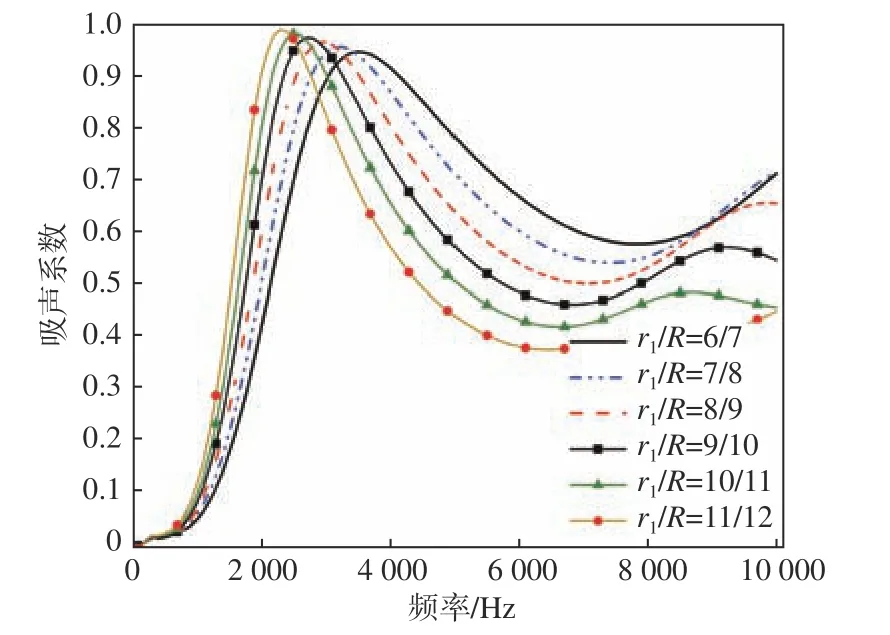
圖9 不同空腔大半徑與單胞半徑比下的吸聲系數(shù)Fig. 9 The absorption coefficient under different r1/R

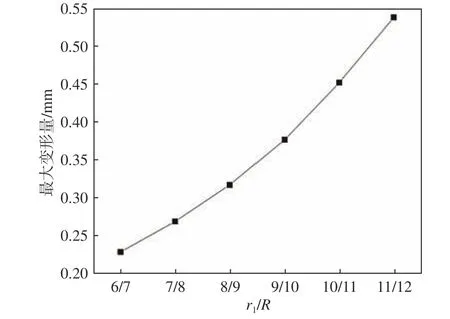
圖10 不同r 1/R的組合空腔結(jié)構(gòu)在3 MPa 靜水壓力下的變形量Fig. 10 Deformation of combined cavity structure with different r1/R under 3 MPa hydrostatic pressure

由圖8～圖10 可以看出，隨著 r1/R的增大：1）組合空腔結(jié)構(gòu)的整體隔聲效果變好，并會逐漸出現(xiàn)隔聲量峰值，且峰值頻率向低頻移動；2）吸聲系數(shù)峰值頻率向低頻移動，中、高頻的吸聲效果變差。但 r1/R越大時，空腔穿孔率越大，組合空腔結(jié)構(gòu)聲學覆蓋層的耐壓性能越差，在3 MPa 靜水壓力下的變形量越大。

2.2 組合空腔結(jié)構(gòu)大半徑的影響

減小聲學覆蓋層的空腔穿孔率可以改善其耐壓性能，但隔聲性能會受影響。在固定聲學覆蓋層單胞體積的基礎(chǔ)上，即保持R=11 mm，r=1 mm不變，改變組合圓臺空腔大半徑，分別取r1=r2=6,7,8,9,10,11 mm，分析聲學覆蓋層隔聲和吸聲性能的變化趨勢，得到的隔聲量變化曲線和吸聲系數(shù)變化曲線如圖11 和圖12 所示。

圖11 組合空腔結(jié)構(gòu)體積不同時的隔聲量Fig. 11 The sound transmission loss with different volumes of the combined cavity structure

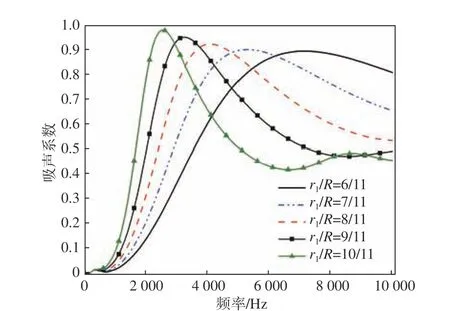
圖12 組合空腔結(jié)構(gòu)體積不同時的吸聲系數(shù)Fig. 12 The absorption coefficient with different volumes of the combined cavity structure

由圖中可以看出，當單胞體積固定時，增大圓臺大半徑r1，空腔體積變大，導(dǎo)致穿孔率增大，隔聲量曲線和吸聲系數(shù)曲線中的峰值頻率都逐漸減小，峰值不斷增大，整體隔聲性能增強，但中高頻的吸聲性能變差。

2.3 單胞半徑的影響

在固定空腔體積的基礎(chǔ)上，即 r1=r2=10 mm，改變單胞半徑，分別取 R=11,12,13,14,15 mm，分析聲學覆蓋層隔聲和吸聲性能的變化趨勢。圖13和圖14 為改變單胞半徑時的隔聲量和吸聲系數(shù)變化曲線。

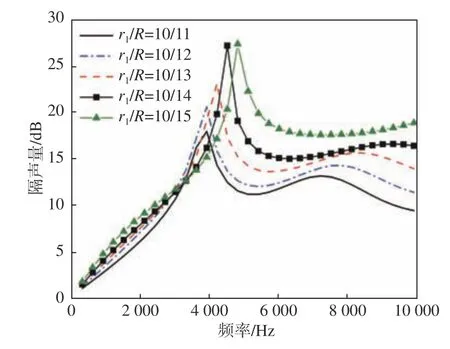
圖13 不同單胞半徑時的隔聲量Fig. 13 The sound transmission loss with different unit cell radii

圖14 不同單胞半徑時的吸聲系數(shù)Fig. 14 The absorption coefficient with different unit cell radii

由圖可以看出，當空腔體積固定時，增大單胞體積，即空腔體積占比減小時，隔聲量曲線中的峰值會向高頻移動，峰值增大，中、高頻范圍內(nèi)的隔聲性能改善；吸聲系數(shù)曲線中的峰值頻率也朝高頻移動，峰值基本不變，中、高頻范圍的吸聲性能也得到改善。

2.4 圓臺不對稱性的影響

分析組合空腔結(jié)構(gòu)中上、下圓臺不對稱時的聲學覆蓋層聲學性能和耐壓性能的變化規(guī)律。固定空腔下圓臺大半徑 r2=10 mm，上圓臺大半徑分別取 r1=6,7,8,9,10 mm時，仿真計算的隔聲量曲線和吸聲系數(shù)曲線分別如圖15 和圖16 所示。再固定上圓臺大半徑為 r1=10 mm，下圓臺大半徑r2=6,7,8,9,10 mm時，仿真計算得到的聲學性能曲線如圖17 和圖18 所示。分別改變上、下圓臺大半徑時，聲學覆蓋層在3 MPa 靜水壓力下的變形量如圖19 所示。

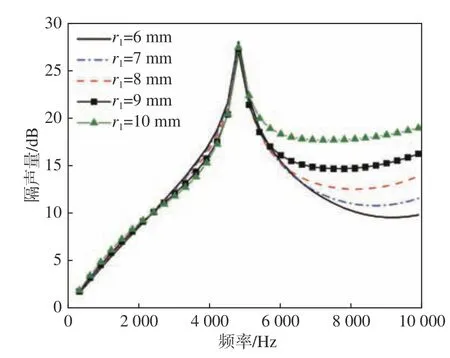
圖15 改變上圓臺大半徑 r1時的隔聲量Fig. 15 The sound transmission loss with different r1

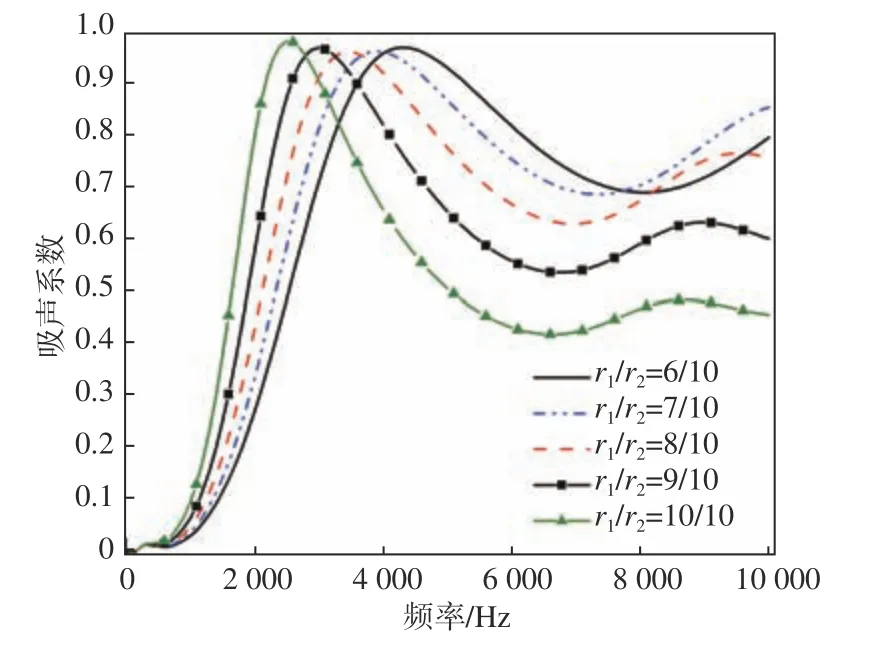
圖16 改變上圓臺大半徑 r1時的吸聲系數(shù)Fig. 16 The absorption coefficient with different r1

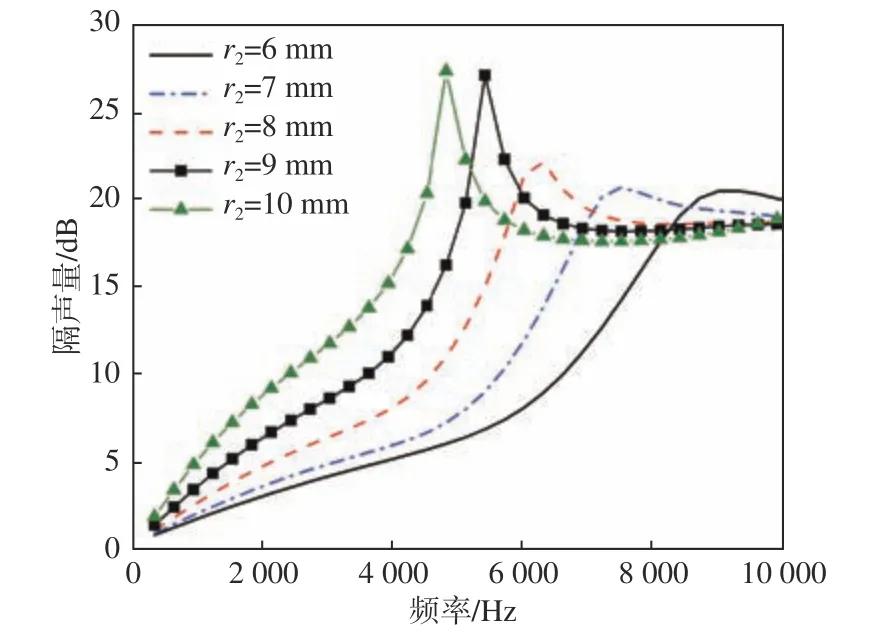
圖17 改變下圓臺大半徑 r2時的隔聲量Fig. 17 The sound transmission loss with different r2

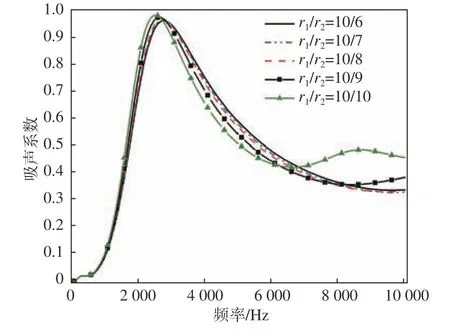
圖18 改變下圓臺大半徑 r2時的吸聲系數(shù)Fig. 18 The absorption coefficient with different r2

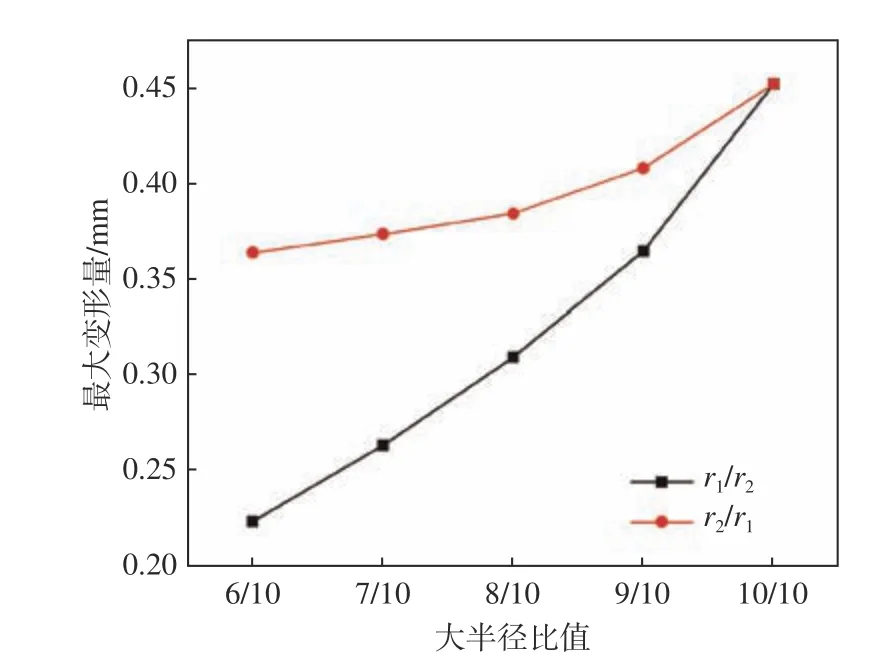
圖19 分別改變上、下圓臺大半徑時聲學覆蓋層在3 MPa 靜水壓力下的變形量Fig. 19 Deformation of anechoic layers with different r1 and r2 under 3 MPa hydrostatic pressure

由圖15～圖16 可以看出，當 r2固 定時， r1越大，中、高頻段的隔聲性能越好，隔聲量曲線的峰值頻率、峰值和低頻段隔聲量均沒有太大的變化。但隨著 r1的增大，吸聲系數(shù)峰值頻率逐漸朝低頻移動，中、高頻吸聲性能變差。

由圖17～圖18 可見，當 r1固 定時， r2增大，隔聲量曲線中出現(xiàn)明顯峰值；且 r2越大時，峰值頻率不斷減小，峰值不斷增大，但吸聲性能沒有明顯變化。這說明，靠近聲波入射端的空腔開口尺寸對隔聲量曲線中峰值頻率以及低于峰值頻率范圍內(nèi)的隔聲性能影響很小，隔聲量的峰值頻率和峰值更多地取決于遠離入射端的圓臺空腔的大半徑r2， 且 r2越大，峰值頻率越小，峰值越大，聲學覆蓋層在中、低頻的隔聲性能越好。而靠近入射端的空腔開口對吸聲性能的影響更大，開口越大，峰值頻率越小，遠離入射端的開口對吸聲性能的影響則不明顯。

由圖19 可以看出，隨著空腔體積的增大，聲學覆蓋層在3 MPa 靜水壓力下的變形量增大，且r1對 結(jié)構(gòu)耐壓性能的影響比 r2的大。這表明，靠近受壓面的一端開口越大，結(jié)構(gòu)的耐壓性能越差。在保證聲學覆蓋層的隔聲性能的基礎(chǔ)上，可以增大遠離聲波入射一側(cè)的空腔體積而減小靠近聲波入射一側(cè)的空腔體積，進而提高其耐壓性能。

3 圓柱小孔對聲學性能和耐壓性的影響

由前述分析可知，穿孔率越大，聲學覆蓋層的隔聲性能越好，但耐壓性能越差。因此，組合空腔結(jié)構(gòu)的設(shè)計應(yīng)兼顧隔聲性能和耐壓性能，根據(jù)需改善的頻率范圍合理設(shè)計組合空腔體積和空腔間距（即單胞的體積）。為了平衡空腔結(jié)構(gòu)的隔聲性能和耐壓性能，研究在前文的組合空腔結(jié)構(gòu)周圍增加1 組圓柱小孔時對聲學覆蓋層的隔聲、吸聲性能和耐壓性能的影響。

3.1 有/無圓柱小孔的影響

圖20 為在前文的組合空腔結(jié)構(gòu)四周增加圓柱小孔后的聲學覆蓋層結(jié)構(gòu)示意圖。小孔沿圓周分布，相鄰兩孔夾角為45°，小孔半徑為 r0=1 mm，高度為 h=3.5 mm，小孔距組合空腔中心線的距離為10 mm。聲學覆蓋層單胞體積和組合空腔結(jié)構(gòu)的體積均不變，分別計算添加圓柱小孔前、后組合空腔聲學覆蓋層的隔聲和吸聲性能，2 種結(jié)構(gòu)的隔聲量和吸聲系數(shù)比較曲線如圖21 和圖22所示。

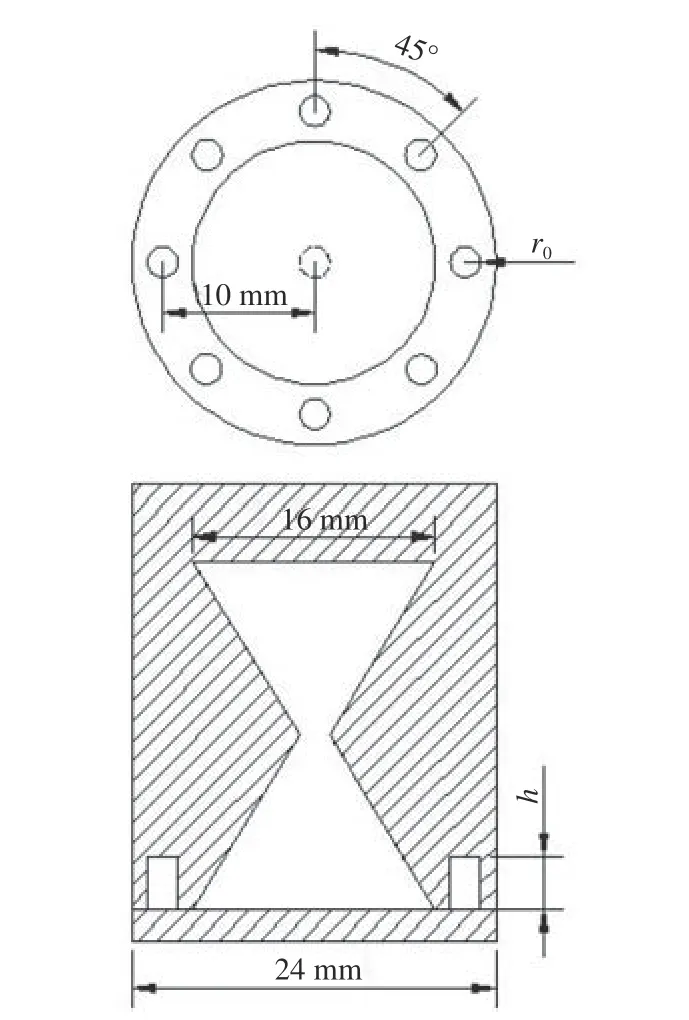
圖20 四周增加圓柱小孔后的聲學覆蓋層結(jié)構(gòu)示意圖Fig. 20 Schematic diagram of structure of anechoic layers adding cylindrical holes around

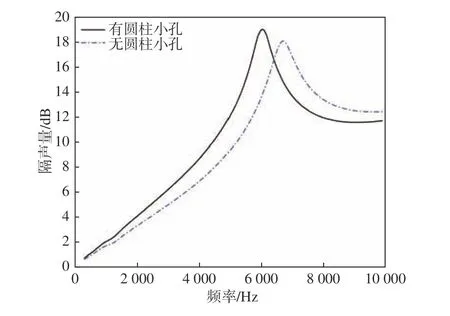
圖21 有/無圓柱小孔的組合空腔結(jié)構(gòu)隔聲量對比Fig. 21 Comparison of sound transmission loss related to combined cavity structures with/without cylindrical holes

圖22 有/無圓柱小孔的組合空腔結(jié)構(gòu)吸聲系數(shù)對比Fig. 22 Comparison of absorption coefficient of combined cavity structures with/without cylindrical holes

由圖可知，在固定聲學覆蓋層單胞體積和組合空腔體積的前提下，在原組合空腔四周增加一定數(shù)量的圓柱小孔能提高覆蓋層在低頻段的隔聲和吸聲性能，并且會使得峰值頻率向低頻移動，相較而言對隔聲性能的影響更為明顯。這是因為圓柱小孔增大了聲學覆蓋層中空腔的有效體積，尤其在遠離聲波入射方向的一側(cè)，即圖19 中的下圓臺大截面一側(cè)，圓柱小孔增大了下圓臺空腔的大半徑，進而使得隔聲量中的峰值頻率向低頻移動，且在低于峰值頻率范圍內(nèi)的隔聲性能變好。

3.2 圓柱小孔的高度和孔徑的影響

圓柱小孔個數(shù)固定為8 個，均勻分布，結(jié)構(gòu)示意圖如圖20 所示。改變圓柱小孔的高度和孔徑，分析其對聲學覆蓋層的隔聲、吸聲性能和耐壓性能的影響，計算結(jié)果分別如圖23～圖26 所示。

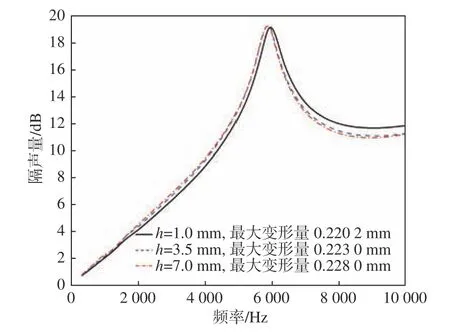
圖23 圓柱小孔的高度對隔聲量和耐壓性能的影響Fig. 23 Influence of the height of cylindrical holes on sound transmission loss and pressure resistance

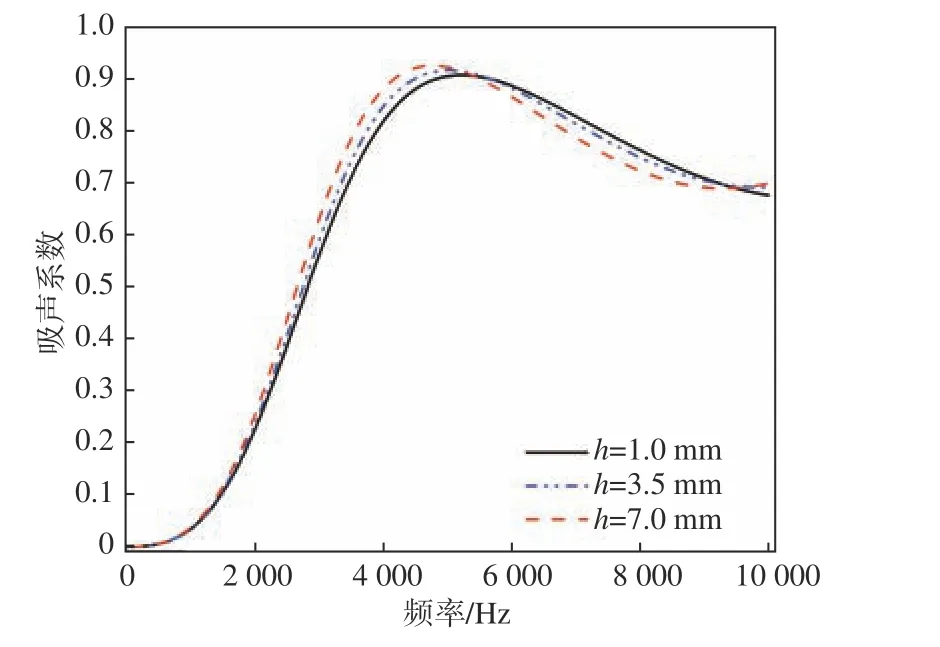
圖24 圓柱小孔的高度對吸聲系數(shù)的影響Fig. 24 Influence of the height of cylindrical holes on absorption coefficient

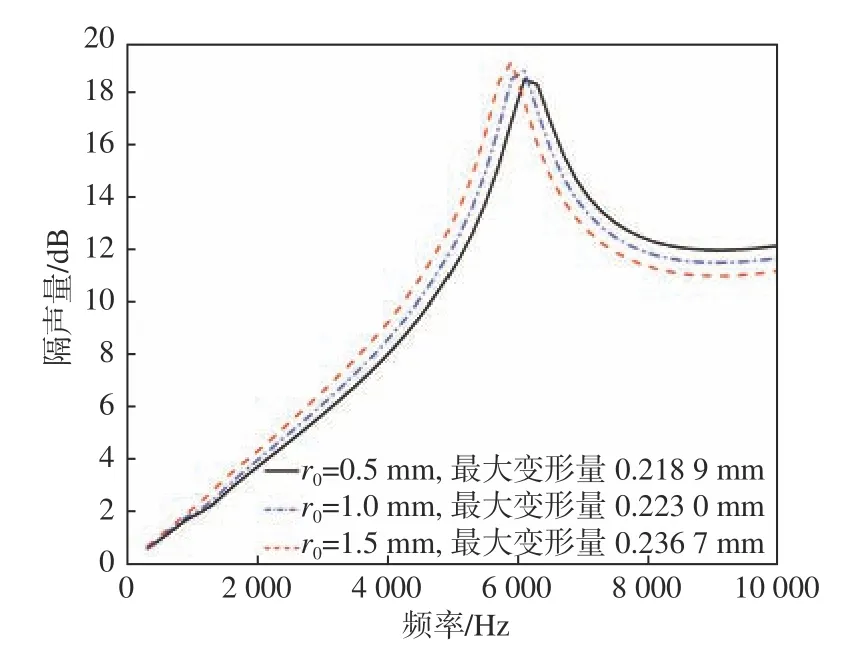
圖25 圓柱小孔的半徑對隔聲量和耐壓性能的影響Fig. 25 Influence of the radius of cylindrical holes on sound transmission loss and pressure resistance

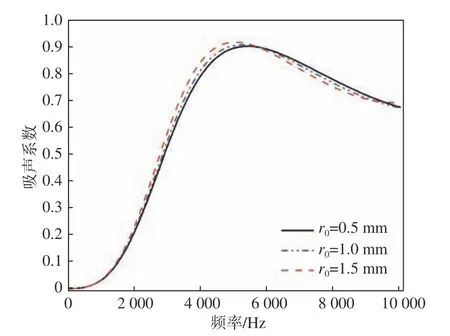
圖26 圓柱小孔的半徑對吸聲系數(shù)的影響Fig. 26 Influence of the radius of cylindrical holes on absorption coefficient

由圖可知，當圓柱小孔的半徑固定時，圓柱小孔的高度對隔聲和吸聲性能的影響均不大，對峰值之前的隔聲性能基本沒有影響。當圓柱小孔的高度固定時，圓柱小孔半徑增大，導(dǎo)致空腔的有效體積增加，因此隔聲性能在低頻段略有提升，隔聲量和吸聲系數(shù)的峰值頻率朝低頻移動少許。而圓柱小孔的半徑和高度變化時，聲學覆蓋層的最大變形量變化均不大，這說明圓柱小孔的體積變化對聲學覆蓋層的耐壓性能影響很小。

4 結(jié) 論

針對目前單一腔型聲學覆蓋層低頻隔聲性能以及耐壓性能較差的情況，本文采用COMSOL 有限元軟件建立圓柱空腔聲學覆蓋層的分析模型，通過與實驗測量結(jié)果對比，驗證了有限元分析方法的有效性，進而計算對比了組合空腔不同幾何尺寸下聲學覆蓋層的隔聲量、吸聲系數(shù)及其在3 MPa 靜水壓力下的最大變形量。得出以下結(jié)論：

1） 當組合空腔結(jié)構(gòu)為上、下對稱結(jié)構(gòu)和聲學覆蓋層單胞體積固定時，空腔部分圓臺的大截面面積越大，即穿孔率越大，隔聲量和吸聲系數(shù)中的峰值頻率越向低頻移動，且低頻段的隔聲效果更好；當組合空腔結(jié)構(gòu)的體積固定時，隨著聲學覆蓋層單胞體積的增大，即穿孔率降低，隔聲量和吸聲系數(shù)中的峰值頻率略微向高頻移動，中、高頻的隔聲量增大。

2） 當組合空腔中的上、下圓臺結(jié)構(gòu)為非對稱結(jié)構(gòu)時，聲學覆蓋層的隔聲性能更多地取決于遠離聲波入射端的圓臺大半徑，吸聲性能主要取決于靠近聲波入射端的圓臺大半徑，而靠近受壓一側(cè)的圓臺大半徑同樣對聲學覆蓋層的耐壓性能影響較大。

3） 在聲學覆蓋層單胞體積和空腔體積固定時，組合空腔四周布置一定數(shù)量的孔徑較小的圓孔，會提高聲學覆蓋層在低頻段的隔聲和吸聲性能，并且會使峰值頻率向低頻移動。小孔的高度和孔徑變化對隔聲和吸聲效果的影響不大。