豪華郵輪多航速興波阻力的船型優化

劉鑫旺，萬德成*

1 上海交通大學 船舶海洋與建筑工程學院，上海 200240

2 上海交通大學 海洋工程國家重點實驗室，上海 200240

3 上海交通大學 船海計算水動力學研究中心，上海 200240

0 引 言

近20 年來，我國船舶工業取得了日新月異的發展，造船技術水平不斷提高，已成功設計和建造了大量除豪華郵輪外所有類型的船舶。豪華郵輪因其個性化的內裝設計、陸地化的層次布局和多樣化的娛樂設施，被賦予了“海上移動城市”之美譽，是國際造船業公認的集高技術、高附加值和高可靠性于一身的“三高”船舶，導致其設計建造難度大、造價高。許多發達國家造船業的重心已在向豪華郵輪傾斜，歐洲一些國家憑借其技術、經驗和設備供應等方面的優勢，在豪華郵輪的設計與建造領域一直保持著領先地位。

2018 年11 月6 日，中國船舶工業集團有限公司與美國嘉年華集團、意大利芬坎蒂尼集團正式簽訂了13.5 萬總噸的Vista 型郵輪建造合同，標志著中國首艘具有世界先進水平的大型郵輪進入實質性建造階段，為我國自主開展豪華郵輪的設計與建造提供了基礎。

與常規船舶相比，豪華郵輪的結構通常具有以下特點：

1） 主尺度：型寬較大而型深較小，方形系數較小，水線以下尖瘦；

2） 艏艉結構：為方艉和彎鼻型球艏，艏柱前傾且有外飄；

3） 推進方式：多采用電力驅動，無主機與推進軸系，機艙占用空間較小，振動噪聲低；

4） 美學設計：水線以上部分講究自然美觀，上、下結構需直線對齊。

然而，由于豪華郵輪船型的特殊性（例如商用建造模型不易得到），在豪華郵輪的水動力性能，特別是阻力性能優化方面，相關的文獻較少[1-3]，所能獲取的文獻多為針對豪華郵輪航線和布置等方面的優化[4-7]。因此，考慮到豪華郵輪的上述特點，以及我國對其設計建造方面的強烈需求，需進一步開展基于水動力性能的豪華郵輪設計與優化研究。

本文擬基于自主開發的船型優化設計軟件OPTShip-SJTU，以某豪華郵輪為原始船型，采用自由變形（free-form deformation，FFD）方法，對船艏、水線、船艉等位置進行局部變形；通過基于Neumann-Michell（NM）勢流理論的興波阻力求解器NMShip-SJTU 進行阻力評估，結合優化算法得到不同航速下興波阻力系數最優的船型；通過采用經過廣泛驗證的高精度黏流求解器naoe-FOAMSJTU，對優化船型做進一步的驗證。

1 豪華郵輪的特點及其優化設計要求

豪華郵輪不僅是旅游運輸工具，更是旅游休閑之處，這就決定了其在安全、舒適、環保節能等方面比一般類型船舶的要求更高。

1） 安全性。基于豪華郵輪大型化的發展以及船上人員眾多的考慮，安全方面的問題越來越受到重視。據統計，豪華郵輪事故大多由破損和失火導致。因此，豪華郵輪的設計不僅要滿足《國際海上人命安全公約》（SOLAS）[8]的要求，還要滿足《安全返港規則》（SRtP）[9]的要求。根據要求，在一定的安全界限內發生火災或浸水事故時，船舶應能依靠自身動力安全返港。在此過程中，旅客能安全地處于“安全區域”內并能滿足基本生活需求；當事故超出安全界限時，重要系統能運行3 h 以保證有序撤離。可見，充足的動力是必需的。從水動力性能的角度考慮，在船舶以某設計航速航行時，若其受到的阻力較小，無疑會節省動力，以備不時之需。

2） 舒適性。豪華郵輪的舒適性主要是通過控制船舶的振動和噪聲實現。豪華郵輪因多采用電力驅動，無主機和推進軸系，故機艙產生的振動和噪聲較小。此外，水動力噪聲也不容忽視，例如船舶以中、高航速航行時興起的自由表面波在其生成與傳播的過程中會產生水動力噪聲，從而影響到郵輪的觀賞性和舒適性。

3） 環保節能。為了構建“綠色”海洋，現代郵輪均具有“清潔”、“綠色”船級符號。國際海事組織（IMO）近年來相繼推出了用于控制CO2排放的船舶能效設計指數（energy efficiency design index，EEDI）等規則，這些規則將在很大程度上影響豪華郵輪的設計。針對船舶的安全、環保、能效及船員的健康防護等，EEDI 提出了更高的要求。對船舶各水動力性能而言，阻力性能無疑對EEDI的影響最大。

因此，對于豪華郵輪的型線設計，針對阻力性能的船舶設計與優化尤其重要。

隨著CFD 技術和船舶CAD 技術的發展，可利用基于數值模擬的船型優化設計徹底擺脫傳統的船型設計模式。該技術是以船舶一項或多項水動力性能最優作為設計目標，在給定的約束條件和構型設計空間內，通過CFD 數值評估技術和現代最優化技術來實現船舶水動力構型的優化求解，最終獲得給定條件下水動力性能最優的船型。

在基于水動力性能的豪華郵輪型線優化過程中，至關重要的一環是水動力性能評估。根據流體力學中對流體黏性處理方法的不同，水動力性能的評估方法可分為2 大類：基于無黏假設的勢流方法和考慮流體黏性的黏流方法。勢流方法雖然假設流體無黏，與實際有一定的差異，但對某些特定條件下的問題，例如利用摩擦阻力與興波阻力疊加代替船舶總阻力，此方法在船舶設計領域仍被廣泛采用，并且其最大的優勢是在維持較高精度的前提下計算時間與資源消耗極少，可見該方法非常適用于豪華郵輪的初步設計與優化階段。而考慮黏性的全流場CFD 方法可以更加真實地還原流場情況，方便獲取流場所有信息，且具有較高的精度和可信度，可以輔助或在某種程度上替代昂貴的船模試驗，但相比勢流方法，黏流方法的計算時間和資源消耗巨大。

國內外在船型優化與應用方面已取得巨大進展[10-15]：優化船型從簡單的數學船型、標模過渡到實際應用船型；船型變換方法多樣；目標函數大多為興波阻力、總阻力、船艉伴流均勻度等；水動力性能評估方法主要包括經驗公式、勢流方法、黏流RANS 方法等；優化算法包含基于梯度的優化算法和基于生物進化的智能優化算法等；近似模型主要為Kriging、神經網絡等。然而，國內大多是借助商用軟件來構建優化平臺或評估水動力性能。因此，根據豪華郵輪型線優化的需要，自主開發優化平臺，進行基于船舶水動力性能的型線優化迫在眉睫。

對豪華郵輪的阻力優化可通過勢流理論方法來高效評估興波阻力，所得優化船型的興波阻力可顯著降低，進而減小豪華郵輪的總阻力。同時，其還將減小船舶的自由表面興波進而降低水動力噪聲，提高觀賞性和舒適性。此外，由于豪華郵輪在使用上的特殊性，其不像一般船舶那樣需要根據設計航速來設計建造，而應考慮郵輪上游客的觀賞需要。例如，當欣賞優美的海上風光以及海底生物時，需要以較低的航速航行，反之，則需略微提高航速以節省更多時間。因此，在豪華郵輪的設計建造過程中，不能只針對單一航速，而要進行多航速下的性能優化。

本文擬首先采用OPTShip-SJTU 軟件，對某豪華郵輪在2 個航速（Fr = 0.171 15和0.209 18）下的興波阻力系數進行優化，然后采用FFD 方法進行船型變換，阻力性能則由興波阻力求解器NMShip-SJTU 進行評估，最后采用多目標遺傳算法得到優化船型，并進行基于黏流的CFD 評估以驗證優化結果的可靠性，以為同類型豪華郵輪的優化設計提供參考。

2 船型優化軟件模塊與原理

上海交通大學船海計算水動力學研究中心（CMHL）基于C++語言與OpenFOAM 開源平臺，自主開發了一款船型優化設計工具OPTShip-SJTU，該軟件不依賴其他商用軟件，集成了船型變換模塊、水動力性能評估模塊、近似模型構建模塊和優化求解模塊，可實現船型的自動優化設計。軟件框架如如圖1 所示。

圖1 船型優化軟件OPTShip-SJTU 框架Fig. 1 Framework of OPTShip-SJTU hull form optimization software

2.1 船型變換模塊

Sederberg 和Parry[16]最早提出了FFD 方法，該方法類似于彈性物體外殼受到外力變形時，嵌入在其中的幾何實體也隨之變形。運用FFD 方法，按類似的步驟對三維實體進行變形：首先，將待變形區域用一控制體包圍，這相當于將變形物體嵌入到彈性控制體中；然后，通過移動控制體的控制頂點改變控制體形狀，該步驟相當于彈性體受到外力而發生變形；最后，處于控制體中的待變形物體隨著控制頂點的移動而發生相應的變形。圖2 所示為FFD方法示意圖。其中圖2（a）中黃色的頂點構成初始控制體，圖2（b）中粉色的頂點及黃色的頂點分別代表移動控制點和固定控制點。通過該操作，可實現船體艏部的變形。

FFD 方法的控制體一般可選取為長方體，在其長、寬、高三個方向上分別均勻分布(l+1)，(m+1)，(n+1)個控制點，用其將待變形區域包圍。控制體內待變形物體的坐標包含全局坐標（O-XYZ）和局部坐標（O'-STU），如圖3 所示。

圖2 FFD 方法示意圖Fig. 2 Schematic diagram of FFD method

圖3 FFD 方法的全局坐標與局部坐標系示意圖Fig. 3 Schematic diagram of global and local coordinate systems of FFD method

通過下式的函數關系，將控制體內待變形物體的全局坐標與控制頂點的全局坐標建立聯系：

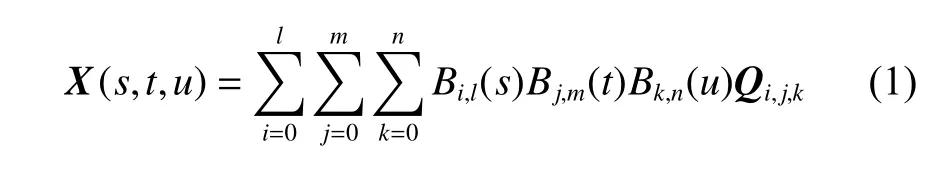
式中：Qi,j,k為控制頂點的全局坐標；X 為控制體內待變形物體的全局坐標；（s，t，u）為控制體內待變形物體的局部坐標；Bi,l，Bj,m，Bk,n分別為l，m，n 次Bernstein 多項式。以求和號下的第1 項 Bi,l(s)為例，Bernstein 多項式定義為

由式（1）可看出，全局坐標用于描述物體的空間幾何位置，可表示為控制頂點與Bernstein 多項式乘積的線性疊加，因此移動控制頂點時，待變形物體的全局坐標也會發生改變；而局部坐標則表示控制體內待變形物體與控制體頂點的相對位置，一旦控制體給定，控制體內待變形物體的局部坐標（s，t，u）就已確定，變形過程中也不會發生改變。

如果控制體為規則的長方體，且控制頂點在3 個方向均勻分布，則可采用式（3）快速求解局部坐標：

式中：X0為控制體原點的全局坐標；S，T，U 分別為控制體長、寬、高方向上的矢量，如圖3 所示。任意一點的局部坐標（s，t，u）都可以通過式（4）求得：

控制體頂點的全局坐標可按式（5）求得：

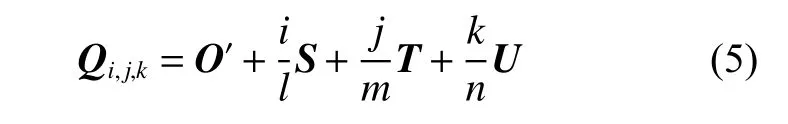
式中： i=0,1,...,l; j=0,1,...,m; k=0,1,...,n。

本文計算模型是根據初始圖形交換規范（initial graphics exchange specification，IGES）文件轉換成船體面網格，然后利用FFD 方法進行船型變換而得。當移動FFD 方法中的控制體頂點時，將上述計算得到的局部坐標（s，t，u）以及新的控制頂點坐標代入式（1），即可得到控制體內任意一點變形后的全局坐標。

2.2 水動力性能評估模塊

采用NM 方法求解船舶興波問題。該方法由Noblesse 等[17]于2013 年提出，是對Neumann-Kelvin（NK）理論進行改進而得到的一種方法。在NK 理論中，流場任意一點的速度勢都可以表示為船體濕表面積分與沿船體水線積分之和。其中，沿船體水線積分是求解難點，因為需要考慮自由面影響并計算速度勢偏導數。NM 理論則引入了協調流動模型和波浪函數，其通過一系列的數學變換，消去了NK 理論中沿船舶水線的積分項。在NM 理論中，只需計算船體濕表面上的積分，就可以得到流場內任意點的速度勢。圖4 所示為NM 理論坐標示意圖。

圖4 NM 理論坐標示意圖Fig. 4 Schematic diagram of coordinate system of NM theory

NM 理論是基于格林函數法來求解速度勢，是將邊值問題轉化為積分問題進行求解。根據格林函數第二公式，可得邊界積分表達式

進一步地，根據協調線性流動模型，式（10）經數學推導，可進一步簡化為

利用上述公式，可進一步對船舶靜水興波阻力、升沉、縱傾以及自由面波高等進行預報。采用該方法不僅能準確預報船舶阻力變化趨勢，而且計算耗時短、空間少，非常適用于船型優化。因此，本文將采用基于上述方法和利用C++語言自主開發的興波阻力求解器NMShip-SJTU 來作為興波阻力數值計算的工具。

2.3 響應函數近似模型構建模塊

采用上述船舶水動力勢流理論和船型設計數值計算量較大，而在船型設計中引入試驗設計方法則可在保證一定精度的前提下大幅提高優化效率。

試驗設計（DoE）方法是一種從數理統計學的角度確定試驗設計方案的方法，其可在保證樣本群體精度的同時降低設計方案樣本數。圖5 所示為以x1，x2為設計變量的均勻分布試驗設計、隨機拉丁超立方試驗設計和優化拉丁超立方試驗設計。從中可以看出，優化拉丁超立方試驗設計的均勻性和正交性更優，可以更好地提高計算效率。因此，本文采用優化拉丁超立方試驗設計方法選取新船型方案樣本。

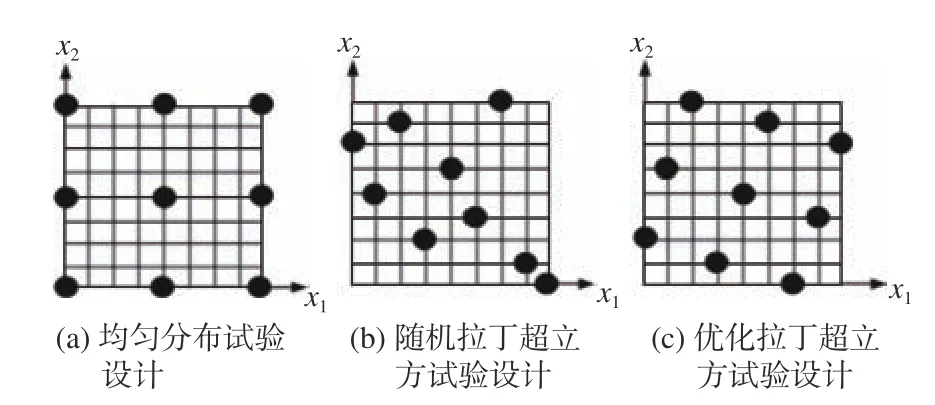
圖5 不同試驗設計方法的均勻性和正交性示意圖Fig. 5 Schematic diagram of uniformity and orthogonality of different DoE methods

Kriging 近似模型[15]是地質統計學建立的近似函數的主要模型，最初主要用于采礦領域，隨后被逐漸用于多個領域。該模型是一種針對變量的空間相關性，對變量取值進行無偏、最優估計的方法。其基本思想是：未知點的值是其周圍臨近點值的平均，權值為與未知點的距離。從插值角度而言，是對空間分布的數據求線性最優、無偏內插估計的一種方法。Kriging 模型具有較好的適應性，可廣泛應用于對低階和高階非線性函數的逼近。對試驗設計中選取的新船型興波阻力逐一計算后，根據Kriging 近似模型，即可建立表示興波阻力系數等水動力參數與船型參數之間關系的響應函數，本文將該響應函數用于船型優化。

2.4 優化求解模塊

當只有一個目標函數時，可以找到一個全局最優解，該解要優于其他解。而當多個目標共存時，目標之間往往會存在沖突，很難找到一個解來使所有目標同時最優。因此，有一種多目標優化方法，其實質是：在不讓任何一個目標變差的前提下，至少使一個目標變優，這種多目標優化方法稱為基于Pareto 前沿的優化。對于多目標優化問題，通常存在一個解集，特點是其中所有的解都不再擁有Pareto 優化的余地，這種解集稱作Pareto 最優解集。

非支配排序遺傳算法（non-dominated sorting genetic algorithm，NSGA）[18]采用非支配分層方法，可以使性能更優的個體有更大的概率存活，其適應度共享策略可防止“超級個體”過度繁殖而早熟收斂。但是，NSGA 仍存在缺乏精英策略、計算復雜等問題。NSGA-II 引進了精英策略，將優良的父代個體直接保存到子代種群，能防止因優良個體丟失而導致的算法效率下降；另外，采用擁擠度比較算子來評估個體周圍的群體密度，并同時根據非支配排序和擁擠度選取合適的個體，在含精英策略的條件下可保證種群的多樣性。因此，NSGA-II 成為目前最流行、最可靠的多目標遺傳算法之一，也是本文采用的多目標興波阻力優化算法。

3 豪華郵輪型線優化實例

3.1 優化問題的建立與求解

本文針對首個國產的13.5 萬噸級Vista 型豪華郵輪在2 個航速（Fr=0.171 15 或0.209 18）下的興波阻力進行了優化設計，船體形狀和主尺度分別如圖6 和表1 所示。

圖6 豪華郵輪外形主視圖Fig. 6 Main view of luxury cruise ship

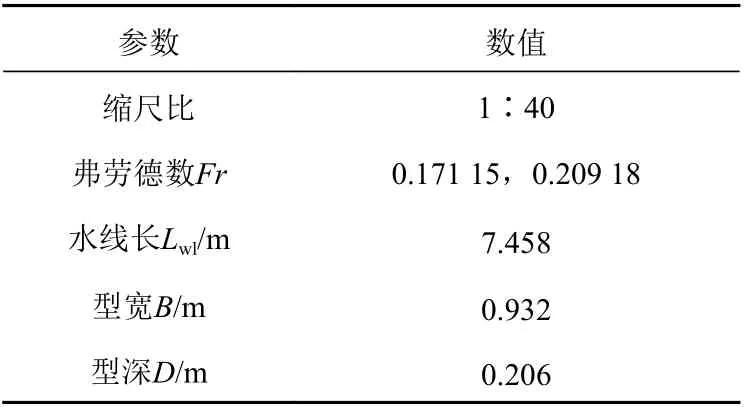
表1 豪華郵輪主尺度Table 1 Main dimensions of luxury cruise ship

優化時，需精心考慮幾何重構區域，以便對船舶興波阻力產生影響。考慮到局部變形范圍限制對整船濕面積大小的影響不大，以興波阻力代表總阻力來對目標進行船型優化。選取2 個航速下的興波阻力系數Cw作為目標函數，按上節所述原理對其進行多目標優化，目標函數定義為：

采用FFD 方法對船艏、艉進行幾何重構，如圖7所示。圖中3 個長方體框分別代表3 個FFD 變形區域，紅色線條為水線。下面，將予以詳細說明。

圖7 豪華郵輪FFD 變形框示意圖Fig. 7 Schematic diagram of FFD lattices of luxury cruise ship

首先，因豪華郵輪的彎鼻球鼻艏可以降低興波阻力，故可以優化其形狀，在球艏區域設置一控制體，實現球艏在長度、寬度和高度上的變化。但由于該豪華郵輪吃水較淺，導致球艏有一小部分在水面上，為確保主尺度中的水線長不變，需要限制球艏處的進水點不變，這就要求該變形框在沿船長及吃水方向的控制點要有所限制，以防止進水點在船長方向上的變化，以及由于吃水方向的變形導致原進水點進入水下而使水線面變小。

其次，雖然進水點限制不變，但因入流段水線寬可以變值，即整個艏部水線（平行于舯體前）都可以在船寬方向上發生變化，因此可在近水線處設置變形框，但要保證型寬不變。

最后，在船艉去流段（平行于舯體后）設置變形框，按吃水方向移動近水線的控制點及2 個橫剖面在船寬方向的控制點來綜合改變艉部橫剖線的UV 度。

各控制體內均勻分布了控制頂點。圖8 中，綠色控制點為固定控制點，紅色控制點為移動控制點，設計變量總數為7 個，如表2 所示。表中，7 個設計變量的變化范圍為無因次化位移。

采用優化拉丁超立方試驗設計方法，在由7 個設計變量所形成的樣本空間中生成均勻、正交的樣本點，總計280 個，不同設計變量在設計空間中的分布如圖9 所示。同時，通過FFD 方法變形得到280 個新船型，之后評估各新船型的興波阻力，最終，采用Kriging 模型構建近似響應函數曲面來代表目標函數與設計變量間之的關系。

圖8 船體各變形框FFD 控制頂點分布Fig. 8 Distribution of control points of FFD lattices

表2 優化算例定義Table 2 Definition of optimization case

圖9 不同設計變量在設計空間中的分布Fig. 9 Distribution of different design variables in design space

3.2 優化結果與分析

圖10 興波阻力系數Pareto 前沿Fig. 10 Pareto front of wave-making drag coefficient

采用多目標遺傳算法NSGA-II 搜索最優解，初始群體大小為200，交叉率0.8，變異率0.2，最大迭代次數400，最終獲得Pareto 前沿如圖10 所示。圖中，fobj1和fobj2分別為較低航速和較高航速的興波阻力系數值，藍色的星點構成優化算法獲得Pareto 前沿。從中可以看出，與單目標優化問題相比，多目標優化不再是尋求唯一最優解，而是一系列可行解的集合。Pareto 前沿形成了一個凸集，即相比Pareto 解，其不存在其他解，使得目標函數f1減小的同時f2也減小，或者f2減少的同時f1也減小。另外還可以看出，最優前沿的各優化船型在Fr=0.171 15 和0.209 18 時其興波阻力系數為負相關。本文選取Pareto 解集上的2 個可行解（OPT1 和OPT2），如表3 所示，對優化結果進一步進行分析與驗證。

圖11 所示為2 個優化船型與原始船型的橫剖線對比圖。從中可以看出，球艏部分與船艉部分變形的差異較大，入流段水線變化基本一致。

基于NM 理論，對比2 個優化船型（OPT1, OPT2）與原始船型的自由面興波，結果如圖12 所示。從中可以看出，由于球艏變形，導致優化船型在2 個航速下其船艏波的波峰和波谷均有所降低，其中OPT1 的優化效果更明顯。

為進一步驗證優化結果的可靠性，對原始船型和2 個優化船型分別在2 個航速下的靜水總阻力進行了評估，求解器采用基于OpenFOAM 平臺自主開發的黏性流動求解器naoe-FOAM-SJTU[19-20]。該求解器包含六自由度運動模塊和數值造波模塊，可以準確預報快速性、耐波性、推進性和操縱性等船舶水動力性能，并能給出精細的流場特征，其可靠性已在很多研究中[19-20]得到驗證。

表3 優化船型設計變量取值Table 3 Design variable values of optimal hulls

圖11 優化船型與原始船型型線對比Fig. 11 Comparison of hull lines between optimal and initial hulls

圖12 勢流評估下優化船型與原始船型自由面興波對比Fig. 12 Comparison of wave elevation between optimal and initial hulls by NMShip-SJTU

基于naoe-FOAM-SJTU 求解器，得到2 個優化船型與原始船型的自由面興波z、船體表面壓力p 分布對比如圖13 所示。從中可以看出：OPT1在船艏位置興波有所降低，艏部高壓區略降低；OPT2 主要在船的平行舯體位置興波有所降低，艏部高壓區降低明顯。

表4 和表5 所示分別為2 個優化船型與原始船型總阻力評估結果的對比。由表可見，基于勢流評估下得到的優化船型，其總阻力中的壓阻力均明顯下降，說明基于NM 理論評估得到的優化船型可靠；而在摩擦阻力幾乎不變的情況下，總阻力均較原始船型有所降低。實際上，本文利用勢流理論求解器時并未考慮黏性的影響，因此優化目標為不同航速下的興波阻力，從興波阻力的優化效果來看，優化幅度較大。與興波阻力對應的是黏流求解器求得的總阻力中的壓阻力成分，由壓阻力結果也可見其從側面反映出了基于勢流的優化效果。后續進行驗證時，可補充模型試驗驗證或其他商用軟件驗證來進一步說明本文方法的可靠性。上述結果表明，基于NM 理論的興波阻力優化可以得到總阻力性能更優的船型，相比基于黏流的CFD 評估，其優化更高效，具有較高的應用價值。

圖13 黏流評估下優化船型與原始船型自由面興波、船體表面壓力分布對比Fig. 13 Comparison of wave elevation and hull surface pressure distribution between optimal and initial hulls by naoe-FOAM-SJTU

表4 原始船型與OPT1 優化船型的總阻力對比（Fr = 0.171 15）Table 4 Comparison of total resistance between initial and OPT1 hulls at Fr = 0.171 15

表5 原始船型與OPT2 優化船型的總阻力對比（Fr = 0.209 18）Table 5 Comparison of total resistance between initial and OPT2 hulls at Fr = 0.209 18

4 結 語

本文采用船型優化軟件OPTShip-SJTU，對某豪華郵輪的阻力性能進行了優化。首先，結合豪華郵輪的特點和設計要求，分析了對船體進行合理變形來得到新船型的方法；然后，利用優化拉丁超立方試驗設計的結果，對各新船型采用NMShip-SJTU 求解器進行了興波阻力系數的計算；最后，通過建立的近似響應函數模型，利用NSGAII 優化算法對豪華郵輪在2 個航速下的多目標興波阻力系數進行優化并予以了進一步的驗證。結果表明，基于勢流理論評估對船舶靜水興波阻力性能進行優化的方法高效，其結果可采用黏流評估的結果予以驗證；OPTShip-SJTU 可廣泛應用于豪華郵輪實用船型的阻力性能優化，2 個計算航速下的總阻力減阻效果分別達0.65%和0.98%。基于豪華郵輪的實際需求和特點，后續還可考慮針對其上層建筑高、穩性差的穩性優化，針對美學需求的豪華郵輪外形主尺度優化，以及針對游客舒適性、方便游覽、防止暈船的耐波性優化等。