考慮勞動收入風險的多階段投資組合研究

（中南大學商學院，長沙 410083）

引 言

投資組合理論致力于解決財富在不同資產中最優配置的問題。Harry［1］的均值-方差投資組合模型成為單階段的投資組合選擇理論的基礎。但實際投資活動通常是多階段的，投資者需要根據現實情況不斷地調整投資策略，來實現自己的預期目標。 Duan 和 Ng［2，3］使用嵌入法和隨機線性控制法，提出了長期投資組合問題中均值-方差模型的有效投資策略。隨后，圍繞著長期多階段資產配置的研究大量展開［4-6］，但都是在完全市場條件下進行。因此，在不確定環境下的投資組合選擇問題已成為近年來研究的熱點。很多學者從現實出發，考慮了各種現實因素對資產配置的影響，如交易成本［7］、通貨膨脹［8］、投資者觀點［9］、破產約束［10］。

在現實資本市場中，投資者經常面臨著除所持有的風險資產自有風險以外的風險，背景風險便是其中一種不可忽視的風險，該風險是指不能在金融市場上通過資產組合配置來進行分散的風險［11］。 Jiang 等［12］、Li等［13］研究表明，投資者的勞動收入、創業收入等本身的不確定性因素也會沖擊長期投資組合的效用。勞動收入作為背景資產的一個重要組成部分，對投資者的長期投資組合的構建具有重要的影響。Palia等［14］利用微觀層面的數據，驗證勞動收入波動率與家庭股市參與和持股比例的關系。Bellalah等［15］進一步探討了勞動收入風險對資產配置的影響。宋煒和蔡明超［16］使用中國家庭金融調查數據進行實證研究，發現投資者的勞動收入不確定性會對股市參與度及風險資產的投資產生一定的影響。

由此可見，勞動收入風險會對投資者長期投資組合的構建產生一定的影響，但以往對離散時間下的不完全市場的研究卻忽視了這一重要因素。因此，本文在離散時間下的多階段均值-方差模型中，引入勞動收入風險，構建含有勞動收入風險的多階段均值-方差模型，然后利用改進的遺傳算法對該模型求解，并進行數值模擬，從而系統探討勞動收入風險的引入及其變動對長期多階段投資組合的影響。

1 考慮勞動收入風險的多階段均值-方差模型

1.1 模型的假設

為便于模型的建立，對關于考慮勞動收入風險的多階段投資組合決策過程做出以下假設：

勞動收入假設：與普通的金融資產不同，勞動收入是一種不可交易、不可對沖的非資本資產。目前對勞動收入的不確定性的量化方法可分為以下3類：（1）使用職業等代理指標來衡量收入不確定性，以Skinner［17］為代表；（2）采用與收入相關數據的方差和標準差等形式，代表人物有Carroll和 Samwick［18］；（3）采用問卷調查方式來獲取人們對勞動收入不確定性的感知程度，主要代表人物是 Guiso 等［19］。

本文參考Carroll和Samwick［18］對勞動收入的量化方法，假設勞動收入是隨機變量，其具有一個持久性的增長率，并且受到多樣化沖擊的影響，則勞動收入的變動過程為：

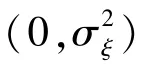
投資行為假設：整個投資過程中不會有額外的資金投入或抽出，投資者最終持有的資本市場獲得的財富只由最初的資金投資n次后獲得。另外，投資中不允許賣空行為。

資本市場假設：在整個交易過程中，不存在交易成本和稅收等費用，同時不受最小交易量的限制。

1.2 考慮勞動收入風險的多階段均值-方差模型

假定資本市場是由n種風險資產和1種無風險資產構成，風險資產的收益率隨機，無風險資產的收益率確定。投資者在0時刻開始投資，資本市場的初始投資財富為W0，共進行了T-1期的投資，在第t時期，無風險資產的收益率為，第i種風險資產的收益率為，投資者自身的勞動收入為Yt，用表示t時刻投資于風險資產i的比例，則t時刻投資于無風險資產的數量為1-是t時刻勞動收入中用以投資于資本市場的比例，本文中的t階段，是指t時刻到t＋1時刻這一時間段。投資者財富數量由勞動收入及資本市場上的金融財富構成，則投資者期末財富總額為：

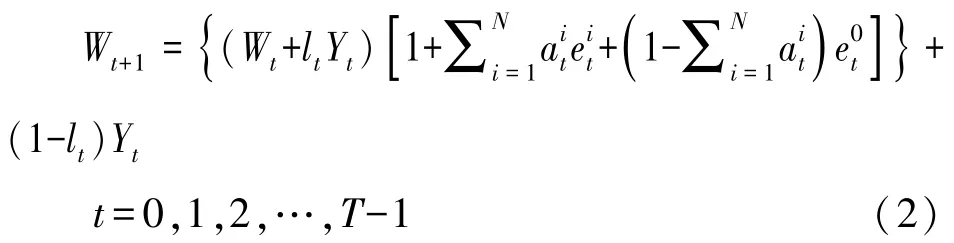
投資者的投資決策是以最大化終端財富的期望值、最小化終端財富的風險為目標，則含有勞動收入風險的多階段投資組合模型為：

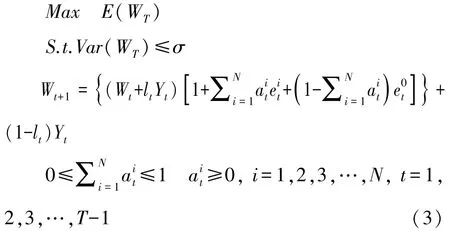
對于上述相互制約的雙目標規劃問題，不存在嚴格意義上的最優解。常用的方法是將多目標規劃問題轉化為單目標規劃問題進行求解。因此，本文引入風險厭惡系數ω，把目標模型轉化成以下模型：

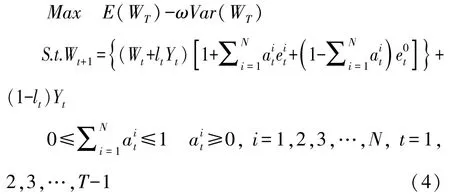
式中，ω（ω＞0）為投資者的風險厭惡系數，ω越大表示投資者風險厭惡程度越高。

綜上，含有勞動收入風險的多階段均值-方差模型為：

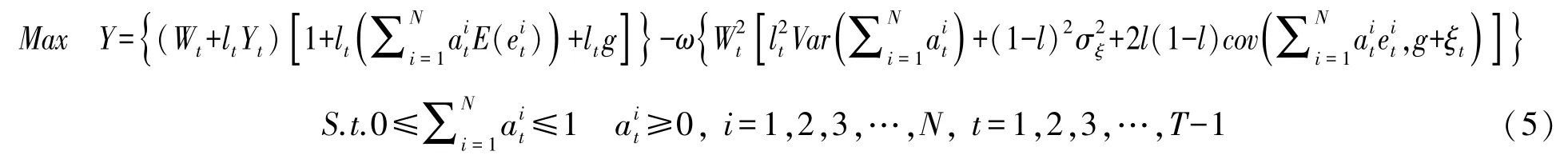
勞動收入風險是指投資者由于自身未來勞動收入的不確定而承受的風險。一般來說，勞動收入風險主要來自于以下兩個方面：勞動收入增長率的波動性和勞動收入與風險金融資產的相關性。具體來說，勞動收入風險在式（5）中表現為勞動收入增長率的方差和勞動收入與風險資產的協方差這兩個變量。

對以上模型進行求解，就可得到含有勞動收入風險的多階段均值-方差模型的每一階段最優的投資策略。

2 模型的求解

由于上述模型屬于動態規劃問題，很難求出解析解，一般采用遺傳算法來求解其最優的投資策略。遺傳算法是一種進化算法，基本原理是仿效生物界中的“物競天擇、適者生存”的演化法則，將問題參數編碼為染色體，再進行選擇、交叉以及變異等運算，最終生成符合優化目標的染色體。該算法在求解非線性、多目標等復雜系統優化問題上具有全局優化等優點，用于解決投資組合優化問題是十分有效的。因此，本文選擇遺傳算法來求解該模型。由于傳統的遺傳算法產生的初始種群會導致中心集聚現象，本文采用了Bermudez等［20］提出的對初始種群取對數然后標準化的方法，從而達到初始種群分布均勻的效果。

算法的步驟如下：

步驟1：初始化種群。設定遺傳算法相關參數，隨機初始化種群，按照式（6）對初始種群ui取對數、標準化：

步驟2：計算適應度。把目標函數作為個體的適應度函數。函數值越大的個體，適應度值越大，個體越優。適應度計算函數為：

步驟3：選擇操作。從舊群體中按照式（8）的概率選擇優良個體組成新的種群，以繁殖得到下一代個體。

其中，Fi為個體i的適應度值，N為種群個體數目。

步驟4：交叉操作。從種群中按照設置好的交叉概率Pc隨機選擇兩個個體，按照式（9）進行交叉操作：

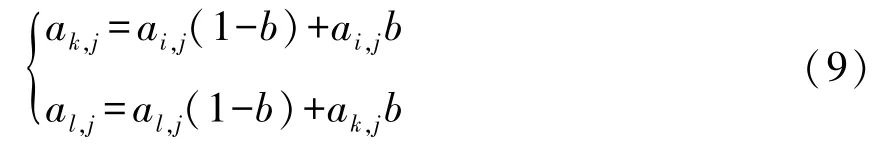
其中，b是區間［0，1］的隨機數。

步驟5：變異操作。按照變異概率對個體按式（10）進行變異，以產生更優秀的新個體。

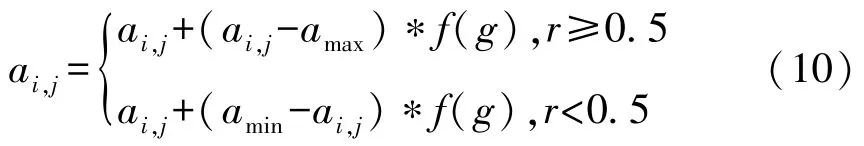
其中，amax是基因 ai，j的上界；amin是基因 ai，j的下界。

步驟6：根據最大迭代次數判斷終止與否，若達到最大迭代次數則輸出最優的結果，若未達到則返回到步驟2，重新計算。

3 勞動收入風險對多階段投資組合影響

3.1 勞動收入風險的引入對多階段投資策略的影響

為檢驗所提出模型的有效性，從而對勞動收入風險的引入及變動對多階段投資組合選擇的影響進行系統而細致的探討。本文使用實際的市場數據，采用改進的遺傳算法進行求解。

投資者從股票市場上選取4只股票，得到這4只股票2014～2016年收盤價數據，以1年為1個投資周期，即N＝4、T＝3，計算得到其年收益率及方差，相關數據如表1所示。投資者的風險厭惡系數為2，即ω＝2。投資者投資于以上4只股票和1只無風險資產國債，資本市場初始投資金額為1，初始勞動收入為1，連續進行3期的投資活動，并在每期期初調整各個資產的投資比例。無風險資產的收益率為0.02，此外，假設每期投資于資本市場的勞動收入比例為0.5，即lt＝0.5。

由 《中國勞動統計年鑒》的數據計算得，我國居民勞動收入年增長率均值約為0.15，居民勞動收入年增長率方差約為0.0029，勞動收入增長率與股票年收益率略微正相關，協方差為0.006。考慮到勞動收入增長率與風險資產的其他相關關系，還設置了協方差為-0.006和0的情況，即勞動收入風險分別與風險資產正相關、負相關和不相關。此外，勞動收入增長率數值為0.04、0.1和0.2，設置3組勞動收入增長率方差數據來表示勞動收入風險的變化，分別為0.0015、0.002和0.0025。

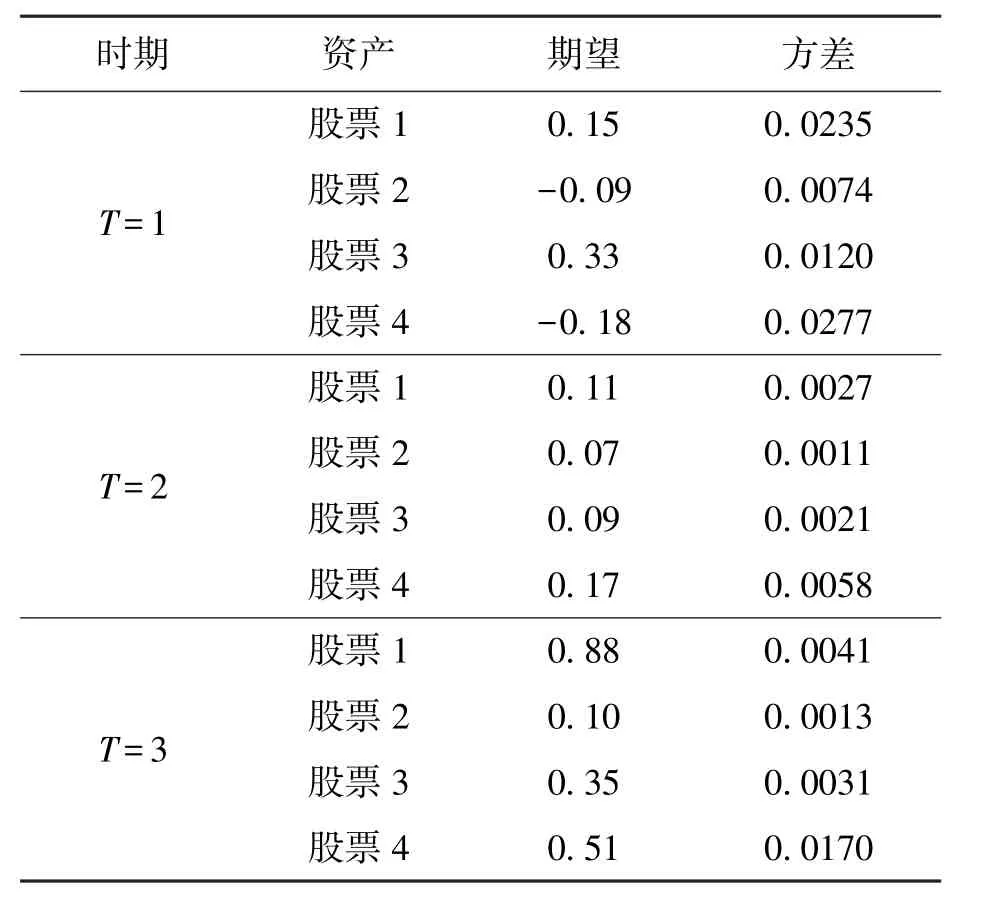
表1 股票的年收益率及方差

因為遺傳算法是一種隨機搜索方法，其最優解會隨著參數的變化而變化，我們取100個模擬值的平均數來解決這個問題。對于遺傳算法的相關參數設定，見表2。

表2 遺傳算法運行參數設定

檢驗所提出模型的有效性。使用改進的遺傳算法，考慮勞動收入增長率為0.1，勞動收入增長率與風險資產收益率正相關，勞動收入增長率方差為0.0015時，每一期投資組合的風險及收益。圖1（a～c）展示了每一期含有勞動收入風險的投資組合有效前沿（V-E）。 由圖1（a～c）可知，在考慮勞動收入風險時，投資組合的總風險隨著勞動收入風險的增加而增加，同時也表明隨著收益的增加，總風險也是逐漸增加的，這與投資活動中高收益高風險的原則是一致的，說明本文所提出的考慮勞動收入風險的多階段均值-方差模型是有效的。

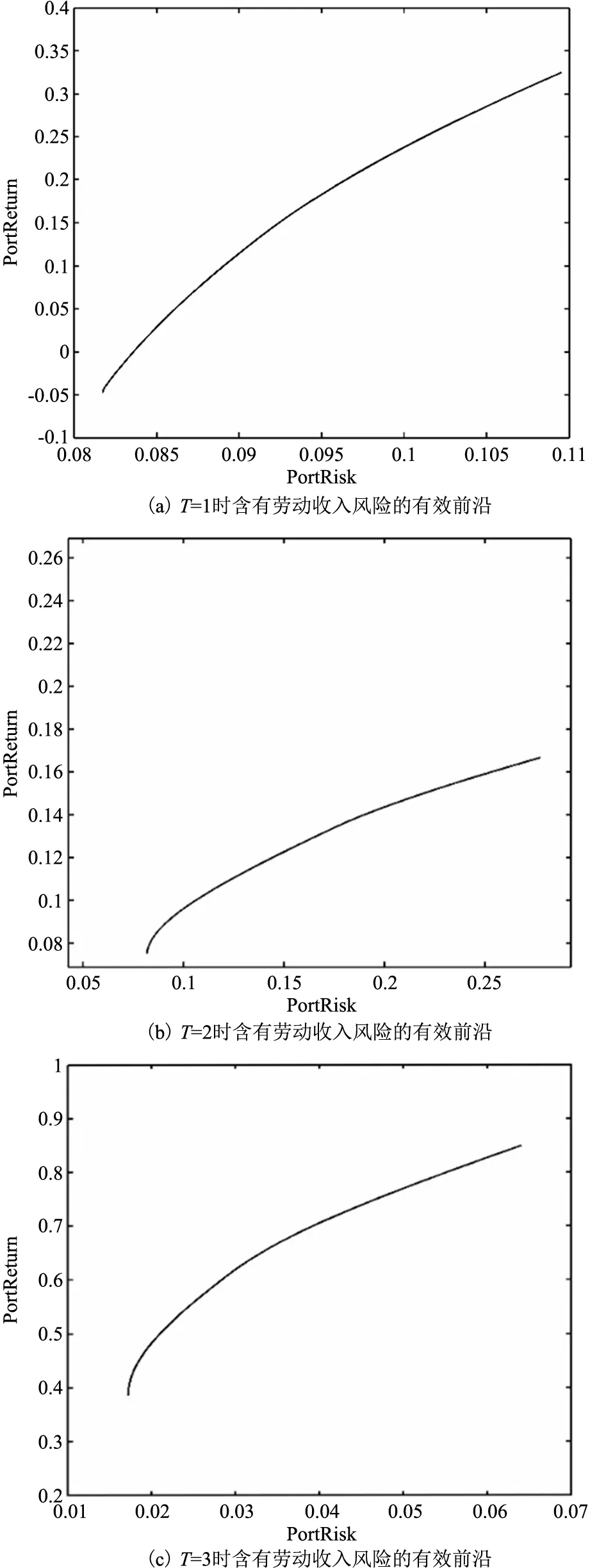
圖1 含有勞動收入風險的投資組合每一時期有效前沿

為了進一步說明勞動收入風險的引入對投資組合的影響，我們做出了多階段投資組合中考慮和不考慮勞動收入風險兩種情形下有效前沿對比圖2（a～c）。顯然，在相同的投資收益下，考慮勞動收入風險的投資組合有效前沿是在不考慮勞動收入風險投資組合的右邊。即當投資組合收益均值相同時，考慮勞動收入風險的投資風險要大于不考慮勞動收入風險的投資風險。因此，考慮勞動收入風險能夠更好的反映投資者所面臨的真實的投資環境，投資者如果忽視自身勞動收入風險，將會低估實際中所面臨的投資風險，從而引起投資損失。

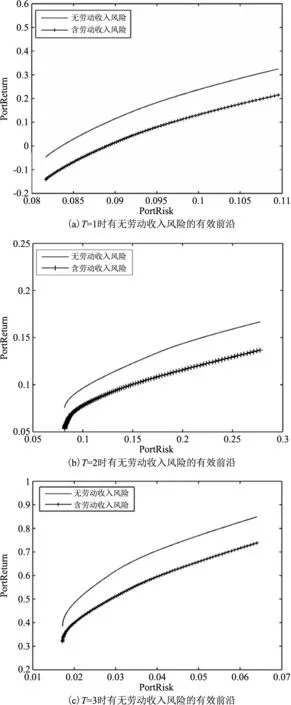
圖2 是否含有勞動收入風險的投資組合每一時期有效前沿

3.2 勞動收入風險的變動對多階段投資策略的影響

根據上文，我們發現在長期多階段投資中，勞動收入風險的引入會對投資組合的構建產生影響。那么勞動收入風險的變化具體會對資產選擇產生什么影響呢？

勞動收入風險的來源可以分為勞動收入本身的變化及勞動收入增長率與風險資產的相關關系。那么，勞動收入風險的變化可用勞動收入增長率方差以及其與風險資產的相關系數來衡量。因此，本節改變這兩組數據，研究勞動收入風險變化對多階段資產選擇的影響。設置勞動收入增長率的方差為0.0015、0.002和0.0025，勞動收入增長率與風險資產協方差為-0.006、0和0.006，得到投資者在長期多階段每一期不同勞動收入風險下的投資策略。

（1）本節給出了勞動收入增長率分別為0.04、0.1、0.2的情況下，勞動收入增長率的方差分別為0.0015、0.002和0.0025，且勞動收入增長率與風險資產相互獨立時，投資者在3個時期的投資策略（表略）。當勞動收入增長率與風險資產無關時，勞動收入增長率的方差越大，風險資產投資比例越小，無風險資產投資比例越大。圖3（a～c）是勞動收入增長率與風險資產無關時，無風險資產的投資比例隨著勞動收入增長率方差變動的變化圖，這3個圖更加直觀的表明無風險資產持有比例的變化趨勢。

（2）當勞動收入與風險資產正相關時，根據各資產的投資比例（表略），可畫出無風險資產的投資比例，如圖 4（a～c）。 從圖 4（a～c）可看出，當勞動收入與風險資產正相關時，隨著勞動收入增長率方差的增大，投資者會減少風險資產投資比例，增加對無風險資產的投資比例。

（3）圖5（a～c）展示了勞動收入風險與風險資產負相關時各個資產投資比例及其變化。可以清晰的看出，當勞動收入風險與風險資產負相關時，勞動收入增長率的方差越大，風險資產投資比例越高，無風險資產投資比例越低。

通過分析發現，勞動收入風險的變化會導致投資策略不同。考慮勞動收入風險的多期均值-方差模型更符合實際，投資者不僅要關注金融市場中的風險，更不能忽視自身勞動收入風險。

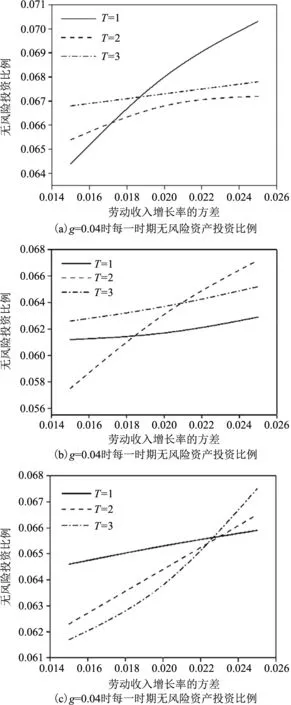
圖3 勞動收入與風險資產相互獨立時每一時期無風險投資比例

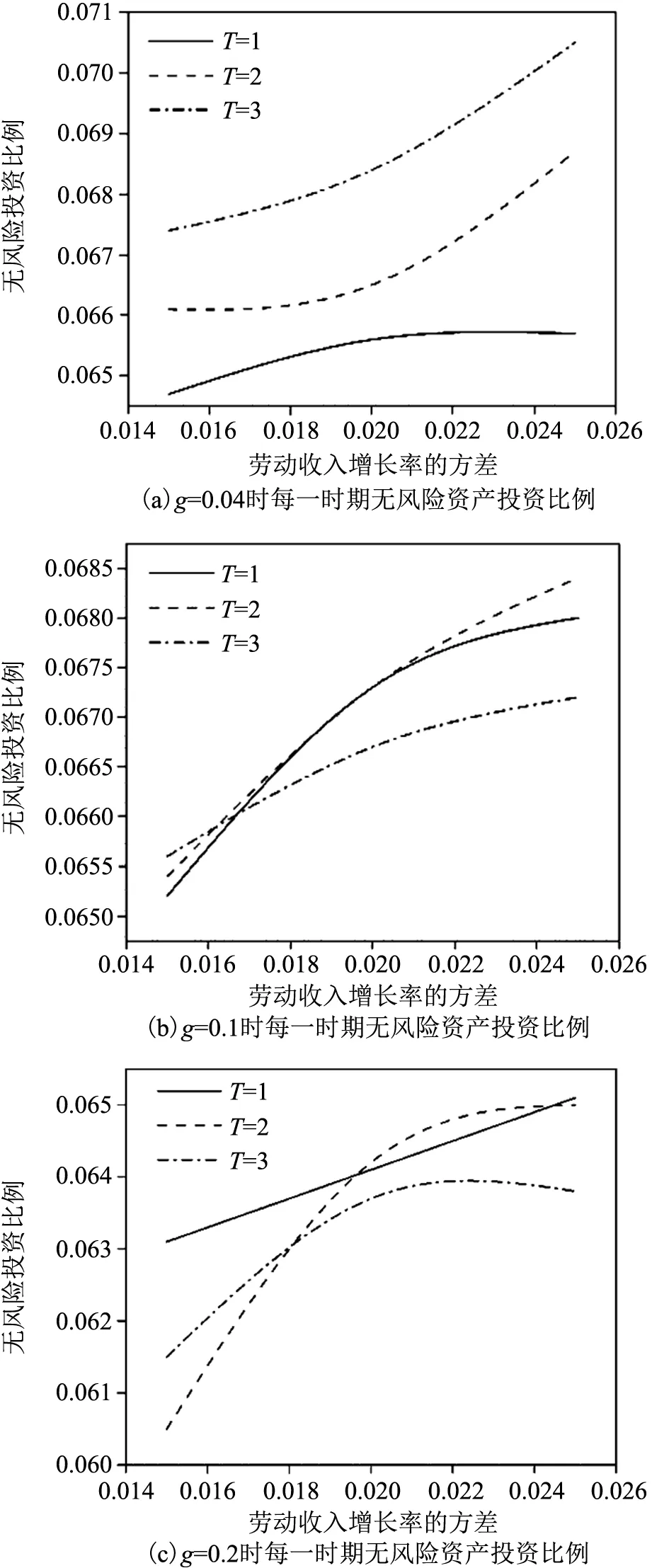
圖4 勞動收入與風險資產正相關時每一時期無風險投資比例

4 結 論

在實際金融市場中，投資者不僅需要處理金融資產自身產生的風險，同時也要化解勞動收入風險，使投資組合的風險得到合理的分散，獲得預期收益。本文考慮了具有勞動收入風險的多階段投資組合選擇問題，建立了考慮勞動收入風險的多期均值-方差模型，設計改進的遺傳算法求解該模型，使用MATLAB進行數值模擬，利用中國股票市場數據進行檢驗，驗證了模型的有效性，并進一步分析勞動收入風險的引入及變動對多期資產選擇的影響。結果表明，勞動收入風險的變動對多階段投資組合的構建具有復雜的影響。具體來說，在勞動收入與風險資產相互獨立及風險資產正相關的情況下，風險資產的投資比例與勞動收入風險的變化負相關，無風險資產的投資份額與其正相關。當勞動收入風險與風險資產負相關時，勞動收入風險的變大將導致投資者增加風險資產的持有比例，減少對風險資產的投資。因此，在多期投資中考慮勞動收入風險，可以更好地反映現實市場經濟環境，幫助投資者有效地選擇自己的投資組合。

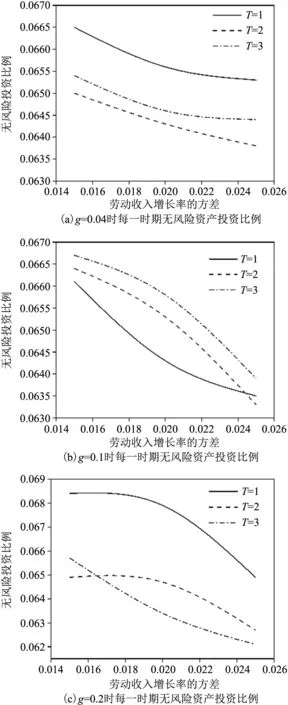
圖5 勞動收入與風險資產負相關時每一時期無風險投資比例