觀察聯(lián)想而有深度

唐秀農(nóng)

[摘? 要] 深度學(xué)習(xí)和深度教學(xué)理念的引進(jìn)促進(jìn)高中數(shù)學(xué)教學(xué)理念、內(nèi)容編排發(fā)生了變化，拓寬了學(xué)生的學(xué)習(xí)思維，豐富了教師的教學(xué)方法. 本文就深度學(xué)習(xí)和深度教學(xué)的內(nèi)容選用進(jìn)行分析，整合教學(xué)內(nèi)容，更新了數(shù)學(xué)教學(xué)理念.

[關(guān)鍵詞] 觀察;聯(lián)想;深度學(xué)習(xí);深度教學(xué)

筆者所在學(xué)校生源位居廣州市第三生源組. 學(xué)校學(xué)習(xí)風(fēng)氣較為濃厚，學(xué)生學(xué)習(xí)數(shù)學(xué)態(tài)度較為端正，但學(xué)生卻常因自己動(dòng)手解題沒有思路而倍感焦頭爛額，面對(duì)考試總感覺“我命由天不由我”. 經(jīng)調(diào)查了解，學(xué)生普遍反映：（1）公式、定理、公理能背誦默寫卻不知何時(shí)何處使用;（2）看完題目無法提取有效信息;（3）能接受課堂傳授知識(shí)卻對(duì)課后相應(yīng)練習(xí)束手無策. 筆者以為，學(xué)生存在的三個(gè)現(xiàn)象反映了學(xué)生在日常的學(xué)習(xí)中處于淺層學(xué)習(xí)狀，尚未能對(duì)課本知識(shí)、數(shù)學(xué)思想方法進(jìn)行深層次的理解與整合，未能真正意義上提高其數(shù)學(xué)核心素養(yǎng). 基于以上原因，近年來，筆者在高三復(fù)習(xí)教學(xué)中嘗試引導(dǎo)學(xué)生深度學(xué)習(xí)、進(jìn)行深度教學(xué)，通過引導(dǎo)學(xué)生觀察題目說聯(lián)想和感受，主抓基礎(chǔ)、提煉方法、重視思想的總結(jié)和提升，堅(jiān)持不懈，學(xué)生的數(shù)學(xué)成績(jī)和素養(yǎng)有了明顯的提升.

黎加厚教授在國(guó)內(nèi)首次介紹了深度學(xué)習(xí)的概念，提出深度學(xué)習(xí)是指在理解的基礎(chǔ)上，學(xué)習(xí)者能夠批判地學(xué)習(xí)新思想和事實(shí)，并將它們?nèi)谌朐械恼J(rèn)知結(jié)構(gòu)中，能夠在眾多思想間進(jìn)行聯(lián)系，并能夠?qū)⒁延械闹R(shí)遷移到新的情境中，做出決策和解決問題的學(xué)習(xí). 具體在數(shù)學(xué)教學(xué)中的指導(dǎo)作用，筆者以為是學(xué)生在了解數(shù)學(xué)的定義和概念前世今生、在理解它們的內(nèi)涵與外延基礎(chǔ)上，自主提出已認(rèn)知的數(shù)學(xué)知識(shí)、思想和方法，并將其和新知識(shí)內(nèi)容相結(jié)合，通過對(duì)紛繁的題干觀察分析、抽象聯(lián)想、具體應(yīng)用、回顧反思加深對(duì)知識(shí)的掌握.

習(xí)題是反映學(xué)生數(shù)學(xué)素養(yǎng)的鏡子、是提高數(shù)學(xué)素養(yǎng)的橋梁. 學(xué)生通過讀題、審題、聯(lián)想、類比、歸納、反思，明確解題的原則，體會(huì)到學(xué)習(xí)知識(shí)從淺層次認(rèn)識(shí)發(fā)端到深層次認(rèn)識(shí)收尾，充分感受數(shù)學(xué)知識(shí)、思想、方法、能力、應(yīng)用和技巧.

下面是“向量”一章小結(jié)復(fù)習(xí)時(shí)，由一道習(xí)題發(fā)散生成的習(xí)題課的教學(xué)實(shí)錄概況.

人教版A版數(shù)學(xué)必修4第119頁13題改編題：已知向量a，b滿足a=b=2，a·b=2，且（a-c）·（b-2c）=0，則b-c的最小值為________.

該題初看很平常，再看似乎有些難入手，但從不同角度觀察、審視、聯(lián)想、剖析、探究，發(fā)現(xiàn)它涉及了向量的模長(zhǎng)與數(shù)量積的運(yùn)算和幾何意義、點(diǎn)與圓的位置關(guān)系、直線與圓的位置關(guān)系、兩點(diǎn)間的距離、點(diǎn)到直線的距離、三角函數(shù)的基本關(guān)系、向量三角不等式等，還涉及劃歸與轉(zhuǎn)化、數(shù)學(xué)結(jié)合、函數(shù)等數(shù)學(xué)思想與方法，飽含豐富的知識(shí)點(diǎn)，具有積極的訓(xùn)練意義. 然而在實(shí)際教學(xué)中有些教師不屑一顧，往往就題講題，忽視了其內(nèi)在信息和引導(dǎo)作用，殊為可惜. 下面僅以此題為例，談?wù)勅绾我龑?dǎo)學(xué)生進(jìn)行深入學(xué)習(xí)，以期同仁不吝指正.

對(duì)題目的外在淺層認(rèn)識(shí)

認(rèn)識(shí)1：見到a=b=2，a·b=2，給人的感覺是向量a，b的長(zhǎng)度以及它們的夾角是確定不共線的，由平面向量基本定理自然想到可以將向量a，b表示向量c，那么問題就迎刃而解了.

認(rèn)識(shí)2：見到已知（a-c）·（b-2c）=0，不難聯(lián)想到向量數(shù)量積為零，意味著兩向量互相垂直，而向量a，b的長(zhǎng)度和夾角已經(jīng)確定. 為確定向量c的位置，很快就有了對(duì)已知條件的變形（c-a）·c-■b=0，從而確定向量c的終點(diǎn)的軌跡是以向量a和■b終點(diǎn)所在線段為直徑的圓.

認(rèn)識(shí)3（深層）：從所求問題出發(fā)直接把求模的問題轉(zhuǎn)化為求數(shù)量積也是一種常見的思路. 由（a-c）·（b-2c）=0得c2=■b·c+a·c-1，將其代入b-c2=b2-2b·c+c2，化簡(jiǎn)得b-c2=3-■b·c+a·c. 該式子中的變量既有模長(zhǎng)，又有夾角，計(jì)算難度會(huì)增大，往下計(jì)算會(huì)導(dǎo)致學(xué)生半途而廢或算錯(cuò). 重新審視題目的條件和所求的問題，從整體上把握該式，聯(lián)想到向量中的三角不等式，結(jié)合已知條件，構(gòu)造一個(gè)能與條件（a-c）·（b-2c）=0有關(guān)且又能消掉向量c的式子，問題便可得解.

由所求的問題出發(fā)，通過“外在認(rèn)識(shí)”將已知條件進(jìn)行適當(dāng)變形，尋找其幾何意義，由淺到深，為即將實(shí)施的解題過程提供了夯實(shí)的條件儲(chǔ)備——萬事俱備，只欠東風(fēng).

對(duì)題目的教學(xué)分析和引導(dǎo)

教學(xué)分析引導(dǎo)1：有了認(rèn)識(shí)1就知道思路之一是將向量a，b表示向量c，若是令c=xa+yb，會(huì)增加向量數(shù)量積的運(yùn)算，自然而然地引導(dǎo)學(xué)生建立坐標(biāo)系解決問題. 而在建系寫點(diǎn)的坐標(biāo)過程中，問題“求b-c的最小值”可聯(lián)想到令向量b的縱坐標(biāo)比令向量a為0更加容易運(yùn)算，充分體現(xiàn)了“目標(biāo)導(dǎo)航”的作用，減輕了計(jì)算量，體現(xiàn)了解題的技巧.

解法1：借助“認(rèn)識(shí)1”中得到的思路，不難得到a=（1，■），b=（2，0）. 設(shè)c=（x，y），代入（a-c）·（b-2c）=0，化簡(jiǎn)得（x-1）2+y-■■=■■，即向量c的終點(diǎn)的軌跡是以1，■為圓心，■為半徑的圓. b-c=■的幾何意義為點(diǎn)（2，0）到圓上的點(diǎn)的距離，其最小值為圓心到點(diǎn)（2，0）的距離減去半徑，即■.

“坐標(biāo)法”是解與平面向量基本定理有關(guān)問題的一個(gè)通法，有助于減少運(yùn)算量.

解法2：同解法1，b-c=■的幾何意義是以點(diǎn)（2，0）為圓心的圓的半徑長(zhǎng). 當(dāng)兩圓外切時(shí)，半徑長(zhǎng)最短，即圓心距離減去半徑：■-■=■.

以上兩種解法均為“坐標(biāo)法”，此法把向量問題轉(zhuǎn)化為解析幾何問題，既能復(fù)習(xí)向量的知識(shí)和方法，同時(shí)又回顧了有關(guān)圓的知識(shí)，實(shí)現(xiàn)了一箭雙雕，是解決向量問題的一種通法.

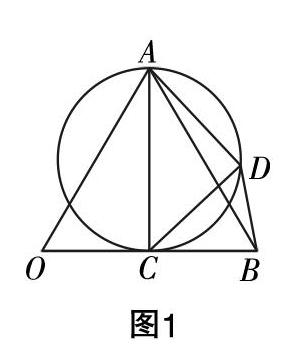
教學(xué)分析引導(dǎo)2：由（a-c）·（b-2c）=0可化簡(jiǎn)為（c-a）·c-■b=0，向量c的終點(diǎn)的軌跡是以向量a和■b的終點(diǎn)所在線段為直徑的圓.

解法3：如圖1所示，易得∠AOB=■，BC=1，■=■b，AC⊥OB，不妨設(shè)∠CAD=θ，則∠BCD=θ，CD=ACsinθ=■sinθ. 在△BCD中，由余弦定理得BD2=BC2+CD2-2BC·CDcosθ=1+3sin2θ-2■sinθcosθ=■-■sin（2θ+φ）tanφ=■，故BD2≥■=■=■■，當(dāng)且僅當(dāng)sin（2θ+φ）=1時(shí)，取到等號(hào). 故其最小值為■.