尋根悟法 積石成山
——談高中數學試題的“命、解、評”

黃 健 (江蘇省蘇州市教育科學研究院 215000)

提升解題能力和命題能力是教師專業發展的必由之路，這是課堂教學、理論研究中不可或缺的基本功，也是其專業功底、教學素養和教學水平的綜合體現．我市教科院已連續多年組織了教師學科素養大賽和試題“命、解、評”團隊比賽．從實踐情況看，大部分教師對試題的理解不到位，只看局部而忽視整體，不注重問題間的聯系，無法把握核心本質．也有一部分教師的理念與時代脫節，缺乏研究意識，對新課標的育人理念不重視，對試題的發展方向不了解，教學方向發生偏差．只有明確方向、把握規律、認清本質，一線教師才能做到思想浸潤、方法自覺，從而大幅提升專業認知能力．下面筆者結合實踐，談談對高中數學試題命、解、評的研究，希望對廣大教師有所啟發．

1 解題過程是對數學知識的認識與領悟

數學問題通常分為兩類：推理類和化歸類．解推理類問題，就是運用公理、定理、公式等手段將問題逐步簡化并最終達成目標．解化歸類問題，就是將未知的數學問題轉化為已經解決的問題．

每一個數學問題都有一條或多條解決途徑，解題一般都是從現有知識或經驗出發．知識與經驗是區分解題能力強弱的重要因素，教師要努力提升自身的解題經驗，并通過闡述解題的心路歷程及體會，激發學生的探究熱情，豐富認知，提升解題能力．解題經驗的提升，一要加強學習與培訓，二要培養探索與反思的習慣，通過研究方法的科學性、合理性，總結提煉問題本質，來加深對問題的理解．我們建議做到以下幾點．

1.1 關注差異與方向

首先，從宏觀視野下觀察已知條件和目標的差異．比如，已知什么，目標是什么？如何在已知與目標間搭建橋梁？其次，從微觀層面上觀察問題的結構特征．比如，已知與目標間的代數差異有哪些？

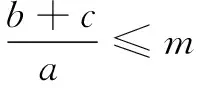
分析 本題已知角度關系，目標是研究邊的數量關系，因此消除邊角差異是解題的突破點．

圖1

1.2 挖掘問題本質

數學問題的本質是數量結構和存在關系的內在聯系，探求問題本質的過程是驗證結構和關系方法的過程．其中挖掘數式整體特征和圖形特征是重要手段，教學中要了解常見數式特征與幾何圖形的關聯，熟悉數與形各自的解題優勢，重視兩者的相互轉化．

例2已知m，n∈(0,+∞)，且m+3n=1，則mem+3ne3n的最小值是．

分析 先從宏觀角度觀察，令x=m，y=3n，問題轉化為：已知x>0，y>0且x+y=1，求xex+yey的最小值．代入消元是最容易想到的方法，但消元時，若不注意“消去的元”對“保留的元”有范圍的約束，則容易產生錯誤．那么，本題的本質是什么？

點評 本題的代數本質是排序不等式．

圖2

圖3

1.3 形成思維模型

新課標指出，高中數學教學要以發展學生數學學科核心素養為導向，創設合適的教學情境，啟發學生思考，引導學生把握數學內容的本質．形成思維模型是學生實踐能力發展的一個關鍵節點．簡單地講，思維模型就是思想的基本過程，也是思維的結構與習慣．通過思維模型可以快速找到解題方向，突破難點．加強解題的一般性研究，最終形成思維模型，是提升解題能力的重要方法，教學中應從具體問題中去挖掘．比如，常見局部條件的思維出發點在哪里？解決某類問題的一般路徑有哪些？局部常見手段有哪些？而思維導圖是思維模型的形象呈現，如圖4是平面向量數量積問題的思維模型導圖．

圖4

2 講評過程是對數學思想的總結與反思

教師充分研究問題后，需要將研究成果分享給學生，這個過程包括講題與評題．講題是要將問題的基本思想與解法呈現給學生，而評題是點評試題考查方向、滲透本質屬性、探尋一般特征、激活發散思維的重要手段．兩者前后關聯、相輔相成，它們能優化學生認知結構、提高思維素質，激發創新能力．講評效果的好壞取決于教師對問題理解、把握的深刻性，以及課堂的藝術性．建議做到以下幾點．

2.1 注意講評的層次性

高中三年中，由于學生在不同時期認知的水平不同，教師對某類問題講解與滲透的策略應是不同的．講評的深度原則上要符合學生當前的思維水平．因此，教師要加強對教材、課標等的整體理解，把握好學生不同階段的思維層次，做好“三年一盤棋”的規劃．

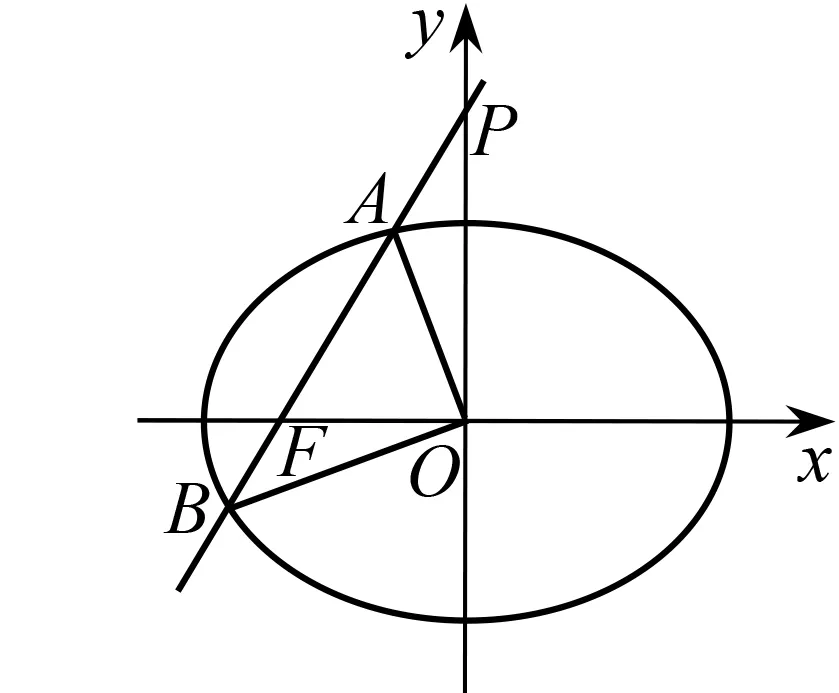
圖5

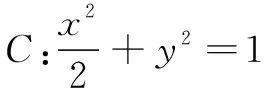
分析 學生對解析幾何問題的理解往往會經歷四個階段：簡單認知、邏輯認知、特點認知、核心認知．

簡單認知直接求解

邏輯認知分析相關點聯系

特點認知抓二次曲線結構特征

核心認知追根溯源探尋本質

2.2 善于挖掘共性問題

高效的課堂需要師生間的交流，優秀的教師上講評課絕不是照本宣科，他們善于挖掘學生解題過程中的共性問題，通過展示一般解法，分享學生妙法，對比解法優劣，指出典型錯誤，分析交流錯因(知識上、邏輯上、心理上、策略上和評分點上)，引導學生總結等手段，同時將講評落到實處．

圖6

分析 本題是一道統考題，對運算要求較高，從實際檢測情況看，能夠完全做對的學生鳳毛麟角，部分學生可以猜出答案，但說理過程混亂．大部分學生的解答過程如下：

不難發現，本題暴露的共性問題是學生計算能力偏弱，對字母運算心存恐懼，解題手段單一，難以突破運算關．對此，教師應作如下引導：優化運算的途徑有哪些？題干中的關鍵詞有哪幾個？定點定值問題的解題策略是什么？從學生解題的卡點開始，進行交流與展示．

2.3 重視局部細節展示

講評課切忌從頭到尾不分重點，一講到底．教師應深入備課、深入研究，以點帶面，突出重點、攻破難點．尤其要重視局部細節的過程展示，通過探索、迂回、構建、發散等方式開展交流，必要時還可設置問題微專題進行延伸拓展，引導學生整理、反思、總結、提煉．題目背后的東西要講清、講透，如：考查了哪些知識點？應用了什么方法？核心點在哪里？必要時可設置一組或幾組類似題來強化訓練，真正幫助學生將問題解決．

下面就例5談談如何進行局部細節的展示，解題的關鍵點應從恒等式出發．

(帶著學生逐步演算，注重整體特征研究，能有效提高運算能力)

(抓住關鍵詞“恒成立”，從特殊值下手先找后證，有效突破)

方法3 首先當A(-2，0)，B(2，0)時，猜想得M(1，0)．其次設y=k(x-1)，利用韋達定理代入證明即可．

(方法3和方法4是對特殊值法的深入優化)

3 命題過程是對研究成果的展示與深化

經過多年的積累，教師經歷了從解題到評題的全過程后，可以開始嘗試參與各類命題活動和命題比賽．命題是教師追求專業進一步發展的必由之路，命題能力反映了教師的研究水平．命題過程也是教師對自身研究成果的展示與深化，教師一方面可以在命制題目上展示自身的研究方向和教學主張，另一方面，在與同伴的磨題過程中會產生很多新想法，發現很多新結論，教師的認知水平又能得到進一步提高．

命題的境界大致可以分為兩層：第一層是組合模仿，就是將陳題進行深化、改造、類比，常見的有改頭換面、換元轉換、調換邏輯、模型重組等形式；第二層是突破創新，這基于教師對某一領域有突破性的研究，要求具備較豐富的想法和較強的探索能力．從事命題研要注意以下幾點．

3.1 強調語言的嚴謹性與科學性

命題的首要前提是要保證題目不能犯科學性錯誤，不僅要結果準確，而且還不允許存在歧義．試題中的關鍵詞都要反復斟酌，防止出現因表達不嚴謹而導致的學生理解上的偏差，另外試題語言要符合學生的閱讀習慣，盡可能少用長句或雙重否定句，要體現親和性．

例6在等比數列{an}中，已知a2=2，a6=8，則a2與a6的等比中項為．

分析 此類問題的爭議之處為“a2與a6的等比中項為”.學生做填空題的時候，思維在一定程度上是開放的，有部分學生會問：“答案難道不能為a4嗎？”從而暴露出設問的不嚴謹，可以修改為“a2與a6等比中項的值為．”

例7已知圓O：x2+y2=1，點A，B在動直線l：ax+y-4a=0上，且AB=2．若圓O上存在點C，使得△ABC為等腰直角三角形(C為直角頂點)，則實數a的取值范圍為．

分析 本題對A，B兩點的理解頗有爭議，直線l繞著定點(4，0)轉動過程中，點A，B相對于點(4，0)是否在動？為了強調A，B是動點，可修改為“若直線l：ax+y-4a=0上存在相距為2的兩個動點A，B，圓O：x2+y2=1上存在點C，使得△ABC為等腰直角三角形(C為直角頂點)，則實數a的取值范圍為．”

例8已知f(x)是二次函數，f(0)=f(5)= 0，f(-1)=12，求f(x)在[0，m]上的最小值．

分析 本題的最小值是常數還是含有m的式子？事實上，只要修改為“求f(x)在[0，m]上的最小值g(m)”就能消除歧義．另外還可增加設問，鞏固學生對問題的理解，如：“當m變化時，求g(m)的最小值．”

3.2 注意對教材問題的再加工

教材是課標理念的集中體現，基于教材模型可以編擬出很多經典問題．教材改編題背景公平，體現基礎性和導向性，重點突出，難度適中，它能讓教師更準確地把握方向．對這些教材改編的經典問題，教師要學會多角度思考與研究，掌握解題的源與流，從而激活靈感，激發新的命題動力．

基于此想法，如果條件適當改變，可用類似方法解決．

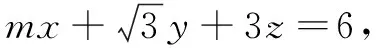
上述問題的解題靈感從何而來？其實是源于一道課本經典題：“利用函數的單調性，證明不等式ex>x+1，x≠0，并通過圖象直觀驗證．”此題的幾何本質是函數y=ex與其在(0，1)處切線的位置關系，它給命題者提供了切線放縮的思路．此外，通過換元等方法對問題改造，可衍生出一系列重要結論．由于篇幅原因，本文不再贅述.

3.3 重視試題的實際背景和育人價值

命題的創新力源于生活，好的原創題都有較為深刻的實際背景和育人價值.新課標要求學生用數學眼光觀察世界，用數學的思維分析世界，增強創新意識和探究精神，因此教師要努力挖掘生活中的素材，引導學生養成開放探究的習慣，增強實戰能力．

圖7

例10如圖7，某種螺帽是由一個半徑為2的半球體挖去一個正三棱錐構成的幾何體，該正三棱錐的底面三角形內接于半球底面大圓，頂點在半球面上，則被挖去的正三棱錐體積為．

分析 本題以螺帽為載體，研究幾何體的體積，涉及對運算能力和數據處理能力的考查，呈現了數學之美，讓學生感受數學的應用價值．

(1){Sn}中是否存在連續三項成等差數列，若存在，請證明；若不存在，說明理由．

(2){Sn}中是否存在連續四項成等差數列，若存在，請證明；若不存在，說明理由．

分析 探究性問題是新高考的熱點之一，本題以函數為載體給出遞推關系，逐層遞進，引導學生分析探究，促進其對數學本質的理解，有效提升了學科素養．

4 結語

王尚志教授指出，應培養好中國學生在數學學習中的六大核心素養，具體到教學層面來說，教師要運用分析、對比、聯想等手段來引導學生觀察、計算、推理、化簡、化歸和反思，提升其發現問題、提出問題、分析問題、解決問題的能力．命題、解題、評題是高中數學教學永恒的話題，三者相互關聯，相互促進，脫離了習題教學，高中數學教學就如一潭死水，毫無生氣．建議廣大教師加強對試題方向性、本質性和一般性的研究，通過數形結合、轉化化歸等手段，探求研題思路、反思研題過程，真正領悟問題核心，使解題能力變得游刃有余．同時要科學引導，教會學生“怎樣思考”、“怎樣自然地想到”，運用探究等方式激活思維，使學生經歷知識發生、發展和形成的深度學習過程，運用聯想、遷移等教學手段幫助學生建構認知體系，學會融會貫通，達成發展思維、提升課堂效率的目的，引領學生成為真正的數學高手！