數學文化視角下微專題設計與教學
——以“橢圓及其輔圓”教學為例

劉國祥 (江蘇省宜興中學 214200)

數學“微專題”設計是圍繞教學關鍵點和疑難點、對具有緊密相關的知識或方法進行的整體設計．微專題教學具有“見微知著”的特點，能夠幫助學生架構完整的知識結構、方法結構，促進學生主動參與，撬動深度學習．我校高三數學備課組在二輪復習中一直嘗試穿插以“一題一課”為背景的微專題教學，效果顯著．所謂以“一題一課”為背景的微專題設計，就是在一節課的教學設計中選擇一個典型問題，通過對典型問題進行教材尋根、解法探究、變式拓展、鏈接應用環節的教學，梳理知識結構，建構方法體系，促進學生積極主動地學習，提升學生的核心素養．

《普通高中數學課程標準(2017年版)》指出：數學文化是指“數學的思想、精神、語言、方法、觀點，以及它們的形成與發展；還包括數學在人類生活、科學技術、社會發展中的貢獻與意義，以及與數學相關的人文活動”．《關于2018年普通高中考試大綱修訂內容的通知》中增加了數學文化的考查要求.在高考試題中滲透數學文化，能正確引導中學數學教學關注數學文化，將數學本質教授給學生．如何在高三微專題的設計與教學中滲透數學文化，提升學生的核心素養，是值得關注的話題．本文以“橢圓及其輔圓”微專題教學為例來說明數學文化視角下的微專題設計與教學．

1 問題呈現

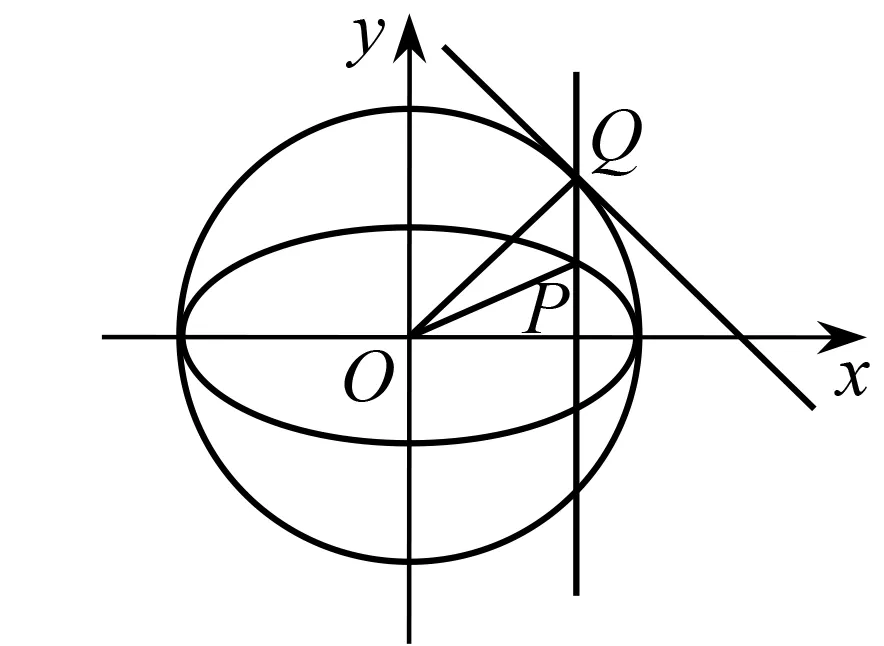
圖1

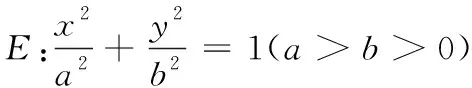
問題解讀 本題為引入新定義的題型，給出橢圓輔圓的定義及性質，以直線與圓、直線與圓錐曲線關系為考查背景，重點考查學生的閱讀理解能力、數學建模能力以及邏輯推理能力，讓學生經歷從特殊到一般的數學問題探索過程，問題解決體現了數學的理性精神．

學情分析 學生解答本題的困惑：對橢圓的輔圓定義理解表層化；對橢圓及圓生成過程的邏輯關系理解不到位；對三角形面積建模不合理；不會用從特殊到一般的思路來探究直線與橢圓的位置關系并給出證明．

價值分析 本題的背景是數學名題——用尺規法作橢圓切線．利用“典型題”設計課堂教學，不僅可以讓學生體會到數學思想方法在解題中的地位和作用，而且可以讓他們體會到數學知識是立體的、相互聯系的，體現數學文化的無窮魅力，促進學生思維的發展及智慧的涵養．

2 教學設計

2.1 教材尋根，滲透史料

數學教材隱含著豐富的史料，將散落在教材各處的史料整合重組成課程資源， 讓學生了解概念的形成背景和歷史條件，建構研究一類問題的思想方法，同時還具有豐富的育人價值．

問題鋪墊1(蘇教版選修2-1第31頁例2)：將圓x2+y2=4上的點的橫坐標保持不變，縱坐標變為原來的一半，求所得曲線的方程．

問題鋪墊2(蘇教版選修2-1第38頁探究拓展15) ：橢圓可以視為對圓上的點向同一條直徑施行伸縮變換而成，應用橢圓和圓之間這種關系，你能依據圓的面積公式來猜想橢圓的面積公式嗎？

問題鋪墊3(蘇教版2-1第38頁第12題)：已知圓柱的底面半徑為4，與圓柱成30°角的平面截這個圓柱得到橢圓，求橢圓的離心率．

2.2 解法探究，滲透思想

師：正確理解輔圓定義是解答第(1)問的關鍵，依據定義探究橢圓方程．

師：正確理解輔圓性質是解答第(2)問的關鍵，設橢圓上任意一點P(x0,y0)，則點P的上輔點Q的坐標是什么？如何證明？

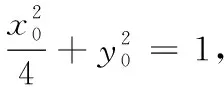
評析數學語言是數學文化的重要組成部分，正確理解數學語言是學習數學文化的重要途徑，我們需要培養學生閱讀文本、提煉數學模型的能力．在閱讀中首先關注特殊情況，然后推廣到一般情況，理解題意并找出問題的根源取決于推理能力的強弱．

師：依據本題條件如何合理表征△OPQ的面積？

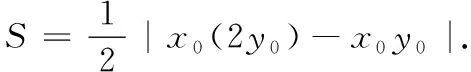
評析處理面積問題的關鍵是依據問題特點建立適當的模型.三角形面積表示方法體現了多樣性和靈活性，課堂上要放手讓學生去探究，引導學生從多角度思考問題，然后依據問題特點選擇最優方案．

師：本題是一個開放題，結論如何尋求？

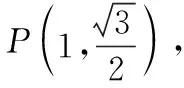
師：請設計證明結論路線圖.

生5：設點Q(x0,y0)→切線QT方程→求出T的坐標→直線PT的方程→利用判別式Δ證明PT與橢圓相切．

評析本題呈現開放性試題的命題思路，不在題目中限定結論，給學生留下思考、分析、判斷的空間；通過特殊化猜想結論，通過邏輯推理來驗證猜想，體現了研究性學習理念，考查考生的理性思維．同時通過探究，構建了證明切線的兩種思路，促進了方法體系的構建．

2.3 拓展推廣，滲透數學美

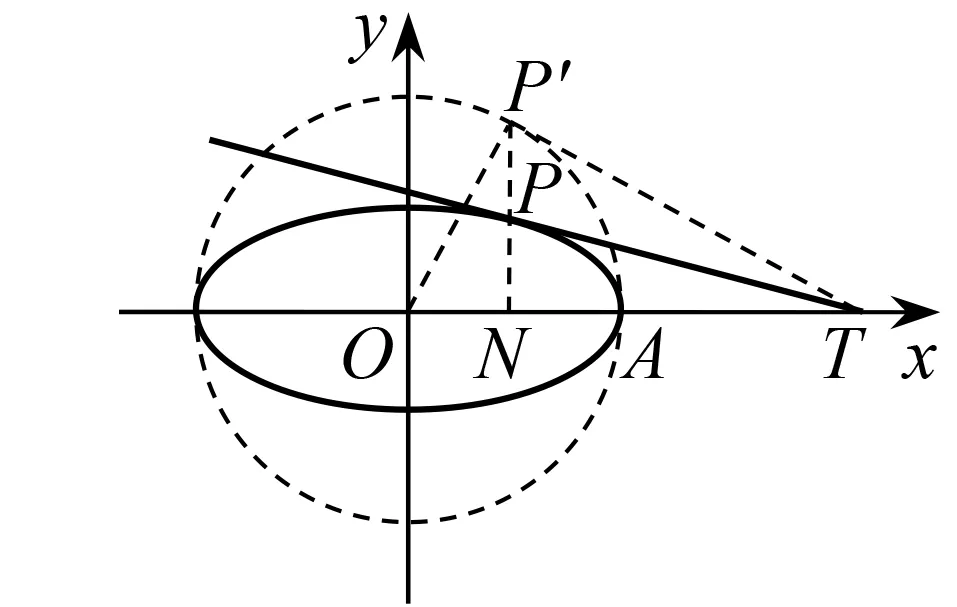
圖2

評析本題的命題背景為過橢圓上一點處切線作法的合理解釋.將問題從具體事例推廣到一般情況，展示了數學方法的生成過程，使數學教學過程成為發現、創造數學的過程，讓學生學會欣賞數學的簡潔美．學生不禁會提出問題：如何過橢圓外一點作橢圓的切線？

性質2從焦點F1作橢圓在點P處的切線的垂線，垂足為點A，則點A在輔助圓上．

背景史料：閱讀蘇教版2-1第58頁“圓錐曲線的光學性質”，體會圓錐曲線光學性質在生活中的廣泛應用．

探究1 設F1,F2分別是橢圓的兩個焦點，P是橢圓上任意一點，則從F1出發的光線經過橢圓在P處的切線l反射后的反射光線經過點F2嗎？

生6：作點F2關于l的對稱點F2′，只要用反證法證明F1,F2′,P三點共線．

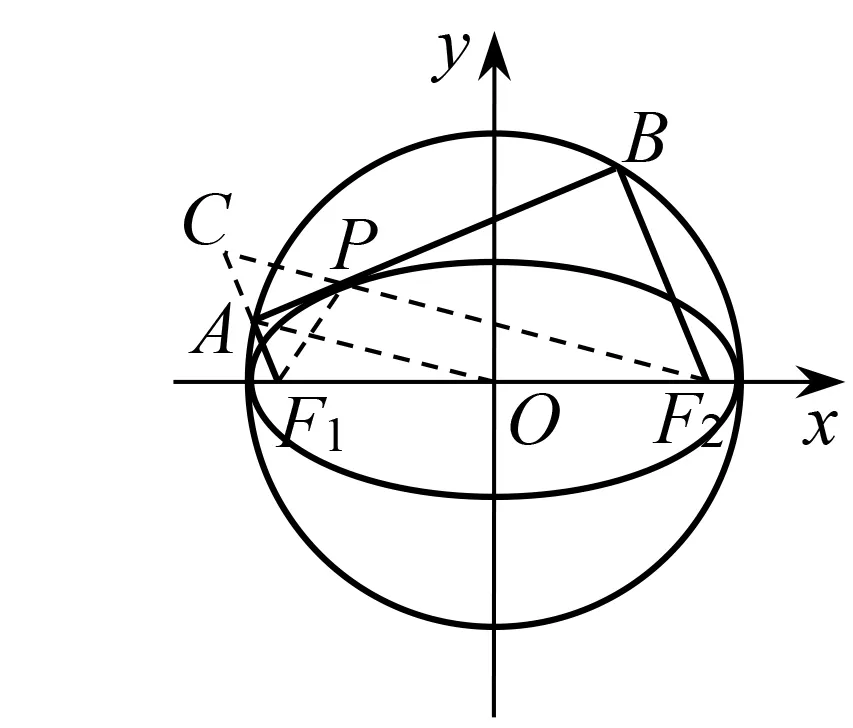
圖3

探究2 從焦點F1作橢圓在點P的切線的垂線，垂足為點A， 則點A在輔助圓上．

生6：作F1關于切線的對稱點C(圖3)，因為BA為橢圓切線，所以C,P,F2共線，CF2=CP+PF2=PF1+PF2=2a，則OA=a．

同樣，利用該結論可以過橢圓外一點P作橢圓的切線，即以PF1為直徑的圓與輔助圓交于點E,D，則PE,PD為橢圓的切線．

評析從教材閱讀材料中提煉出數學結論，讓學生體會數學結論在實際生活中的運用；同時培養學生以理性觀點看待結論，探究問題背后的原因，用平面幾何知識和反證法不難證明．利用性質2解決用尺規法過橢圓外一點作切線的問題．這樣的過程能引導學生用數學眼光看待世界、用數學思維分析世界，打造數學和生活的聯系，使數學知識得到活化．

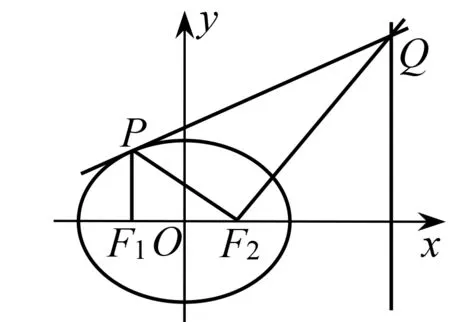
圖4

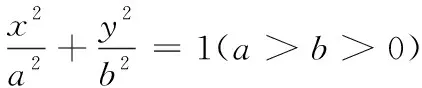
評析變式拓展題從另外一個角度作橢圓切線，可以看做應用結論解決問題．

2.4 鏈接高考，滲透應用

前面給出了用尺規法作橢圓上一點處的切線和過橢圓外一點作橢圓切線的原理，其他圓錐曲線是否有與本題類似的結論？這一問題引發了學生的拓展性思考．

鏈接高考(2016年全國Ⅰ卷第20題)：如圖5，在直角坐標系xOy中，直線l：y=t(t≠0)交y軸于點M，交拋物線C：y2=2px(p>0)于點P，M關于點P的對稱點為N，連結ON并延長交拋物線C于點H．

評析本題從拋物線外一點通過尺規作圖的方法作拋物線的切線，這一過程緊貼學生的最近發展區，容易激發學生探究知識的好奇心．教學生學會學習的關鍵是對學生的學習進行方法引領，只有學生覺得方法是有用的，才能引發出情感共鳴，進而提升核心素養．

3 教學啟示

3.1 滲透史料，設置問題鋪墊，優化知識結構

數學史料呈現了古今中外知識發展演變的真實過程，追溯問題的來龍去脈，體悟問題解決的曲折艱辛，蘊含了重要的育人價值．在微專題設計中要從學生的認知基礎出發，分析學生的知識薄弱點、思維障礙點，把優化知識結構作為設置問題鋪墊的起點.教材有豐富的數學史料，是高考命題的依據，可對教材的例題、習題、復習題、探究與發現、閱讀材料中蘊涵的史料進行全面梳理，重新組合設計成針對性強的問題鋪墊， 建構完整知識結構．如本題通過三個問題鋪墊呈現橢圓與圓之間統一性的三個史料，橢圓性質可以通過類比圓的發現和推證，建構起解決橢圓與圓問題清晰的“路線圖”．

3.2 滲透思想，設置問題探究，提升高階思維能力

著名數學家柯朗指出：“數學思想，作為人類思維表達，反映了人們對縝密周詳的推理以及對完美境界的追求．它的基本元素是：邏輯與直觀、分析與構作、一般性和個別性，正是這些相互對立的力量的相互作用，構成了數學科學的生命、用途和崇高價值．”微專題教學不僅要重視知識、技能，更要領悟數學的思想，經歷數學的思維分析過程，以數學思想為魂統領復習，提高高階思維能力．本