位似：初中數學教師值得研究圖形變換*

潘金城 蔡雪梅 (江蘇省揚中市外國語中學 212200)

近幾年中等教育類(數學)期刊上刊發了不少以位似為主題的研究文章[1-2]，以位似為背景的試題也在不斷創新，這充分說明位似作為特殊的相似越來越受到數學研究人員的重視．本文就位似的深度運用及其價值進行例析，以饗讀者．

1 “位似”定義的核心條件與性質

文[1]指出，位似定義的核心條件是：(1)對應點的連線交于一點；(2)對應點到定點的距離之比等于常數，兩個條件缺一不可．特別地，平移前后的兩個圖形、半徑不等的兩個圓也是成位似的．

文[3]指出，位似變換是特殊的相似變換，因此位似圖形具有相似圖形的一切性質．包括： (1)兩個位似圖形的對應角相等，對應邊成比例；(2)兩個位似圖形的對應線段之比等于位似比；(3)兩個位似圖形的面積之比等于位似比的平方；(4)兩個位似圖形的對應線段平行(或在同一條直線上)且相等．

文[4]指出，位似變換具有傳遞性：若圖形A與圖形B成位似，圖形B又與圖形C成位似，則圖形A與圖形C成位似．

文[5]還指出，兩個不同的二次函數圖象成位似．此結論雖然在此文中已經證明，但方法比較繁瑣，本文運用文[1]中位似定義的核心條件給出如下簡潔的證明：

由于所有的二次函數的圖象通過平移、旋轉都能轉化為y=ax2的形式．根據位似的定義與性質可知，只要證明二次函數y=a1x2與y=a2x2的圖象成位似，即證明了兩個不同的二次函數圖象成位似．

圖1

2 關于“位似”性質的深度運用

在《義務教育教科書(數學)》中，“位似”的運用僅局限于“以已知點為位似中心，把一個圖形按給定相似比進行放大或縮小”和“會判斷簡單的兩個圖形是否成位似”．但作為數學教師要擇高處立、向寬處行，掌握“位似變換”的深度運用，促進優秀學生高階思維的深層次發展．

例1如圖2，在△ABC的AB,BC邊上若存在點M,N，使得AM=MN=NC，請作出符合條件的點M,N．

分析 (1)特殊化．若AB=BC，作∠ACB的平分線CM交AB于點M，過點M分別作BC,AC的平行線交AC,BC于點P,N(圖3)，易證MN=CN=AM．

圖2 圖3

圖4

(2)一般化．若AB≠BC，此時可轉化為BD=AB的特殊化情形.但點C′在AC上，易作菱形P′C′N′M′，其中點P′在AD上且P′M′∥BC(圖4)．

(3)目標化．解決問題的關鍵就是將M′,N′放縮后的對應點M,N分別落在AB,BC上，位似是問題解決的重要工具．

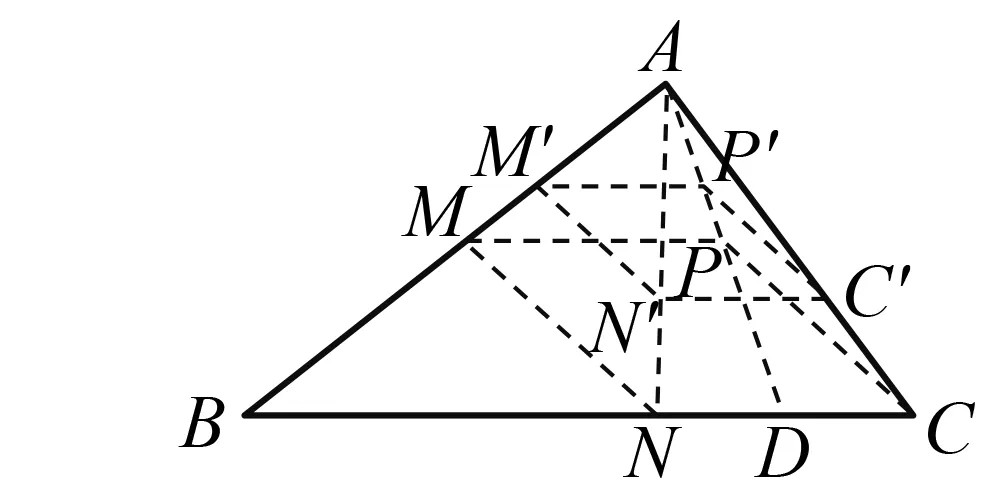
圖5

作法(1)在BC上取點D，使得BD=AB；

(2)作菱形P′C′N′M′，其中點P′在AD上且P′M′∥BC；

(3)連結AN′并延長交BC于點N，過點N作M′N′的平行線交AB于點M(圖5)．

圖6

例2(2018鎮江市中考題)如圖6，二次函數y=x2-3x的圖象經過O(0,0),A(4,4),B(3,0)三點，以點O為位似中心，在y軸的右側把△OAB按相似比為2∶1放大，得到△OA′B′，二次函數y=ax2+bx+c(a≠0)的圖象經過O,A′,B′三點．

(1)畫出△OA′B′，并求二次函數y=ax2+bx+c(a≠0)的表達式．

(2)點P(m,n)在二次函數y=x2-3x的圖象上，m≠0，直線OP與二次函數y=ax2+bx+c(a≠0)的圖象交于點Q(異于點O)．

①求點Q的坐標(橫、縱坐標均用含m的代數式表示)；

②連結AP，若2AP>OQ，求m的取值范圍；

③當點Q在第一象限時，過點Q作QQ′平行于x軸，與二次函數y=ax2+bx+c(a≠0)的圖象交于另一點Q′，與二次函數y=x2-3x的圖象交于點M,N(M在N的左側)，直線OQ′與二次函數y=x2-3x的圖象交于點P′．若△Q′P′M∽△QB′N，求線段NQ的長度．

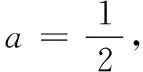
(2)解決問題(2)中的③的難點，要理解點P′為OQ′的中點，借助位似就不難知道△QB′N與△Q′P′M的相似比為2，從而將問題轉化為：當NQ=2Q′M時，求NQ的長度．

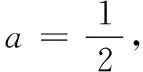
(2)①由位似性質知，位似比為2，故點Q的坐標為(2m,2n)．因為n=m2-3m，所以Q的坐標為(2m,2m2-6m)．

圖7

3 關于位似的幾點認識

·關注位似的內容價值

(1)強化幾何圖形位似的認識

作為初中四大變換之一的位似，它是教師最“不待見”的，但它又與平移、旋轉、軸對稱一樣提升著學生對圖形的空間認識．位似變換在簡單的圖形內容易被掌握，但在稍微復雜的圖形中，“數”的關系就顯得比較隱蔽，如位似比往往被學生忽視，隱含關系更是讓學生“一籌莫展”，因而教師有必要強化學生對位似變換的認識．一要通過觀察認識位似中心，突出對應點連線的交點；二是通過畫圖強化位似比，突出放大、縮小與方向．

(2)深化函數圖象位似的認識

初中教材只是針對幾何封閉圖形探討位似，對開放性的圖形的位似幾乎未涉及．如所有的拋物線都位似，雙曲線也是位似的，作為教師應該要深化認識．

(3)了解位似的廣義概念

·關注位似的運用價值

位似是特殊的變換，在數學內外部和生活中有著重要應用．

(1)在數學內部的運用

文[6]給出了運用位似證明點共直線、點共圓和直線共點；文[7]指出位似在函數、作圖和證明中的運用．以上充分揭示了位似的數學方法價值．

(2)跨學科的運用

事實上，位似在物理、美術、地理等學科中也有著較為廣泛的應用．如物理中透鏡成像就離不開位似，位似研究的方法對美術學科對比研究透視有著借鑒意義．

(3)在生活中的運用

位似在生活中的運用非常豐富，如測量建筑物高度、河岸寬度、物體長度等常用到位似原理；例1也有著現實意義，可解決生活問題：在兩條不相平行的道路上如何確定兩點位置，建設一條經過點P的最短直路．

·關注位似的思維價值

(1)位似變換體現數形結合思想

位似是由“雙變量”控制的，|k|的大小決定圖形放大與縮小的程度，位似中心影響著變換后的位置．它的研究過程對后續學習極坐標、函數有著積極的意義，可激發學生自覺運用位似變換解決問題的意識．

(2)位似變換體現關聯思想

數學學科素養中的關鍵能力之一就是相互 關聯，而位似變換恰是培養此能力的重要數學 資源．一是體現在變換前后兩個圖形之間的關聯，它們包含著許多特殊的位置關系和數量關系， 如對應點的連線交于一點，角之間、線段之間的特殊數量關系等；二是體現在位似變換與其他變換之間的關聯，如與旋轉變換結合形成位似旋轉變換，與軸對稱變換結合形成位似翻折變換，它們 有著重要的思維價值，在文[8]中有具體的例子說明．