正確理解彈性勢能的概念

摘 要：分析了經典彈性勢能概念的局限性，重新定義了彈性勢能，并且推廣給出了勢能的一般概念。

關鍵詞：輕質彈簧;彈性勢能;勢能;質量

中圖分類號：O313.1 文獻標識碼：A 文章編號：1671-2064（2020）08-0237-02

1問題的提出

現在一般力學教材給出彈性勢能的定義為——發生彈性形變的物體的各部分之間，由于有彈力的相互作用，也具有勢能，這種勢能叫做彈性勢能（elastic potential energy）。在工程中又稱“彈性變形能”。例如被壓縮的氣體、拉彎了的弓、卷緊了的發條、拉長或壓縮了的彈簧都具有彈性勢能。同一彈性物體在一定范圍內形變越大，具有的彈性勢能就越多，反之，則越小。彈性勢能是存儲在材料或物理系統的構造中的潛在機械能，因為執行工作以扭曲其體積或形狀。當需要壓縮和拉伸或大體上以任何方式變形時，彈性能量就會發生。彈性理論主要發展為固體和材料力學的形式（注意，拉伸橡皮筋所做的工作不是彈性勢能的一個例子，它是熵彈性的一個例子）彈性勢能方程用于機械平衡位置的計算。在數學上，方程可以表示為：，這個定義其實是不完善的，下面首先以彈簧的彈性勢能為例說明一下這個問題，上述概念只談到了彈簧的彈性勢能，沒有涉及彈簧的動能，不少人理解為忽略彈簧的動能，只研究其勢能。可是這樣會造成矛盾，例如在地面系把一個彈簧壓縮后放入真空中，它的勢能不斷變化，如果不考慮彈簧的動能，顯然不滿足能量守恒定律。根據愛因斯坦質能方程E=mc2，能量一定與質量成正比，無法體現。

2問題的解決

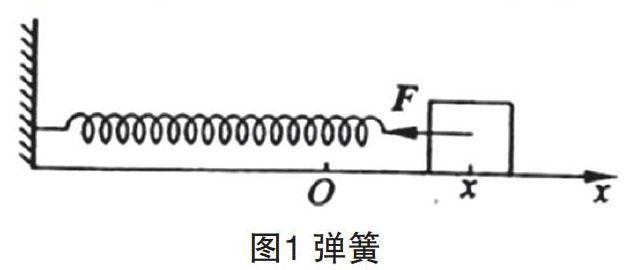
從上面的分析可以看出只具有彈性勢能而不具有動能的彈簧是不存在的，彈弓和彎曲的樹枝等發生彈性形變的物體具有勢能，在變化的過程中也具有動能，實踐中可以忽略動能，是近似處理。輕質彈簧在忽略彈簧質量的同時也忽略了彈簧的勢能和動能，現在部分中學教材甚至高考中研究輕質彈簧的彈性勢能，這是不準確的，嚴格講應該表述為與輕質彈簧接觸質點的彈性勢能，例如在彈簧振子中，如果這樣表達彈性勢能，就可以看出彈性勢能屬于質點，而不是屬于彈簧。這樣可以發現勢能與質量成正比，符合質能方程的要求。在大中學階段可以只研究質點的彈性勢能，作為專家可以研究彈簧的彈性勢能。當考慮彈簧質量時，可以宏觀考慮為若干個受彈力作用的質點，必須研究彈簧的動能了，也可以把彈簧的質量合并到質點中去，必須考慮彈簧的質量是否均勻等因素，不是簡單相加，見圖1。

我們可以把牛頓第二定律和歐姆定律進行類比，合外力相當于電壓，質量相當于電阻，加速度相當于電流。導線抽去電阻、電感等屬性后用電器的電壓等于導線兩端的電壓一樣。類似于不考慮電阻、電感等屬性的導線不能承擔電壓和消耗能量一樣，輕質彈簧不能單獨承受力[1]，也不能儲存能量[2]，千萬不要認為彈簧振子中彈簧具有勢能，忽略動能。這樣動能定理就不成立了，外力做功了，動能卻沒有變化。有人認為彈簧振子中彈簧具有微弱的質量，忽略質量，這顯然是錯誤的。這就像我們忽略摩擦，再考慮微弱摩擦力一樣的荒唐。沒有質量和具有勢能二者不可兼容，理論上不存在運動過程中只具有勢能不具有動能的物體，實驗中的彈簧是忽略動能（近似處理）。有人認為理想的彈簧只具有勢能不具有動能，是一個彈性體，但是這個假設違背物理學的基本原理，例如文獻[3]構造了一種只具有勢能而不具有動能的彈簧，是荒謬至極的。彈簧振子不是質點+實物彈簧，而是質點受到線性回復力，在水平面上受穩定約束的彈簧振子運動模型，實質上是一個與距離r成正比有心力作用下質點的運動問題[4]。在彈簧振子問題中，是一個完整、理想、雙側束的質點，約束力不改變質點的機械能;考慮彈簧質量，是具有完整、理想、雙側束的質點系，約束力也不改變系統的機械能。

趙凱華認為：研究一個規律的表述所具有的對稱性，并設法消除某種不對稱因素，從而使其規律的表述具有更多的對稱性，這無疑是有重要意義的。因為它不僅滿足人類對于美（對稱，和諧）的心理追求，而且更重要的是使表述的規律具有更大的普遍性。由于質點受到萬有引力而具有的勢能叫引力勢能，由于質點受到重力而具有的勢能叫重力勢能，而把彈性勢能定義為由于彈性形變具有的勢能不具有和諧性，因為彈簧振子中質點具有彈性勢能而沒有形變。如果把彈性勢能定義為由于質點受到保守彈力作用（并非所有彈力都是保守力，例如非彈性碰撞中的彈力，嚴格講彈力都不是保守力，當只考慮彈力的大小和方向，而忽略形變的影響時才是保守力，例如斜面的支持力。）而具有的勢能叫做彈性勢能就比較完整了，不但包括彈簧振子中的彈性勢能[5]，也包括具有質量的彈簧、彈弓、弓箭等彈性勢能，甚至包括光滑斜面上的滑塊受到的彈力——支持力等具有的彈性勢能[6]和單擺的擺錘受到擺線的約束力具有的勢能等。質點只要受到彈力作用就具有彈性勢能，不一定發生彈性形變，例如小滑塊在光滑斜面上下滑，斜面的形變為0，質點依然具有彈性勢能[6]。有人說沒有形變哪來的彈力，確實這樣，一個物體放在水平地面上受到支持力是彈力，但是我們不必考慮形變，力學中不必考慮力的性質的來源，重力來源于萬有引力，摩擦力還來自于電磁力呢？我們計算摩擦力時從來不考慮電磁力的問題，研究質點的重力時也不考慮萬有引力。

由于質點受到保守彈力作用（并非所有彈力都是保守力，例如非彈性碰撞中的彈力）而具有的勢能叫做彈性勢能，由于質點受到萬有引力而具有的勢能叫引力勢能，由于質點受到重力而具有的勢能叫重力勢能，由于質點受到浮力而具有的勢能叫浮力勢能[7-17]，由于質點受到支持力而具有的勢能叫支持力勢能，由于質點受到約束力而具有的勢能叫約束力勢能、、、、、、，可以給出勢能的一般定義——由于質點受到有勢力而具有的能量叫做勢能，勢能的定義式為dEp=（-f）·dr（與等價），當有勢力不顯含時間（即為保守力）時，勢能也可以稱為位能，（筆者注：類似地可以定義由于電荷受到電場力而具有的勢能叫做電勢能，從勢能的定義式可以看出單質點的勢能是坐標的函數，不具有伽利略變換的不變性），這樣更具有對稱性與和諧性。本文把勢能和位能區別開來，位能是勢能的一種情形，對于保守力二者是一致的，對于顯含時間的力是有區別的，此時只有勢能沒有位能。經典力學教材把二者等同起來，認為只有保守力才存在勢能，可是有關文獻又指出當勢能不顯含時間時力是保守力，二者之間存在矛盾，按照本文的觀點矛盾自然解決。根據dEp=（-f）·dr（與等價）可以得出只要力場是空間坐標的函數，此力一定是保守力，耗散力和顯含時間的力不是空間坐標的函數，是非保守力。

根據dEp=（-f）·dr可以得出力場不顯含時間，勢能一定不顯含時間，這里沒有時間變量t，文獻[18]的觀點是完全錯誤的，只要質點受到保守力就具有勢能，具體數值與勢能零點的選擇有關，只要勢能零點相對于觀察者不變即可，文獻[18]錯誤的根源在于勢能零點的選取錯誤。機械能守恒定律是時間均勻性的體現，顯含時間的力場能量不守恒。僅僅適用于彈簧振子中質點的彈性勢能，而且不適用于所有的慣性系[5]，不適用于彈簧的彈性勢能。趙凱華、羅蔚茵在其《新概念物理教程——力學》一書中說：“追求某種東西守恒是產生科學思想不可少的條件，科學家們常有尋找守恒的強烈愿望，與運動相聯系的守恒量長久以來就是物理學家尋找的目標，從守恒的觀點來看，勢能的概念是不能沒有的[19]。”英國著名物理學家狄拉克在被問及：是怎樣得到那著名的相對論量子方程時，回答得很干脆，“我發現它美！”這種科學美也與對稱性密切相關， 愛因斯坦將之發揮到了極致。在他以前，科學家是從定律中發現對稱性，愛因斯坦反其道而行之──從對稱性中發現定律。他的廣義相對論就是一個范例：從引力與加速度等效原理出發，憑協變對稱性就能寫出引力方程。這種從對稱性中找定律的方法被沿用至今，在物理學的前沿探索中發揮著越來越大的作用。所以科學家不只是求真，也在尋美[20]，愛因斯坦曾經講過：“相信世界在本質上是有秩序的和可認識的這一信念，是一切科學的基礎。我永遠不會說我真正懂得了自然規律的簡單性所包含的意思。”

現在不少力學教材在表述力的作用效果時一方面指出“力是改變物體運動狀態的原因”，另一方面指出“力是物體產生形變的原因”，一些初學者往往認為力的作用效果有兩種，其實二者本身是一致的，“力是改變物體運動狀態的原因”此時物體看做質點。“力是物體產生形變的原因”此時物體不能看做質點，組成物體的各個質點的運動狀態也發生了改變，物體產生形變只是一個宏觀效果，所以可以統一表達為“力是改變質點運動狀態的原因”，牛頓就說過，自然界喜歡簡單化，而不喜歡用什么多余的原因以夸耀自己。追求簡單性是經典科學奮斗的目標，也是推動它獲取成功的動力。開普勒以三條簡明的定律揭示了看似復雜的太陽系行星運動，牛頓更是用單一的萬有引力說明了千變萬化的天體行為。因而現代科學是用簡單性解釋復雜性，這就隱去了自然界的豐富多樣性，普朗克曾經講過：“在科學史上，一個新概念從來都不會是一開頭就以其完整的最后形式出現，象古希臘神話中雅典娜一下子從宙斯的頭里跳出來那樣。”

參考文獻

[1] 趙志棟，陳光紅.輕彈簧之“困境”[J].物理通報，2016（5）：98-101.

[2] 唐龍.例說能量的系統性和相對性[J].物理教師，2016（6）：18-19.

[3] 朱如曾.彈簧振子相對于運動慣性系的機械能不守恒——關于“對一道中學生物理競賽試題答案的商榷”的商榷[J].物理通報，2015（4）：84-87.

[4] 李陽，王宏，韓艷玲.與r的一次方成正比有心力作用下質點的運動研究[J].物理通報，2015（12）：4-7.

[5] 李學生，師教民.對一道中學生物理競賽試題答案的商榷[J].物理通報，2014（9）：119-120.

[6] 張翠.斜面上下滑滑塊機械能守恒問題新解[J].物理通報，2016（9）：115-117.

[7] 楊子立.關于浮力的幾點分析[J].綏化師專學報，2001（6）：

99-100.

[8] 胡毅，阮士軍.關于浮力的幾點討論[J].鄖陽師范高等專科學校學報，2004（12）：7-8.

[9] 張曉森，肖玉林.一類浮力問題的規律性分析[J].中學物理，2011（5）：16-17.

[10] 鄭金.彈性勢能公式的妙用[J].新課程（中），2011（8）：143.

[11] 屈志紅.浮力是否是保守力[J].錦州師范學院學報，2002（12）：67-68.

[12] 照那木拉.關于浮力場概念的引入及其P的力能二重性[J].內蒙古民族大學學報（自然科學版），2002（6）：558-560.

[13] 胡義嘎.浮力是保守力[J].赤峰學院學報（自然科學版），2012（11）：18.

[14] 羅臘春.浮力與浮力做功[J].物理教師，2015（5）：96-97.

[15] 胡義嘎.浮力勢能[J].內蒙古師大學報自然科學（漢文）版，1999（12）：31-33.

[16] 胡義嘎.浮力勢能及其四種表示方法[J].赤峰教育學院學報，2003（5）：104-106.

[17] 孫石，宋兆麗.水球浮力勢能及彈射速度的計算[J].吉林師范大學學報（自然科學版），2003（8）：108-109+113.

[18] 朱如曾.力場與時間有關系統的功能定理及其應用[J].大學物理，2016（10）：11-16.

[19] 趙凱華，羅蔚茵.力學[M].北京：高等教育出版社，1965.

[20] 沈致遠.對稱趣談.文匯報[N].2009-7-3-9.