高中數學數列求和的常用方法

◎龔 言 李 敏 （.北華大學數學與統計學院，吉林 吉林 303；.吉林省磐石市第五中學校，吉林 磐石 3300）

數列求和的常用方法有：公式法、分組求和法、倒序相加法、裂項相消法、錯位相減法、并項求和法.

一、公式法

此方法具有很強的針對性，觀察數列通項公式，如果一個數列是等差數列或是等比數列，即可直接用等差或等比數列的前n項和公式求解.

例1已知數列｛an｝是等比數列，公比q＜1，且a2＝2，a1＋a2＋a3＝7.

（1）求｛an｝的通項公式；

（2）設bn＝log2an，求數列｛bn｝的前n項和.

解（1）由已知，得

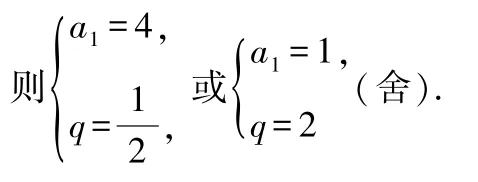
所以an＝ 23－n.

（2）因為bn＝log2an＝log223－n＝ 3－n，所以數列｛bn｝是以2 為首項、－1 為公差的等差數列.

設數列｛bn｝的前n項和為Tn，

二、分組求和法

分組求和法一般適用于通項公式為如下兩種形式的數列：

（1）若an＝bn±cn，且｛bn｝，｛cn｝為等差數列或等比數列，可采用分組求和法求｛an｝的前n項和.

｛bn｝，｛cn｝是等比數列或等差數列，可采用分組求和法求和.

例 2已知數列｛an｝的通項公式an＝ 2n＋n.求a1＋a2＋a3＋…＋an的值.

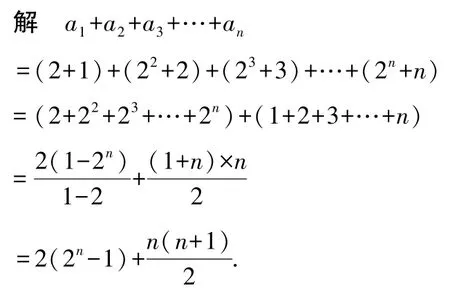
反思與感悟一些數列通過適當分組，可以得到兩個或幾個等差數列或等比數列，進而利用等差數列或等比數列的求和公式分別求和，從而得出原數列的和.

三、倒序相加法

如果一個數列｛an｝，與首末項等距的兩項之和等于首末兩項之和，那么求這個數列的前n項和可用倒序相加法，如等差數列的前n項和即用此法推導的.

例 3已知f（99）＋f（100）的值.

解由題意，得

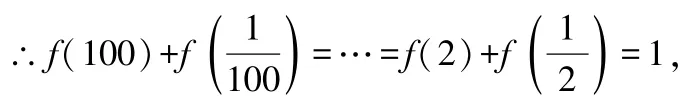
四、裂項相消法

如果一個數列的通項可拆成兩項之差，然后重新組合，使中間的項可以相互抵消，那么求此類數列前n項和用裂項相消法，裂項相消求和經常用到的拆項公式如下：

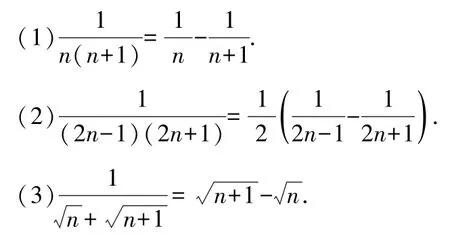
例4求的和.

解∵此數列的前n項和

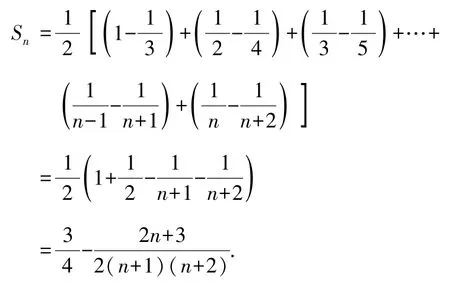
反思與感悟若數列的通項公式可以化為f（n＋1）－f（n）的形式，則在數列求和時，就可以采用裂項相消法.要注意相消后的項要對稱，若前面留下兩項，則后面也要留下兩項.

五、錯位相減法

若一個數列的各項是由一個等差數列和一個等比數列的對應項之積構成的，則這個數列的前n項和即可用此法來求，如等比數列的前n項和公式就是用此法推導的.

例 5已知數列｛an｝的通項公式an＝2n－1（n∈N?），

數列｛bn｝滿足

求｛bn｝的前n項和Tn.

解設

則當n≥2 時，

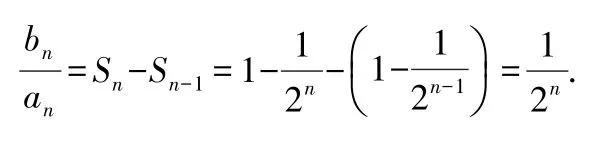
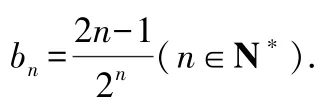
所以有

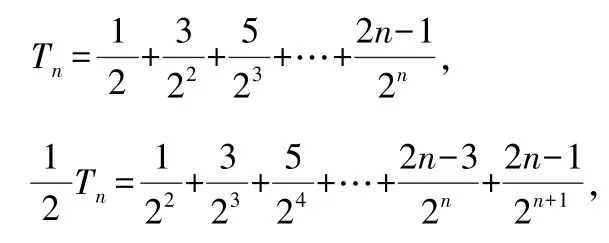
兩式相減，得

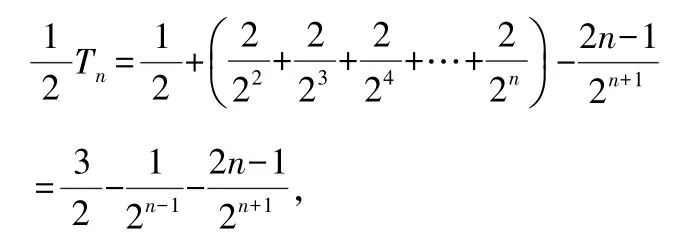
所以

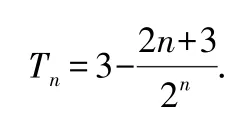
反思與感悟用錯位相減法求和時應注意：（1）要善于識別題目類型，特別是等比數列公比為負數的情形；（2）在寫出“Sn”與“qSn”的表達式時應特別注意將兩式“錯項對齊”以便下一步準確寫出“Sn－qSn”的表達式.若公比是個參數（字母），則應先對參數加以討論，一般情況下分等于1 和不等于1 兩種情況分別求和.

六、并項求和法

若一個數列的前n項和可兩兩結合求解，則稱之為并項求和.形如an＝（－1）nf（n）的類型，可采用兩項合并求解.

例 6求Sn＝－1＋3－5＋…＋（－1）n（2n－1）.

解當n為奇數時，

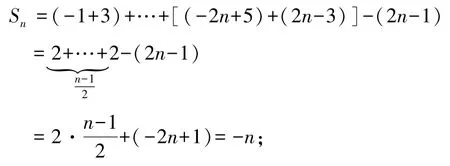
當n為偶數時，

綜上，

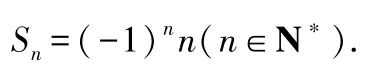
反思與感悟當數列中的項正、負相間時，通常采用并項求和法，但應注意對n的取值的奇偶性進行討論.其結果有時可以統一書寫，有時要分段書寫.

總而言之，在求數列的前n項和的具體問題中，首先要認真觀察這個通項公式的特征，然后選擇恰當的方法，在平時的學習和訓練中，學生要注意舉一反三，從一道題目解答過程中尋求同一類題目的共性特征，從而提高自己的解題能力.