基于集成學習的中國股票市場多因子策略研究

牛曉健，魏宗皓

(復旦大學，上海 200433)

一、引言

自Fama-French三因子模型提出以來，多因子模型逐漸成為一種主流的量化投資方法。多因子模型主要通過因子收益和因子暴露對股票在橫截面上的收益率結構進行刻畫，但在具體的建模過程中，Fama-French模型和Barra模型采用了兩種不同的思路。在Fama-French模型的框架下，首先依據某一特征構建股票組合，計算多空組合的收益率作為因子收益，然后再時序上進行回歸得到因子暴露，進而得到預期的收益率結構。而在Barra多因子模型的框架下，則先有因子暴露，再將當期的因子暴露和未來一期的股票收益進行回歸得到因子收益。Barra多因子模型是典型的橫截面回歸，以最小化所有股票的定價錯誤為目標，通過檢查所有殘差項聯合起來是否為零來判斷模型的好壞。根據最新的Barra China Equity Model (CNE5)操作手冊，Barra多因子模型中包含三類因子：1個國家因子、32個行業因子和10個風格因子。其中國家因子對應的上述方程中的截距項，所有股票對國家因子的暴露為1。風格因子細分為Size、Beta、Momentum、Residual Volatility、Book-to-Price、Non-linear Size、Earnings Yield、Liquidity、Leverage和Growth。

人工智能、機器學習的興起為多因子模型構建提供了新的思路和方法，越來越多的學者和業界的投資者將機器學習算法引入多因子模型中來，取得了不錯的效果。但是單一的機器學習算法，如支持向量機、Logistics、決策樹等，在處理復雜的金融數據時經常會產生過擬合的問題，導致樣本內和樣本外的策略表現差距較大。本文將多因子選股當作分類問題處理，使用隨機森林、Adaboost和XGboost等集成學習算法進行滾動訓練，并以中證800指數成分股作為股票池，對模型表現進行回測，以驗證集成學習算法在多因子模型上的適用性。

二、文獻綜述

Eugene F. Fama 和 Kenneth R. French提出著名的三因子模型，將橫截面股票收益率的差異歸結為三個因素：市場因素、規模因素和賬面市值比因素。基于這三個因素，Eugene F. Fama和Kenneth R. French構建出三個關鍵的因子：市場組合的超額收益、小市值股票組合和大市值股票組合的收益率之差、高賬面市值比組合和低賬面市值比組合的收益率之差[1]。三因子模型被認為開辟了多因子研究的先河，為后來的多因子模型研究提供了重要的思路和方法。Eugene F. Fama 和 Kenneth R. French在三因子模型的基礎上，引入了盈利水平因子和投資風格因子[2]，提出了五因子模型，模型的解釋力進一步提高。在此之后，學者和投資者們更多的關注因子的解釋力。比如Clifford S. Asness和Andrea Frazzini等從盈利性、增長性、安全性和派息率四個維度綜合分析上市公司的質量，并通過綜合打分的方法得到一個擁有多種度量維度的質量因子，證明了通過做多高質量股票做空低質量股票，可以獲得顯著的風險調整后收益[3]。Frazzini和Pedersen指出由于有約束的投資者偏好高beta資產，導致高beta的資產常常伴隨著低alpha，根據這一特點，Frazzini和Pedersen構建了一個beta套利因子(BAB)，即買入有杠桿的低beta資產并賣出高beta資產，可以獲得顯著為正的風險調整后收益[4]。范龍振、余世典通過對1995年7月至2000年6月全部A股股票月收益率的研究，證明了與國外大多數資本市場一樣，我國的A股市場存在顯著的市值效應、賬面市值比效應和市盈率效應。同時，我國的A股市場還存在顯著的價格效應[5]。楊炘和陳展輝驗證了Fama-French三因子模型在我國A股市場上的適用性，指出我國A股市場存在顯著的公司規模效應和股東權益賬面市值比效應，市場因素、規模因素和賬面市值比因素可以完全解釋A股股票收益率的截面差異[6]。徐景昭利用回歸的方法對使用市盈率、ROE增長率、資產負債率、月平均換手率等11個常見因子進行有效性檢驗，從中篩選出市凈率、ROE增長率、資產負債率、月平均換手率、市值等5個有效因子，分別構建了基本的多因子模型、基于貨幣周期的行業輪動多因子模型以及基于固定效應下的多元回歸模型，驗證了多因子模型在我國市場的有效性[7]。

隨著人工智能的興起，一些研究者不再局限于因子研究和多因子模型的有效性檢驗，而是另辟蹊徑，對機器學習算法在量化投資領域進行了探索。Eric H, Keith L和Chee K指出了傳統多因子選股存在的問題，并提出應用CART(Classification and Regression Tree)的方法進行選股。該方法以科技股為研究對象，從估值、基本面營利性、一致預期和價格動量四個方面選擇了Sales-Price、Cash Flow-Price、EPS-Price、ROA等6個因子作為解釋變量，以個股收益率與截面收益率的中位數之差將截面股票劃分為兩個類別：out-perform和under-perform，并將其作為標簽，分別用靜態樹和動態樹的方法進行訓練和預測，驗證了動態樹相對于靜態樹存在邊際改進，暗示了不斷修正建樹樣本的動態樹模型可以更好把握市場的變動規律[8]。錢穎能、胡運發應用樸素貝葉斯分類算法來訓練上海證券交易所股票的會計信息，并獲得了超越市場指數的超額回報[9]。郭文偉使用了支持向量機的股市風格輪換策略[10]。方匡南、吳見彬、朱建平、謝邦昌系統地總結了隨機森林方法的原理與應用，并介紹了隨機森林的兩種衍生模型：隨機生存森林和分位數回歸森林[11]。文章全面總結了隨機森林方法的優勢，如bootstrap重抽樣的方法利于提高模型對噪聲和異常值的容忍度、袋外數據便于評價組合樹的泛化能力、運算速度遠快于Adaboost等，為基于機器學習的量化選股提供了重要方法論。王淑燕、曹正鳳、陳銘芷構建了凈資產收益率、總資產收益率、市凈率、EPS一致預期等16個因子作為解釋變量，利用股票在時間序列上的漲跌幅均值和行業漲跌幅均值構建了響應變量，通過隨機森林方法預測未來股票的漲跌[12]。焦健、趙學昂、葛新元基于我國A股的電子和信息技術兩個行業的股票數據研究了CART(Classification and Regression Tree)的選股效果，并在傳統的CART模型基礎上進行樹的修剪與過濾，最終形成行業選股框架。

三、多因子模型理論

多因子模型研究的是股票收益率在橫截面上的差異。多因子模型的發展可追溯到William Sharpe的CAPM模型和Ross的APT模型。CAPM模型將股票收益率差異歸結為系統性風險，即貝塔系數[13]。APT理論則認為資產的收益率由一系列影響因素及相應的因素敏感性決定，當市場達到均衡時，均衡的預期收益率是因素敏感性的線性函數[14]。但APT理論并沒有對影響因素進行進一步的闡述。直到Fama-French三因子模型和Barra模型的出現，多因子模型的理論體系逐漸完善，并以兩種模型為基礎，形成了兩種主流的多因子研究體系。

Fama-French和Barra的多因子模型均涉及三個關鍵的概念：預期收益率、因子收益、因子暴露。一個典型的多因子模型可表示為如下形式：

(1)

在Fama-French的多因子模型框架下，首先依據某一特征構建股票組合，計算多空組合的收益率作為因子收益，然后再時序上進行回歸得到因子暴露，進而得到預期的收益率結構。以經典的三因子模型為例，模型的形式是：

Ri,t-Rf=αi+bi(RM,t-Rf)+si(SMBt)+hi(HMLt)+εi,t

(2)

根據該式，股票的超額回報可以被三個因子的超額回報率解釋：①市場組合超額回報RM,t-Rf，RM,t為t期市場組合的超額回報，Rf為無風險利率。②規模因子SMBt。③賬面市值比因子HMLt。在Fama-French的框架下，因子代表的是投資組合的收益率。具體來看，首先按照市值對因子進行排序，并以中位數為界，分成兩個組合small和big。然后再根據賬面市值比BE/ME對兩個組合分別排序，按照30%、40%、30%的比例進一步劃分，得到S/H、S/M、S/L、B/H、B/M、B/L六個組合。SMB代表小市值組合(S/H、S/M、S/L)和大市值組合(B/H、B/M、B/L)的收益率之差，HML代表的是高賬面市值比組合(S/H和B/H)和低賬面市值比組合(S/L和B/L)的收益率之差。得到因子收益后，按照如下形式進行時間序列回歸，得到因子暴露：

(3)

(4)

Black、Jensen和Scholes在此基礎上給出了計算因子預期收益的簡單方法，即因子收益率在時間序列上的均值就是因子的預期收益率。所以根據因子暴露和因子的預期收益率，可以得到股票的預期收益率，從而做出投資決策。通過GRS檢驗等統計檢驗方法，檢驗所有股票的αi聯合起來是否為零，可以評價多因子模型的解釋力。

在Barra的多因子模型框架下，因子并不是投資組合的收益率，而是個股的基本面數據或是行情數據。典型的Barra模型可以表示成如下形式：

(5)

根據Barra China Equity Model (CNE5)操作手冊，Barra多因子模型中包含：1個國家因子、32個行業因子和10個風格因子。其中國家因子對應的上述方程中的截距項，所有股票對國家因子的暴露為1。行業因子和風格因子對應上式中的ft，其中風格因子包括Size、Beta、Momentum、Residual Volatility、Book-to-Price、Non-linear Size、Earnings Yield、Liquidity、Leverage和Growth。

機器學習的出現為建立多因子模型提供了新的方法。比如用SVM、Decision Tree、Random Forest等算法代替線性回歸進行多因子回歸。再比如將股票的預期的漲跌狀態(0/1變量)作為被解釋變量，利用SVM、Logistic等分類算法構建多因子模型，通過F1-score和AUC等來評價多因子模型的好壞。

四、集成學習理論

集成學習本身并不是一種單獨的機器學習算法，而是通過訓練多個弱學習器，按照一定的方式進行組合，得到最終的強學習器。至于弱學習器的算法，可以有多種選擇，最常用的是Decision Tree。

Bagging和Boosting是集成學習算法的兩大派別。Bagging為并行算法，同時訓練多個弱學習器，各個學習器間互不影響，最終通過大多數投票等方法匯總各個弱學習器，得到最終的強學習器。Bagging算法的代表是隨機森林。Boosting為串行算法，各個弱學習器間存在較強的依賴關系，通過給分類錯誤的樣本以較高的權重來不斷降低分類的錯誤率，最終將全部弱學習器加權得到最終的強學習器。Boosting的代表是Adaboost和XGboost。

(一)隨機森林算法

隨機森林是由Leo Breiman在2001年論文《Random Forests》中提出的一種集成學習方法[15]，這一算法是由多個隨機子集(Bootstrap數據集)生成的決策樹實例組成，稱之為“隨機森林”。

1.決策樹原理及數學表達

隨機森林算法基于基本的決策樹(Decision Tree)模型。所謂決策樹模型，是通過多個特征進行分類決策，在每個節點處，按照信息增益(Information Gain)最大化的方向進行分裂，得到下一層的節點，直至分裂至最終的葉子節點。常用來度量信息增益的方式有以下兩種：

(1)Gini系數

Gini系數又叫做Gini不純度，用來表示一個隨機選中的樣本在子集中被錯分的可能性。Gini系數為這個樣本被選中的概率乘以它被錯分的概率，可表示成如下形式：

(6)

當一個節點中所有的樣本都是同一類別時，Gini系數為0。

其中pk為數據集D中的樣本點屬于k類別的概率，Gini系數可理解為隨機從數據集中取出兩個樣本，其類別標記不一致的概率。Gini系數越小說明數據集的純度越高。

采用Gini系數度量時，D節點根據特征A進行分裂時，分裂后的Gini系數可以表示如下形式：

(7)

其中，Gini(left)和Gini(right)分別表示左邊子節點和右邊子節點的Gini系數。按特征A進行分裂時，信息增益可以表示為：

IGGini=Gini(D)-Gini(D,A)

(8)

(2)信息熵

熵最早源自于熱力學，用來度量分子的混亂程度，熵值越大表示系統越混亂。而信息熵則借鑒了熱力學中熵的概念，信息熵越大，集合越混亂，換言之，純度更低。信息熵可表為如下形式：

(9)

采用信息熵度量時，D節點根據特征A進行分裂時，分裂后的信息熵可以表示如下形式：

(10)

其中，H(left)和H(right)分別表示左邊子節點和右邊子節點的信息熵。按特征A進行分裂時，信息增益可以表示為：

IGH=H(D)-H(D,A)

(11)

決策樹模型可以理解為每個節點不斷地朝著信息增益最大的方向分裂為兩個子節點，直至滿足達到最大深度、葉子節點的Gini系數足夠小、葉子節點中的樣本數小于最小分類樣本這三個條件中的任意一個，則停止分裂，得到最終的決策樹模型。

2.隨機森林

隨機森林是一種基于信息論和統計抽樣理論的分類算法，屬于集成學習的Bagging派系，除Bagging外，集成學習還有Boosting的方法。

從上述的算法介紹可以看出，隨機森林包含兩個隨機過程：訓練樣本隨機和特征隨機。這一特點使得隨機森林模型可以有效地防止過擬合，提高模型得泛化能力。

(二)AdaBoost算法

Schapire和Freund在1995年提出Adaboost(adaptive boosting)算法。該算法將弱分類器以串行的方式集合起來。在初始訓練時，每個樣本被賦予相同的權重，對于分類錯誤的樣本，提高其權重。最后以更新權重后的樣本作為第二次訓練的輸入集，以此類推，得到各個弱分類器，最終通過加權匯總，得到最終的強分類器。

1.用帶權重的樣本訓練弱學習器φm(x)；

2.計算第m個弱分類器在權重分布ωm上的誤差：

(12)

其中I表示指示函數，滿足條件時返回1，否則返回0。

3.計算第m個分類器的權重：

(13)

其中τ是學習率超參數。該分類器的誤差率越低，它所占的權重就越高，如果它只是隨機猜測，那么它的權重接近于零，如果誤差率比隨機猜測還要低，則它的權重為負。

4.更新訓練樣本的權重分布：

(14)

其中Zm是歸一化參數，

(15)

通過Zm的表達式可以看出，被分類正確的樣本獲得了更低的權重，分類錯誤的樣本獲得了更高的權重。

5.重復迭代，用新的權重分布訓練新的分類器。當達到迭代次數要求或者得到分類準確率達到要求時，算法停止。最終按αm對各個弱分類器加權，得到最終的強學習器:

(16)

Adaboost的弱分類器同樣采用上一小節中介紹的決策樹模型，除此以外，常用的還有以Logistics回歸為基分類器構建的Adaboost模型，即LR_Adaboost。本文使用的是基于CART決策樹的Adaboost模型。

(三)XGBoost算法

1.GBDT算法的原理及數學表達

GBDT算法即Gradient Boosting Decision Tree，可以分為Gradient Boosting和Decision Tree來分別看待。Gradient Boosting不是一種具體的算法，而是一種優化的理念。比如對于給定訓練集{(x1,y1),(x2,y2),(x3,y3)……(xn,yn)}，Gradient Boosting可表示為如下過程：

(1)首先估計使損失函數極小化的常數值：

(17)

其中L表示損失函數(Loss Function)，θ代表弱學習器。

(2)計算損失函數的負梯度：

(18)

(3)得到{(x1,rm,1),(x2,rm,2),(x3,rm,3)……(xn,rm,n)}，進行訓練得到：

(19)

(4)計算最優步長：

ρm=argminρL(yi,fm-1(x)+ρθm)

(20)

(5)完成模型的更新：

fm(x)=fm-1(x)+ρmθm

(21)

(6)重復(2)到(5)，直至達到既定的迭代次數或滿足精度要求。

Gradient Boosting僅給出了一種優化框架，并沒有指定具體的算法。GBDT(Gradient Boosting Decision Tree)則是應用Gradient Boosting框架的一種具體算法，該方法采用決策樹(Decision Tree)作為弱學習器，通過不斷迭代，得到最終的強學習器。

而對于二元分類問題，可以定義損失函數(Loss Function)為對數損失函數：

L(y,f(x))=log(1+exp(-yf(x)))

(22)

帶入上述Gradient Boosting的優化框架，并以決策樹作為弱分類器進行訓練，最終得到強分類器。

2.XGboost的原理及數學表達

XGboost算法是對梯度提升決策樹(GBDT)算法的改進和提升，這里介紹基于CART決策樹的XGboost算法。該算法的基本框架與GBDT相似，但在構造新樹時有所不同，具體總結為以下幾點：

(1)XGboost的損失函數加入了正則化項，可表示成如下形式：

(23)

(2)訓練第t棵CART樹時，要最小化obj(t)，而obj(t)進行簡單變換后又可以表示成如下形式：

(24)

其中const表示常數，即前t-1棵樹的復雜度。對上式進行二級泰勒展開，可得：

(25)

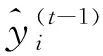
(26)

(3)obj(t)中的正則項使用如下形式：

(27)

其中T代表CART樹的葉子節點數目，ωj表示每個葉子節點上的得分，γ和λ為懲罰系數，數值越大代表懲罰力度越大。

(4)對obj(t)進行簡單變換，改變內外求和順序，可得：

(28)

上式是關于ωj的二次函數，可直接求得極小值點：

(29)

以及目標函數得極小值：

(30)

obj*代表了樹的結構的好壞，該值越小，樹的結構越好。利用貪心算法枚舉不同樹的結構，挑選出最好的樹。具體來說，對于現存得每一個葉子節點，掃描所有的額切分點，衡量切分點的標準如下式所示：

(31)

Gain表示單節點的obj*與切分后兩個節點的obj*之和的差值，Gain越大說明越值得切分。

3.XGboost算法的優勢

(1)傳統的GBDT算法僅使用了損失函數(Loss Function)的一階導數，而XGboost對損失函數進行了泰勒展開，用到了一階導數和二階導數。XGboost支持自定義的損失函數，只要保證損失函數在數學上是二階可導的。

(2)XGboost在損失函數中引入了正則項，用于控制樹的復雜度，有利于防止過擬合，減小模型的方差。

(3)XGboost支持特征抽樣(借鑒了隨機森林的思想)，在構建弱學習器時僅使用抽樣出的部分特征來訓練，減小過擬合風險。

(4)XGBoost在處理特征的層面上支持并行。訓練決策樹最耗時的一步就是對各個特征的值進行排序(為了確定最佳分割點)并計算信息增益，XGBoost對于各個特征信息增益的計算可以在多線程中進行，大大提高了模型的訓練速度。

五、候選因子有效性檢驗

本文使用的候選因子包括基本面因子和量價因子，數據均取自天軟數據庫，時間區間為2010年1月至2020年1月。基本面因子為財務指標，包含盈利能力、收益質量、償債能力、成長性、估值水平和公司規模6個維度，如表1所示。量價因子既包括常見的收益率反轉、波動率和換手率。如表2，也包括利用遺傳算法挖掘的部分因子。遺傳算法方面，本文借鑒了Github上Genetic Programming算法的框架，并對這一算法進行了深度改造，重新編寫運算符、適應度計算、表達式解析等模塊，使其適用于因子挖掘，相關參數設置如表3。

本文使用IC和信息比率作為因子有效性的評價標準，并根據因子間的相關度，對部分因子進行剔除。最終保留6個基本面因子，相應的評價指標如表4所示。保留1個月收益率反轉因子、12個月波動率因子和12個月換手率因子，如表5所示。保留7個利用遺傳算法構建的因子特征，如表6所示。

表1 待檢測的基本面因子及其計算方式

表2 待檢測的量價因子及其計算方式

表3 遺傳算法的相關參數

表4 保留的基本面因子及評價指標

表5 保留的收益率反轉、波動率和換手率因子

表6 遺傳算法挖掘的量價特征

六、多因子模型的構建

為了驗證集成學習算法在多因子模型問題上的有效性，本節將以上一章篩選出的16個因子作為特征，分別使用隨機森林、Adaboost和XGboost等算法進行滾動訓練，實現對股票未來漲跌狀態的預測。同時，將模型與同期的指數和傳統打分法進行對比，說明策略的有效性。具體步驟是：

第一，提取數據。從天軟數據庫提取中證800歷史成分股的相關數據，數據區間為2010年1月-2020年1月。需要說明的是，這里要對股票池進行動態調整，保證調倉日的股票池與中證800當天的成分股一致。

第二，特征和標簽的構建。以16個候選因子作為特征，并對特征進行預處理。預處理方法包括中位數法去極值和行業內標準化。計算個股未來20個交易日的收益率，排名前30%的股票作為正例，標簽為1，排名后30%的股票作為負例，標簽為0。這樣每只股票就作為一個樣本，樣本的標簽是1或0，特征是該股票在當前時刻的因子暴露為維的向量。

第三，模型的訓練。采用滾動訓練的方法進行模型訓練，訓練集長度為12個月，測試集長度為3個月。

第四，模型的評價。以AUC和策略的回測表現作為模型的評價指標。進行回測時，根據模型在測試集的預測進行調倉，調倉頻率為月頻，每個調倉日選取預測值最高的50只股票構建投資組合，組合內按流通市值加權，手續費設置為雙邊千分之二。以中證800指數和等權打分法作為比較基準。

(一)隨機森林算法

本小節展示隨機森林算法的建模結果。在進行訓練時，使用網格調參進行參數尋優，同時對輸入特征的重要程度進行了檢測，目的是剔除不重要的特征，降低過擬合風險。特征重要性以信息增益來度量，即計算各個特征在每棵子樹中提供的信息增益的平均值，信息增益的均值越高，特征的重要程度越高。16個候選因子的重要程度如表7所示。總體來看，各個特征的重要程度分布比較平均，不存在重要性特別低的特征，說明第3章構建的因子特征能夠提供比較明顯的信息增益，無須進行剔除。

表7 因子重要程度

隨機森林算法測試集的AUC表現如圖1所示。AUC的均值達到0.577，除個別月份外，AUC值均保持在0.5分界線的上方，分類的準確率和穩定性較好。模型測試集的回測表現如圖2所示。2011年至今，隨機森林模型的年化收益率達到20.817%，而等權打分法和中證800指數的年化收益率分別為13.173%和4.23%，具體的評價指標如表8所示。為評價隨機森林策略的穩定性，本文進行了分年度回測，隨機森林、等權組合和中證800指數各年份的收益率如表9所示。隨機森林策略僅在2015年和2018年小幅跑輸等權打分法，其余年份均明顯占優，說明相比于等權打分法，隨機森林策略具有明顯的優勢。與中證800指數相比，隨機森林策略各年份的超額收益也比較穩定，僅在2020年一月份小幅跑輸指數，其余年份均明顯優于指數。

圖1 隨機森林測試集AUC變化

圖2 隨機森林策略凈值變化

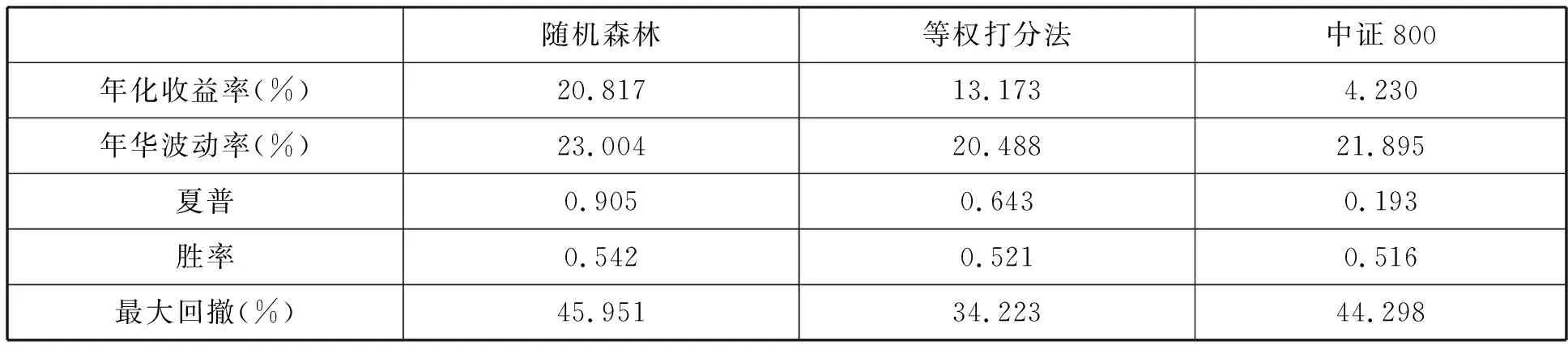
表8 隨機森林、等權打分法和中證800表現對比

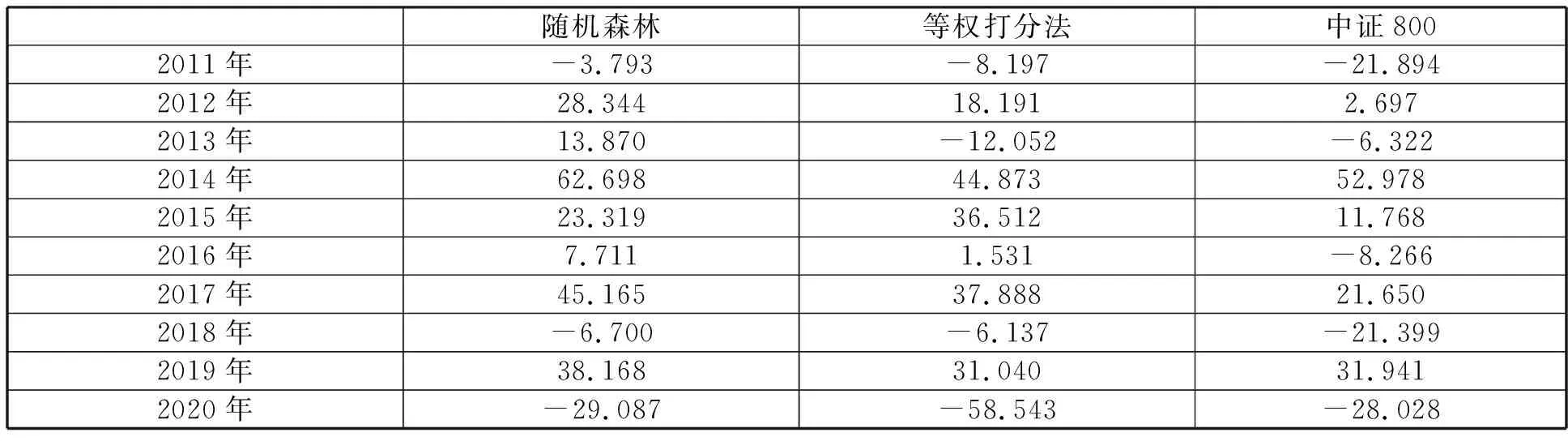
表9 隨機森林、等權打分法和中證800分年度表現對比

(二)Adaboost算法

本小節展示使用Adaboost算法的建模結果。進行模型訓練時，使用了網格調參對基學習器的個數(n_estimators)和學習率(learning_rate)兩個參數進行調優。基學習器的個數和學習率是boosting框架下的重要超參數，這兩個參數通常應該結合來看。基學習器的個數決定了迭代的次數，而學習率決定了每次梯度下降所取得“步長”，所以這兩個超參數共同決定了損失函數能否收斂至局部最小值以及以何種方式收斂至最小值。基學習器的個數較大時，如果學習率較小，會導致收斂速度較慢，如果學習率較大，可能導致損失函數在最小值附近反復跳躍，或無法收斂至最小。基學習器數量較少時，如果學習率較低，可能導致在距離最小值較遠的地方停止，如果學習率較大，同樣會導致梯度反復跳躍的情況出現。所以選擇合適的基學習器個數與學習率顯得尤為重要。

Adaboost算法測試集的AUC表現如圖3所示。AUC的均值為0.570。采用與隨機森林策略相同的方法對Adaboost策略進行回測，繪制的累計凈值曲線如圖4所示，并計算評價指標如表10所示。發現Adaboost策略的表現明顯優于等權打分法，等權打分法的年化收益率為13.173%，而Adaboost的年化收益率達到了22.096%。從分年度結果來看，如表11，Adaboost策略僅在2012年小幅跑輸等權打分法，其余年份均明顯占優。在與中證800指數的對比中，Adaboost策略的表現同樣亮眼，每年都戰勝了同期的指數。

圖3 Adaboost測試集AUC變化

圖4 Adaboost策略凈值變化

表10 Adaboost、等權打分法和中證800表現對比

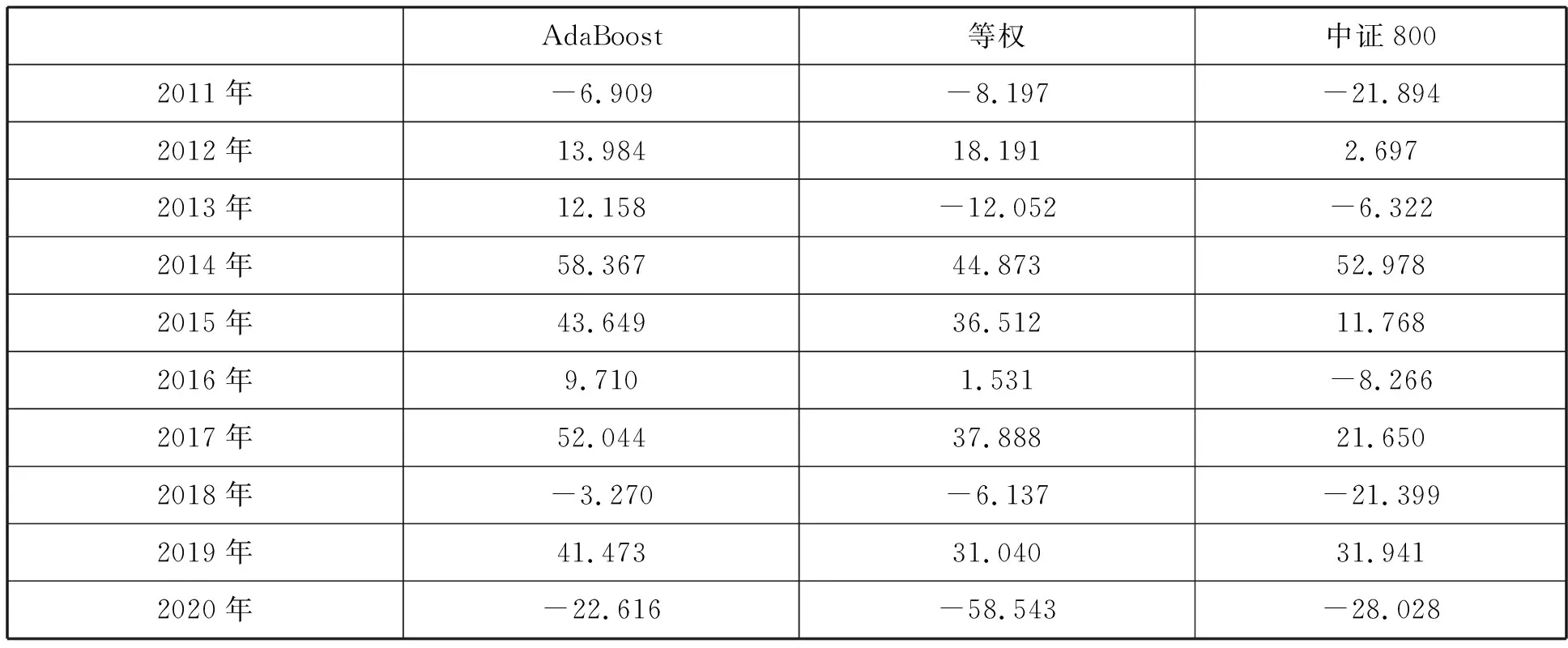
表11 Adaboost、等權打分法和中證800分年度表現對比

(三)XGBoost算法

XGboost在訓練基學習器時借鑒了隨機森林的思想，可以對樹的最大深度進行設置，降低過擬合風險。本文滾動訓練XGboost模型時，對基學習器個數、學習率和樹的深度進行了尋優，其余參數使用默認值。模型測試集的AUC表現如圖5所示。AUC的均值為0.573。模型累計凈值曲線、評價指標和分年度表現如圖6、表12和表13所示。XGboost策略的年化收益率為18.986%，低于隨機森林和Adaboost，但仍然優于等權打分法和中證800指數。XGboost在2019年和2020年1月的表現不如等權打分法，其余年份表現尚可。在與指數的對比中，XGboost在2013年、2014年和2019年小幅跑輸指數，2020年1月份大幅落后于指數，其余年份戰勝了指數。總的來看，XGboost策略在2019年后表現平平。

圖5 XGBoost測試集AUC變化

表13 XGboost、等權打分法和中證800分年度表現對比

(四)模型組合

從上述實證結果來看，將多因子選股當作分類問題來處理，使用分類算法滾動訓練模型取得了不錯的效果。如表4-8所示，隨機森林和Adaboost的回測效果比較出色，年化收益率分別達到了20.817%和22.096%，夏普比率分別為0.905和0.957。XGboost的效果稍遜，年化收益率18.986%，夏普比率為0.828，但還是在大部分年份戰勝了等權打分法和中證800指數。說明在因子相同的條件下，采用機器學習算法來構建多因子策略要優于等權打分法。

對于表現較好的兩個模型——隨機森林和Adaboost，可以按照一定的方式進行復合，以進一步提高模型的表現。本文采用軟投票的方式對隨機森林和Adaboost進行了組合，即將隨機森林預測樣本類別為1的概率與Adaboost預測樣本類別為1的概率取平均，作為最終的預測結果，每次仍然取預測類別為1的概率最高的50只股票進行建倉。采用這種軟投票的方法進行模型組合的回測表現如表14所示，累計凈值曲線如圖7所示。可見，通過模型組合，獲得了比單一模型更好的收益表現，年化收益率提高到22.697%，夏普比率提高到0.987。

表14 不同模型表現對比

圖7 組合策略的凈值變化

七、結論與展望

本文將多因子選股當作分類問題處理，使用隨機森林、Adaboost、XGboost等集成學習算法進行滾動訓練，實現對股票未來漲跌狀態的預測，并對模型在測試集的AUC和投資表現進行了回測。發現在使用的因子相同時，使用集成學習算法進行滾動訓練獲得了比等權打分法更好的年化收益率和夏普比率，而且在每年均戰勝了基準指數。

本文的研究過程主要分為兩個步驟。首先進行了單個因子的構建，包括基本面因子和量價因子。在進行構造量價因子時，使用了遺傳算法，增加了因子的多樣性。本文以信息比率和累計IC為標準，最終保留16個因子來構建多因子模型。其次，本文使用了3種常見的集成學習算法滾動地訓練分類模型，訓練集和測試集的長度分別為12個月和3個月。對模型在測試集上的投資效果進行回測，發現使用集成學習算法進行滾動訓練的效果明顯優于等權打分法和中證800指數，其中隨機森林和Adaboost的表現更優，夏普比率分別達到0.905和0.957。最后，對于表現較好的兩個模型——隨機森林和Adaboost，使用軟投票的方法對模型進行組合，實現了對原有模型的增強，新模型的夏普比率提高到0.987。

通過實證檢驗，本文證明了使用集成學習算法來構建分類器，可以獲得比傳統的多因子打分法更好的效果，且在2011—2019年每年均戰勝了基準指數，表現比較穩定，適合指數增強型基金產品。在實際投資中，指數增強型基金的目標是提供高于標的指數的收益，本文的股票池設置為中證800指數的成分股，根據模型預測結果按月調倉，在回測區間內，每年均戰勝了中證800指數，超額收益相對穩定，為指數增強產品提供了一種新思路。