小學數學錯題分析及應用研究

王科崢

摘要：文章對小學一至六年級中的68個策略性知識典型錯題的錯因進行分析，其因有受身心發展制約，未發現新舊情境中的細微差異導致錯誤;由于認知結構的缺陷，導致解題策略的錯誤推廣;學生對解讀問題中的一些特殊要求存在困難，導致解題策略錯誤;概念圖式不夠豐富，導致解決應用策略的錯誤。通過實踐提出三個干預策略：提前干預策略;過程性干預策略;錯誤發生后的干預策略。

關鍵詞：小學數學;策略性知識;典型錯題;錯因分析;干預策略

如何合理、系統地利用“錯誤資源”，達到輕負高質的效果？這需要進一步深入研究。筆者收集了小學數學一至六年共298個典型錯題。按錯題的知識屬性分為陳述性知識、程序性知識和策略性知識三類。其中屬于策略性知識典型錯題有68個。本文對68個錯題的錯因進行專項分析，在實踐的基礎上提出了三個有效的干預策略。

一、策略性知識典型錯題的原因分析

“典型錯題”，指學生解數學題時，在口答、書面等練習中呈現出的錯誤率較高（全班的錯誤率≥15%）的數學題，如果錯題的知識屬性是屬于策略性知識，筆者把這樣的錯題定義為策略性典型錯題。

（一）受身心發展制約，未發現新舊情境中的結構性中細微差異導致錯誤

[案例一]我的前面有9人，后面有5人，一共有多少人？學生的錯誤解答為9+15= 14，錯誤率為57.7%。

師：你認為這樣做對嗎？

生：對的呀。

師：前面9人包括他嗎？后面呢？

生：不包括。

師：那說明9+5 =14人是錯的。錯在哪里呢？

生：沒有加進自己。

從訪談中看，對于9+5=14這種解題策略，學生還是堅持自己是正確的。說明學生掌握了求已知部分數+部分數=總數這個陳述性知識，錯誤原因在于題中有3個部分數，而“我”這個部分數比其他兩個部分數更具有“隱性”因素，學生未能發現“新”的變化。

（二）由于認知結構的缺陷，導致解題策略的錯誤推廣

[案例二]A盒中有25個玻璃球，B盒中的玻璃球個數比A多15個，B盒中的玻璃球個數比C盒多18個，B盒中有多少個？C合中有多少個？學生的錯解出現在求C盒：40+ 18= 58（個），錯誤率為34.3%。

生：B盒中的玻璃球個數比A多。（指著）“多”

師：你是看到了“多”，就想到了加法，老師是這樣教你們的嗎？

生：（笑笑）不是，老師說什么大數，小數的。

師：那你為什么不用老師那個方法呢？

生：太麻煩了，這個容易。別人說過，后來我也想到了。

分析一個量比另一個量多（少），需要分析出大數、小數、相差數，然后找到相應的數量關系，即大數=小數+相差數，小數=大數一相差數，相差數=大數一小數。

（三）學生對認識題中的一些特殊要求存在困難，導致解題策略的錯誤

[案例三]從一張長36厘米，寬20厘米的長方形紙上剪下一個最大的正方形，求剩下部分圖形的周長是多少？學生錯解為（36+20）×2=112cm，

20×4=80cm.112 - 80= 32cm，錯誤率為34%。

生：我先算長方形周長，再算正方形周長，最后把兩個相減。

師：你是怎么想到可減的？

生：剩下的是周長啊。

“求剩下的量，用減法。”這是學生已多次應用且正確的觀念。由于周長計算的具有其特殊性，即“有限圖形周長的不可加（減）性。”對于這個知識的認識完全顛覆了學生對求“剩下量”的認識。

（四）由于概念圖式不夠豐富，缺乏聯系，導致解決應用策略的錯誤

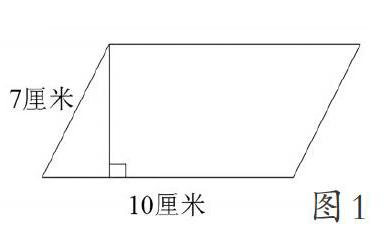
[案例四]如圖1，根據圖形，畫出距離是8厘米的高。錯誤率達84%。

生：題目里只說畫8厘米的高，沒有說要畫在哪條底上，我就按自己的習慣畫了這條。

師：畫好后，你想過這條高可能是8厘米嗎？

生：（低頭想，好一會兒），不對，應該是斜邊長一點。

師：你當時怎么沒想到呢？

生：這個（指了指左邊的三角形），我畫出來后就再也沒想。 從學生的訪談中看，解決此題的3個知識點，即直角三角形的斜邊大于任何一條直角邊、畫高的技能、平行四邊形有兩類高等，學生對此都明白的，技能也是掌握的。

二、策略性知識典型錯題在教學中的應用策略

（一）鋪墊性策略

鋪墊性策略，即有些錯誤是學生在新知識學習前，由于原有的知識結構“缺陷”、技能缺失等因素引起思考的錯誤，就要采用提前鋪墊，為學生奠定“正確想”的知識技能基礎。

1.加強陳述性知識和程序性知識的教學，夯實“正確想”的知識基礎

在策略性知識的了解階段，陳述性知識顯得尤為重要。在轉化階段，程序性知識又起到了重要的作用。要注重在操作程序中“夯實”陳述性知識概念。

如案例二，是因為學生原有認知里，知識結構出現了錯誤，即看到“多”就用“加”，看到“少”就用“減”。所以我們應該在新知教學前做好鋪墊。

首先建立正確的概念。題中的“多、少”與“加、減”運算沒有直接的邏輯推理關系。其次建立正確其程序。第一步，知道（ ）與（

）比;第二步，比的結果（

）多、（

）少;第三步，求（ ）;第四步，確定解決方法。

2.加強“數學表示”直觀能力培養，奠定“怎么想”的技術基礎

小學生正處于由形象具體思維向抽象邏輯思維的過渡階段，在問題解決中思維需要直觀的“數學表示”來支撐思考。這種能力要從低年級開始培養。具體有三個方面：首先培養圖示與文字的轉化能力;其次，培養“符號”表示的能力;最后重視圖示與條件間匹配的能力。

（二）“過程性”干預策略

過程性干預策略，即在新知識學習的發生、發展的過程中，正對新知識的特點，找到學生的思維可能出現障礙、阻隔的地方，引入相應的干預策略，突破難點，使學生頭腦中構建起“怎么想”的正確思路和方法。

1.用題組對比顯示新舊知識概念差異，減少出錯率

新舊知識在概念表述、題型結構、思考方法等具有某種相似性，這種相似性掩蓋了其差異，而概念差異可能是學生思維出現阻隔、障礙的“節點”。在教學中破解新舊知識的差異是干預的重點，其最常用策略是題組對比。

如案例三，學生受到原有知識經驗的負遷移，可以提供如下題組。

①甲比乙多5元，

②甲比乙多4/5元，

③甲比乙多4/5

通過對比，凸顯題①和題②都表示具體量。通過題②和題③的對比，重點突出③中4/5是“率”。

2.在解決多個概念融合的綜合題時需清晰概念，建立解決程序 一些策略性典型性錯題干預后仍有較高的錯誤率，如案例五。它在沒有干預教學之前的錯誤率為53.4%，在實行干預策略后，大樣本數據測查的錯誤還有33.3%，這就需要幫助學生清晰概念，建立關鍵程序。

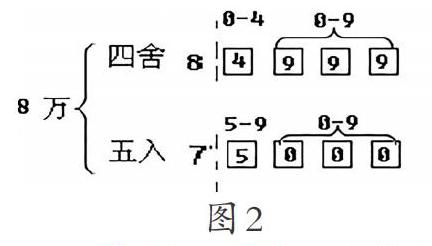
一個數省略萬后面的尾數是8萬，這個數最大是（

），最小是（ ）。

要解決這個題目要抓住3個關鍵。

（1）近似數是一個區間。用數軸的直觀形式理解“區間”。

（2）要清晰“最大”和“最小”兩個含義。

（3）要明確清晰可具體操作的程序。要配直觀圖示（如圖2）。首先，要判清楚“舍”與“進”的數位;其次，根據四舍五人中最大與最小的要排列出數字;最后，按照題目要求找到最大和最小的數。

（三）錯誤產生后的糾錯策略

1.發現錯因策略

策略性典型性錯題的錯因與陳述性、程序性知識屬性錯題的錯因相比，相對而言更為復雜，更為隱性。錯誤要關注兩點：第一，“他（我）原來是怎么想的？”第二，“他（我）錯在哪兒？”

（1）通過“說”“寫”等方式，認識“他（我）原來是怎么想的”

當錯誤出現后應尋找它的源頭，即思考的過程。思考過程具有隱性化。把它顯性化的策略說和寫。讓學生通過“聲音”表達自己的想，高年級的學生也可通過“寫”（思考思路、思考依據）的方式表達自己是怎么想的。

（2）通過正確與錯誤的方法對比，認識“他（我）錯在哪兒”

錯誤思維方式往往帶有一定的隱蔽性和頑固性。僅靠教師的正面示范，讓學生認識到錯，改變原來的思維方法，效率會比較低。 2.矯正錯誤策略 矯正錯誤更重要的是矯正錯誤的思考方式和思考方法。它僅僅靠訂正一個錯誤的題目難以實現，需要在多種變式練習中完成。提供非概念變式練習題，凸顯出變中不變，及時鞏固正確的想法;還可以提供概念變式練習題，在這些變式題中的練習中，凸顯出變與不變的應對方式，以達到融會貫通。

（1）提供非概念變式題，及時鞏固

提供相同類型的習題，讓學生在解決這些習題中不斷強化正確的思考方式，以此弱化原有的思考方法。在這個過程中，不是以正確的解答為主要目的，而是改變思考方法為主，具體的方式，讓學生通過寫、畫、說等多種不同的方式來表達正確的思考方法。要增加與原題目的對比，凸顯出不變的方法。

（2）提供概念變式題，融會貫通

提供變式習題，這既能鞏固原有正確的思考方法，又能達到舉一反三、觸類旁通的作用。在這個過程中也要與原題的對比，凸顯出變化的地方及改變相應的思考方法。

參考文獻

[1]宋乃慶，朱德全.論數學策略性知識的學習[1]數學教育學報，2000（02）.

[2]曾茂林，羅剛.對策略性知識的理解及教學初探[J]宜賓學院學報，2001（04）.

[3]湯春燕，趙國明.小學數學一至六年級典型錯題資源庫的建設與應用[J].浙江教學研究，2013（03）.