一種故障干擾解耦的航天器主動容錯控制方法

宗 群，楊希成，張秀云，劉文靜

(1.天津大學 電氣自動化與信息工程學院, 天津 300072； 2.空間智能控制技術重點實驗室(北京控制工程研究所), 北京100190)

隨著世界經濟的不斷發展，作為當今科學技術中發展最快的尖端技術之一，航天科技得到了越來越多國家的高度重視，發揮著愈加重要的作用. 由于航天任務復雜程度日益增加，對火箭、衛星等航天器的可靠性提出了更高的要求. 為確保航天器的安全性、可靠性及航天任務的順利進行，深入開展航天器故障診斷與容錯控制技術具有重要的理論研究意義與實際應用價值.

近年來，國內外學者針對故障診斷與容錯控制方面進行了廣泛研究. 2007年英國埃克塞特大學的Edwards等[1]針對不確定非線性系統設計滑模觀測器進行故障檢測并采用等效輸出注入的方法估計出故障信息. 2010年加拿大溫莎大學Mehrdad Saif等[2]針對一系列不確定動態系統，提出一種二階滑模觀測器進行故障診斷. 2012年韓國蔚山大學Mien Van等[3]研究了機械臂的魯棒故障檢測算法，解決了傳統的利用等價輸入注入重構故障時需要引入濾波器的問題，設計三階滑模觀測器實現故障的重構，但未考慮不確定及干擾影響. 2012年意大利帕維亞大學Capisani等[4]針對機械臂執行器與傳感器故障問題，采用高階滑模觀測器實現執行器故障估計. 2012年韓國學者Dong-Jae Lee等[5]提出了一種同時估計不確定系統狀態和擾動的魯棒H滑模廣義觀測器，并采用滑模策略對輸入故障進行重構，但未能實現故障和干擾的完全解耦估計. 2014年哈爾濱工業大學劉建興等[6]針對非線性不確定系統，提出一種基于觀測器的故障重構策略. 通過多次坐標變換，將不確定及故障分別解耦在不同的子系統，并利用自適應增益二階滑模觀測器來觀測系統狀態. 2015年南京航空航天大學姜斌等[7]針對存在干擾不確定以及驅動器故障下的四旋翼無人機系統提出了一種魯棒滑模反步控制器. 2015年法國波爾多大學De Loza等[8]針對帶有故障的線性系統，無需故障檢測與隔離，設計連續容錯控制分配，首次提出基于固定控制分配的連續積分滑模，利用高階滑模觀測器估計狀態，避免了抖振，估計了故障. 2016年韓國蔚山大學Mien Van等[9]考慮了不確定影響，建立超螺旋觀測器同時估計系統狀態和故障信息. 2016年英國埃克塞特大學Edwards等[10]研究了如何在干擾存在條件下提高自適應觀測器的性能，提出一種滑模自適應觀測器. 2017年哈爾濱工業大學羅文生等[11]提出一種非線性觀測器的故障診斷方法, 利用一種改進的超螺旋進行觀測器設計, 這種觀測器不僅可以估計狀態，還可以估計故障信息. 2017年西北工業大學穆凌霞等[12]將H性能指標引入到觀測器設計中,從而抑制不確定性和輸出擾動對狀態估計的影響，但此方法未能完全消除不確定和擾動帶來的影響. 2018年北京航空航天大學胡慶雷等[13]針對執行器故障、外部干擾和輸入飽和同時存在情況下的航天器系統，提出了一種包含符號函數的迭代學習觀測器，降低了計算復雜度, 在魯棒控制分配策略中引入故障估計信息，提高了容錯能力. 2019年伊朗阿米爾卡比爾大學Nemati等[14]考慮模型的不確定性、輸入和環境干擾，針對衛星編隊飛行的故障診斷問題，設計了一組非線性魯棒未知輸入觀測器，可以對未知輸入干擾進行解耦，減弱模型不確定和外部干擾的影響，但同樣未能實現完全解耦.

綜上所述，傳統的故障診斷方法首先檢測故障發生，并設計故障估計器對故障大小進行估計，進而利用故障估計值進行容錯控制器設計，從而保證故障發生后系統的穩定性. 但這種處理方法在完成故障估計后，干擾則需進一步通過自適應或觀測器等手段解決，這會增加系統計算量，且帶來一定的時間延遲. 相關學者對此展開了一系列研究，但都未能完全消除干擾帶來的影響.

因此，針對以上問題，本文對干擾及故障影響下的航天器姿態控制系統，首先通過設計未知輸入觀測器進行故障檢測及估計一體化設計，實現干擾影響下對系統狀態和故障的有效估計；在此基礎上，考慮到此方法中故障必須可導需求，進一步考慮傳感器測量誤差，設計新型的自適應滑模未知輸入觀測器，減小干擾處理帶來的時間延遲，同時實現對故障及干擾的解耦估計，并設計多變量終端滑模容錯控制器，保證航天器控制性能的快速恢復.

1 航天器姿態控制模型建立

為建立航天器姿態模型，首先給出地心慣性坐標系及機體坐標系的定義如下.

地心慣性坐標系：所有的運動都要參照地球慣性坐標系，記為OIXIYIZI. 地球慣性坐標系的坐標原點OI為地球中心，以赤道面為基準面，OIXI軸沿地球赤道面與黃道面的交線，并指向春分點，OIZI軸指向北極方向，OIYI軸在赤道面內與OIXI軸和OIZI軸構成右手坐標系.

機體坐標系：記為OBXBYBZB，本體坐標系與航天器本身連接在一起，與航天器的主慣量軸一致，航天器質心為其坐標原點OB，滾動軸為OBXB軸，俯仰軸為OBYB軸，偏航軸為OBZB軸，滿足右手系準則.

基于上述坐標系，建立航天器姿態動力學模型：

(1)

式中：ω=[ωx,ωy,ωz]T為航天器角速度；J為轉動慣量,J=diag[Jx,Jy,Jz]，其中Jx、Jy、Jz為航天器主慣量軸；Tu為系統控制力矩，Tu=[Tux,Tuy,Tuz]T；Td為系統干擾力矩,Td=[Tdx,Tdy,Tdz]T.

航天器運動學模型表達形式為

(2)

式中φ、θ、ψ分別為滾轉角、俯仰角及偏航角.

考慮較小的航天器姿態偏差，以及低軌運行航天器所受到的干擾力矩主要為重力梯度力矩，上述航天器模型、可轉化為

(3)

式中p=[φ,θ,ψ]T為姿態角，其余變量表達形式為

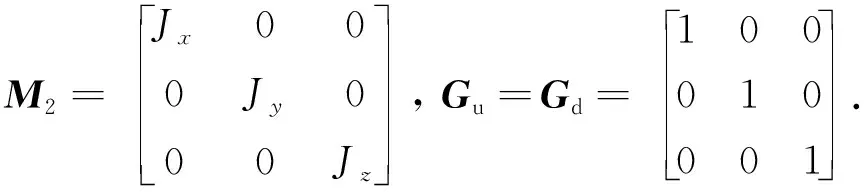
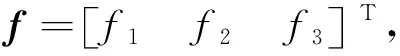
(4)

2 干擾影響下的故障估計器設計

針對航天器線性化模型，考慮干擾d及故障f影響，通過將故障f擴展為系統狀態量，獲得擴展狀態系統，并設計未知輸入觀測器，保證干擾影響下對擴展狀態的有效估計，從而實現故障檢測及估計一體化設計.

(5)

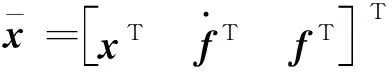
基于航天器擴展系統動態，設計未知輸入觀測器(unknown input observer, UIO)：

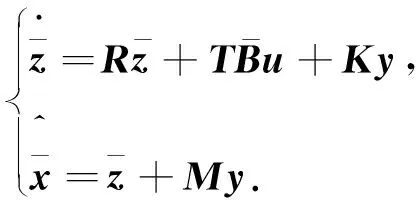
(6)

(7)

定義狀態估計誤差為

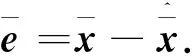
(8)

由式(5)、(6)可得

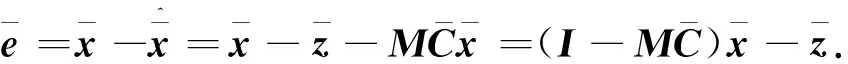
(9)

定理1針對航天器系統(5)，在假設1存在的條件下，設計如式(6)所示的未知輸入觀測器形式，如果存在正定矩陣P及Q，使得

(10)

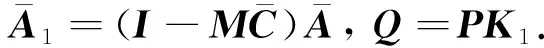
證明定義Lyapunov函數：

(11)

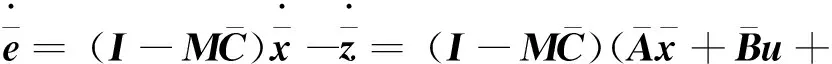
(12)

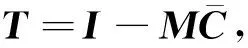
(13)

(14)

K2=RM.

(15)

那么，系統(12)可轉化為

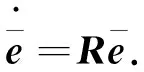
(16)

基于式(12)及式(16)，對Lyapunov函數(11)進行求導，可得

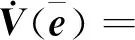
(17)

注1由于觀測器設計過程中相關參數過多，下面對式(10)及式(13)～(15)的參數選擇過程進行詳細說明：1)按照式(7)形式確定矩陣M；2)通過求解式(10)所示的線性矩陣不等式，獲得矩陣P及Q的取值，同時利用K1=P-1Q求得K1；3)基于式(13)～(15)，計算增益矩陣R、T、K2的取值.

3 干擾及故障同時解耦估計策略

上節觀測器(6)能夠實現對故障的有效估計，但無法對干擾進行同時處理，且此方法只能解決可導的故障類型. 因此，為解決以上問題，并進一步考慮傳感器測量誤差，本節針對航天器系統，設計自適應滑模未知輸入觀測器，避免先估計故障后處理干擾的時間延遲，且無需故障可導，同時實現對故障及干擾的解耦估計.

考慮傳感器測量誤差，航天器模型(4)可表示為

(18)

式中Bs∈R6×3為已知的系數矩陣.

假設2(A,C)是可觀測的，(A,B)是可控的.

假設3存在未知正數f0，滿足‖f‖≤f0. 干擾d是范數有界的.

3.1 自適應滑模未知輸入觀測器設計

通過將系統干擾擴展為系統狀態，基于線性化模型(18)，建立如下擴展系統模型：

(19)

設計如式(20)所示的自適應滑模未知輸入觀測器：

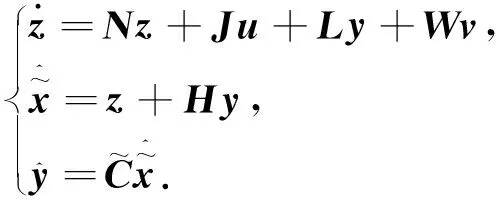
(20)

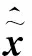
(21)

(22)

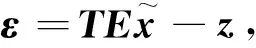
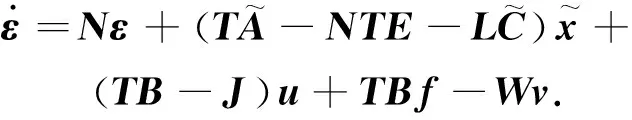
(23)

(24)

對估計誤差e進行求導，并設計參數滿足如下約束：

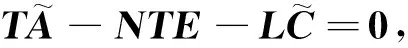
(25)

TB-J=0,

(26)

(27)

可以得到

(28)

(29)

由式(29)可知，若估計誤差e收斂至0，則故障f可由滑模項v求解獲得.

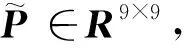
(30)

(31)

(32)

式中(·)+為矩陣的廣義逆，veq為等價輸出注入項.

證明下面將從兩步進行定理2的證明.

第1步擴展狀態估計.

設計Lyapunov函數：

(33)

(34)

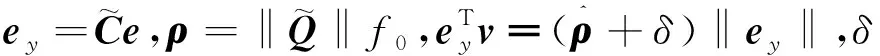
-ξ‖e‖2.

(35)

第2步故障估計.

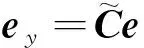
(36)

(37)

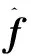
(38)

(39)

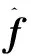
3.2 觀測器參數確定

首先，式(27)可以轉化為

(40)

(41)

式中Y1為任意正實數矩陣. 故矩陣T、H可分別表示為

T=T1-Y1T2,

(42)

H=H1-Y1H2.

(43)

因此，確定Y1即可確定T、H的取值.Y1的取值將在后面給出.

將式(27)代入式(25)可得

(44)

同理可得

N=N1-Y2N2,

(45)

(46)

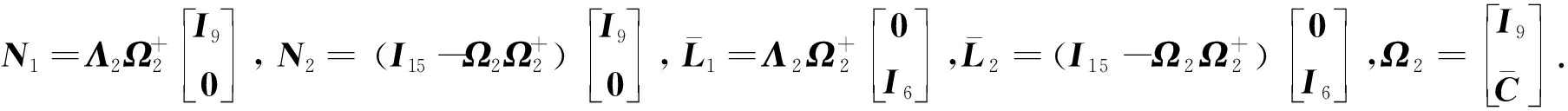
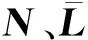
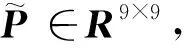
(47)

(48)

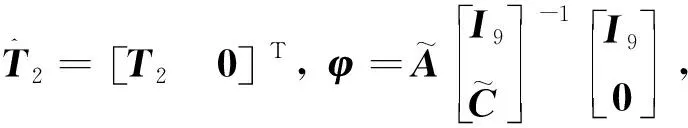
(49)

(50)

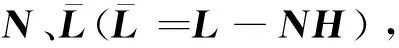
4 容錯控制器設計

(51)

其中D=Bded+Bfef為包含故障及干擾估計誤差在內的系統綜合不確定.

基于航天器姿態控制系統(51)，設計滑模面：

s=x1+λx2,

(52)

式中λ>0.

設計如下式所示的多變量終端滑模容錯控制器：

(53)

式中：k1>0，k2>0，r>0.

定理3[16]考慮航天器模型(18)，設計如式(53)所示的控制器，則存在正常數k1、k2、λ、r，使得狀態量x，即姿態角q會收斂至平衡點.

注2基于多時間尺度原理，容錯控制器及觀測器分別進行穩定性證明[17-18]，見定理1、定理2及定理3. 此外，在容錯控制器設計過程中進一步將觀測器估計誤差考慮在內，以提高系統性能.

5 仿真與分析

為了驗證所提出的航天器故障診斷與容錯控制設計的有效性，該部分將基于航天器模型進行仿真驗證分析. 其中，航天器的姿態角初值為

q(0)=[0.349 1 0.174 5 -0.261 8]Trad,

系統參數為

給定的外界干擾為

d=0.000 1×[sint,cost,sint]TN·m.

5.1 干擾影響下故障估計器設計仿真結果

本節中故障設計為

f3=0 N·m.

仿真結果如圖1～3所示. 圖1為故障估計及其對應的誤差圖，圖中藍色實線為故障真實值，紅色虛線為故障估計值，可以看出紅色虛線可以基本實現對故障真實值的估計，從而驗證了所設計的未知輸入觀測器的有效性. 故障估計誤差在較小范圍內波動，這種波動是由于故障之間的耦合相互影響造成的，屬于故障估計中的正常范圍. 圖2為狀態估計圖，圖中顯示航天器的狀態可以在有限時間內到達平衡點，且狀態估計值可以有效跟蹤真實值，從而驗證了所設計未知輸入觀測器的有效性.

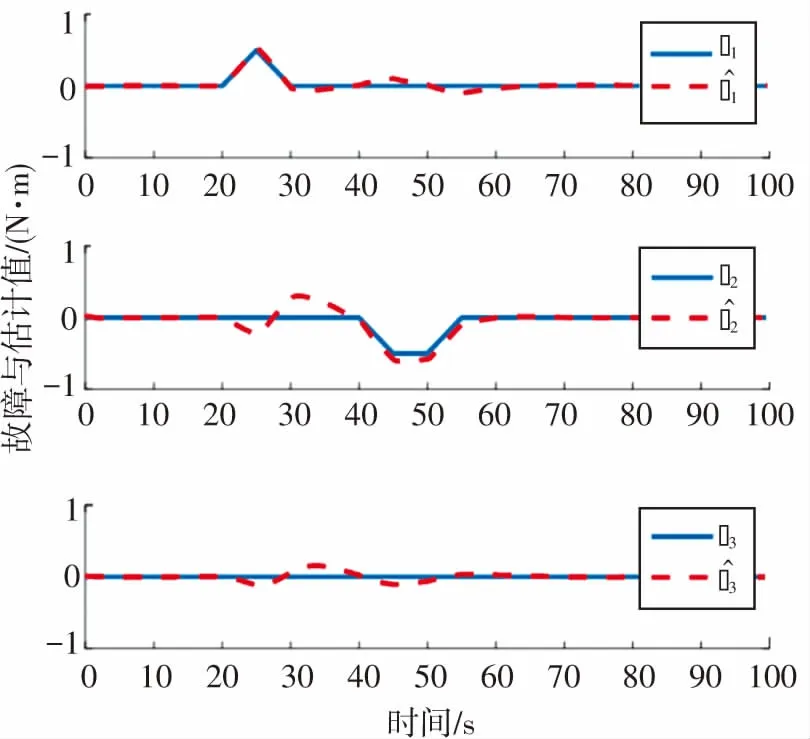
(a)故障估計圖-UIO

(b)故障估計誤差圖-UIO

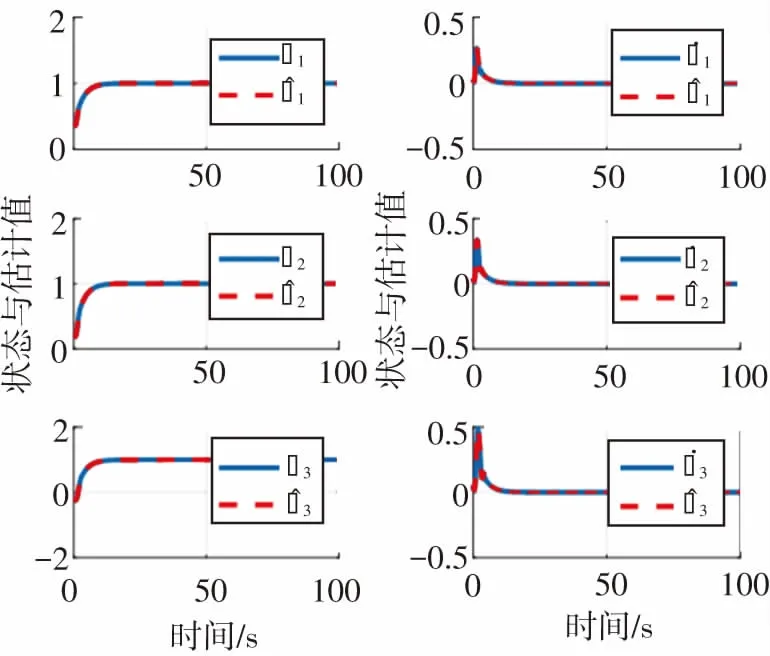
圖2 基于未知輸入觀測器的狀態估計圖

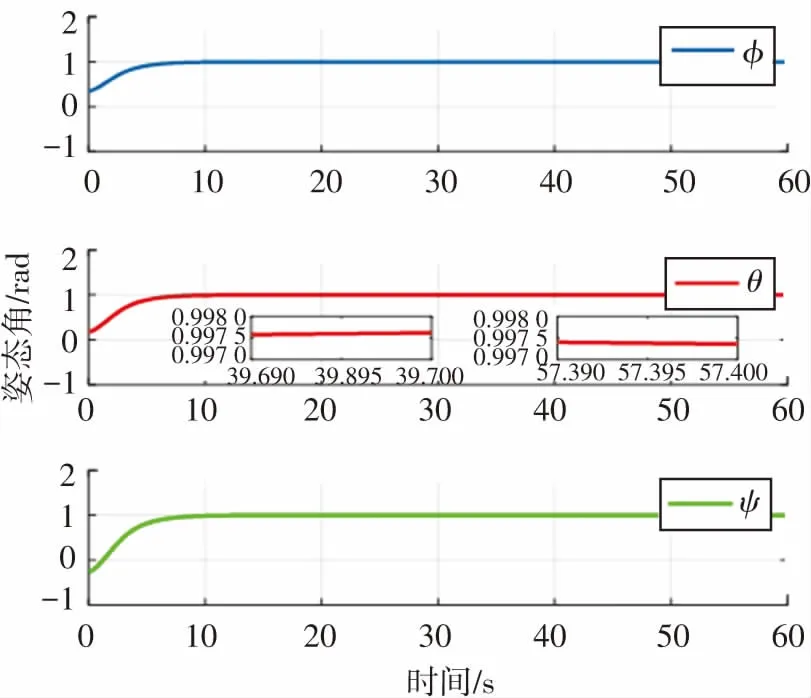
圖3為姿態角及姿態角速度的變化曲線圖，從圖中可以看出，在未知輸入觀測器-容錯控制器綜合作用下，航天器的姿態角及角速度可以在有限時間內到達平衡點. 未發生故障時觀測精度為1.9×10-3，而發生故障后在所設計的觀測器-容錯控制器綜合作用下，控制精度為2.2×10-3，系統控制性能較無故障時降低15.7%.

5.2 干擾及故障解耦估計仿真結果

本節中故障設計為

f1=0 N·m;

f2=0 N·m;

(a)姿態角變化曲線圖-UIO

(b)姿態角速度變化曲線圖-UIO

此外，自適應滑模未知輸入觀測器及容錯控制器參數設置見表1.

表1 自適應滑模未知輸入觀測器及控制器參數

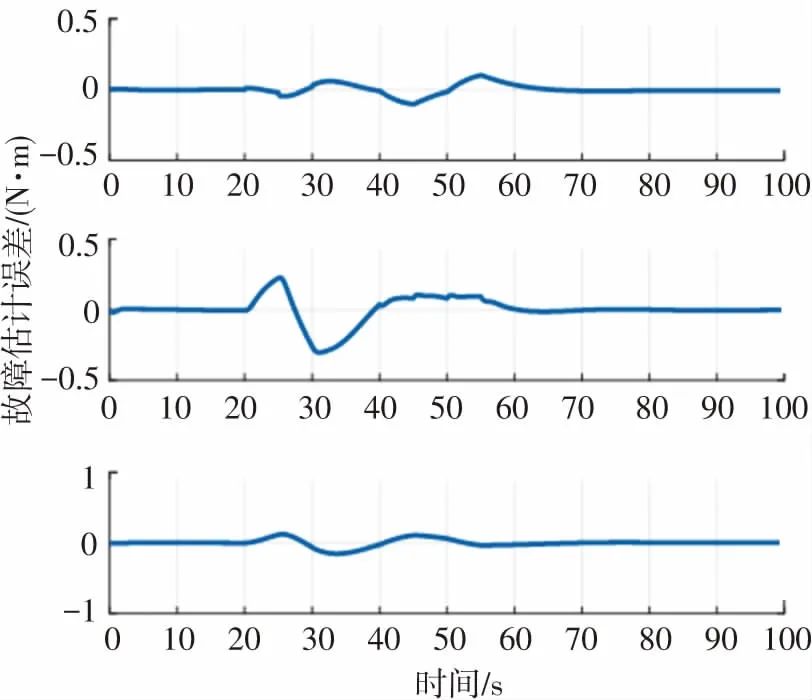
仿真結果如圖4～7所示. 圖4為所設計的等效輸出注入項對故障估計及其誤差圖，圖中故障估計誤差在零值左右浮動，所設計的觀測器可以基本實現對故障的估計；圖5為狀態估計圖，從圖中可以看出，估計曲線與實際曲線基本重合，所設計的觀測器可以實現對系統狀態的有效估計；圖6為干擾估計及其誤差圖，在開始時刻，干擾估計誤差會出現略微波動，但波動值很小并很快穩定，從而驗證了自適應滑模未知輸入觀測器對干擾估計的有效性. 圖7為姿態角及姿態角速度變化曲線，從圖中可以看出，基于所設計的自適應滑模未知輸入觀測器，實現對故障及干擾的有效估計后，設計的容錯控制器可以保證航天器的姿態角及角速度在有限時間內到達平衡點. 未發生故障時姿態控制精度為1.2×10-3，而發生故障后在所設計的觀測器-容錯控制器綜合作用下，控制精度為1.3×10-3，控制性能較無故障時降低8.3%.

(a)故障估計圖-ASUIO

(b)故障估計誤差圖-ASUIO

圖5 基于自適應滑模未知輸入觀測器的狀態估計圖

(a)干擾估計圖-ASUIO

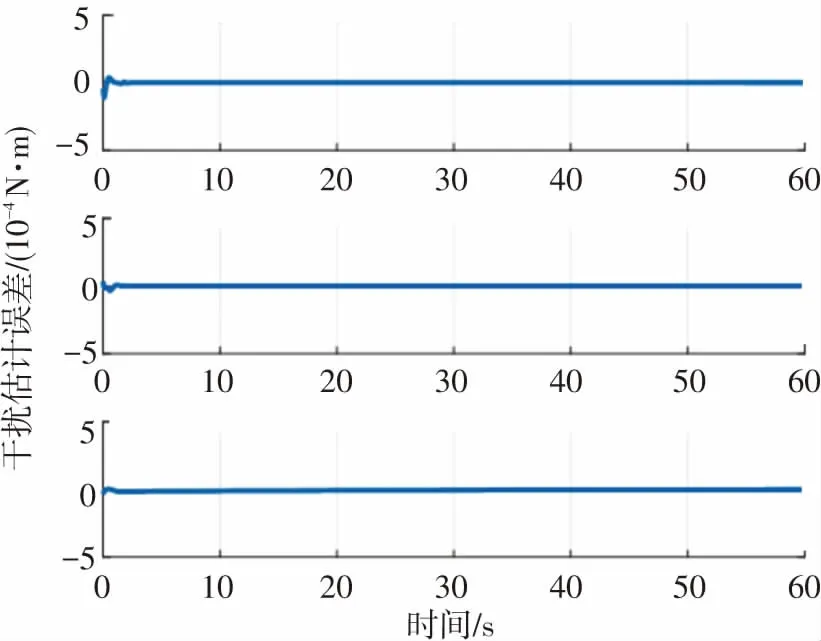
(b)干擾估計誤差圖-ASUIO

(a)姿態角變化曲線圖-ASUIO

(b)姿態角速度變化曲線圖-ASUIO

6 結 論

針對故障和干擾影響下的航天器線性系統，首先，基于擴展狀態系統設計基于未知輸入觀測器，進行故障檢測及故障估計一體化設計，實現了干擾影響下對系統狀態和故障的有效估計. 其次，基于等價輸出的概念，設計新型自適應滑模未知輸入觀測器，減小了干擾處理帶來的時間延遲，同時實現了對故障及干擾的解耦估計，且可以處理更廣泛的故障類型. 最后設計多變量終端滑模容錯控制器，提高了控制性能，保證了輸出跟蹤的魯棒性. 下一步考慮將所提出的方法進行擴展，以處理具有故障和擾動的非線性系統.