非線性間歇過程的迭代學習狀態估計

吳宏亮，趙忠蓋，劉 飛

(1.輕工過程先進控制教育部重點實驗室,江蘇 無錫 214122;2.江南大學 物自動化研究所，江蘇 無錫 214122)

0 引言

間歇過程是一類重復生產過程，按照相同的工序以批次為單位進行產品生產，越來越多地應用于食品、生物制藥以及化工領域。間歇過程中很多關鍵參數直接與產品質量相關，需要對其進行實時監測。但是，受限于傳感器技術的發展，間歇過程中的許多狀態變量難以測量或者測量成本很高，因此對間歇過程狀態變量的估計尤為重要，一直是工業界和學術界的關注焦點[1]。卡爾曼濾波(Kalman filter,KF)是一種廣泛應用的最優狀態估計的方法，但它適用于線性系統，而間歇過程通常具有非線性特性。對于非線性系統，通常采用擴展卡爾曼濾波(Extended Kalman filter,EKF)方法，無跡卡爾曼濾波和粒子濾波方法等[2-5]。但是，這些方法往往是連續過程狀態估計的簡單復制，忽略了批次之間的相關性。

近年來，為了提高間歇過程狀態估計的性能，迭代學習策略被引入狀態估計，考慮了批次運行之間的重復性和時間方向動態特性。迭代學習的思想來自于重復過程的控制，Arimoto等[6]提出一種迭代學習控制(iterative learning control,ILC)方法，針對重復運行的被控系統，通過前一次或前幾次的控制誤差信息修正當前操作的控制輸入，最終實現在整個時間區間上系統的輸出完全跟蹤上期望軌跡。基于迭代學習的思想，文獻[7-9]設計了確定性重復系統的迭代學習觀測器。然而，實際間歇生產存在噪聲干擾。

Zhao等[10]考慮包含隨機噪聲的非線性間歇過程，提出了一種用于批處理的迭代學習狀態估計算法，在當前批次粒子濾波的基礎上，引入上一批次輸出值的估計誤差作為修正項，包含了上一批次的信息，但修正項難以確定。Cao[11]等人提出了一種魯棒迭代學習卡爾曼濾波方法，用于狀態和輸出矩陣均具有范數有界不確定性的重復過程系統的狀態估計，但只給出了一種先驗類型估計。在文獻[12]中，提出了線性系統的迭代學習卡爾曼濾波器(Iterative learning Kalman filter,ILKF)，并在重復注塑機過程中進行了估計研究，驗證了ILKF在間歇過程中優越的估計性能。

但是，文獻[12]中的ILKF方法是一種線性狀態估計方法，而大多數間歇過程非線性嚴重。本文將基于標稱模型的擬線性化方法引入到間歇過程狀態估計中來，提出一種迭代學習擬線性卡爾曼濾波(Iterative learning quasilinear Kalman filter,ILQKF)方法。其中，標稱模型是間歇過程含噪聲模型的期望[13]，可以根據機理建模求得。考慮間歇過程正常運行下，每個時刻的狀態在標稱軌跡周邊變化，而狀態的變化呈現線性特征，因此ILQKF以實際狀態與標稱狀態之間的誤差為新狀態，首先基于標稱軌跡的擬線性化方法建立了與誤差相關的線性化模型；然后，應用ILKF方法對誤差模型進行狀態估計，而狀態軌跡等于誤差軌跡與標稱軌跡之和。ILQKF在狀態估計中充分利用了時間和批次雙維的特性，并消除了重復誤差。此外，相比ILKF方法，ILQKF還具有更寬松的初值條件。ILKF方法需要假設系統的初值滿足正態分布且均值為零，這在間歇過程中是一個不合理的假設，比如發酵過程的初始狀態可能是一個已知的非零量，如發酵過程中底物的初始濃度和發酵罐中的初值生物質濃度通常是一個給定的值，ILQKF方法更具有實用性。本文通過啤酒發酵例子驗證了ILQKF算法優越的性能。

1 迭代學習卡爾曼濾波

ILKF方法結合了KF和ILC的思想，充分利用了間歇過程的多批次重復性。

對于線性間歇過程系統模型(1)：

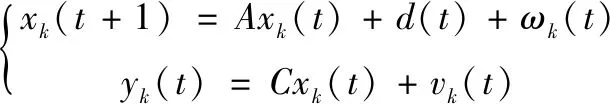
(1)

其中:k是系統的批次數，k∈[1,+∞)，t是采樣時間，t∈[0,M]，xk(t)∈Rn是第k批、第t時刻的狀態變量，yk(t)∈Rl是第k批、第t時刻的輸出變量，l≤n，d(t)是系統每批的重復干擾，為了設計ILKF，作以下假設[12]：

假設1：ωk(t)和vk(t)分別是獨立的雙維高斯過程噪聲和測量噪聲：

E[ωk(t)]=E[vk(t)]=0

E[ωi(j)vkT(t)] = 0

E[wi(j)wkT(t)] =Qδj,t;i,k

E[vi(j)vkT(t)] =Rδj,t;i,k

δj,t;i,k是雙維克羅內克函數，僅當j=t,i=k時，δj,t;i,k=I，否則δj,t;i,k=0。

假設2：d(t)為未知的有界重復干擾，隨時間變化。

假設3：初始條件xk(0)服從的獨立正態分布N(0,ζ)。

以上3個假設中,假設1與假設2相當于間歇生產過程中的兩種干擾，而假設3對初值的假設不符合絕大多數情況，本文第2節和第3節將給出合理解決假設3的方法。

定義δ為批次方向的后向差分算子：

δxk(t)=xk(t)-xk-1(t)

δyk(t)=yk(t)-yk-1(t)

(2)

同樣可以定義δxk(t),δyk(t),δωk(t),δvk(t)。

可以將系統改寫為兩個子系統，分別為時間方向上的子系統∑T和批次方向上的子系統∑B：

(3)

(4)

可以發現在∑B中，xk(t)與xk-1(t)之間的轉移矩陣是單位陣，即批次子模型∑B是個臨界穩定系統，可能會導致xk(t)的值不斷上升或震蕩，可以在原∑B子系統中加入系數τ<1，使系統穩定[12]：

(5)

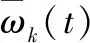
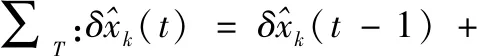
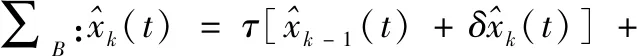
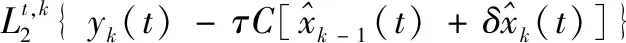
(6)

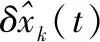
在間歇過程運行時，系統干擾分為重復干擾d(t)，隨機噪聲ωk(t)和vk(t)。通過把系統分解成時間方向和批次方向的子系統，并且設計子系統相應的估計器，抑制了隨機噪聲和重復干擾，并提高了間歇過程的估計精度。

圖1是ILKF雙向動態特性圖，其中橫軸Time代表時間方向，縱軸Batch代表批次方向，箭頭表示傳遞方向，此外在每個采樣時刻都有對應的測量值。橫軸上x的轉移只是隨著時間轉移，縱軸的x則通過批次方向的卡爾曼濾波進行更新，并且引入了矯正項δx，這個矯正項也可稱為學習項，它在時間方向上通過卡爾曼濾波進行更新。

圖1 ILKF雙向動態特性圖

2 非線性系統的擬線性化

2.1 動機

針對文獻[12]中的ILKF存在的非線性問題和不合理的初值假設等，本文將通過基于標稱軌跡的擬線性化方法將ILKF推廣到非線性間歇過程，并構造了一個誤差系統，通過對誤差系統的狀態估計來獲得系統的狀態估計，可以放寬初始值的假設。

考慮非線性間歇過程系統模型(7)：

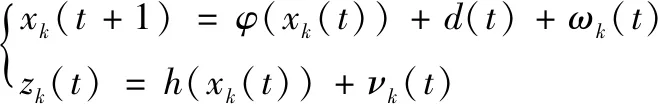
(7)

第1節中針對干擾的合理假設1和假設2在本節仍然成立；針對假設3，本節系統初值可以分布在任意均值的高斯分布中。

2.2 基于標稱軌跡的擬線性化方法

基于標稱軌跡的擬線性化方法對非線性模型(7)進行了線性化處理，在本節中，引入了一個誤差狀態系統，誤差系統的狀態為原系統狀態軌跡和標稱軌跡的偏差，通過估計誤差系統的狀態來得到非線性系統的狀態估計。由于存在干擾和噪聲，每批次運行所產生的狀態軌跡是不同的，但均是在標稱軌跡附近的波動[13]。

假設4：實際軌跡接近于標稱軌跡。

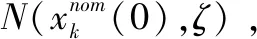
(8)

并且定義Δ為狀態的真實軌跡和標稱軌跡的誤差算子：

(9)

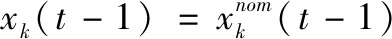
xk(t)=φ(xk(t-1))+d(t-1)+ωk(t-1)=

(10)

基于假設4，由(9)和(10)可得：

△xk(t)=Φ(t-1)△xk(t-1)+d(t-1)+ωk(t-1)

其中一階偏導近似系數為：

(11)

同理可得：

△zk(t)=Hk(t)△xk(t)+vk(t)

(12)

其中一階偏導近似系數Hk(t)為：

(13)

可以得到新的線性化系統：

(14)

Φ(t-1)和H(t)分別如式(11)和式(13)所示。

2.3 時間和批次方向的子系統

由式(2)中δ的定義易知：

δ△xk(t)=△xk(t)-△xk-1(t)

δ△zk(t)=△zk(t)-△zk-1(t)

工業生產中重復非線性過程一般每一批都是從相同的初始值開始，根據機理或者經驗模型，每一批都具有相同的標稱軌跡：

(15)

則根據式(2)和式(9)可得：

δxk(t)=xk(t)-xk-1(t)=△xk(t)-△xk-1(t)

即δxk(t)=δ△xk(t)，結合式(14)有遞推式：

δ△xk(t)=△xk(t)-△xk-1(t)=

Φ(t-1)δ△xk(t)+δωk(t-1)

同理：

δ△zk(t)=△zk(t)-△zk-1(t)=

H(t)δ△xk(t)+δvk(t)

參考式(3)～(4)將式(14)改寫成時間和批次兩個子系統，時間方向上的子系統∑T：

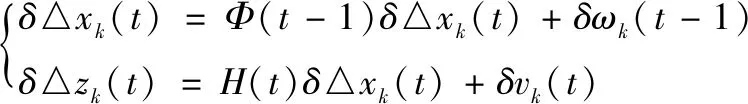
(16)

批次方向上的子系統∑B：

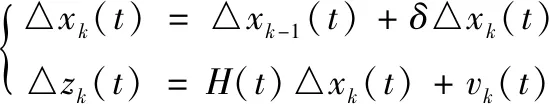
(17)

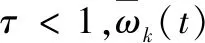
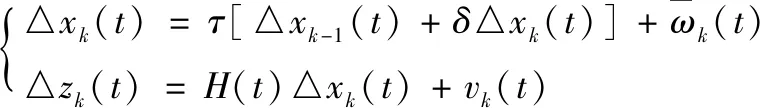
(18)

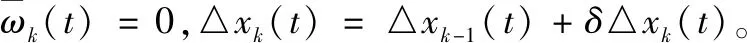
2.4 相關量的計算

本小節計算迭代學習卡爾曼濾波中需要用的量，相關噪聲協方差計算如下：

E[δωk(t)δωkT(t)] =

E[(ωk(t)-ωk-1(t))(ωk(t)-ωk-1(t))T] =

E[ωk(t)ωkT(t)] +E[ωk-1(t)ωkT(t)]=2Q

E[(ωk(t)-ωk-1(t))(ωk-1(t)-ωk-2(t))T]=

所以有：

定義:

由式(14)得：

(19)

(20)

3 迭代學習擬線性化卡爾曼濾波

本節針對非線性間歇過程的狀態估計問題，基于ILKF方法引入標稱軌跡擬線性化方法，提出了一種迭代學習擬線性化卡爾曼濾波(ILQKF)方法。ILQKF與已有的傳統狀態估計方法相比有以下三點的改進。

首先，與現有的非線性濾波方法比，現有的非線性濾波方法只考慮了時間方向的狀態轉移，而ILQKF參考ILKF的濾波框架可以利用之前所有批次的狀態信息，使得狀態估計誤差可以隨時間和批次兩個方向減小。

其次，與ILKF方法比，ILKF只針對線性系統，很難運用到非線性間歇生產過程上，而ILQKF引入擬線性化方法可以解決非線性問題，更適合運用到實際生產過程。

最后，與ILKF方法比，有著更為寬松的初始條件，在ILKF中，由于中間量的計算需要，文獻[12]給出了假設3，即原系統的狀態初值滿足0均值的正態分布。事實上，如果不滿足假設3，ILKF的遞推式將會變得極復雜，并且不為0的初值可能會使得批次子系統中的誤差協方差變大，從而降低濾波器的性能。然而，ILQKF不必滿足假設3，其依據在于擬線性化時引入了標稱模型作為中間變量。當系統初值滿足任意高斯分布，將高斯分布的均值作為標稱軌跡初值，則新狀態仍是0均值的正態分布，即ILQKF可以用于初值期望不為0的非線性系統的狀態估計。

3.1 ILQKF估計結構

與ILKF類似，基于ILQKF設計狀態估計器分為兩個階段：時間方向狀態估計和批次方向狀態估計。時間方向狀態估計包括對時間子系統ΣT的時間更新和測量更新；批次方向狀態估計包括對批次子系統ΣB的批次更新和測量更新。ILQKF的雙向動態特性與圖1不同點在于系統估計對象不是原系統狀態xk(t)，而是狀態與標稱軌跡的誤差Δxk(t)。

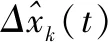
時間子系統ΣT的狀態估計器如下：

(21)

批次子系統∑B的狀態估計器如下：

(22)

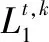
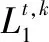
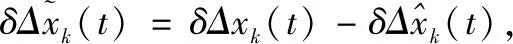
基于式(16)與式(21)得到∑T的估計誤差系統為：

(23)

基于式(18)與式(22)得到∑B的估計誤差系統為：

(24)

定義下列誤差協方差矩陣：

3.2 時間方向狀態估計

1)子系統∑T的時間更新：

(25)

(26)

2)子系統∑T的測量更新：

(27)

(28)

(29)

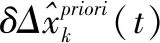
3.3 批次方向狀態估計

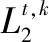
通過式(18)、式(22)，可得計算批次系統的估計誤差協方差Ck：

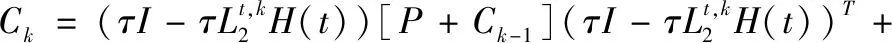
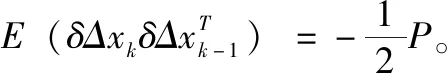
根據式(23)，式(24)和性質1，我們可以計算得到下面這些相關協方差：

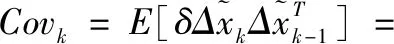
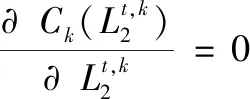
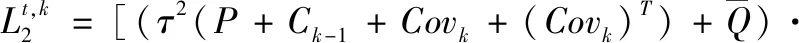
批次方向狀態估計流程：

1)子系統∑B的批次更新：

(30)

(31)

(32)

2)子系統∑B的測量更新：

(33)

(34)

(35)

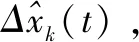
(36)

下面給出ILQKF算法：

算法開始：

輸入：φ(xk(t-1)),h(xk(t)),Q,R,zk(t),M,K；

循環開始，t=1：

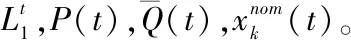
當t=M，循環結束，否則t=t+1。

濾波開始，k=1：

循環開始，t=1：

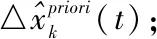
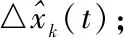
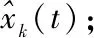
當t=M，循環結束，否則t=t+1；

當k=K，濾波結束，否則k=k+1；

算法結束。

4 啤酒發酵過程仿真

啤酒發酵過程是一種輸入為生物質(酵母)，基質(糖)和水，輸出為酒精，二氧化碳和水的間歇反應過程。發酵過程中，糖類和酵母的濃度都必須控制在合理的范圍之內[15]，因此十分有必要對啤酒發酵過程中的糖濃度和酵母濃度進行狀態估計。

將所提出的ILQKF方法應用到啤酒發酵過程的步驟如下：

步驟1：根據已有數據或者機理確定啤酒發酵的非線性標稱模型。

步驟2：初始批生產開始時，用EKF算法對糖濃度與酵母濃度進行估計。

步驟3：從第二批生產開始，以上一批的估計數據和標稱模型為基礎，用ILQKF算法進行估計，直到生產結束。

啤酒發酵過程中的糖濃度和酵母濃度的狀態空間模型[16]如下所示：

d(t-1)+ωSk(t-1)

Xk(t-1)+d(t-1)+ωXk(t-1)

zSk(t)=Sk(t)+vSk(t)

zXk(t)=Xk(t)+vXk(t)

其中:Sk(t)，Xk(t)，zSk(t)，zXk(t)，ωk(t)，vk(t)分別代表第k批次、第t時刻糖濃度，酵母菌絲的濃度，糖濃度的測量值，酵母菌濃度的測量值，過程噪聲，測量噪聲，ωk(t)和vk(t)相互獨立。d(t)表示每批只隨時間變化的重復性干擾，tc表示采樣間隔。模型參數如表1所示。

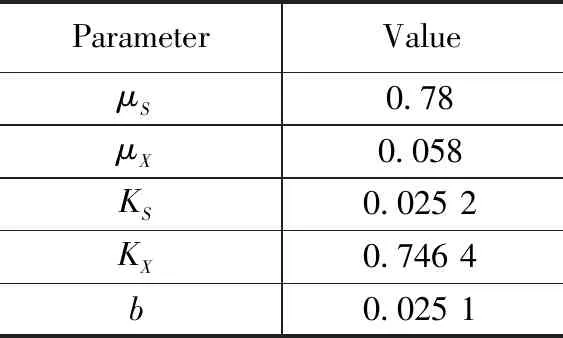
表1 模型參數表

設定步長為[0,3000]，初始值x(0)=xnom(0)=[S(0),X(0)]=[30;3]，白噪聲協方差矩陣Q=[0.00001,0;0,0.00001]，R=[0.25,0;0,0.0025]，設置τ=0.96，σ=10-12。

仿真時，初始批，即k=0批時，直接采用EKF進行狀態估計；從k=1批開始，將第0批由EKF得到的狀態估計值與標稱狀態之差作為ILQKF第1批的初始估計值，再采用ILQKF算法得到之后每一批的狀態估計值。

圖2顯示了啤酒發酵中基質(糖)和生物質(酵母)的狀態估計結果圖，實線代表實際值，虛線代表估計值。計算第20批基質濃度和生物質濃度平均估計誤差分別為0.082 203與0.017 091；計算第100批基質濃度和生物質濃度平均估計誤差分別為0.014 453與0.01 033。可以發現估計精度隨批次增加而增加。這是由于ILQKF建立了批次間的傳遞關系，可以過濾批次間的重復干擾，隨著批次的增加，濾波使用的信息越來越多，估計效果也越來越好。

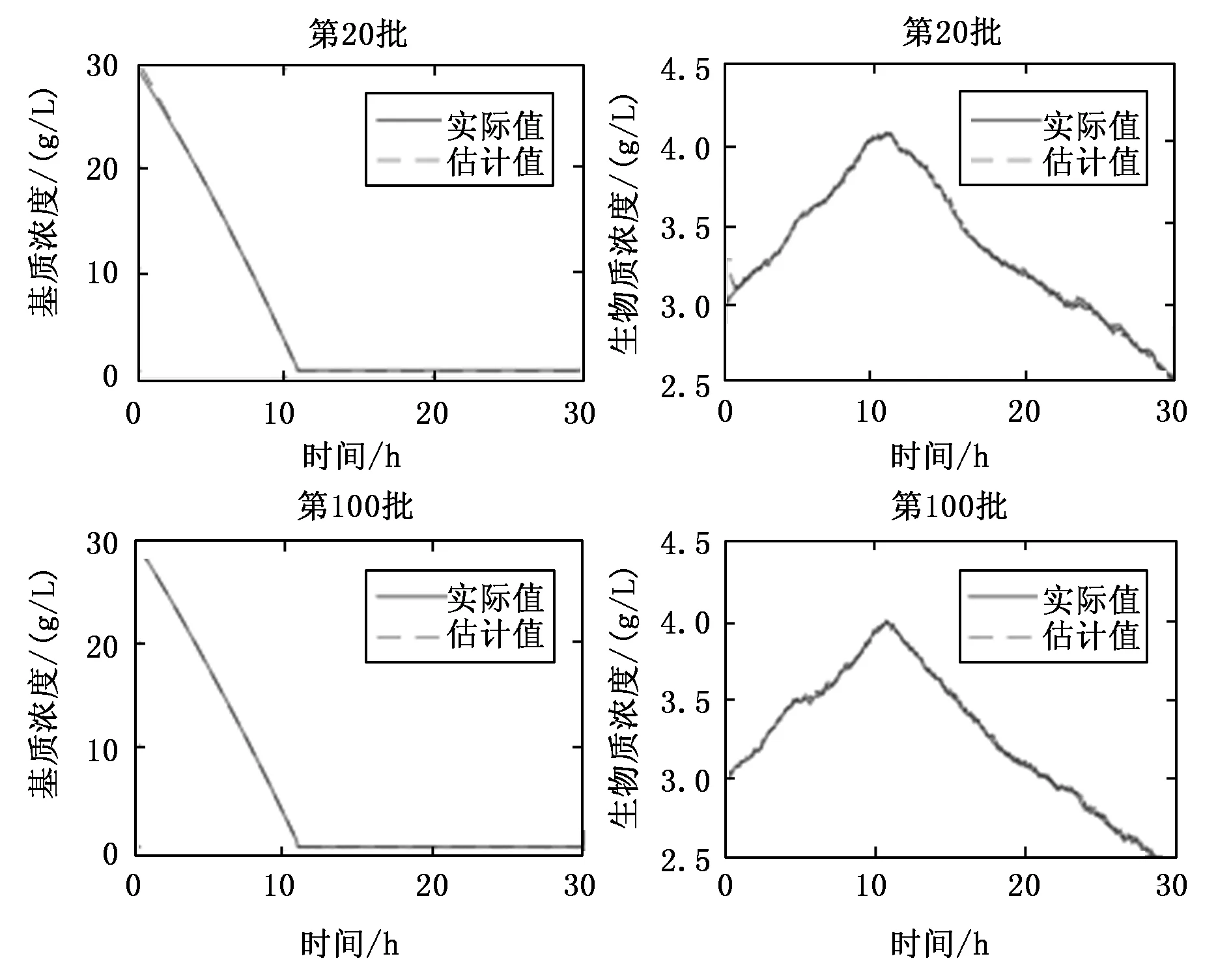
圖2 啤酒發酵狀態估計結果

圖3比較了EKF和ILQKF的狀態估計誤差。由于EKF估計對于每一批次都是獨立的，估計精度只依賴于初始值與動態噪聲的大小，隨著批次的增加，EKF的估計誤差沒有很大變化。而ILQKF可以利用上一批次的估計信息更新初始值減小初始誤差，還同時考慮了重復干擾與動態噪聲，隨著批次的增加，ILQKF狀態估計誤差逐漸收斂。圖3結果也表明ILQKF估計誤差隨批次遞減，而EKF估計誤差隨批次變化不大，所以ILQKF在多批次運行時的狀態估計效果明顯優于EKF。

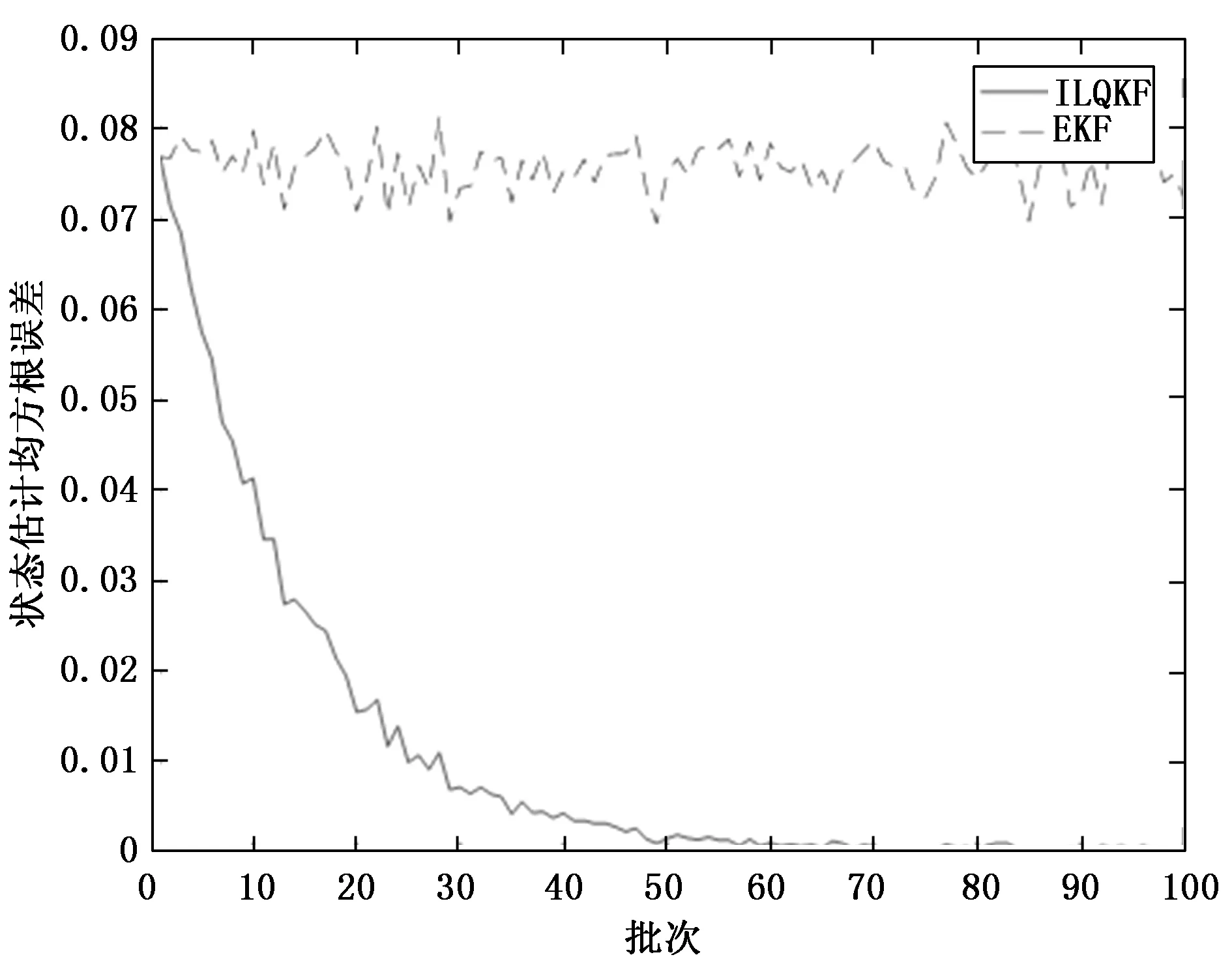
圖3 ILQKF和EKF的狀態估計誤差對比

5 結束語

本文基于迭代學習和標稱軌跡線性化的思想，設計了一種用于間歇過程的迭代學習擬線性化卡爾曼濾波器。該ILQKF方法將文獻[12]的ILKF方法擴展到非線性過程中，利用了間歇過程多個批次的信息，設計了時間方向和批次方向相應的卡爾曼濾波器，得到當前批次當前時刻的狀態估計值。啤酒發酵過程的仿真結果表明，狀態估計誤差隨批次的增加而減小直至收斂，相對于傳統的估計方法有一定的優勢。