基于ABC-SA混合算法的群控電梯優化調度

閆秀英，郭普靜，范凱興

(1.西安建筑科技大學 建筑設備科學與工程學院，西安 710055;2.西安建筑科技大學 建筑學院，西安 710055)

0 引言

隨著城鎮化進程的加快，電梯和電梯組的發展伴隨高層智能建筑的不斷發展而逐漸增加。電梯群控系統(elevator elevator group control system，EGCS)是根據建筑物內的交通流狀況，合理地分配多部電梯，根據管理目標、服務質量、服務數量及能量消耗的要求，電梯群控制器能合理、優化調度多部電梯以滿足服務目標要求[1]。建筑物中一組電梯的調度本質上是資源合理分配的組合優化。對于EGCS而言，尋找一種高效的調度優化算法能夠根據當前狀態決定調度某臺電梯響應某層呼梯信號至關重要。

以往群控電梯調度的研究主要集中在遺傳算法、模糊控制、神經網絡、最小等待時間法和專家系統等方法上。Beamurgia等人將遺傳算法應用于電梯調度問題，分析乘客的等待時間，電梯性能得到了改善但遺傳算法在搜索函數最優解時會花費較長時間[2]，王志華設計了基于模糊控制的群控電梯系統，但模糊控制缺少學習能力，難以實時調整模糊隸屬度函數[3]，神經網絡應用于電梯群控系統時訓練時間過長并且參數不易選擇[4]，專家系統不適合復雜多變的電梯系統，控制規則有限，適用于樓層較低的建筑物，最小等待時間法僅考慮了電梯的時間性能而忽略了現如今比較關注的其他能耗性能[5]。在節能時代，較好的EGCS應能滿足不同交通模式下的乘客需求，尤其是高峰交通模式。電梯群調度最大化節省時間的同時也應更加關注電梯節能調度，最大化地減少電梯群控系統的能耗并使時間性能保持在可接受范圍內。本文提出綜合考慮乘客乘梯及侯梯時間、減少系統能耗的優化思想進行群控電梯多目標優化。

在求解優化問題上，人工蜂群(artificial bee colony，ABC)算法具有參數設置簡單、易于實現的特點[6-7]。李彥蒼等人設計了引用信息熵的改進人工蜂群算法求解組合優化問題[8]，郎曼等人提出了采用人工蜂群算法對電梯群控進行節能優化[9]，王志剛等人應用ABC算法求解車輛路徑規劃問題[10]。人工蜂群算法盡管具有魯棒性強、計算簡單等優點，但仍存在收斂速度慢、易早熟等缺陷。

基于此，研究電梯群控優化調度時在基本人工蜂群的基礎上引入模擬退火(simulated annealing，SA)機制，以改善蜂群算法在迭代后期易于陷入局部最優而得到假象最優解的缺點，從而改善求解質量。并充分考慮影響電梯群控質量的關鍵因素，結合多目標優化思想建立多目標評價函數，利用ABC-SA混合算法對該目標函數進行求解，以得到更好的求解質量響應派梯策略，在節省乘客使用時間的同時節約系統能耗。

1 群控電梯多目標數學模型

1.1 優化目標

根據EGCS的隨機性，非線性特征以及乘客心理和生理上的需求，本文綜合考慮動態性能指標平均乘梯時間ART，平均侯梯時間AWT和系統運行能耗ANT，以實現電梯群調度的多目標優化。

1.1.1 乘梯時間評價函數

乘梯時間為tr電梯輸送乘客運行時間 和電梯在此過程中停靠時間ts之和，電梯停靠時間由乘客進出門時間tpa和電梯開關門時間toc組成。N為電梯內乘客總人數，RT(i,j) 為第i部電梯運行到第j層時電梯內乘客的乘梯時間，st為電梯群總臺數，sc為樓層數。平均乘梯時間ART如式(3)所示：

RT(i,j)=tr+ts

(1)

ts=toc+tpa

(2)

(3)

當正在輸送乘客時，期待隨著乘梯時間的增多，評價函數可信度降低，也就是評價值越高時，說明某一時刻電梯組時間性能良好，建立乘梯時間評價函數如式(4)所示。調度優化時希望所用時間越少越好，即隨著乘客乘梯時間的增長，乘梯時間評價函數逐漸減少并接近于0。

(4)

設乘梯時間為110 s時，此時乘梯時間評價函數值為0.000 1，則可根據乘梯時間函數求解評價函數的相關參數，即乘梯時間評價函數fr如下所示：

fr=e-0.00076RT2(i,j)

(5)

將公式(5)每20 s記錄一次fr評價函數值，由表1得出隨著乘梯時間RT(i,j)的增加乘梯時間評價函數fr逐漸減小。

表1 乘梯時間函數評價表

1.1.2 侯梯時間評價函數

侯梯時間定義為呼梯信號響應開始到電梯到達召喚層所用時間。侯梯時間評價函數與乘梯時間評價函數類似，不做具體說明。WT(i,j)為第i部電梯運行到第j層響應外呼信號所用的時間，候梯時間評價函數fw表達式如式(6)：

fw=e-0.0025WT2(i,j)

(6)

1.1.3 系統能耗評價函數

電梯系統的能耗包括啟停能耗和運行時的能耗。一般來說啟停能耗都要大于運行能耗，因此可通過減少電梯停靠次數來降低能耗。第i部電梯停靠次數記作n(i) ，系統能耗評價函數fn表達式為：

fn=e0.016n2(i)

(7)

1.2 建立多目標數學模型

電梯群控系統的優化屬于柔性多目標優化問題，能夠協調目標以使所有目標功能盡可能最佳地解決此類問題的關鍵。電梯群調度采用群智能多目標優化算法，綜合3個評價標準，采用加權組合法對3個指標進行加權求和，數學表達式如下：

F(x)=W1fw+W2fr+W3fn

(8)

式中,F(x)為多目標評價函數，評價函數值越大，評價派梯的可信度越高。fw、fr、fn分別為候梯時間評價函數、乘梯時間評價函數、系統能耗評價函數；W1、W2、W3為評價函數fw、fr、fn對應的系數權重，其中：

(9)

Wi體現了在不同交通模式下各評價指標的側重。當前電梯為上行或下行客流高峰時以減少乘客候梯時間和乘梯時間為主要目標，因此考慮適當增大fw、fr的權重系數W1、W2；同理電梯運行在層間或空閑交通模式下時以減少系統能耗為主，因此可增大fn的權重系數W3。

2 基于ABC-SA算法的電梯群控系統

2.1 ABC算法及SA算法的思想

人工蜂群(ABC)算法是一種模擬群體蜜蜂覓食特性的智能優化算法，該算法是土耳其學者Karaboga于2005年提出，通過模擬蜜蜂采蜜覓食的行為而尋找優化問題的解[11-13]。算法包括食物源(蜜源)、雇傭蜂(引領蜂)、跟隨蜂和偵查蜂4種基本要素。使用ABC算法進行電梯優化調度時，蜜源對應于群控電梯優化問題的一個可行解，其收益率即適應度值代表解的質量。每個雇傭蜂對應一個確定的蜜源也就是解向量，在不斷迭代過程中對蜜源的鄰域進行搜索。

基本ABC算法在搜索開始階段，引領蜂根據式(10)搜索新蜜源：

vij=xij+φij(xij-xkj)

(10)

式中，j∈{1,2,…，D}，D為待優化問題參數維度，i∈{1,2，…，SN}，k∈{1,2，…，SN}，SN為種群規模，φij為[-1,1]之間的隨機數。

引領蜂在完成搜索后，會回到蜂巢進行資源分享，采用搖擺舞的方式將信息傳遞給跟隨蜂，跟隨蜂對蜜源的選擇概率根據式(11)使用輪盤賭的方式進行，其中fit1為第i個蜜源的收益率，蜜源越豐富，被跟隨蜂選擇的概率越大。

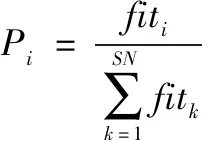
(11)

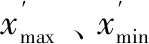
(12)

模擬退火(SA)算法不僅是一種啟發式隨機搜索方法，而且還是一種有效的全局優化算法，它的凝結源于固態物理退火過程，是由Kirknatrick于1983年提出并首次應用于組合優化問題[14-15]。SA算法采用Metropolis驗收準則，該算法在搜索策略過程中可以避免陷入局部最優，其原因是在模擬退火的優化過程中，較好地解決方案被完全接受，較差的解決方案也以一定的接受概率被接受，增加了算法的多樣性。

SA算法中退火溫度T決定蜜蜂接受低收益率食物源的概率，溫度T越高則蜜蜂接受低收益率食物源的概率越大，溫度T越低則蜜蜂接受低收益率食物源的概率越小，因此算法初期溫度T應該較大使得算法趨于全局搜索，迭代后期溫度T越小使算法越趨于局部重點搜索，加快算法收斂速度。因此，溫度下降函數 選取如式(13)所示：

T(t+1)=λT(t)

(13)

式中,λ為退火系數，一般取值范圍為[0.9，1)。

2.2 基于ABC-SA算法的電梯群控系統派梯策略

基本ABC算法中偵察蜂的功能是保證算法跳出局部最優，收斂到全局最優，但對復雜的優化問題進行求解時算法往往很難收斂到全局最優。引領蜂和偵查蜂在進行鄰域搜索后利用貪婪選擇策略進行蜜源選擇，對初期適應度值較差的蜜源缺乏關注，提前將有潛力的蜜源淘汰，尋優過度依賴算法優化前后蜜源好壞，忽略擁有巨大潛力的蜜源。為進一步挖掘潛力蜜源，避免ABC算法求解多目標問題時陷入局部最優解，從算法選擇機制角度出發，引入模擬退火擴大選擇機制，提出一種混合ABC-SA算法來解決EGCS優化調度問題。所提ABC-SA混合算法是一種結合人工蜂群算法的快速計算優勢以及模擬退火利用高溫狀態下粒子的高速無序性，有效避免陷入局部最優解的方法以提高全局搜索能力。混合算法可以拓寬解的搜索方向，加強算法的全局搜索能力，并且根據模擬退火的特性，初始溫度在較高的情況下，算法容易接受惡化解，從而能夠跳出局部最優解，減少算法對初始解的依賴。而通過緩慢地降低溫度T，當T趨于零時不再接受惡化解，逼近全局最優解，此過程對整體算法后期求解更加有益。

模擬退火的選擇策略如式(14)所示，fit(xi)、fit(xj)為原始蜜源的適應度和鄰域搜索后新蜜源的適應度。若fit(xj)>fit(xi)，則接受新蜜源；若fit(xj)?fit(xi)，則以概率計算公式接受新蜜源。模擬退火的選擇策略在一定程度上保留了原有算法貪婪選擇策略的擇優選擇思想，同時也以一定的概率接受有潛力的蜜源，在一定程度上增強了基本ABC算法跳出局部最優的能力。

(14)

在群控電梯優化調度中，根據某一時刻每臺電梯當前所在狀態樓層、電梯內信息、呼梯信號信息、侯梯人數等數據對1.2節所建目標函數進行優化，優化過程是尋找評估函數極值的過程。基于ABC-SA混合算法的EGCS調度流程如圖1所示。

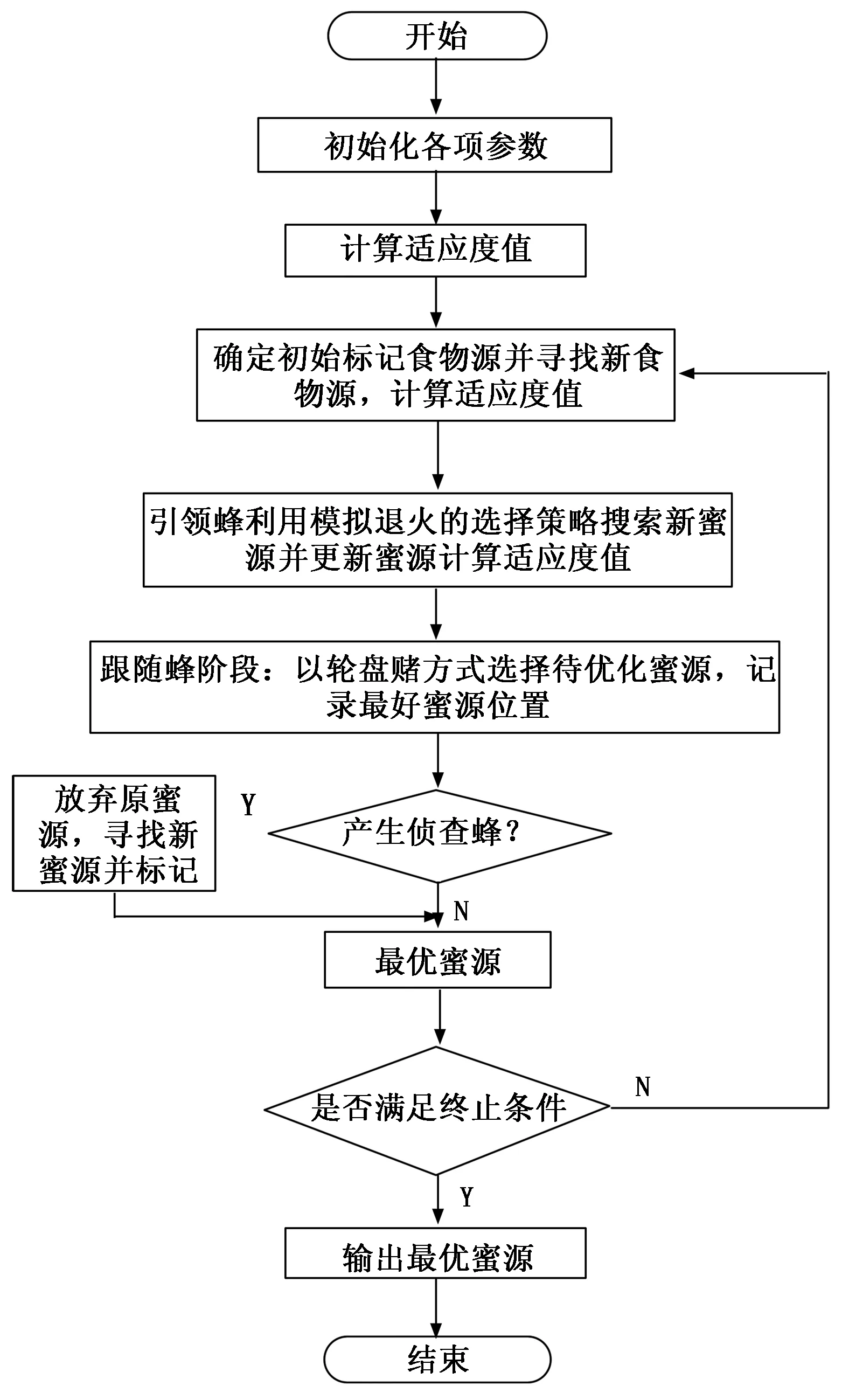
圖1 基于ABC-SA算法的EGCS調度流程圖

Step1：初始化算法參數，如種群規模SN、蜜源限制開采次數limit、最大迭代次數Maxcycle、模擬退火的初始溫度T等；

Step2：蜜源初始化并計算其適應度值；

Step3：雇傭蜂(引領蜂)階段。按照式(10)進行鄰域搜索尋找新食物源并計算適應度值；

Step4：進行模擬退火操作。當引領蜂進行鄰域搜索后，利用貪婪選擇策略進行蜜源選擇，盡管可以較快地找到局部最優的蜜源，但會失去當前適應度不高且更接近于全局最優的蜜源。利用模擬退火的選擇概率，比較原始食物源和新食物源的適應度，若新食物源適應度大于原始蜜源的適應度，則接受該食物源，否則以式(14)求出的概率接受新食物源。

Step5：跟隨蜂階段。根據式(11)計算食物源的概率，依照概率選擇食物源；

Step6：判斷是否有要放棄的蜜源，若有偵查蜂產生，則放棄原蜜源按照式(12)尋找新蜜源并標記；若沒有偵查蜂，更新最優蜜源，記錄當目前為止最優解；

Step7：判斷是否達到循環終止條件，若滿足循環結束，輸出最優蜜源，否則返回Step3繼續搜索。

2.3 模型約束

利用混合模擬退火改進人工蜂群算法解決電梯群控調度問題時，應充分考慮電梯當前運行狀態和運行邏輯，即模型約束條件：

1)當電梯產生m個向上的呼梯信號時，此時電梯首先響應較低樓層的乘客，然后再響應較高樓層的乘客。

2)當電梯計劃服務于n個下行信號的乘客時，電梯首先承載較高樓層的乘客，然后再承載較低樓層的乘客。

3)電梯實際載重量超過額定載重量時，不響應任何呼梯信號。

4)行駛過程中，當同時有向上或向下的呼梯請求時，電梯順應當前行駛路徑預先響應相同方向的信號。

5)分散待機策略：無任何呼梯請求時，電梯均勻分布于各個樓層為自由梯狀態；上高峰時間段內，電梯均處于基層呈基梯狀態。

3 模擬仿真及結果分析

3.1 模擬仿真

為驗證混合ABC-SA算法應用于電梯群控系統派梯調度策略的有效性，以常見辦公大樓3部電梯24層建筑物群控電梯系統作為模擬對象，當前狀態下設置樓層內電梯運行情況參數如表2，仿真代碼在Matlab平臺上編譯。

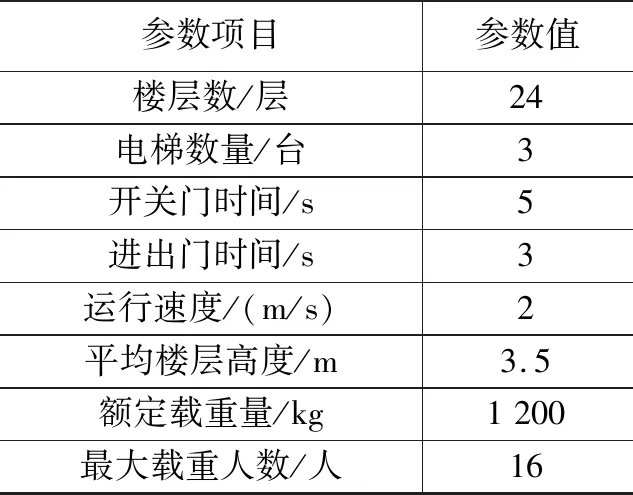
表2 EGCS群控電梯參數

分別進行上高峰、下高峰、層間交通模式3種情況下的仿真實驗，目標函數的權重系數取值如表3所示。上高峰模式下人群密集，乘梯需求多集中于基層并向上行駛，且上高峰多發生在早上上班期間，以輸送人流為主要目的，因此乘梯時間、侯梯時間、系統能耗權重分別為0.4、0.65、0.1。下高峰多發生在下班期間，以輸送乘客為主，乘梯時間、侯梯時間、系統能耗權重設置為0..4、0.4、0.2；同理層間交通模式下人流量少以能耗為主時間性能為輔，權重設置分別為0.2、0.2、0.6，在不同模式權重下對群控電梯進行多目標調度仿真研究。

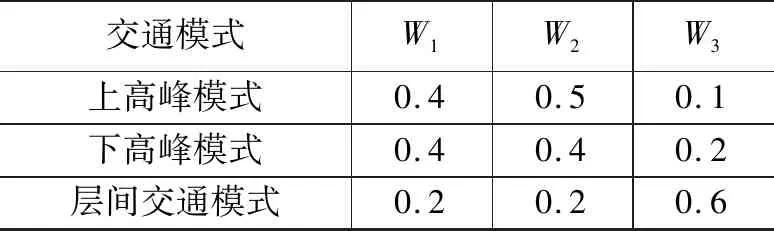
表3 不同交通模式下的權重

3.2 結果分析

針對1.2節建立的多目標優化函數，在Matlab仿真軟件中采用基本ABC算法和混合ABC-SA算法對3.1節所設置的三3種不同模式進行仿真研究，群控電梯多目標優化前后適應度曲線對比結果如圖2～4所示。

由圖2～4可以看出，基本ABC算法在3種模式下均容易陷入局部最優解，而改進的ABC-SA混合算法卻能跳出局部最優最終達到全局最優解。且在基本ABC算法調度下上高峰、下高峰和層間模式的適應度分別為0.378、0.31和0.295，ABC-SA算法調度下適應度分別為0.395、0.357和0.314。可以看出無論處在哪種交通模式下，混合ABC-SA算法優化后的適應度值結果都優于基本ABC算法的求解結果，選擇適應度大的結果進行派梯，驗證了混合算法的有效性。

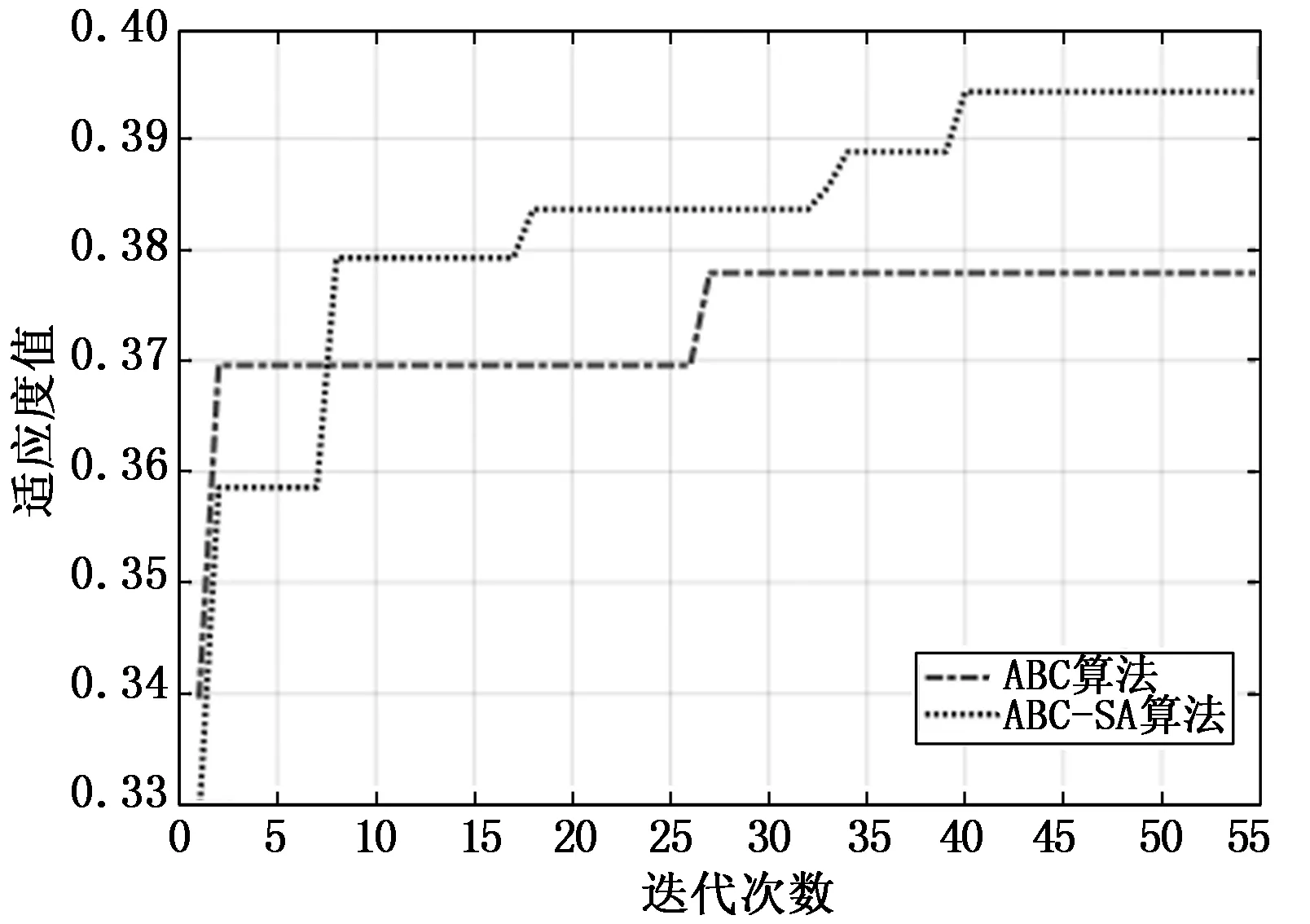
圖2 上高峰模式兩種算法的收斂對比圖

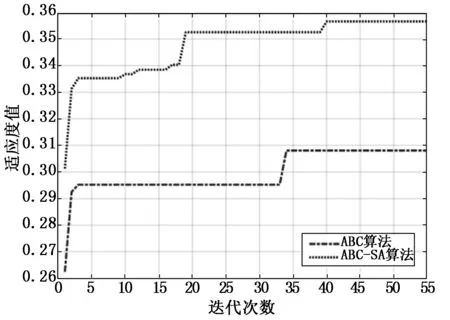
圖3 下高峰模式兩種算法的收斂對比圖

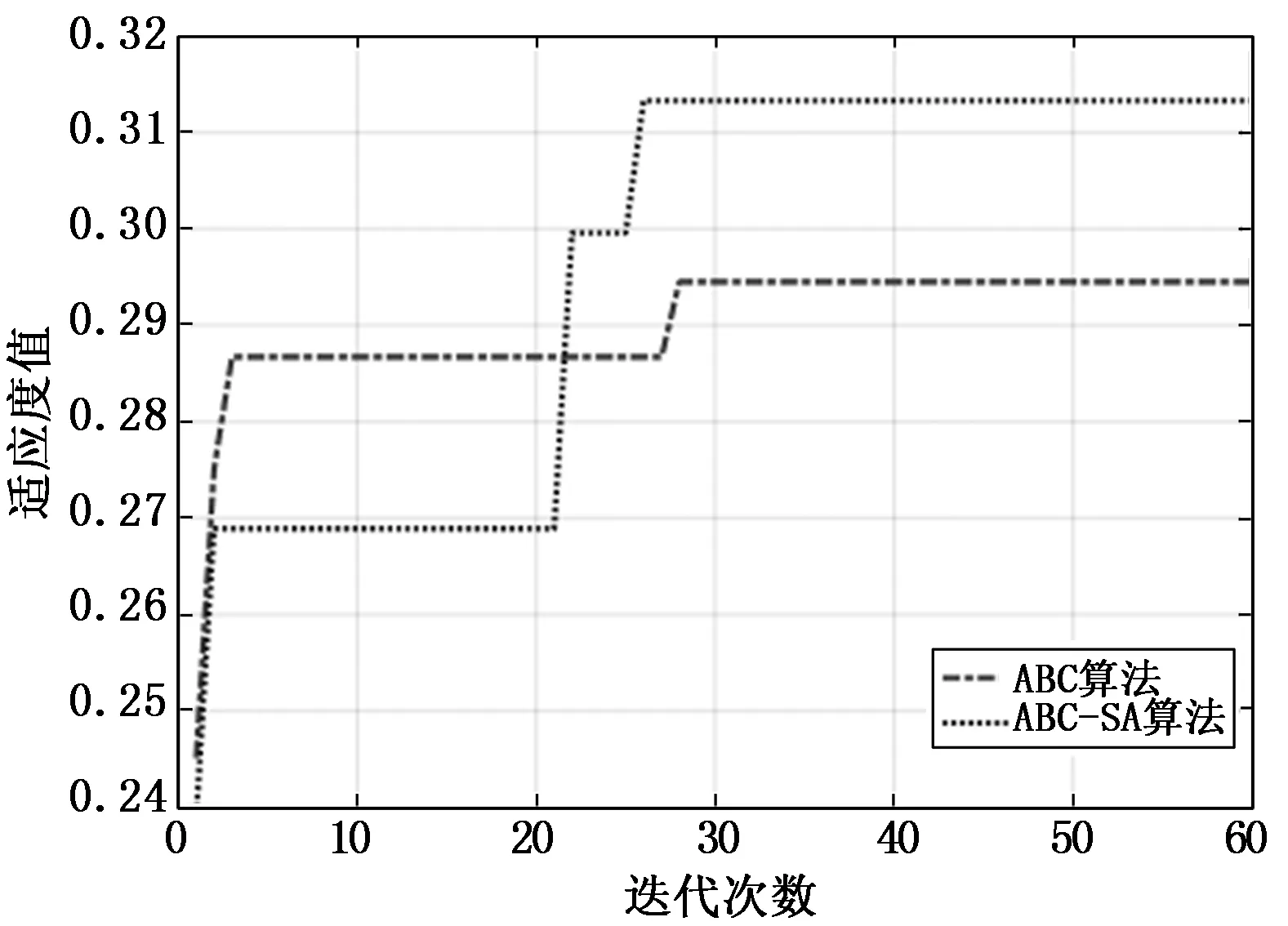
圖4 層間模式兩種算法的收斂對比圖

為進一步說明結果的有效性，通過對平均侯梯時間、平均乘梯時間、停靠次數的多組數據進行優化，然后取各指標值的平均值。表4～6為上高峰模式下混合ABC-SA算法與基本ABC算法進行比較的仿真結果。仿真數據表明，與基本ABC算法相比，混合算法的平均候梯時間，平均乘梯時間以及停靠次數的平均值都有不同程度的提高，ABC-SA算法下的平均等待時間減少19.69 s，平均乘梯時間減少4.57 s，停靠次數減少4次，各項重要指標均比較理想，其衡量電梯群控系統的3大指標性在混合ABC-SA算法下均比基本ABC算法有所提高。

表4 平均侯梯時間比較 s

表5 平均乘梯時間比較 s

表6 停靠次數比較 n

表7為兩種算法在3種模式下的各指標數據值，可以看出在不同的交通模式下，ABC-SA算法的求解質量相對于基本ABC算法的求解質量具有一定優勢。尤其是在上高峰和下高峰模式，ABC-SA算法的優勢比層間模式下的優勢更為明顯。其仿真結果表明了該算法具有一定的可行性和有效性，能有效地提高群控電梯系統的性能和服務質量。

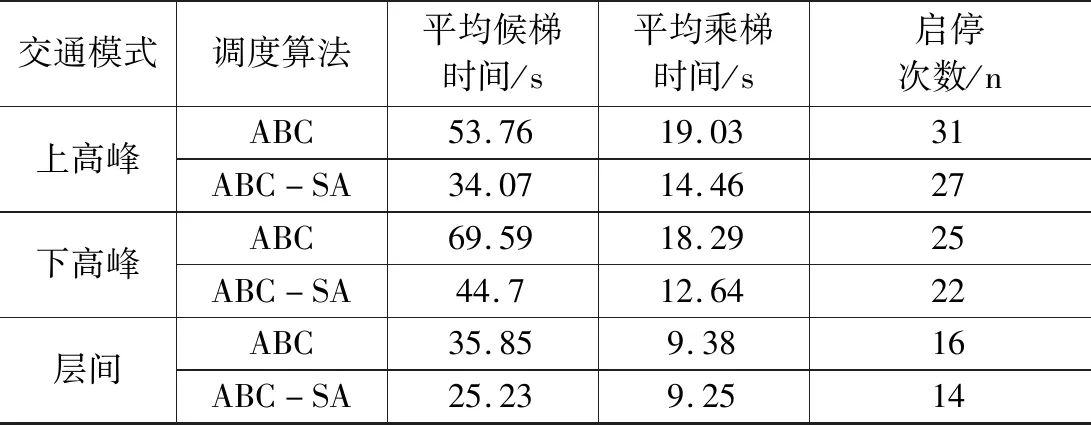
表7 不同模式下調度算法對比

4 結束語

電梯群控系統具有龐大的狀態空間和隨機的乘客到達等特點，且需同時兼顧乘客的時間請求以及能耗請求，這使得調度問題變得復雜。文中提出一種混合改進的人工蜂群算法實現對群控電梯優化調度策略的研究，通過確定影響群控電梯性能的關鍵因素建立多目標數學模型，根據基本人工蜂群算法求解易陷入局部最優解進而引入模擬退火思想改善算法性能，經仿真研究ABC-SA混合算法求解結果相對于基本人工蜂群算法在乘梯時間、侯梯時間和停靠次數方面均有一定提高，對電梯群控系統多目標調度的優化有一定的應用參考價值。