風擾動對機載單站無源定位精度影響分析*

劉文躍,彭世蕤,何 緩,王廣學

(空軍預警學院, 武漢 430019)

0 引言

提取相位差變化率定位法以其快速高精度的定位特點在機載單站無源定位中得到了廣泛應用[1-4]。該定位方法的關鍵在于獲取高精度的相位差變化率參數[5]。然而在實際應用中,受常值風、突風和大氣紊流等風擾動影響[6-9],載機在飛行過程中會發生飛行姿態擾動,從而使固定在無人機機身上的干涉儀基線矢量指向發生變化,對相位差變化率的高精度獲取產生影響,從而影響定位精度。

在實際應用中,風擾動是不可避免的,因此研究風擾動對機載單站無源定位的影響具有較強的現實意義。基于此,文中建立了風擾動下的無人機運動模型,并分別討論分析了在常值風、突風、大氣紊流3種典型風擾動下,采用經典卡爾曼濾波法提取相位差變化率后的定位精度[10]。對無人機載單站無源定位技術的實際運用具有一定的指導意義。

1 風擾動下的無源定位原理

1.1 相位差變化率定位法的定位精度模型

如圖1所示,以地面某固定點為坐標原點建立固定坐標系ogxgygzg,ogxg軸指向正東方向,ogyg軸指向正北方向。XOY為機體坐標系,OX沿機身軸指向機頭方向,OY指向右側機翼,OA構成干涉儀基線。R表示無人機和目標間的徑向距離，β表示目標方位角,β′表示干涉儀波達角。對于地面固定目標,當目標與載機距離較遠時,可以忽略飛行高度,等效至二維平面。無人機姿態可用歐拉角(偏航角、俯仰角和滾轉角)描述。由于在二維平面內不需考慮俯仰角,并且干涉儀位于無人機機身軸上時,無人機發生滾轉時不會對相位差及其變化率的測量產生影響,因此無人機姿態只考慮偏航角φ。

圖1 風擾動時一維干涉儀定位示意圖

從圖中可以看出β′=β+φ。根據空間關系和相位差變化率的定位原理可推出[11]:

(1)

從式(1)可由看出,風擾動帶來的姿態變化φ對定位結果直接產生了影響,然而在實際應用中,通常假設無人機做勻速直線運動無姿態變化,即令式(1)中φ=0,此時定位模型變為:

(2)

這顯然會引入定位誤差:

(3)

式中:δx、δy分別表示x、y方向的定位誤差；xT、yT表示無人機真實位置坐標;x′T、y′T表示無人機忽略風擾動帶來的姿態變化得到的位置坐標。

定義定位精度δ:

(4)

為了量化分析風擾動對定位精度帶來的具體影響,還需要量化風擾動對無人機飛行姿態的影響。

1.2 風擾動下的無人機運動學模型和航跡模型

無人機的六自由度運動學方程為[12]:

(5)

式中:θ、φ、ψ為歐拉角；p、q、r為對應歐拉角角速度;γ、χ為航跡角。以上無人機運動參數的詳細定義見文獻[12]。va、vk、vw分別表示無風擾動時無人機的飛行速度矢量,有風時無人機的飛行速度矢量和風速矢量,三者有以下矢量關系:

vk=va+vw

通過以上關系就可以將風速作為參量引入無人機運動學模型中。再通過式(5)可以得到風擾動下無人機的實時姿態角,量化了風場對無人機飛行姿態的具體影響。

ΔP=vk·Δt

(6)

式中:ΔP表示航跡點采樣間隔內的航跡矢量;Δt表示采樣間隔。則通過式(6)可以給出無人機的飛行航跡信息。

2 典型風場擾動模型

1)常值風

常值風表現為風的大小和方向為確定值[13],即υw(t)=C,C為某確定常數。

2)大氣紊流

大氣紊流是指疊加在平均風上的連續隨機脈動,平均風是風速的基準值[13]。大氣紊流模型一般采用Dryden模型或Von Karman模型,其中Dryden模型的頻譜形式簡單,是有理式,可以作因式分解,便于紊流場的數值仿真,因此文中選擇Dryden模型進行大氣紊流的仿真。

仿真的基本原理是將白噪聲通過成形濾波器得到符合一定功率譜的有色噪聲,其中的關鍵是確定傳遞函數G(s)。3個速度分量的傳遞函數為[14]:

(7)

圖2 Dryden模型橫向紊流片段(Lu=200,σu=1.14 m/s)

3)突風

突風又稱陣風,表現為確定性的風速變化,在工程應用中,通常采用1-cos型突風結構,其數學模型為[15]:

(8)

式中:x表示無人機的飛行距離,單位為m;vm代表突風強度,表示突風風速的最大值,單位為m/s;dm代表無人機在突風區飛過的距離。

將不同風擾動模型代入無源定位模型中,就可以量化分析風擾動對機載單站無源定位帶來的具體影響。

3 仿真分析

由于只考慮二維平面,因此風擾動情況只考慮無人機橫向和縱向兩個擾動分量,忽略垂直方向。

3.1 常值風對機載單站無源定位影響的仿真分析

無人機基本仿真參數設置如下:無人機平行大地平面做勻速直線運動,無姿態擾動時飛行速度為150 m/s,無人機初始位置為(0,0),另外在無人機運動學模型中引入傳感器自身帶來的測量誤差,假設在橫、縱向速度分量誤差滿足均值為0、方差為0.5 m/s的高斯分布,并定義風向角η為風速矢量與無人機機頭方向的夾角。

風向角η固定為15°,取常值風速大小分別為v=5 m/s,15 m/s,25 m/s時(依據風力等級劃分參考表,分別代表微風、疾風、狂風),仿真結果如圖3。

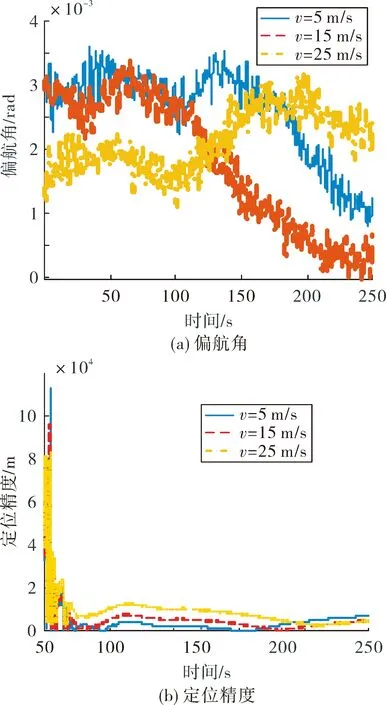
圖3 風速改變時常值風影響下的偏航角和定位精度

從仿真結果可以看出,在姿態角方面,姿態角抖動程度相當,可以認為常值風的風速大小對無人機姿態角的影響較小。在定位誤差方面,可以看出定位誤差均在開始階段有較大幅度波動,而后穩定在一定水平,這是因為在定位過程中采用卡爾曼濾波法提取相位差變化率,由卡爾曼濾波先波動后穩定的特點造成了這樣的仿真結果。還可以看出,隨著常值風速的變大,定位誤差也隨之增大,為了更加直觀地表達誤差,取經過100 s(從圖中3可以看出此時定位誤差趨于穩定)后的定位精度的均值作為平均定位精度進行分析,單位為km,表達式如下:

(9)

式中:δi表示第i時刻的定位誤差,n1取t=100 s時刻對應的采樣點數,n2=n1+2 000,即共選取2 000個采樣點共計100 s的誤差計算定位精度。

則誤差數值如表1所示。

表1 常值風風速影響下誤差水平對比

風速大小固定為15 m/s,取常值風風向角分別為η=15°,45°,75°時,仿真結果如圖4。

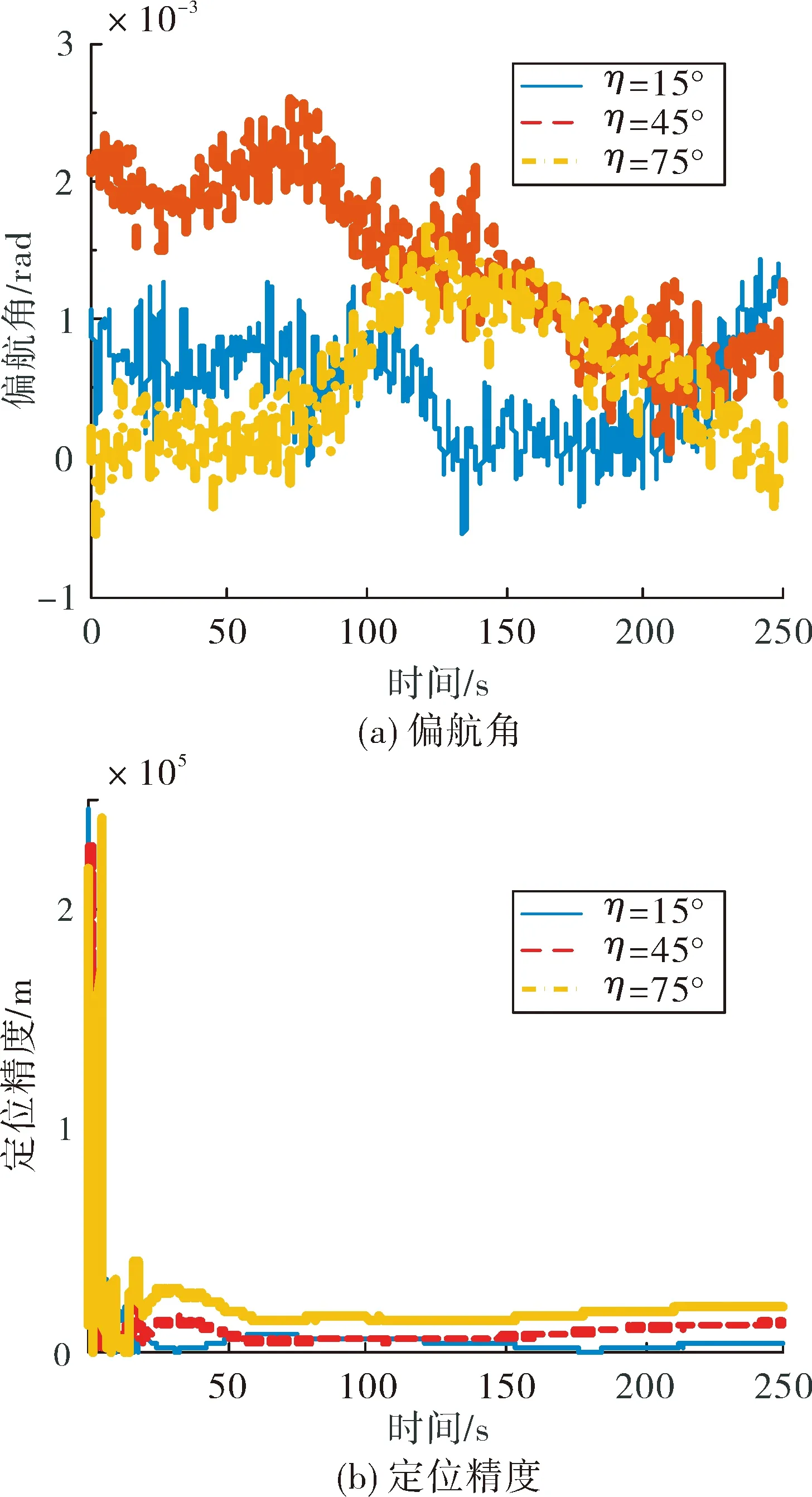
圖4 風向改變時常值風影響下的偏航角和定位精度

從上述仿真結果可以看出,常值風的風向角變化對無人機偏航角的影響同樣較小,而隨著風向角的變大,定位誤差也隨之加大。這是因為風速可以矢量分解為沿無人機機頭方向與沿無人機機翼方向的兩個速度分量vwx和vwy,vwx和vwy即為風速帶來的速度誤差,隨著風向角的變大,vwx變小,vwy變大,而且無人機自身在沿機頭方向本來就有較大的飛行速度,因此vwx帶來的相對誤差較小,在仿真條件下速度的相對誤差不超過17%,而在機翼方向,無人機的飛行速度在風的影響下風速大小由基本為零變為vwy,即速度誤差呈幾何倍數增長,機翼方向風速的相對誤差很大,因此風向角的變大會使定位誤差加大。具體誤差如表2示。

表2 常值風風向影響下誤差水平對比

綜上,風擾動為常值風時,風速的大小和方向均會對無源定位結果產生影響,并且造成影響的主要原因是風速影響了無人機的飛行速度。

3.2 大氣紊流對機載單站無源定位影響的仿真分析

在進行仿真分析時,為了更加貼合實際,令無人機橫向、縱向和垂直向上均受大氣紊流影響,然后取無人機航跡在大地平面的投影以及偏航角代入定位模型進行計算。

根據文獻[13],令紊流尺度Lu=2Lv=2Lw=200 m,并假設風具有各向同性,即各個方向的紊流強度相等,令σu=σv=σw=σ,當紊流強度大小分別為σ=1.14 m/s,1.84 m/s,2.54 m/s時,根據仿真得到的對應最大紊流風速均不超過6 m/s,根據文獻[13]對紊流強度的等級劃分,以上設置的紊流強度均屬于“微弱”等級,仿真結果如圖5。

圖5 大氣紊流影響下的偏航角和定位精度

從仿真結果可以看出,紊流強度變大時,無人機偏航角抖動加劇。從定位誤差看,在3種紊流強度下,利用經過卡爾曼濾波提取得到的相位差變化率計算出的定位誤差在一定時間后均能收斂到一定誤差值,按照式(9)計算平均定位精度如表3所示,但是明顯可以看出,紊流強度越大,收斂速度越慢,并且未收斂前的誤差越大。

表3 大氣紊流影響下誤差水平對比

從表中可以看出,用卡爾曼濾波提取相位差變化率的方法在大氣紊流強度微弱時仍難以達到理想效果,這是因為卡爾曼濾波在待濾波序列呈線性變化時效果最佳,在無人機做勻速直線運動時相位差線性程度較高,然而風擾動造成的姿態變化導致了相位差的線性程度下降。這也說明了姿態角的抖動會對定位結果產生較大影響。

綜上,風擾動為大氣紊流時會對無源定位結果產生影響,并且造成影響的主要原因是大氣紊流造成了無人機姿態角的抖動。

3.3 突風對機載單站無源定位影響的仿真分析

突風的仿真條件設置如下:突風尺度為dm=200 m,突風開始時刻為100 s,突風風向角為15°,突風強度分別為vm=5 m/s,15 m/s,25 m/s時,仿真結果如圖6(只顯示風速變化對應時間段內的仿真結果)。

圖6 風速改變時突風影響下的偏航角和定位精度

從仿真結果可以看出,突風會對無人機飛行姿態和定位結果造成較大影響,當突風出現時,無人機姿態會產生較大幅度的擾動,并且在突風的影響下,定位誤差隨突風強度變大而變大,這也說明了采用卡爾曼濾波法提取相位差變化率的方法在無人機受到突風擾動時難以得到較好的定位結果,顯然突風導致的姿態變化同樣導致了相位差的線性程度下降。同樣取100 s(突風開始時刻)后的誤差計算誤差水平如表4。

表4 風速改變時突風影響下誤差水平對比

當突風強度為vm=15 m/s,突風風向角分別為η=15°，45°,75°時,仿真結果如圖7。

圖7 風向改變時突風影響下的偏航角和定位精度

從仿真結果看出,風向角變大,同樣對無人機偏航角受到的擾動變大,并且無源定位誤差越大,具體誤差情況如表5。

表5 風向改變時突風影響下誤差水平對比

綜上,突風會使無人機姿態在短時間內發生較大幅度的擾動,并且在突風的影響下,經過卡爾曼濾波提取相位差變化率后的無源定位結果仍存在較大誤差。

綜合以上3種情況的仿真分析可以得出如下結論:1)當風擾動為常值風時,需要準確估計出無人機在風擾動下的飛行速度才能更加有效地定位;2)當風擾動為突風時,無人機飛行姿態短時間發生較大改變,此時定位誤差顯著增加,并且由于相位差在風擾動下的非線性程度提高,采用卡爾曼濾波提取相位差變化率的方法難以有效提高定位精度,并且在突風與常值風強度相當時,突風帶來的定位誤差更大;3)當風擾動為大氣紊流時,無人機的飛行姿態角會受到擾動,定位誤差顯著,采用卡爾曼濾波提取相位差變化率的方法仍難以有效提高精度,并且在紊流強度微弱時的定位誤差要大于狂風強度下的常值風與突風帶來的定位誤差,可以認為大氣紊流對定位結果的影響最為顯著。綜上所述,風擾動對機載單站無源定位的影響不容忽視,需要提出一些新的技術與方法來對這一影響進行補償。

4 結束語

文中從常值風、大氣紊流、突風3種典型風場擾動出發,量化分析了風擾動對測相位差變化率的機載單站無源定位技術的影響,對該定位方法的實際應用具有參考價值。同時得出了風擾動會導致相位差的線性化程度降低,采用經典卡爾曼濾波提取相位差變化率難以有效提高定位精度的結論,因此還需要研究風擾動下的相位差變化率的提取方法來提高風擾動時的定位精度。文中雖然只考慮了二維平面的擾動,但是，其分析方法同樣適用于三維定位模型。