旋轉齒筒式水力空化器內空化過程

袁惠新，王赟冰，付雙成，周發戚，周龍遠，陸健

常州大學機械工程學院江蘇省綠色過程裝備重點實驗室（常州 213164）

在一定溫度下，液體中由于局部低壓（低于相應溫度下該液體的飽和蒸汽壓）使液體蒸發而引起的微汽泡爆發性生長的現象被稱為空化初生[1]，當液體壓力回復時，汽泡群潰滅。這種汽泡群在液體中生長、發展、潰滅及由此發生的一系列物理、化學反應被稱為空化。空化泡在潰滅時瞬間產生巨大能量并在流體中形成強射流，泡面射流速度可達100 m/s[2]，可使大分子主鏈上的碳鍵斷裂，同時破壞微生物細胞壁，使得高分子有機物降解并且使微生物失活。水力空化可以用于強化許多工藝過程及污水處理和生物化工等方面[3-6]，空化技術在食品工業處理方面也有了迅速和更為廣泛的發展[7]。空化技術可應用于液態食品的殺菌、混合、均質和乳化等加工過程，朱孟府等[8]研究發現利用水力空化設備可有效去除水中的有機物和微生物，其中大腸桿菌的去除率達99.99%。

常用的水力空化裝置主要有孔板和文丘里管兩種[9]，此類空化器結構簡單，空化強度低，無法滿足工業上大規模、高效的處理要求。除此之外，射流管、液哨及齒盤式空化器等新一代水力空化裝置尚處于實驗室研究階段且空化強度仍不理想[10-11]。與空化形式單一的靜設備相比，旋轉齒筒式水力空化器產生空化的機理是由復雜流場中各種力復合而成（以剪切力和離心力為主），擺脫了傳統的產生空化方式，可在空化器內產生群空化，空化強度大、空化效率高，因此對空化器空化性能的研究具有重要意義。

采用計算流體力學軟件Fluent 19.0模擬齒筒式水力空化器的基本空化性能，以及齒結構參數對空化性能的影響。分析空化器內空化發生機理、流體空化特性，從而對齒筒空化器的進一步探索、優化和應用做出貢獻。

1 計算模型、計算方法及邊界條件

1.1 計算模型

以在前人基礎上改進的旋轉齒筒式水力空化器為例研究，并對其結構做了優化[12]。齒筒式空化器主要由靜筒和轉筒組成，轉筒直徑160 mm。如圖1所示，靜筒與轉筒同軸，靜筒上具有凸出的齒，轉筒上具有盲孔，齒孔間形成的空間為物料流動通道，空化則發生在轉筒的盲孔內。靜筒上的齒和轉筒上的盲孔在軸向等距分布有9圈，齒孔軸向對齊，周向等角度分布有20個。靜筒上的齒（定齒）與轉筒表面有一定間隙（2 mm），形成剪切空間。圖1中（a）（b）分別為圓齒靜轉筒，（c）（d）分別為正方形齒靜轉筒。其中，方齒橫截面與圓齒橫截面積相同，圓齒橫截面半徑為6 mm。

圖1 物理模型

采用ANSYS ICEM軟件進行網格劃分，將流體模型分為4個部分：入口區域、轉筒盲孔區域、定齒間區域和出口區域，以interface面進行連接。其中入口區域與出口區域采用結構化網格，轉筒盲孔和定間區域采用非結構化網格，網格總數分別為2 416 738（圓齒）和2 439 727（方齒）。生成的流體區域網格如圖2所示。

圖2 網格劃分結果

1.2 計算方法及邊界條件

利用計算流體軟件ANSYS Fluent進行運算，選用壓力基瞬態求解器；選用Mixture多相流模型，不考慮氣液兩相間的相對運動；采用Realizable k-ε湍流模型，模型可更好地模擬圓孔射流問題；壁面處理采用增強壁面函數；選用Zwart-Gerber-Belamri空化模型，劉厚林等[13]研究表明，在大流量系數下，該空化模型的預測精度更高；壓力速度耦合采用PISO算法，其他項均選用具有絕對穩定特性的一階迎風格式。

Realizable k-ε湍流模型中湍動能及耗散率輸運方程為：

式中：C1=max[0.43η/（η+5）]，η=S×k/ε，Gk由平均速度梯度引起的湍動能產生；Gb由浮力影響引起的湍動能產生；YM為可壓縮湍流脈動膨脹對總的耗散率的影響；C1ε、C2ε、C3ε、C2為經驗常數，FLUENT中默認值為C1ε=1.44、C2ε=1.92、C3ε=0.09、C2=1.9；σk、σε分別為湍動能和湍動耗散率對應的普朗特數，FLUENT中默認值為σk=1.0、σε=1.3；k和Sε是用戶定義的湍動能項和湍流耗散源項。

模擬采用速度入口、壓力出口以及無滑移標準壁面函數邊界條件。處理量為0.2 m3/h，操作壓力為1個大氣壓。流體介質設置為常溫下的水。設置動齒間區域網格為動網格，計算收斂精度為10-5，進行數值模擬。

2 齒筒式空化器的空化機理

齒筒式空化器的空化初生機理主要分為以下兩部分。基于伯努利方程的機械剪切力造成的渦空化，流體流經限流區域時，流速增大，壓力下降，從而產生空化。定齒與轉筒盲孔相對處為限流區域，由于定齒的存在，使得流體流動面積突然變小，從而起到限流作用。經節流后的流體流入轉筒盲孔，流體得到釋放，壓力回復，空泡潰滅。Bernoulli方程：

式中：ρ為液體密度，kg/m3；p為壓力，Pa；v為流動速度，m/s。由此可得，液體中的壓力p與流速v的關系是流速越大，壓力越小，反之亦然。

另一個是由離心力造成的空化。盲孔內液體的受力分析如圖3所示（重力在高轉速下忽略不計），由于轉筒高速旋轉，流體受到慣性離心力Fc的作用，液體產生向盲孔外運動的趨勢，則在盲孔底部會產生壓力損失，使壓力降低至低于大氣壓值，壓差隨流體向外運動速度的增加而增加，此壓差會作用給液體一個壓差力Fp方向向內。筒內空化反應穩定時，兩力平衡，此時流體不再向外運動，Fc=Fp，即：

即：

式中：ρ為液體密度，kg/m3；V為盲孔內液體體積，m3；r為半徑，取盲孔深度的一半到轉筒軸線的長度，m；ω為轉速，rad/s；p1為盲孔內負壓壓力，Pa；p2為盲孔外壓力，Pa；A為盲孔的橫截面積。由式（4）可根據轉速計算出盲孔內負壓力的值。

圖3 盲孔內液體受力分析

3 計算結果與分析

3.1 速度分布

圖4是定齒分別為方齒和圓齒的情況下，轉速3 000 r/min空化器中流體的相對速度分布圖。流體流經限流區域時流體中的氣核進入剪切層后被具有較低渦心壓力的相干渦結構“吸入”，并生長形成空泡。從圖5局部放大圖中可看出，液體流入轉筒盲孔后在底部形成一個漩渦，這是由于液體進入盲孔后，盲孔內的液體徑向速度大，周向速度小，而盲孔外液體由于轉筒旋轉帶有較大的周向速度，因此在盲孔內局部區域形成一個周向速度梯度，進而形成漩渦。隨著旋轉速度的增加，漩渦中的湍流強度也會增加，這將可能造成瞬態空化的產生，以空化為基礎的化學轉變只能在瞬態空化條件下才能形成，因此，此漩渦的存在直接影響空化產量及空化器的應用層面。

3.2 壓力分布

圖6分別為圓齒和方齒時空化器內的壓力云圖。由伯努利方程可知，在定齒間存在低壓區域。由圖7可看出定齒間的低壓區域主要分布在齒前緣，這是由于轉筒轉動過程中，轉筒盲孔與定齒前緣先接觸，此時盲孔內低壓流體對定齒間流體會有一個“抽吸”作用，因此對定齒前緣區域造成負壓，同時這也使得盲孔內的低壓區域向節流點偏移。由于方齒齒間區域較圓齒齒間區域“封閉性”更好，即齒間流體在受到“抽吸”作用而流出后不易有其他區域的流體流入補充其所損失的壓力，因此，方形定齒間會有局部負壓區域存在，而圓形定齒間則沒有。

由離心液壓理論公式可知速度與壓力呈正比，在盲孔內最外側會有一個高速液壓現象，而低壓區域只在靠近旋轉中心的盲孔內產生，從圖中可以看出，盲孔底部壓力值已達到飽和蒸汽壓。由于在方孔和圓孔橫截面積相同的情況下，方孔周長大于圓孔周長，即剪切長度更長，因此方齒盲孔內的負壓區域較圓齒空化器面積更大，空化泡也更容易得到充分發展。

圖4 圓齒和方齒z軸截面相對速度云圖

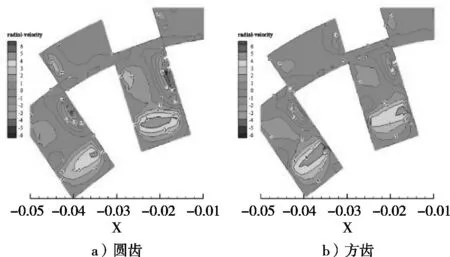
圖5 圓齒和方齒z軸截面局部放大相對速度云圖

圖6 圓齒和方齒z軸截面壓力云圖

圖7 圓齒和方齒z軸截面壓力云圖

3.3 汽相體積分數分布

圖8 給出圓齒和方齒時空化器內的汽相分布云圖。低壓是空化初生的要素之一，結合圖5可知，汽相產生區域大致與負壓區相對應，方齒空化器內的空化區域略大于圓齒空化器。在流體剛進入空化區時，汽含率（產生的空泡體積占負壓區體積的百分比）為20%～30%，流體在負壓區內充分發展以后空化率達到95%，甚至100%，由此可知流場中足夠的低壓段（合適的轉子盲孔深度）是確保空化泡集聚能量時間，即空化泡發展時間的重要因素。

圖8 圓齒和方齒z軸截面汽相分布云圖

如圖9所示，對比2種齒型空化器內的空化泡體積分數占比（空泡相體積分數占流體總體積分數的比值），結果表明，轉速為3 000 r/min時，方齒空化器比圓齒空化器空化泡體積分數占比高出14.3%。同時，空化器內初期的空化過程尚未達到穩定，因此在前0.5 s內，會出現空化泡體積分數占比波動較大的情況，此后空化器內空泡產生總量隨旋轉時間的增加而平穩發展，這說明在齒筒式空化器內的空化過程是一個連續且穩定的過程。在此基礎上，分析不同轉速下方齒空化器內空化泡體積分數占比隨旋轉時間的變化規律。如圖10所示，隨著轉速的提高，空化器內局部壓力逐漸降低，負壓區域占比也隨之增大，空化區域面積隨轉速增大而增大，區域內空化泡體積分數亦隨之增大。這說明，適當提高轉速更有利于空泡初生，從而可以提高空化效率。基于這一規律，后續可繼續考慮增大剪切面積對該齒筒式空化器進行優化研究。

圖9 3 000 r/min時方齒和圓齒空化器中空化泡體積分數占比隨旋轉時間變化曲線

圖10 不同轉速下方齒空化器中空化泡體積分數占比隨旋轉時間變化曲線

4 結論

采用數值模擬的方法分析齒筒式水力空化器內的流場，從而研究空化機理。

結果表明：（1）空化器內的空化由離心力和剪切力復合形成。一方面流體經過靜齒筒時受到剪切力作用，另一方面，轉筒高速旋轉，盲孔內液體受到強烈的慣性離心力作用，兩種作用力復合，使得空化現象在盲孔內產生。（2）隨著轉速增大，負壓區域隨之增大，空化效率更高。（3）改變靜、動齒筒上面齒的形狀，將圓齒改為方齒，可以增大剪切面積，有利于提高空化率。（4）齒筒式空化器在運行過程中，空化過程連續穩定，與其他現有空化器相比，具有空化區域大、空化率高的優點，并且可以根據需要，增減齒筒長度，達到增減剪切空化次數的目的，在工業應用上更為靈活方便。