讓課堂成為學生的尋“理”之旅

曹素萍

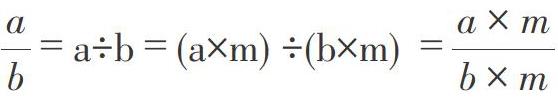
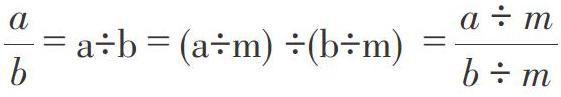
【摘要】引導學生展開尋“理”的學習探究過程，可以幫助學生真正理解和掌握這一知識。感知性質之原理、體會驗證方法之學理、尋悟性質之算理，學生在尋“理”中不僅體會到了知識的本質和科學的學習方法，還能發展理性思維能力，根植理性精神。

【關鍵詞】尋理 知識本質 理性思維

《分數的基本性質》這節課是學生在學習了商不變的規律、分數的意義、分數與除法的關系的基礎上進行的，是進一步學習分數的約分和通分、分數四則運算的基礎，是分數教學的一個關鍵點。教材先讓學生通過看圖寫分數、折紙操作找分數，感受分子、分母不同的分數中分數的大小可以相等。再觀察分子、分母的變化，從而歸納出分數的基本性質。最后要求學生用整數除法中商不變的規律說明分數的基本性質，加深對分數基本性質的理解，建立新的認知結構。教學中，大部分教師都按教材的編排進行教學，學生也能掌握分數的基本性質，但因為牽引過多，學生未必真正理解分數基本性質的本質，數學思考力的培養也是有缺失的。

筆者在執教這一課時，充分調動學生已有的學習經驗，引導學生自主展開尋“理”的學習探究過程，從而幫助學生深刻體會知識本質，掌握科學的學習方法，發展理性思維能力，根植理性精神。

一、復習猜想，感知性質之原理

數學猜想是人的思維在探索數學規律、本質時的一種策略，是一種創造性的思維方式。它能縮短解決問題的時間，獲得數學發現的機會。猜想不是胡思亂想，而是建立在已有事實和經驗基礎上的。在數學學習過程中，有意識地引導學生進行猜想，能調動學生探究的熱情，培養學生的創新意識和探索精神。

師：（板書：商不變的規律）什么是商不變的規律？

生：被除數和除數同時乘或除以相同的數（0除外），商不變。

師：分數與除法有哪些聯系？

生：分數的分子相當于被除數，分母相當于除數，分數值相當于商，分數線相當于除號。

師：結合商不變的規律和分數與除法的關系，猜想一下分數中可能會有什么規律？

生：分數的分子和分母同時乘或除以相同的數，0除外，分數值不變。

師：（板書學生猜想的內容）如果請你們給這個規律取個名字，可以叫它什么？

生：分數值不變的規律。

原理是帶有普遍性的、最基本的，可以作為其他規律的基礎規律。整數除法中，商不變的規律既是分數的基本性質的學習基礎，也是分數基本性質的原理。五年級的學生已具有一定的知識遷移和類推的能力，所以很容易就猜想到分數值不變的規律（即分數的基本性質），猜測的同時也初步感知了性質的原理。猜想是否正確、這個規律是不是叫“分數值不變的規律”，都不重要，重要的是這個規律是學生自主猜測的結果，模糊和不確定性更增強了自主驗證的需求。

二、合作探究，體會驗證方法之學理

“尋”，是追尋、尋求、尋根究底，這里兼有“循”之意。尋“理”既指學生在課堂學習中自主地尋找學科知識的“原理”，亦指在活動中學會遵循學科的學習方法之“學理”，數學猜想和驗證就是學生學習數學的有效方法。而驗證活動不僅要關注教材本身蘊含的知識目標，更要關注的是驗證的過程和方法。如何讓驗證分數基本性質的方法更科學、合理呢？

1.正反舉例驗證

師：大家準備怎樣驗證自己的猜想呢？

生1：可以先寫一個分數，將它的分子和分母同時乘或除以一個相同的且不等于零的數，得到一個新的分數，再用學過的方法證明這兩個分數大小相等。

生2：我準備先找到兩個大小相等的，分子、分母不同的分數，再觀察分子和分母是否同時乘或除以了相同的數。

師：大家想到的方法都很好，正向和反向驗證更能增加結論的說服力。典型的分數更具代表性，所以建議大家用來驗證的分數最好既有真分數，又有假分數。

學習小組合作驗證，填寫研究小結（A或B），匯報交流。

2.演繹推理驗證

師：通過剛才正反驗證，你們得出的結論是什么？

師：分數有無數個，你們剛才只驗證了幾十個分數。幾十個分數有這樣的規律，所有分數都一定有這樣的規律嗎？

生：……

師：有沒有更具有概括性、更合理的方法來驗證呢？

（學生思考）

生：我們猜想的規律是從商不變的規律和分數與除法的關系而來，能不能用它們來證明分數值不變的規律呢？

師：問得好！讓我們用字母表示數來試一試。（師生共同驗證，師相機板書）

師：分子和分母同時除以相同的數怎么驗證？（指名學生驗證）

師：這樣驗證時，哪些字母不能為零？為什么？

生：b和m都不能為零，因為它們是分母和除數。

師：孩子們，現在我們可以確定這個規律是正確的嗎？這個規律在數學上還有一個自己的名字，叫“分數的基本性質”。

科學的驗證方法有操作驗證、舉例驗證和推理驗證等。推理包括合情推理和演繹推理，合情推理是從已有的事實出發，憑借經驗和直覺，通過不完全歸納和類比等推測某些結果。學生前面的猜想和舉例驗證的過程都是合情推理，它看似合情合理，實際上卻有可能是錯的。演繹推理是從已有的事實和確定的規則出發，按照邏輯推理的法則證明和計算。用商不變的規律和分數與除法的關系來驗證分數基本性質是演繹推理，因為推理依據的規律和關系是真的，所以結論一定是正確的。學生在驗證活動中合作探究，不僅尋找到了分數的基本性質之“原理”——商不變的規律，而且體驗到了科學的驗證方法之“學理”——正反舉例驗證和合情推理與演繹推理結合驗證。如此設計，不僅讓學生在知其然中知其所以然，更能讓學生感受到理性思維的嚴謹與縝密，發展了理性精神。

三、練習提升，尋悟性質之算理

史寧中教授在《注重“過程”中的教育》這本書里提出：“課不要反復講，而要把握數學的本質……應該把理給講出來。”這里的數學本質就是數學道理。那么，分數基本性質的本質是什么？或者說運用這個性質時的算理又是什么呢？教材中練習十的第1題要求孩子們在方格紙上涂色表示12/24，再思考還可以表示幾分之幾。我是這樣引導學生思考尋“理”的。

師：涂色部分還可以表示幾分之幾？

生：6/12、 4/8、 3/6、 2/4、1/2?。（師板書）

師：這些分數大小相等嗎？為什么？

生1：都表示同一個涂色部分。

生2：分子和分母的變化相同。

師：從分子、分母的變化中，你能發現什么？

生：方格紙平均分的份數擴大或縮小幾倍，涂色部分的份數也就擴大或縮小相同的倍數。

師：這里分數的什么變了，什么沒變？

生：分子、分母變了，分數的大小不變。

師：分母變了，也就是什么變了？分子變了，也就是什么變了？

生1：分母變了，就是分數單位變了。分子變了，就是分數單位的個數變了。

生2：我發現分數單位變大了，分數單位的個數就少了;分數單位變小了，分數單位的個數就多了。

生3：分數單位擴大多少倍數，個數就縮小相同的倍數;分數單位縮小多少倍數，個數就擴大相同的倍數。

教學中，通過數形結合學生們發現了：平均分的份數的變化和涂色部分的份數的變化是相同的;分子、分母變了，本質上就是分數單位和分數單位的個數變了，因為分數單位和分數單位個數的變化是有規律的，所以分數的大小不變。

總之，在小學生現有的認知水平上激發他們合理、有度、有效地追尋數學之“理”，不僅能使學生的認知更通透，更能促成師生關系、教學結構等方面的深度變革。

（作者單位：江蘇省南通市通州區通州小學）