初中數學發散思維能力的培養策略分析
吳利輝

【摘要】教學改革對教師學科素養、文化素養、教育教學技能的要求越來越高。教師不但要注意對學生基礎知識、基本技能的培養,而且要重視學生的發散思維能力、邏輯思維能力、自主創新能力的培養。其中,發散思維能力的培養關系著學生分析問題、解決問題的能力提升和個人的成長。文章就初中數學發散思維能力的培養策略展開了分析。
【關鍵詞】初中數學;發散思維能力;培養策略
在初中數學教學中,經常存在學生聽課認真,知識點熟練,課后練得多,但是成績總不理想,對數學的興趣降低。究其原因,最根本的是學生的發散思維能力沒得到鍛煉,做不到舉一反三,由此及彼。發散思維,又稱輻射思維、發射思維、擴散思維或求異思維,是指大腦在思考時呈現一種擴散狀態的思維模式。它表現為思維視野廣闊,思維呈現維發散狀,是創造性思維最主要的特點[1]。教師要善于引導、啟迪學生獨立觀察、思考、分析和推理。學生的發散思維能力在日積月累中得到逐步鍛煉、塑造和養成,久而久之,就會逐步減少對教師的依賴,擺脫對例題簡單機械模仿,領會知識精髓,從例題中跳出來,對所學知識融會貫通,活學活用。
整體和部分是辯證統一的。學生個體的數學思維能力得到提高,成績提升,會推動班級整體思維能力提升與班級發展。教學中認識和運用數學思維及其發展規律,無論對學生個體成長還是對集體成長、教育事業發展,意義都非同一般。如何培養初中數學發散思維能力?筆者認為可以從六個方面入手。
一、科學安排教學內容,擦亮思維火花
教學中教師要善于不斷改革教學方法,及時更新教學內容[2]。雖說教師教學、學生學習都要立足課本,但“以本為本”并非照本宣科,一成不變,而是要把握和領會課本的思想精髓。科學合理地設置教學內容,需要教師結合我國的數學發展歷史,以史為鑒;綜合考慮教學現狀,實事求是;根據學生的具體情況,對癥下藥。教學內容的選取設置要符合學生的認知規律,符合邏輯思維規律,符合學生的實際情況。
美國哲學家教育家約翰·杜威說:“教育即生活。”教師要帶領學生走出課堂,在參加社會生活的實踐中發現數學思想的魅力,擦亮思維的火花。中國教育家陶行知提出“生活即教育”。教師要深入社會生活、學生生活,善于發現融入時代內容、體現時代精神的生活素材,挖掘其中的數學思想。同時要深入鉆研和挖掘教材,做出篩選,選出符合學生理解能力、富有啟發聯想價值的數學知識。此外,“興趣是最好的老師”,教師還要培養學生數學興趣,發揮其主觀能動性,拓展思維,提高創新能力,由舊知推動新知的獲得。
二、巧妙設置問題情境,啟迪思維發散
明代顧炎武在《與友人論學書》寫道:“前輩學貴有疑,小疑則小進,大疑則大進。疑者,覺悟之機也,一番覺悟,一番長進。”數學學科富有邏輯性、條理性、系統性,對空間感、立體感要求也強。學生如果缺乏抽象性思維能力,學習中就可能遇到各種困難。教師要通過創設教學情境,設置一連串富有啟迪思維而又層層遞進的問題,有的放矢。教師還要鼓勵學生質疑,主動探究,獨立思考,啟迪思維發散,在探究中體會數學樂趣,在合作中提高抽象思維能力與數學應用能力。
三、合理引導自主探究,尋求思維多樣
目前在初中數學教學中,不少教師依舊采用傳統的灌輸式的教學方法傳授理論知識。這種傳統的教學方式會降低學生學習興趣,不利于活躍學生思維,更不能激發學生的學習熱情,會影響教學活動的正常有效開展。教師要引導學生開展自主探究活動,鼓勵學生求知,找尋問題答案,在探究中學會思考和分析,靈活應用,鍛煉和提高數學分析應用能力。自主探究讓學生參與到知識的生成過程中,深入理解知識,提升創新思維的能力,培養學生良好的學習習慣[2]。
例如,在學習合并同類項時,教師可以開展一些師生互動,準備一些零錢,讓學生幫助自己數錢,一方面激發了學生的學習興趣,另一方面加深了學生對知識點的理解。在師生互動中,有的學生把相同金額的紙幣放在一起,有的學生則是一張一張地數。無論他們使用哪種方法,最后得到的結果都是一樣的。這時教師可以組織學生深入交流,引出合并同類項這個知識點,然后分小組進行討論,讓學生自主學習。這不僅加強了師生、生生之間的交流,還調動了學生的學習積極性。學生在體會知識的生成過程中,感受到成功解決問題的快樂。在實踐中創造和發展數學知識,在實踐中獲得和享用數學知識,學生的發散思維能力和自主學習能力在自主探究中得到提高。
四、全面構建知識體系,明晰思維條理
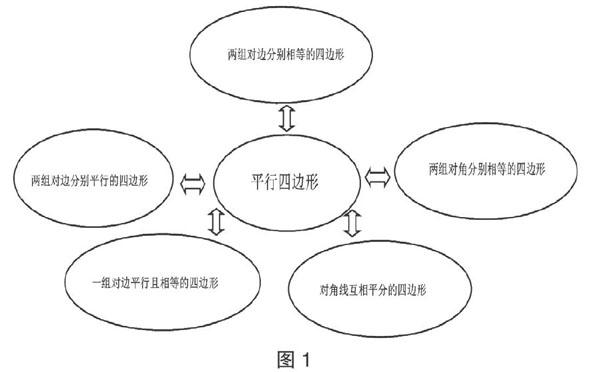
傳統的復習基本上都是教師帶領學生直接回憶已學知識,回憶相關定義、概念、公式等等。這種機械性的復習不僅達不到復習的目的,還有可能增加學生對數學學科的厭煩。在平時的新課學習中學到的是一個個零碎的細小知識點,它們大多以碎片形式呈現,不成體系。我們要充分利用好復習課,將碎片化的知識連點成線,連線成面,連面成體,將知識系統化。知識的系統化呈現可以是教師設置好知識樹,也可以嘗試讓學生親自動手完成這一過程。耳聽不如眼看,眼看不如手動,學生親自動手實踐,可以鍛煉學生發散思維,培養動手操作能力。教師應鼓勵學生自己動手,整理各個部分知識中的概念、公式,尋找它們之間的聯系,畫出思維導圖,自主構建清晰的數學知識理論體系。在整理繪制思維導圖的過程中,學生系統地理解知識,明晰思維條理,從而提升了發散思維能力和分析歸納能力。
例如,平行四邊形的判定方法可構建如下思維導圖(圖1)。
五、積極鼓勵一題多解,助推思維擴散
“條條大路通羅馬。”在數學學習中,學生普遍能做到多題一解,但對給定的題目能做到一題多解者微乎其微,原因在于思維無法發散,容易形成定勢。教師要引導、倡導學生主動參與,鼓勵他們采用多樣化的解題方法,提高他們對一題多解的認知水平和思維能力。解題方法的多樣化不僅有利于學生積極思考,相互交流分享,培養思維多向性能力,而且有利于促進學生創新能力的發展。
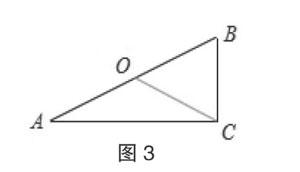
例如,在證明“直角三角形中角所對直角邊等于斜邊的一半”時,可以引導學生思考添加不同輔助線的方法,充分鍛煉學生的思維能力,提升學生的推理能力。
解法1:“補短”即延長到點,使,連結。
解法2:“截長”即取的中點,連結。
又如,已知經過且與交于點,求不等式組的解集。可引導學生從數、形兩個角度思考,鍛煉學生的計算能力,樹立數形結合思想,提升學生的思維能力。
六、深入挖掘典型例題,輔助思維拓展
課本中的典型例題是開展教學的寶貴資源,起著開山引路的作用,是學生進行模仿、變式、領悟、理解的基礎,也是解題的示范。教學中常出現學生課堂上聽得懂,課后作業難以獨立完成的現象。針對這種現象,教師要對典型例題、習題進行變式,在不斷變式中讓學生體會其中的數學思維,領悟知識內部的深層次聯系,把握知識的內在結構,使學生反思理解領悟知識,鍛煉思維。
例如,人民教育出版社《數學》八年級下冊47頁:如圖4,在中,、分別是、的中點,求證:四邊形是平行四邊形.
變式1:如圖,在中,、分別在、上,且,求證:四邊形是平行四邊形.
變式2:如圖,在中,、分別在、上,且,求證:DE∥BF.
變式3:如圖,在中,、分別在、上,且DE∥BF,求證:.
對例題進行變式訓練,不變圖形,變化條件。在觀察、分析、比較、思考中,調動了學生的積極性、主動性和創造性,產生“以不變應萬變,萬變不離其宗”的解題效應。變式訓練讓學生從常規的題海戰術中解放出來,既減少了不必要的機械重復,節省了大量的時間,減輕了繁重的課業負擔,又拓展提高了學生的思維能力,達到了事半功倍的教學效果。
綜上所述,學生數學思維能力的培養,不僅關系教育教學的成效,而且關系學生的成長。教師可通過科學設置教學內容,創設良好的學習情境,引導學生自主探究,構建知識體系,鼓勵一題多解,挖掘典型例題方式等培養學生的數學發散思維能力。
【參考文獻】
王濤.初中數學課堂中學生發散性思維能力的培養[J].新課程導學,2018(11):96.
畢建華.初中數學教學中學生發散性思維能力培養策略探究[J].新課程·中學,2018(04):180.

