一一對(duì)應(yīng)揭示植樹問題本質(zhì)及數(shù)學(xué)模型的根本

許華庚 劉萍

【案例背景】

“植樹問題”是人教版五年級(jí)上冊第七單元“數(shù)學(xué)廣角”的教學(xué)內(nèi)容，本單元主要滲透有關(guān)植樹問題的一些思想方法，通過現(xiàn)實(shí)生活中一些常見的實(shí)際問題，讓學(xué)生從中發(fā)現(xiàn)一些規(guī)律，抽取出其中的數(shù)學(xué)模型，然后再用發(fā)現(xiàn)的規(guī)律來解決生活中的一些簡單實(shí)際問題。

“植樹問題”的教學(xué)是五年級(jí)上冊的一個(gè)重難點(diǎn)，而在平時(shí)的教學(xué)中，老師們的課堂會(huì)稍顯局促，或是注重例題的講解而忽略了學(xué)生的自主性與創(chuàng)造性，或是加強(qiáng)了練習(xí)的強(qiáng)度忽視了教會(huì)學(xué)生把握知識(shí)的本質(zhì)。

【案例描述】

面對(duì)同樣的“植樹問題”，老師們的教法卻是各不相同的：

1.有的老師是借助畫圖的方法進(jìn)行教學(xué)，并讓學(xué)生從中發(fā)現(xiàn)規(guī)律。“植樹問題”是一種比較抽象、易錯(cuò)的問題，如果借助畫圖就比較簡單、直觀，只要學(xué)生掌握了畫圖的方法，就一定能找到正確答案。

2.有的老師是創(chuàng)設(shè)情境把問題留給學(xué)生，讓學(xué)生在解決問題的過程中摸索找到三種不一樣的植樹方法，進(jìn)而根據(jù)方法的不同來依次探討解決問題。

3.有的老師是從較小的植樹棵數(shù)和間隔數(shù)起，不斷增加兩個(gè)量，讓學(xué)生在兩個(gè)量的不斷變化中找到其中蘊(yùn)含的規(guī)律，并熟悉規(guī)律后運(yùn)用規(guī)律來解決類似問題。

4.有的老師是借助“植樹問題”的三個(gè)模型直接來理解植樹棵數(shù)與間隔數(shù)的關(guān)系，學(xué)生在理解數(shù)量關(guān)系的基礎(chǔ)上進(jìn)行解決問題的練習(xí)與鞏固。

……

那么，究竟什么樣的方法對(duì)學(xué)生而言，既能夠解釋知識(shí)的本質(zhì)，又能開發(fā)學(xué)生的思維？既對(duì)植樹問題具有一個(gè)全面的了解，又能在學(xué)生想不起來的時(shí)候伸出手掌就知道植樹問題怎么解答呢？究竟是應(yīng)用數(shù)形結(jié)合中通過圈一圈、一一對(duì)應(yīng)思想解開學(xué)生心目中“間隔±1”是怎么得來重要，還是學(xué)生粗枝大葉、迷迷糊糊、被動(dòng)接受植樹問題的數(shù)學(xué)模型重要？

【案例解決】

一、在“一一對(duì)應(yīng)”中引入課題

1.兩棵小樹十個(gè)杈，不長葉子不開花。能寫會(huì)算還會(huì)畫，天天干活用到它。（打一人體器官）

2.猜到“手掌”的同學(xué)把你的小手舉起來。

3.在手指之間能找到間隔嗎？（圖①）

4.什么是間隔？（圖②）

5.存在間隔或者間距的地方，生活中有許多，如圖③，那么，什么是植樹問題？

小結(jié)：生活中與間隔（數(shù)）有關(guān)的類似問題，就叫“植樹問題”。

二、用“一一對(duì)應(yīng)”的思想探究植樹問題模型

1.按照“一一對(duì)應(yīng)”的方法，圈一圈、數(shù)一數(shù)、填一填，創(chuàng)造兩端都栽的數(shù)學(xué)模型。

師：按從左到右的順序一個(gè)人和一個(gè)間隔對(duì)應(yīng)為一組、一個(gè)人和一個(gè)間隔對(duì)應(yīng)為一組圈在一起，最后還剩下（1）位小朋友。即：①總?cè)藬?shù)=間隔數(shù)？茌（1）

【在學(xué)生明確如何應(yīng)用“一一對(duì)應(yīng)”圈的基礎(chǔ)上，放手讓學(xué)生探索總?cè)藬?shù)與間隔數(shù)之間的關(guān)系。學(xué)生很容易根據(jù)自己圈的結(jié)果得出總?cè)藬?shù)=間隔數(shù)+1。即后來所歸納的植樹棵數(shù)=間隔數(shù)+1。】

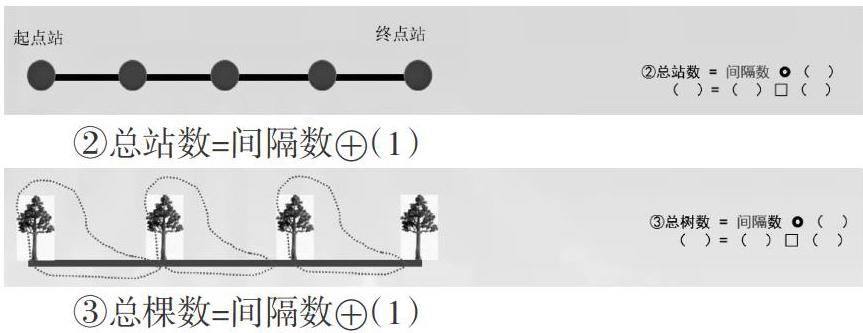
②總站數(shù)=間隔數(shù)？茌（1）

③總棵數(shù)=間隔數(shù)？茌（1）

④我發(fā)現(xiàn)“植樹問題”形式一：（條件：兩端都栽）植樹棵數(shù)=間隔數(shù)+1。

小結(jié)：我們利用一一對(duì)應(yīng)圈一圈的過程中驗(yàn)證創(chuàng)造出“兩端都栽的植樹問題模型”：植樹棵數(shù)=間隔數(shù)+1。

師：這個(gè)1代表的究竟是什么？

生：1代表的是“1個(gè)人”“1個(gè)車站”“1棵樹”。

師：1個(gè)人加上4個(gè)間隔得到的應(yīng)該是5個(gè)人？還是5個(gè)間隔？還是5個(gè)間隔人？還是5個(gè)人間隔？好像單位不對(duì)耶？

生：“1個(gè)人”加上“4個(gè)間隔”得到的應(yīng)該是5個(gè)人。

師：為什么“1個(gè)人”加上“4個(gè)間隔”得到的是5個(gè)人，“4個(gè)間隔”可以換成“4個(gè)人”？

生：因?yàn)槲覀冊谌σ蝗Φ倪^程中已經(jīng)確認(rèn)了“4個(gè)間隔”和“4個(gè)人”存在“一一對(duì)應(yīng)”的關(guān)系，所以，“1個(gè)人”加上“4個(gè)間隔”得到的是5個(gè)人。

師：誰來對(duì)照課件回答一下：“1個(gè)車站”加上“4個(gè)間隔”為什么會(huì)得到5個(gè)車站？“1棵樹”加上“4個(gè)間隔”為什么會(huì)得到5棵樹？（學(xué)生回答：略）

2.按照“一一對(duì)應(yīng)”的方法，圈一圈、數(shù)一數(shù)、填一填，創(chuàng)造兩端不栽的數(shù)學(xué)模型。

學(xué)生交流匯報(bào)。

【由于學(xué)生已經(jīng)有了第一次“一一對(duì)應(yīng)”圈一圈的活動(dòng)經(jīng)驗(yàn)，本次數(shù)學(xué)模型的創(chuàng)造，學(xué)生思維將更加活躍，學(xué)生很快能夠創(chuàng)造出：（條件：兩端不栽）植樹棵數(shù)=間隔數(shù)-1。】

小結(jié)：我們利用一一對(duì)應(yīng)圈一圈的過程中再次驗(yàn)證，并且創(chuàng)造出“兩端不栽的植樹問題模型”：植樹棵數(shù)=間隔數(shù)-1。

師：這個(gè)1代表的又是什么？是“1盆花”，“1根電桿”，“1棵樹”，還是“1個(gè)間隔”？

生：1代表的是“1個(gè)間隔”。

師：“5個(gè)間隔”減去“1個(gè)間隔”應(yīng)該得到的是“4個(gè)間隔”，為什么會(huì)得到“4盆花”呢？

3.重溫植樹問題的數(shù)學(xué)模型就在手上。

師：其實(shí)，我們剛才應(yīng)用“一一對(duì)應(yīng)”的思想圈一圈創(chuàng)造出的兩種植樹問題數(shù)學(xué)模型，就在我們的手掌上，當(dāng)你想不起來的時(shí)候，你只要伸出手掌就會(huì)想到了。

【讓學(xué)生在此表象的基礎(chǔ)上，再深刻認(rèn)識(shí)與理解記住植樹問題的兩種數(shù)學(xué)模型。】

三、應(yīng)用自己創(chuàng)造出的兩種植樹問題數(shù)學(xué)模型解決問題

1.出示例題。

在全長100米的小路一旁每隔5米植一棵樹（兩端都栽），一共要植多少棵樹？

課件提示：（兩端都栽）：

①間隔數(shù)=（？）？謼？（？）

②共栽棵數(shù)：

2.變式練習(xí)。

在全長100米的小路一旁每隔5米植一棵樹（兩端都不栽），一共要植多少棵樹？

課件提示：（兩端都不栽）：

①間隔數(shù)=（？）？謼？（？）

②共栽棵數(shù)：

四、拓展練習(xí)延伸模型

再次應(yīng)用“一一對(duì)應(yīng)”思想圈一圈、數(shù)一數(shù)、填一填。

再創(chuàng)造：“植樹問題”形式三：

植樹棵數(shù)? 間隔數(shù)

條件：（? ? ? ? ?）

【學(xué)生再次親歷應(yīng)用“一一對(duì)應(yīng)”思想圈一圈，一番有趣的探索后，再次創(chuàng)造出（條件：一端栽、一端不栽）植樹棵數(shù)=間隔數(shù)。】

【案例反思】

平時(shí)的教學(xué)，許多教師都側(cè)重于植樹問題數(shù)學(xué)模型的傳授與應(yīng)用，而忽視了植樹問題數(shù)學(xué)模型的來源于學(xué)生的自主創(chuàng)造能力培養(yǎng)，特別是在植樹問題數(shù)學(xué)模型的溯本求源上更是一個(gè)缺憾。那么，植樹問題數(shù)學(xué)模型的靈魂到底在哪里呢？

1.“一一對(duì)應(yīng)”是學(xué)生創(chuàng)造植樹問題數(shù)學(xué)模型的基礎(chǔ)。

本案例安排的三個(gè)環(huán)節(jié)，都是用“一一對(duì)應(yīng)”的方法，圈一圈、數(shù)一數(shù)、填一填，然后，分別根據(jù)練習(xí)題讓學(xué)生自我發(fā)現(xiàn)、自我創(chuàng)造出植樹問題的數(shù)學(xué)模型：“條件為：（兩端都栽）：植樹棵數(shù)=間隔數(shù)+1”;“條件為：（兩端不栽）：植樹棵數(shù)=間隔數(shù)-1”;“條件為：（一端栽一端不栽）：植樹棵數(shù)=間隔數(shù)”。試想，如果沒有讓學(xué)生采用“一一對(duì)應(yīng)”的方法來圈、數(shù)、填、思，學(xué)生能自我發(fā)現(xiàn)植樹問題的三種數(shù)學(xué)模型嗎？

2.“一一對(duì)應(yīng)”是學(xué)生揭開植樹問題數(shù)學(xué)模型中“1”代表的究竟是什么的關(guān)鍵。

我們平時(shí)的教學(xué)，是不是看重學(xué)生會(huì)不會(huì)做這道題就行了？對(duì)于數(shù)學(xué)模型中的“加1”“減1”是不是一帶而過？

本案例強(qiáng)調(diào)學(xué)生應(yīng)用“一一對(duì)應(yīng)”的學(xué)習(xí)方法自我創(chuàng)造，并對(duì)自我創(chuàng)造出來的“1”進(jìn)行追問，可謂問得巧、問得妙、問得好。

在條件為兩端都栽的情況下，植樹棵數(shù)=間隔數(shù)+1，其中“1”代表的是：“1個(gè)人”“1個(gè)車站”“1棵樹”。

在條件為兩端都不栽的情況下，植樹棵數(shù)=間隔數(shù)-1，其中“1”代表的又是什么？是“1盆花”，“1根電桿”，“1棵樹”，還是“1個(gè)間隔”？

前面的“1”代表的是一個(gè)具體的數(shù)量，而后面的“1”只代表“1個(gè)間隔”。學(xué)生確確實(shí)實(shí)明白了這一點(diǎn)。試想我們平時(shí)教學(xué)后，學(xué)生能夠明白這一點(diǎn)嗎？也只有讓學(xué)生明白了數(shù)學(xué)模型中“1”的含義后，才能為教師后面揭示植樹問題的數(shù)學(xué)本質(zhì)打下基礎(chǔ)。

3.“一一對(duì)應(yīng)”是揭示植樹問題數(shù)學(xué)模型本質(zhì)的落腳點(diǎn)。

我們都知道植樹問題是許多學(xué)生頭痛的知識(shí)點(diǎn)，也是學(xué)生的易錯(cuò)易混點(diǎn)，而易錯(cuò)易混的原因就在于三種條件下植樹棵數(shù)與間隔數(shù)的關(guān)系是不相同的。本案例巧用一一對(duì)應(yīng)思想讓學(xué)生從具體的實(shí)例中建立表象，通過一一對(duì)應(yīng)的圈一圈、數(shù)一數(shù)、填一填去親歷感悟體會(huì)三種條件下的植樹棵數(shù)與間隔數(shù)的關(guān)系，進(jìn)而自我創(chuàng)造植樹問題的數(shù)學(xué)模型，然后再抽象出“植樹棵數(shù)”與“間隔數(shù)”兩個(gè)量之間的關(guān)系，加上老師兩個(gè)層面的追問：“1”代表的究竟是什么？在公式中：1個(gè)人加上4個(gè)間隔得到的應(yīng)該是5個(gè)人？還是5個(gè)間隔？還是5個(gè)間隔人？還是5個(gè)人間隔？“5個(gè)間隔”減去“1個(gè)間隔”應(yīng)該得到的是“4個(gè)間隔”，為什么又得到“4盆花”呢？

在兩個(gè)層面的追問過程中，正是一一對(duì)應(yīng)發(fā)揮了巨大作用，并且也只有通過一一對(duì)應(yīng)的方法，學(xué)生才能根據(jù)“同類量相加減后的單位置換”進(jìn)行相互轉(zhuǎn)化，這才是揭示植樹問題數(shù)學(xué)模型本質(zhì)的良好鋪墊與最佳方法。即：在學(xué)生明確關(guān)系式中每個(gè)部分所代表的含義后，學(xué)生才能在解決問題的時(shí)候不模糊、不混淆、不犯錯(cuò)。

總之，本案例給我們的最大啟示是應(yīng)用一一對(duì)應(yīng)的數(shù)形結(jié)合思想為學(xué)生揭示植樹問題數(shù)學(xué)模型的本質(zhì)，這樣帶領(lǐng)學(xué)生建立植樹問題模型，應(yīng)該是更為有效的教學(xué)方式，它比我們讓學(xué)生單獨(dú)機(jī)械記憶植樹問題的三種數(shù)學(xué)模型更為重要。