基于核心素養考查的高考三角函數分析

謝威星

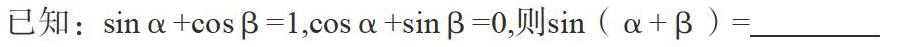
摘 要：隨著課程教育理念的更新與教育改革進程的不斷推進，高中生核心素養的培養受到我國教育部門與一線教師的廣泛關注。三角函數部分不僅是高中數學教育體系中的重要部分，更是高考試題中的重要考點，并且這部分知識所涉及的數學思想與方法對學生解決實際問題具有重要價值意義。本文從核心素養角度對高考三角函數復習方法與習題進行了分析與研究。

關鍵詞：核心素養 高考數學 三角函數

在高中數學課堂實踐中，許多內容要求學生掌握較強的計算能力，但是部分數學教師在引導學生進行專題題型強化過程中，忽視了對學生核心素養與數學思維的發展，即便使學生的解題能力與運算能力得到強化，學生數學素養與思維也難以得到長期發展。因此教師要專題題型分析與核心素養相關聯，注重在課堂訓練過程中貫徹落實對學生數學核心素養的培養。本文選取高考三角函數來進行將復習與解題中的深刻思想與科學價值恰當地形態化，進一步深化學生的數學認知結構發展。

一、培養學習習慣，提高數學素養

從學生角度出發，數學思維特別是數學抽象思維的發展要求學生在復習與練習中養成良好的學習習慣，這就需要教師加強對學生細節處的引導，讓他們對各部分題型所運用的知識點進行積極地思考，增強自身學習規范的意識。在復習與梳理三角函數的概念、定理的講授時，教師要讓學生要緊跟自身思路，形成自己的學習方法。在習題上，教師要悉心指導學生學會仔細審題與分析，并形成解題思路。教師需要在三角函數復習課通過對知識的深入講解以及練習，進而彌補三角函數新授課中學生對知識點把握的靈活度，使得學生將三角函數新授課習得的新概念抽象成自身的解題能力，在解決問題時前后聯系、左右兼顧，從而靈活地運用合適的知識解決問題。

二、建構知識網絡，分析數學思想

復習課中幫助學生有效地進行知識的梳理以及知識網絡的建構，通過聯系新舊知識，讓學生對要復習的知識有一個大體認識，幫助學生在原有知識結構中尋找新概念的附著點，進而產生對新概念更加全面深刻的認識。三角函數復習課需要教師注重一個知識點會從哪些方面考查在復習課中，首先，教師要引導學生回顧知識點，通過板書的形式形成知識點框架體系，注意板書規整，重點突出，并列出框架，對三角函數中有關知識點的異同點以及知識點中蘊含的數學思想和數學方法進行對比，使學生準確把握知識框架。下面進行高考例題分析：

考查要點：本題是基于學生掌握的三角函數的相關概念與公式，深層次觀察學生是否能夠靈活運用數學思想來進行三角函數恒等變化，對學生的綜合運用能力進行考查。

解題誤區：三角函數部分涵蓋較多公式及其用法，若學生沒有認真讀題，則會花費許多時間來回憶或套用公式。

試題思路：在函數學習中學生必須要具備的是函數思想與方程思想，要明確題中的等式關系，再運用方程思想來構造三角函數等式，最后將兩式平方，用公式解決問題。

三、強化習題訓練，提高抽象素養

數學抽象素養的發展是一個循環往復的過程，三角函數習題課可以省略新授課的導入環節，主要是通過學生進行三角函數練習題的訓練完成，即在了解三角函數基礎知識的基礎上對概念以及公式、定理的應用。教師在進行三角函數習題課的教學時，要從概念以及公式定理的本質出發，引導學生對相關概念進行回顧，體會從抽象到具體這一過程，首先需要教師對已知條件進行分析、挖掘所給條件的隱藏含義，從三角函數基礎知識的本質出發，來看待具體題目的求解，進而抽象出解決問題的通性通法，達到“舉一反三”的效果，數學抽象素養的培養反映在學生在現實活動中即為利用數學思維抽象出解決實際問題的方法。下面進行高考例題分析：

考查要點：本題第（1）問較為簡單地觀察學生對余弦定理的應用，而第（2）問則涉及對學生運算、轉化、抽象與推理等素養的考察，對學生數學核心素養要求較高。

解題誤區：不同學生所思考方向不同，其解題難易也就不一樣。若解題中出現差錯，則會導致不必要的失分。第（1）問中主要是部分對正余弦表達式結構認知不夠明確的學生，他們容易在變形與邊角互化環節出現問題。在第（2）問中，除了缺乏解題思路原因，找到解題關鍵的學生容易在構建sin C方程或進行三角變換時找不到去掉增根的方法。

試題思路：

（1）依據題目條件來運用余弦定理解題。

（2）第（2）問有三個解題方向，其一是方程思想：列出關于sin C的方程式;其二是三角變換，要求學生在注意到隱藏條件的基礎上運用輔助角公式，對學生推理素養要求較高;最后是轉化思想，將求解角的問題轉化到邊上，再利用上述做法進行解題。

基于以上闡述與分析，教師要關注到三角函數題中對學生核心素養的考察，并保證學生靈活掌握相關定理與公式。在具體復習課堂中，教師要注重講解概念、定理以及公式的抽象過程。并在習題課中，注重一題多解，進而從簡單的問題中抽象出一類問題的解決方法和思路，使得學生形成對知識的整體框架，加強對練習題的變式訓練。

參考文獻

[1]唐明超.從考題中來回到課本中去——例談高考三角函數復習備考策略[J].中學教研（數學），2019，456（02）：46-48.

[2]薛安定.從轉化視角看2018年高考三角函數問題[J].中學數學教學參考，2018，734（36）：47-48.

[3]梁長春.適應高考對核心素養考查的教學方法探討——以三角函數模型的簡單應用為例[J].明日，2018，000（034）：P.226-227.

[4]何桂琴.數學核心素養在2016年高考三角函數試題中的體現[J].中學數學教學參考，2016（36）.