鐵路斜拉橋鋼混結合段的收縮徐變行為分析

姚亞東，么超逸，楊永清

(1. 內蒙古大學 交通學院，內蒙古 呼和浩特 010020； 2. 中交公路規劃設計院有限公司， 北京 100088；3. 西南交通大學 土木工程學院，四川 成都 610031)

連接鋼結構梁段和混凝土梁段的鋼混結合段是混合梁斜拉橋的關鍵構造和薄弱部位。諸多學者一直致力于鋼混結合段構造形式和受力行為的研究。20世紀80年代，日本學者對生口橋鋼混結合段的構造形式和受力性能開展了研究[1]。1997年，文獻[2]通過模型試驗研究了汕頭礐石大橋鋼混結合段的傳力機制和應力分布，為鋼混結合段的優化設計提供了科學依據。2006年蔣永紅[3]研究了混合梁斜拉橋結合段的剛度等效問題。此外，文獻[4-8]均對特定橋梁的鋼混結合段傳力機制和承載能力進行了數值分析和模型試驗。然而，上述研究主要針對短期荷載作用下公路混合梁斜拉橋的受力性能及傳力機制問題，對鐵路混合梁斜拉橋鋼混結合段在長期荷載作用下收縮徐變行為的研究甚少。由于鐵路混合梁斜拉橋設計荷載更大，結構構造更為復雜，鋼混結合段的素混凝土體積龐大、濕交換較少，且處于空間應力狀態；同時相關研究也表明收縮徐變作用對鋼混結合段受力、變形造成的危害較為顯著[9]，因此迫切需要對鋼混結合段的收縮徐變行為進行專門研究，以期為相似工程提供理論依據和數據支撐。

本文以亞洲最大跨徑的鐵路鋼箱混合梁斜拉橋——甬江特大橋鋼混結合段為研究對象，首先提出了衡量鋼混結合段傳力性能的指標，基于“朱氏預測模型”[10]和彈性徐變理論，遞推出考慮徐變的混凝土本構關系；最后基于Fortran語言對Ansys軟件二次開發，深入研究收縮徐變對鋼混結合段力學行為的影響。

1 傳力指標

文獻[11]中繪制了鋼混結合段混凝土和鋼殼體分擔軸力的比例，見圖1(a),圖1(a)中橫坐標為各測試截面距標準鋼箱梁側剛度過渡段起始截面(0 m處)的距離。5 m處為后承壓板斷面，0～5 m為鋼箱梁段，5～12.35 m為鋼混結合段,見圖1(b)；縱坐標為混凝土、鋼殼體分擔軸力的百分比。

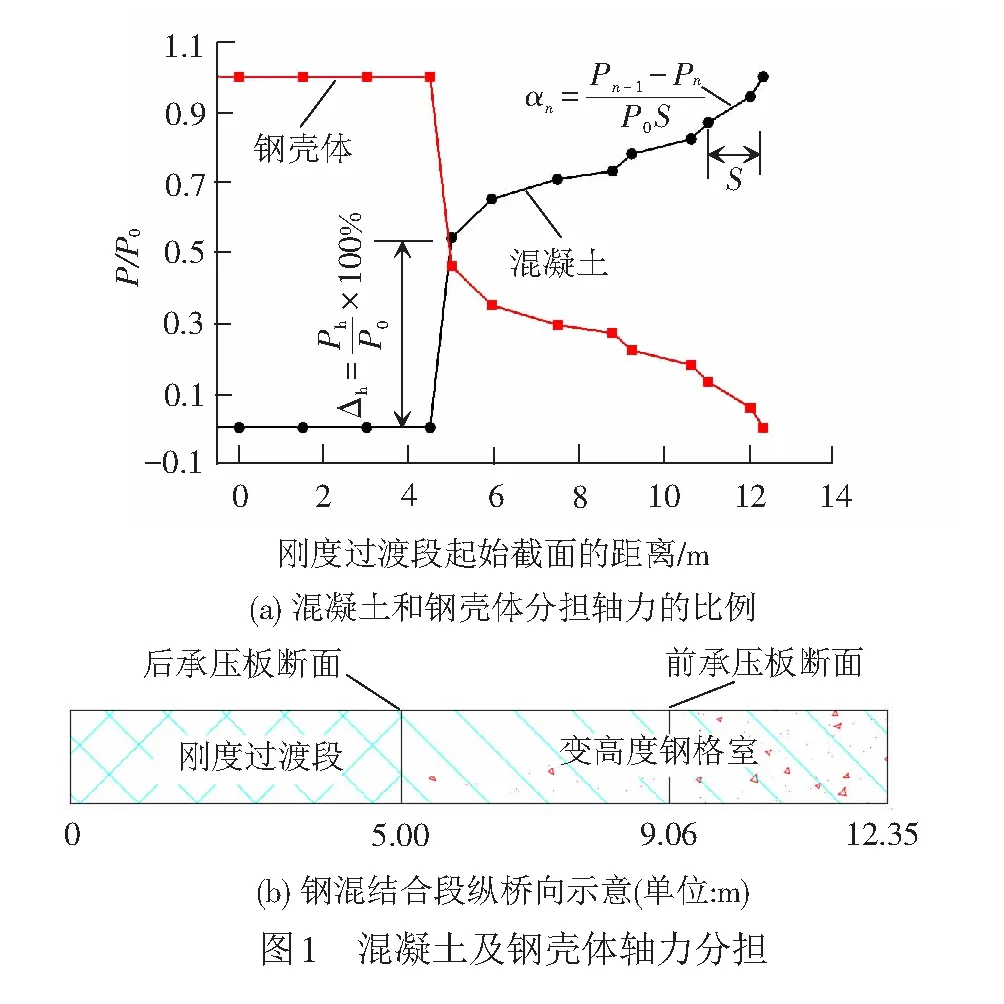
為更好地衡量鋼混結合段的傳力狀況，圖1中傳力指標的定義如下：

(1) 后承壓板傳力率δh:為后承壓板和混凝土梁段間接觸傳遞的軸力Ph與截面總軸力P0的比值，即

( 1 )

(2) 鋼混結合段傳力斜率α：由文獻[9]的試驗結果可知，鋼混結合段端部剪力連接件傳力作用顯著，中部區域剪力連接件作用較弱。為了清晰認識鋼混結合段各排剪力連接件的傳力狀況，沿縱橋向按一定的比例將其劃分成n段，每節段的長度為S。將第n段剪力連接件傳遞軸力占截面總軸力的比例與節段長度S之比定義為第n段的傳力斜率αn，即

( 2 )

同時為深入剖析鋼混結合段剪力連接件的傳力性能，引入平均傳力斜率α、最大傳力斜率αmax，分別見

( 3 )

αmax=max{α1，α2,α3，…，αn}

( 4 )

(3) 鋼混結合段傳力不均勻度δ：通過引入數學中方差的概念來定義傳力不均勻度δ，以此來考察鋼混結合段中剪力連接件傳力的不均勻性及偏離程度，見式( 5 )

δ=

( 5 )

2 收縮的計算

收縮應變與應力歷程無關，可通過施加溫度荷載來模擬收縮作用。本文根據規范CEB-FIP[12]收縮模型計算獲得鋼混結合段核心混凝土的收縮應變ε=-112×10-6，由ΔT=ε/aT可知，欲產生上述收縮應變需施加的溫度荷載ΔT為-11.2 ℃，其中aT為混凝土的線膨脹系數。

3 徐變理論及本構模型的建立

徐變應變與應力歷程相關，對計算式為

( 6 )

式中：ε(t)為t時刻的應變；σ(t0)為t0時刻的應力；E(t0)為t0時刻的彈性模量；C(t,t0)為加載齡期t0的混凝土在t時刻的徐變度。

對式( 6 )變形可知，混凝土總應變可分解為彈性應變εe(t)和徐變應變εc(t)，即

ε(t)=εe(t)+εc(t)

( 7 )

式中：

( 8 )

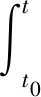
( 9 )

將連續的作用時間劃分為Δt1，Δt2，Δt3，…,Δtn等一系列時段，當Δtn充分小時，利用積分中值定理可計算每個時段的彈性應變增量和徐變應變增量，分別為

(10)

(11)

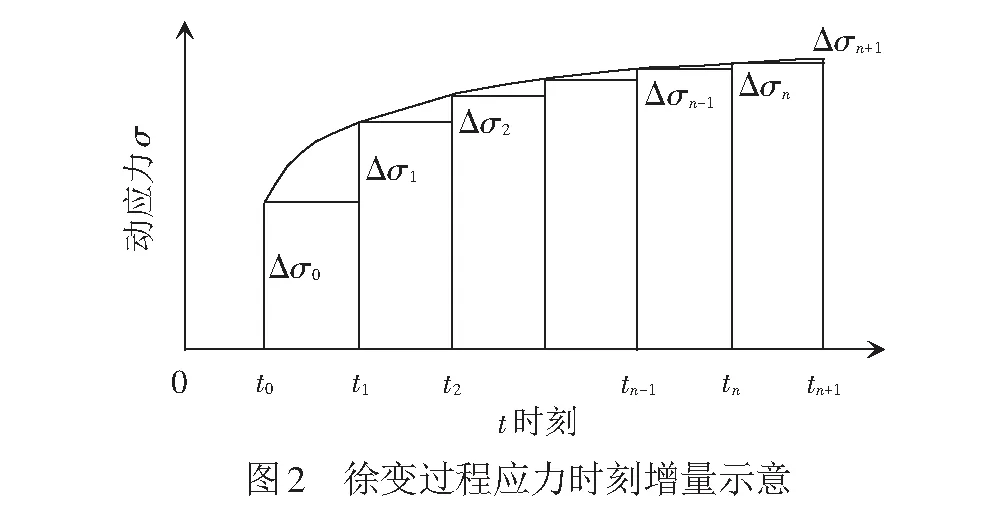
徐變過程中應力變化過程見圖2，各時刻的應力可看作該時刻前各時刻應力增量的疊加。其中，tn、tn+1時刻的徐變應變為

εc(tn)=C(tn,t0)Δσ0+C(tn,t1-0.5)Δσ1+…+

C(tn,tn-1-0.5)Δσn-1+C(tn,tn-0.5)Δσn

(12)

εc(tn+1)=C(tn+1,t0)Δσ0+C(tn+1,t1-0.5)Δσ1+…+

C(tn+1,tn-1-0.5)Δσn-1+C(tn+1,tn-0.5)Δσn+

C(tn+1,tn+1-0.5)Δσn+1

(13)

將式(13)與式(12)聯立，可得

[C(tn+1,t1-0.5)-C(tn,t1-0.5)]Δσ1+…+

[C(tn+1,tn-1-0.5)-C(tn,tn-1-0.5)]Δσn-1+

[C(tn+1,tn-0.5)-C(tn,tn-0.5)]Δσn+

C(tn+1,tn+1-0.5)Δσn+1

(14)

考慮式(14)的特點，選取指數函數型的朱氏徐變度公式，即

C(t,t0)=∑φj(t0)[1-e-rj(t-t0)]

(15)

式中：φj(t0)為與齡期t0相關的函數，可根據徐變試驗獲得。

本文采用文獻[10]中的推薦公式

將式(15)代入式(14)，可得

C(tn+1,tn+1-0.5)Δσn+1

(16)

式中：

ωj,n+1=Δσ0φj(t0)e-rj(tn-t0)+

Δσ1φj(t1-0.5)e-rj(tn-t1-0.5)+…+

Δσn-1φj(tn-1-0.5)e-rj(tn-tn-1-0.5)+

Δσnφj(tn-0.5)e-rj(tn-tn-0.5)=

ωj,ne-rjΔtn+Δσnφj(tn-0.5)e-0.5rjΔtn

(17)

ωj,1=Δσ0φj(t0)

(18)

(19)

將(16)應用到復雜應力狀態，可得

(20)

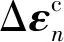
由式(11)可知

(21)

式中：B為彈性泊松比影響矩陣。

將式(20)代入式(21)，可得

Δσn=E(tn-0.5)B-1(Δεn-ηn-qnAΔσn)

(22)

由式(22)變形，可得

Δσn=

{I+E(tn-0.5)B-1Aqn}-1B-1E(tn-0.5)(Δεn-ηn)=

{B+E(tn-0.5)Aqn}-1E(tn-0.5)(Δεn-ηn)

(23)

式(23)為考慮徐變特性的混凝土本構關系。將此映射關系施加到Ansys分析模型中，就能對鋼混結合段核心混凝土的徐變作用進行計算。

4 Ansys二次開發及模型的建立

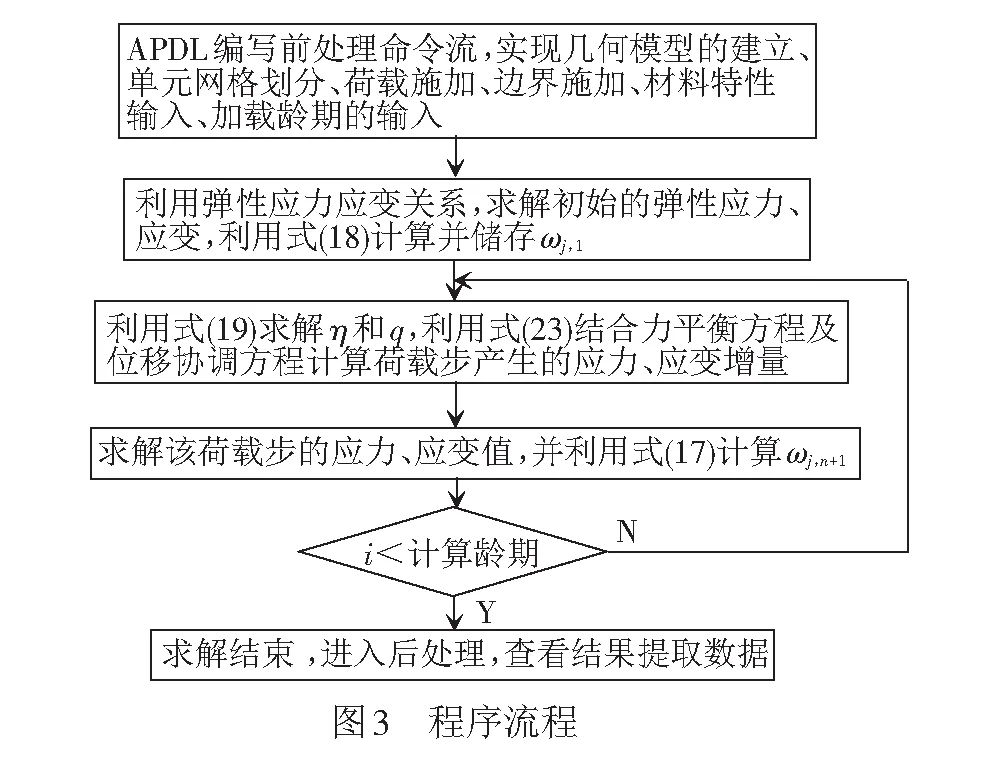
UPFS是Ansys軟件常見的二次開發工具，具有用戶可編程的屬性。用戶可運用Fortran語言對Ansys子程序重新編譯，生成滿足用戶需要的特定版本。本文對Ansys子程序(USERMAT.F模塊)進行編譯，開發出具有徐變特性的新材料，來實現混凝土徐變作用的計算。Ansys二次開發的流程見圖3。

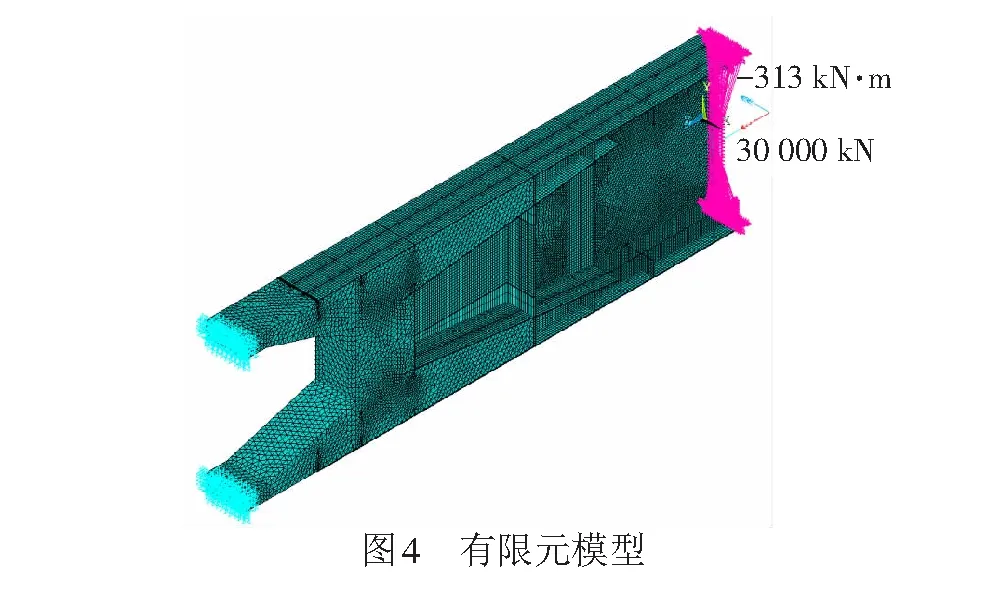
基于二次開發后的Ansys軟件建立鋼混結合段非線性局部有限元模型，采用三維實體單元Solid65模擬混凝土，通過體積配筋率考慮混凝土的配筋；采用實體單元Solid45、非線性彈簧單元Combin39模擬鋼殼體和剪力連接件。通過接觸單元用Targe170單元和Conta174單元分別模擬鋼殼體內表面和混凝土外表面，兩者摩擦系數取0.2，滲透系數取0.1。混凝土選用新開發的材料本構關系；鋼殼體及連接件采用雙線性理想彈塑性本構模型，彈性模量為210 GPa，屈服應力為320 MPa。模型為懸臂狀態，混凝土梁端固定。由圣維南原理及計算結果知，至鋼混結合段處力已完成擴散，局部強度滿足要求。模型中預應力鋼筋采用Link8單元模擬，各節點與混凝土節點耦合，通過降溫的方式施加預應力。剛度過渡端面通過Cerig命令形成剛性區后外接梁單元，第1荷載步在梁單元端部以節點集中荷載的形式分100個子步施加，最大軸向荷載為30 000 kN，彎矩為-313 kN·m；第2荷載步施加徐變荷載，徐變時間為3 650 d，分365個子步施加。有限元模型見圖4。

5 收縮徐變對鋼混結合段受力的影響

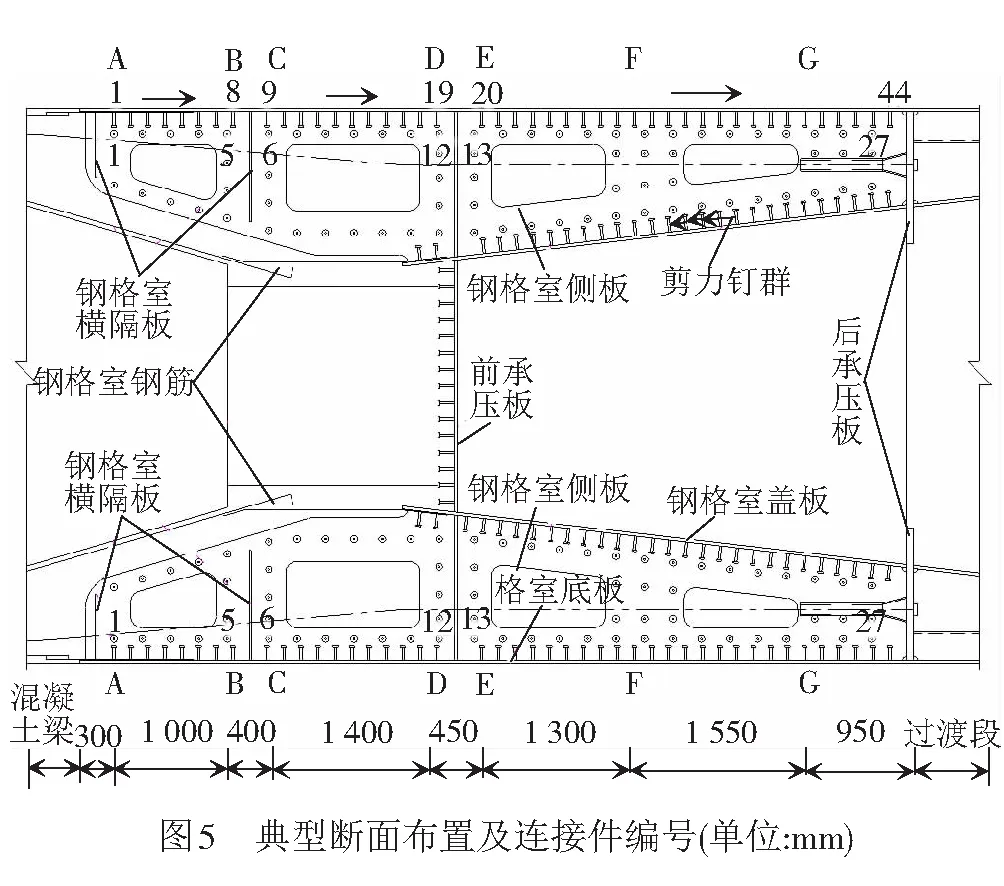
由文獻[9]可知，在鋼混結合斷面最大負彎矩工況作用下鋼混結合段受力最不利，因此本文只研究此工況下收縮對鋼混結合段應力分布和傳力機制的影響。計算徐變時，僅考慮加載齡期7 d恒載工況作用下的瞬時效應與10年徐變效應，對比分析混凝土長期徐變作用對鋼混結合段的影響。鋼混結合段典型斷面布置及剪力連接件編號見圖5。

5.1 收縮對鋼混結合段受力的影響

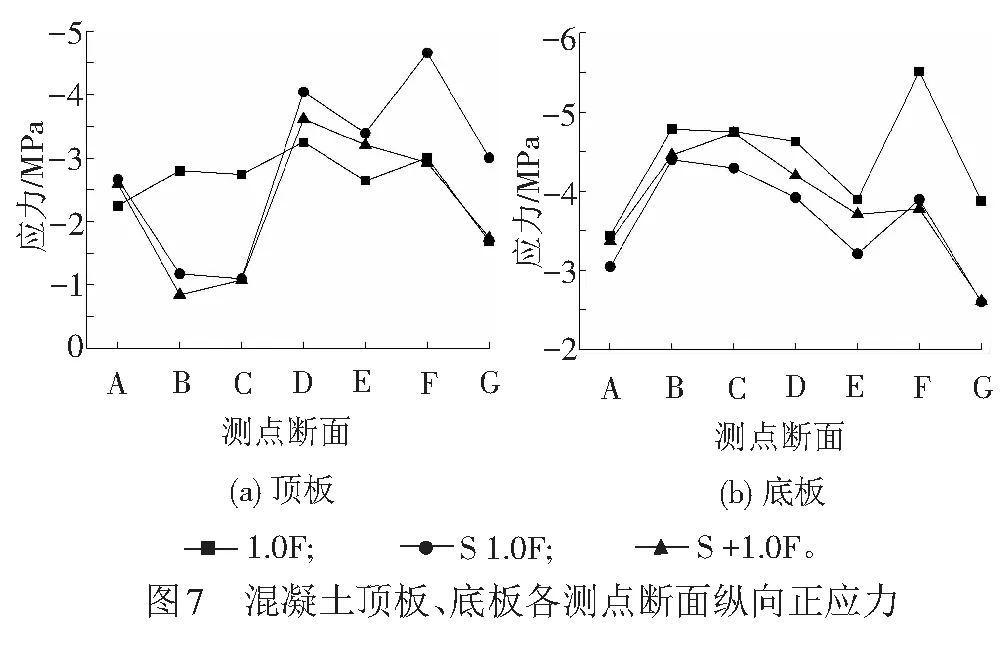
繪制最大負彎矩工況下預應力、外荷載、收縮共同作用下鋼混結合段各典型測點斷面的縱向平均正應力圖，見圖6、圖7。圖6、圖7數值中負值為壓應力，正值為拉應力。1.0F表示預應力、外荷載共同作用的結果；S1.0F表示預應力、外荷載、收縮共同作用的結果；S+1.0F表示預應力、外荷載共同作用結果與收縮作用結果的線性疊加。

由圖6可知，不考慮收縮作用(1.0F工況)鋼頂板測點應力范圍為-10.6～-24.6 MPa，鋼底板應力范圍為-14.5～-30.0 MPa，底板壓應力略高于頂板；兩端斷面(G—F、B—A)應力變化顯著，中間斷面(F—B)應力變化相對平緩，G斷面應力小于F斷面。這是由于后承壓板將鋼箱梁受到的大部分力傳遞給混凝土梁，短距離內應力未完全擴散，造成后承壓板附近的混凝土應力集中，鋼箱梁應力偏低。B—A斷面應力變化顯著，主要是由于端部鋼殼體和混凝土間的滑移量最大，剪力連接件傳力作用顯著。

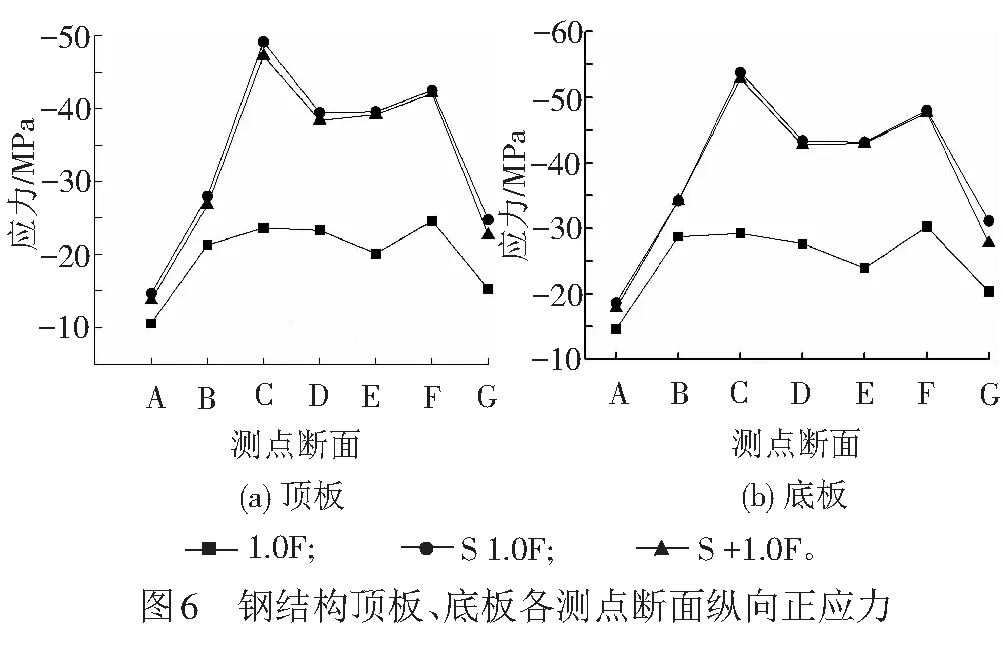
對比1.0F工況和S1.0F、S+1.0F工況可知，考慮收縮作用后各斷面平均應力顯著增大，其中C斷面鋼頂板縱向正應力由23 MPa變化至50 MPa，增加了117.4%，鋼底板縱向正應力由29 MPa變化至54 MPa，增加了86.2%，由此可知收縮作用對鋼結構應力影響更為突出。對比S1.0F與S+1.0F的應力結果可知最大應力差出現在F斷面，差值為5 MPa；其他各斷面應力差別甚微，這表明由收縮作用引起的邊界非線性并不明顯。

由圖7可知，不考慮收縮作用(1.0F工況)時，除兩端斷面外混凝土頂、底板的正應力變化均較為平緩。G—F斷面的應力變化是由后承壓板傳力導致混凝土應力集中造成的，B—A斷面的應力變化是由端部剪力連接件傳力作用造成的。

混凝土頂、底板正應力在1.0F、S1.0F、S+1.0F工況作用下的變化趨勢相似，均在G—E斷面應力突變，應力均表現為先增加后急劇降低；收縮作用對混凝土應力分布影響明顯，尤其是B、C斷面，考慮收縮后，B、C斷面頂板應力由2.5 MPa變化為1.0 MPa，減小幅度為60%。

比較1.0F、S1.0F及S+1.0F工況下1～44號栓釘、1～27號貫穿鋼筋(編號見圖5)的受力狀況，見圖8。

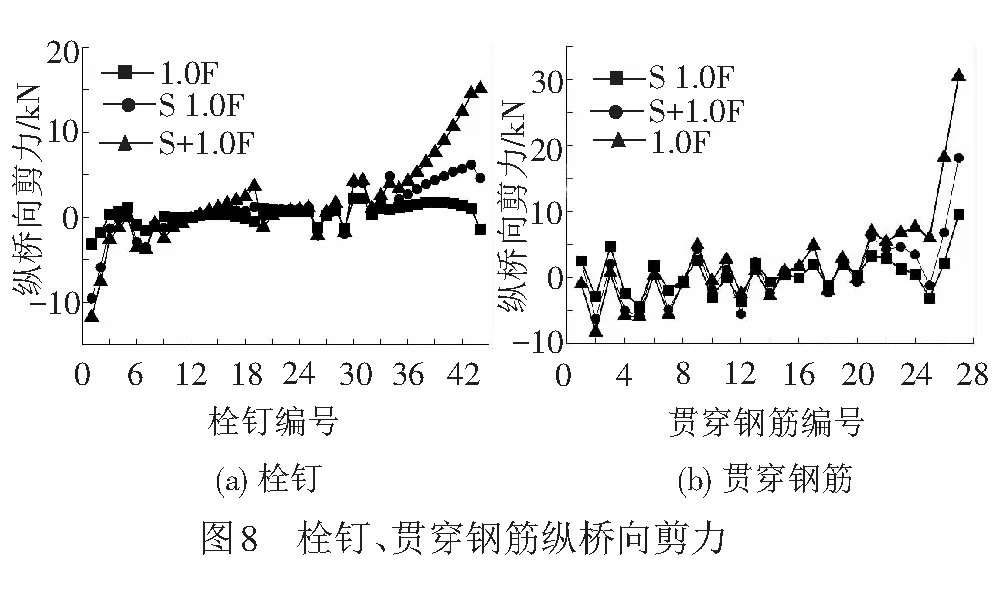
由圖8可知，收縮作用對鋼混結合段兩端剪力連接件的受力影響顯著。在靠近后承壓板處栓釘承受的剪力由-1.2 kN變成4 kN；貫穿鋼筋承受的剪力由10 kN變成17.5 kN，變化幅度為75.0%。比較S+1.0F和S1.0F的結果可知，收縮作用同樣會造成后承壓板的脫空，這種邊界非線性會改變剪力的大小、方向。

5.2 徐變作用對鋼混結合段受力的影響

由文獻[9]分析知，徐變前期變形很快，尤其是前15 d近似呈線性變化，在計算齡期為23 d時，徐變變形占10年徐變總變形的56.7%，徐變3年變形已基本達到穩定。本文提取鋼混結合段典型斷面的鋼、混凝土頂板、底板及腹板各測點的縱橋向瞬時正應力和考慮3年徐變后的正應力進行對比分析，其中鋼、混凝土頂板對比結果見圖9。經分析可得腹板、底板的應力分布規律與頂板基本相同，此處不再闡述。

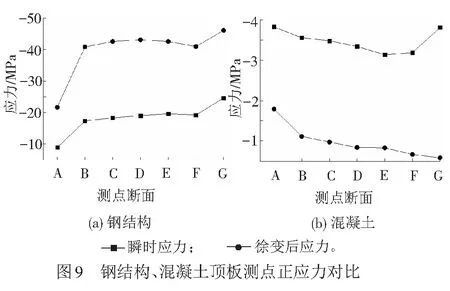
由圖9(a)可知，鋼結構頂板沿縱橋向各斷面間的瞬時應力與徐變后的應力變化趨勢類似。A—B斷面應力顯著升高，B—F斷面應力近似維持定值，F—G斷面應力再次升高。該應力變化規律表明鋼混結合段兩端剪力連接件傳力作用明顯。對比各測點斷面的應力數值可知鋼結構頂板徐變后應力最大值約是瞬時應力的2.35倍。

由圖9(b)可知，混凝土頂板各斷面間應力的變化規律與鋼結構基本相同，但應力數值較低，瞬時應力為3.25～3.80 MPa，徐變后應力為0.6～1.8 MPa。除個別點外，混凝土頂板徐變后應力最大值約是瞬時應力的0.45倍。

研究表明徐變作用同樣會影響剪力連接件的受力，其對頂板、底板和腹板產生的影響規律基本一致，在此僅列舉徐變前后頂板栓釘縱橋向剪力數值的變化，見圖10。

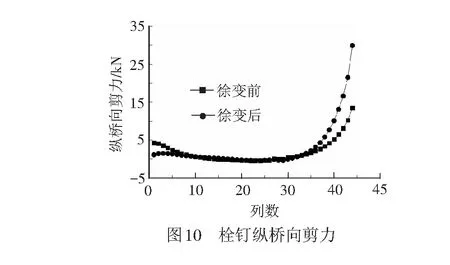
由圖10可知，栓釘承受的剪力較小，集中在2 kN以內。徐變前、后栓釘縱橋向的剪力變化趨勢近似相同，但考慮徐變后栓釘的剪力值均增大，其中后承壓板處栓釘的剪力值由徐變前的12 kN變化到徐變后的30 kN，增大了150%，但各栓釘的受力仍遠小于其抗剪極限承載力，表明考慮徐變作用后該結構仍具有較大的承載力安全儲備。

6 收縮徐變對鋼混結合段傳力的影響

上述研究結果表明收縮、徐變作用會造成鋼殼體與核心混凝土產生脫空現象和應力重分布，進而導致鋼混結合段的傳力規律及傳力機制顯著變化。提取各測點斷面的應力進行積分可獲得各截面內力，運用式( 1 )—式( 5 )計算鋼混結合段考慮收縮作用、不考慮收縮作用和考慮徐變作用、不考慮徐變作用下的軸力傳遞指標，并繪制各傳力曲線，見圖11。

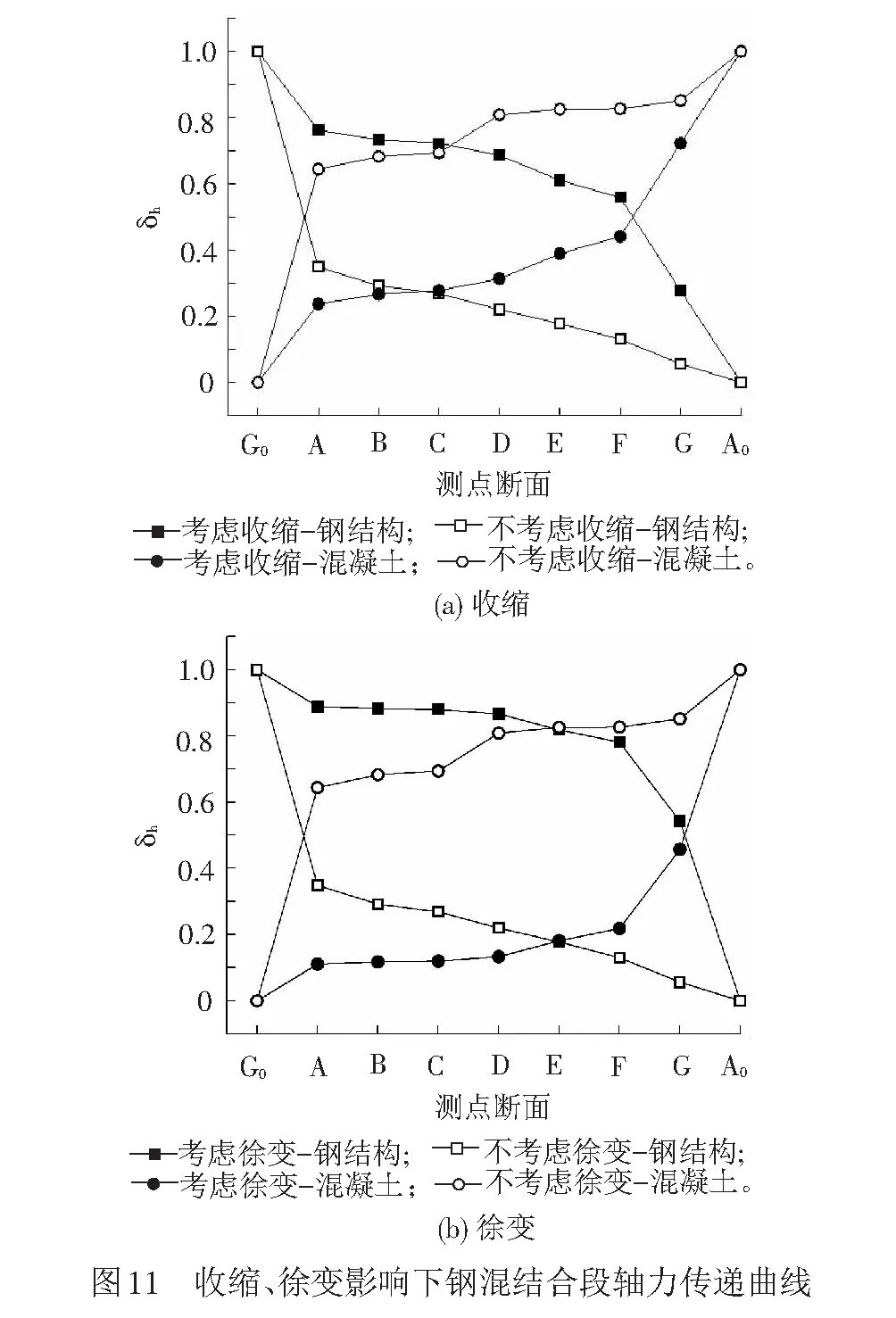
圖11中A0、G0分別為混凝土斷面、剛度過渡段斷面。由圖11(a)可知，考慮收縮作用后，后承壓板傳力率δh由58.50%減小至20.80%，傳力平均斜率α由11.27%增大至19.20%，傳力最大斜率αmax由49.33%增大至92.44%，傳力均勻度δ由0.18增大為0.31。這說明收縮作用顯著降低了承壓板的傳力作用，剪力連接件的傳力作用增強。

由圖11(b)可知，考慮徐變作用后，后承壓板傳力率δh由58.5%銳減至9.73%，傳力平均斜率α由11.27%增大至27.86%，傳力最大斜率αmax由49.33%增大至180.89%，傳力均勻度δ由0.18變為0.62。這說明考慮徐變后承壓板的傳力作用降低幅度更大；兩端剪力連接件受力更為顯著，傳力作用增強，因此鋼混結合段整體受力狀況更為不利。

7 結論

(1) 基于彈性徐變理論選取合適的指數型徐變度，可推導出不同徐變泊松比下復雜應力空間的混凝土徐變本構關系。根據此關系利用Fortran語言對Ansys中的材料本構關系進行二次開發，可實現對鋼混結合段核心混凝土的徐變計算。

(2) 收縮作用對鋼混結合段受力狀況影響顯著。其中鋼結構壓應力增大一倍，混凝土應力減小一半；剪力連接件承受的剪力增大，尤其是后承壓板附近，增大幅度為75%。

(3) 徐變作用將引起鋼混結合段的內力重分布。其中鋼殼體壓應力顯著增加，徐變3年后的應力約是瞬時應力的1.9～2.47倍；而核心混凝土徐變3年后的應力約是瞬時應力的0.13倍。

(4) 收縮、徐變作用均顯著改變了鋼混結合段的傳力模式。傳力不均勻度分別提高了0.13、0.44；鋼混結合段端部連接件承受的剪力變化幅度最大，分別增加了75%、150%。