考慮相鄰出發列車車流分配的車輛集編排隊系統分析
李 靜,帥 斌,許旻昊,朱偉波,何春燕
(西南交通大學 交通運輸與物流學院, 四川 成都 610031)
編組站是鐵路運輸的節點,有調中轉車在編組站的集結過程是不可避免且耗時較長的技術作業環節。車輛集結結束條件與集結模式有關。傳統集結模式包括定點集結和定編集結兩種。對于定點集結模式,列車完全按圖行車,只要確定發車時刻,編組結束時刻即可確定,出發條件對列車最小編成輛數沒有限制;對于定編集結模式,只要編成輛數達到滿軸編成輛數,則認為該集結過程結束。放寬條件定點集結模式是定點集結模式的過渡形式。該模式下,在編發時刻,如果集結車輛數不能滿足滿軸要求,但只要滿足最小編成輛數約束,列車也可以正點出發。放寬條件定點集結模式同時考慮“按圖行車”與列車最小編成輛數兩個約束,與傳統定點集結模式相比,增加了編成輛數約束,減少機車和區段能力浪費;與傳統定編集結模式相比,提高了列車正點發車率,運輸時效性得到改善,減少了車輛積壓。基于以上特點,放寬條件定點集結模式比傳統定點集結模式在實際生產中更容易付諸實踐[1],對提高鐵路運輸組織靈活性、時效性和便捷性具有重要意義。
集結車輛到達調車場等待編發,該過程具有排隊系統的一般特征,可以通過建立排隊模型對車輛集結過程進行分析。關于車輛集編排隊系統的研究,以往研究主要集中在傳統的定點和定編兩種模式[2-6],對放寬條件定點集結模式研究較少[7-8]。Petersen[2-3]建立了定點與定編集結模式下車輛單個到達成批服務的集編排隊系統。Turnquist等[4]在此基礎上,根據集結模式特點的不同,分別建立了兩種車輛批量服務排隊模型,并對列車編成輛數大小不作限制,這與實際不符。史峰等[5]建立了定編集結模式下車輛成批到達成批瞬時服務的隨機服務系統,集結車輛數一旦達到滿軸編成輛數,系統立馬開始服務,服務時間為0。林楓[6]分別針對定點和定編兩種集編系統建立了車輛批到達批服務排隊模型。李靜等[7-8]建立了放寬條件定點集結模式下車輛集編系統的批到達批服務排隊模型。
以上研究沒有考慮在放寬條件定點集結模式下,對相鄰出發列車進行車流分配的情形。即考慮到同一去向后編列車可能丟線,先編列車在滿足出發條件基礎上,將部分本應隨先編列車出發的車輛編組到后編列車,使得后編列車剛好滿足出發條件,以保證兩列車均正點出發[1]。針對該問題,本文構建了考慮相鄰出發列車車流分配的車輛集編排隊模型。首先,利用嵌入式馬爾可夫鏈方法求得系統在發車時刻的車輛集結隊長穩態分布,然后通過補充變量法得到系統在任意時刻隊長穩態分布與發車時刻穩態分布的關系式,并對車輛平均集結隊長、平均集結延誤時間等系統指標進行分析,重點分析車流分配對系統性能的影響。
1 系統模型
1.1 模型說明
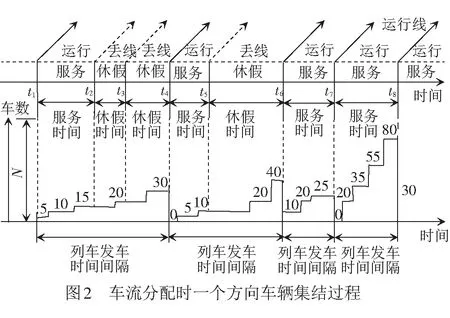
針對一個方向的車輛集編排隊系統,將其抽象描述為由該方向集結車輛和相應列車編發系統組成的單隊列單服務臺排隊模型。其中,“顧客”為集結車輛,“服務臺”為列車編發系統。假設時間軸被分成等長時間段,稱為時隙。不失一般性,時隙用0,1,2,…,t,…表示,則時間用時隙數表示。t-為車輛到達前時刻;t+為車輛離去時刻;*為任意時刻。為明確t時刻系統狀態,約定車輛到達只能發生在時隙末端(t-,t),同時約定車輛離開,即系統服務開始或結束,只能發生在時隙首端(t,t+),車輛到達時刻示意見圖1。本文排隊模型采用具有延遲入口的晚到系統[9]。

一般來講,系統狀態概率在到達前時刻,離去時刻與任意時刻是不相等的。
1.2 模型構建
(1) 到達過程
車輛以車組的形式批量到達,假設車組到達為Bernoulli過程,離散時間的Bernoulli到達過程相當于連續時間的Poisson過程[2,4,6,10-11],具有與Poisson到達過程一樣的無后效性[12]。λ為車組到達強度,0<λ<1;X為1次到達車組包含車輛數,為正整數隨機變量。其分布函數及母函數分別為
gm=P(X=m)m≥1

(2) 服務過程
列車圖定發車時刻表已知,當不考慮調機運用及出發作業能力限制時,車輛在集編系統延誤時間主要由等待出發時刻造成[4]。因此,假定最晚編組時刻與列車圖定發車時刻之間的編組及出發作業時間為固定值[13],則列車圖定發車時間間隔與最晚編組時間間隔具有相同的分布規律。為討論方便,在文中不考慮最晚編組時刻與列車出發時刻之間的固定時間,將最晚編組時刻稱為發車時刻,并將間隔時間用排隊理論中的專門用語“服務時間”描述。
由此,定義從列車出發時刻起到下一個發車時刻之間的過程為排隊系統的服務過程,服務過程持續時間為服務時間,也稱為車輛集編排隊系統處于運行期間。時刻t1與t2之間的過程為系統服務過程,見圖2。S為服務時間,其概率分布st為
st=P(s=t)t=1,2,3,…
母函數S(z)為
假設系統服務時間與服務批量大小無關。系統運行結束只能發生在時隙首端(t,t+)期間內,此時,t+也稱為系統運行結束時刻。
(3) 休假過程
在發車時刻,如果集結車輛數不能滿足最小編成輛數約束,列車不能組織編發。如圖2中,最小編成輛數l為25,滿軸編成輛數c為50,t2時刻系統內集結車輛數為15,小于最小編成輛數,該情形下,列車丟線,車輛繼續集結,等待下一條運行線。從列車丟線時刻起到下一個出發時刻為止之間的過程稱為排隊系統的休假過程,也稱為車輛集編排隊系統處于丟線期間。如時刻t2與t3之間的過程為系統休假過程。V為休假時間,其概率分布vt為
vt=P(v=t)t=1,2,3,…
母函數V(z)為
當車列提前或延遲集結結束,不考慮加線。同樣系統丟線結束只能發生在時隙首端(t,t+)期間內,此時,t+稱為系統丟線結束時刻。
在發車時刻,只要系統內集結車輛數不能滿足最小編成輛數要求,列車可能多次丟線。如圖2所示,在t3時刻,系統內集結車輛數為20,還是小于最小編成輛數,在上一次丟線結束以后,列車再次丟線。
從以上描述可知,系統運行結束及系統丟線結束時刻等同于車輛離去時刻,在文中統稱為發車時刻。
(4) 排隊規則
N為某集結方向最多等待車輛數,則系統內最多車輛數為N+c(c≤N),并假設當容量限制時,到達車組可以拆分,即部分車輛進入調車場,剩余車輛不能進入。車輛按照先到先服務的規則等待編發。
(5) 服務規則
在發車時刻,車輛集結隊長為n時,先編列車在滿足出發條件基礎上,將部分本應隨先編列車出發的車輛編組到后編列車,使得后編列車剛好滿足出發條件。服務批量大小等于列車編成輛數,該參數為同時受列車最小編成輛數與滿軸編成輛數限制的正整數隨機變量。
在發車時刻,相鄰出發列車不分配車流的情形包括:
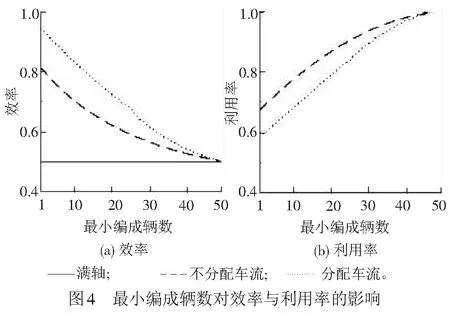
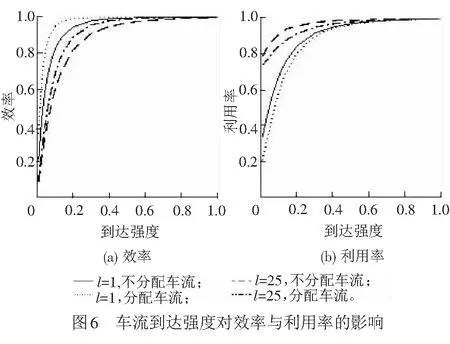
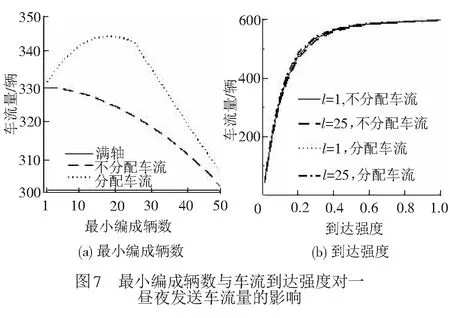
① 車輛集結隊長n ② 車輛集結隊長n=l時,組織所有車輛編發,系統進入運行過程,剩余車輛數為0,該情形下,先編列車不用為后編列車分配車流。 ③ 車輛集結隊長n滿足l+1≤n≤min(c+l-1,N)時,存在兩種情形不需要進行車流分配:一是當先編列車編成輛數為最小編成輛數l時,能為后編列車分配的最大車輛數為(n-l),當前列車出發以后,系統運行期間內到達車輛數與剩余車輛數之和仍然小于最小編成輛數,該情形下不分配車流。因為即使最大限度的為了保證兩列車均正點出發,還是不能滿足后編列車的出發要求,寧可將集結車輛編入先編列車出發,從而減少車輛集結時間。二是當先編列車滿軸出發以后,剩余車輛數與當前列車運行期間內到達車輛數之和能夠滿足后編列車最小編成輛數約束,該情形下,先編列車不用為后編列車分配車流。 ( 1 ) 以圖2為例對上述分配車流規則進行說明。在發車時刻t2與t3處,集結車輛數均小于最小編成輛數,列車連續兩次丟線,先編列車不用為后編列車分配車流。t4時刻,車輛集結隊長為30,大于最小編成輛數,且估計到系統運行期間能夠到達的車輛數為15,先編列車最多能為后編列車分配的車輛數為5,后編列車仍然不能滿足出發條件,因此,先編列車不為后編列車分配車流,組織所有車輛編發,剩余車輛數為0。t5時刻,集結隊長為15,小于最小編成輛數,列車丟線,先編列車不用為后編列車分配車流。t6時刻車輛集結隊長為40,大于最小編成輛數,且估計到系統運行期間能夠到達的車輛數為15,為了保證后編列車也能正點出發,t6時刻,列車不全部編發所有集結車輛,而是只編組前30輛車,為后編列車留下10輛,使得后編列車也能剛好滿足出發條件。t7時刻,本應隨t6時刻列車出發的10輛集結車輛,再加上t6與t7時刻之間到達的15輛車,列車剛好能夠滿足出發條件,立即組織所有車輛編發,先編列車同樣不用為后編列車分配車流。t8時刻,系統內車輛集結隊長為80,當前列車即使滿軸編發,剩余車輛數為30,后編列車也能夠滿足出發條件,所以先編列車不用為后編列車分配車流。 假設以上隨機過程均具有平穩性與各態歷經性;在安排發車時,暫不考慮機車運用、區段通過能力和技術站作業能力的限制。 系統只有在發車時刻才具有馬爾可夫性,因此,設定發車時刻車輛集結隊長為系統狀態變量,利用嵌入式馬爾可夫鏈方法得到發車時刻系統狀態的平穩分布。對于成批到達的系統,發車時刻與任意時刻的車輛集結隊長不服從相同分布[14]。因此,為了得到任意時刻車輛集結隊長分布,需要尋求其與發車時刻隊長分布之間的關系。 式中:S為系統處于運行狀態;V為系統處于丟線狀態;矩陣SS,SV,VS,VV分別表示系統在運行和丟線兩種狀態之間轉移。根據系統描述可知:SSε=VSε,SVε=VVε。由于對相鄰出發列車進行車流分配,分配車流方案一步狀態轉移概率矩陣在不分配車流方案基礎上發生變化。發生變化情形是在發車時刻車輛集結隊長大于最小編成輛數時,即當系統狀態轉為運行狀態時,由于SS1=VS1,這里只討論SS1情形。SS0為不進行車流分配時一步狀態轉移概率矩陣,SS附加為對車流進行分配時一步狀態轉移矩陣發生的變化,兩者之和即為分配車流情形下的一步狀態轉移概率矩陣,表示為SS1=SS0+SS附加。具體計算公式為 式中: j>0k≥1 1≤n≤N-1 k≥1 0≤a≤l-1 1≤n≤N-1-a 當j+c≥2l時,δj+c=1,否則δj+c=0。 定義聯合概率 σn(r,t-)=P(Nt-=n,Rt-=r,εt-=1) 0≤n≤Nr≥0 ωn(r,t-)=P(Nt-=n,Ht-=r,εt-=0) 0≤n≤Nr≥0 穩態條件下有 σn(r)=limt-→∞σn(r,t-) ωn(r)=limt-→∞ωn(r,t-) 對應母函數分別為 |z|≤1 0≤n≤N 當l ( 2 ) ( 3 ) (1-λ)[σc+n(0)+ωc+n(0)]l+1≤n≤N-c-1 ( 4 ) ( 5 ) ( 6 ) 當l≥N-c時 ( 7 ) ( 8 ) ( 9 ) (10) (11) ω0=(1-λ)ω0-(1-λ)ω0(0)+(1-λ)[σ0(0)+ω0(0)] (12) (13) (14) (15) (16) (17) 式中:E(S)、E(V)分別為平均服務時間、均值。 由式( 2 )~式(17)可求得{σn,ωn}。 (1) 車輛平均集結隊長 系統任意時刻車輛集結隊長為n的概率pn為 pn=σn+ωn0≤n≤N 則車輛平均集結隊長Lq為 (18) (2) 車輛平均集結延誤時間 Wq為車輛平均集結延誤時間,表示任意待集結車輛在編發系統內集結等待的平均時間。由于車輛平均集結延誤時間與平均集結隊長之間滿足Little關系,因此,車輛平均集結延誤時間為 (19) (3) 效率 用任意時刻系統處于運行過程概率來反映編發系統工作效率,則編發系統處于忙期概率ρb為 (20) (4) 利用率 列車牽引能力利用率p利用率為列車平均編成輛數與滿軸編成輛數的比值,則 p利用率=Ls/c (21) (5) 一晝夜發送車流量 E為一個方向車輛集編排隊系統一晝夜服務完成后離開的車輛數為一晝夜發送車流量 E=n圖×ρb×Ls (22) 式中:n圖為該方向一晝夜圖定平均發送列車數,n圖=24/E(S)。 車流到達強度λ=0.1時,分配車流方案的車輛平均集結隊長與集結延誤時間均隨著最小編成輛數增加而先減小后增大,不分配車流方案的車輛平均集結隊長與集結延誤時間均隨著最小編成輛數增加而單調遞增,見圖3。分配車流方案車輛平均集結隊長和集結時間均大于不分配車流方案,在最小編成輛數較大時,甚至大于采用滿軸編成輛數時集結隊長和時間,因此,從節省車輛集結時間角度,對相鄰出發列車進行車流分配是不利的。 最小編成輛數對效率與利用率的影響見圖4。由圖4可見,編發系統工作效率隨著最小編成輛數增加逐漸下降,利用率逐漸上升,分配車流方案效率高于不分配車流方案,但利用率低于不分配車流方案,表明對相鄰出發列車進行車流分配增加了列車正點發車概率,但出發列車平均編成輛數會有所下降。 當最小編成輛數l分別為1、25時,車輛平均集結隊長與集結延誤時間隨車流到達強度變化的趨勢,見圖5。由圖5(a)可見,隨著車流到達強度增加,車輛平均集結隊長增加,但分配車流方案集結隊長大于不分配車流方案;由圖5(b)可見,當l=1時,即在定點集結模式下,分配車流方案的車輛平均集結延誤時間隨著車流到達強度增加而先增加后減小并逐漸趨近于平穩。可以解釋為,當車流到達強度較小時,本應隨先編列車出發的車輛為了等待后編列車而增加了延誤時間;當車流到達強度繼續增大,該類延誤時間減小,車輛平均集結延誤時間呈現下降趨勢;隨著到達強度繼續增大,車輛需要在站集結等待列車運行時刻,且由于容量限制,超過容量限制的車輛不能進入系統,車輛集結延誤時間逐漸趨近于平穩。當l=25時,分配車輛方案車輛集結延誤時間隨車流到達強度增加而先減小后增大直至趨近平穩,分配車輛方案與不分配車流方案車輛集結延誤時間隨車流到達強度具相似的變化趨勢。但分配車流方案車輛集結延誤時間始終大于不分配車流方案。 車流到達強度對效率與利用率的影響見圖6。由圖6(a)可見,車流到達強度越大,列車出發運行的概率越高,編發系統的工作效率越高,分配車流方案效率高于不分配車流方案;圖6(b)表明車流到達強度越大,列車平均編成輛數越大,列車牽引能力利用率越高,分配車流方案能力利用率小于不分配車流方案,隨著到達強度增加,分配車流方案和不分配車流方案的利用率均趨近于1。 當λ=0.1時,一晝夜發送車流量受到最小編成輛數變化的影響見圖7(a)。最小編成輛數與不分配車流方案一晝夜發送車流量呈負相關,即最小編成輛數等于1時,該方向一晝夜發送車流量最多。分配車流方案一晝夜發送車流量隨著最小編成輛數增加而先增加后減小,最小編成輛數較小時,車流分配增加了列車發車概率,運行線能力較不分配車流方案得到了更好利用;但隨著最小編成輛數增大,列車丟線概率增加,丟線導致發送車流量下降。分配車流方案一晝夜發送車流量大于不分配車流方案。同時,隨著到達強度增大,分配車流方案與不分配車流方案的發送車流量均呈現增長趨勢,兩者變化規律基本一致,見圖7(b)。 定義最優最小編成輛數為使得該方向一晝夜發送車流量最大的最小編成輛數。當不分配車流時,最優最小編成輛數始終等于1,見圖7(a)。當分配車流時,最優最小編成輛數及對應列車平均編成輛數和平均集結隊長變化趨勢見圖8。隨著到達強度增加,最優最小編成輛數增加,到達強度較小時,最優最小編成輛數增長較快,到達強度較大時,增長趨于平穩。該算例中到達強度在[0.25,0.81]區間變化時,最優最小編成輛數恒為25。車輛平均集結隊長和列車平均編成輛數隨著車流到達強度增加而增加,當到達強度足夠大時,列車平均編成輛數基本等于滿軸編成輛數,車輛平均集結隊長逐漸增大并逐漸趨近系統容量限制。 本文將車輛在站集結過程描述成具有容量限制的采用多重休假策略的批到達批服務離散時間排隊模型。考慮相鄰出發列車車流分配,引入了車流分配機制,得到了穩態條件下發車時刻及任意時刻車輛集結隊長分布,并得到了系統指標的數學表達式。最后,通過算例,針對分配車流方案與不分配車流方案的系統指標及最優最小編成輛數變化規律進行了對比分析。 算例結果表明:(1)分配車流方案較不分配車方案,車輛的平均集結隊長與平均集結延誤時間均較長,從減少車輛集結延誤時間角度,對相鄰出發列車進行車流分配是不利的。(2)對相鄰出發列車進行車流分配使得列車平均編成輛數減小,但由于提高了發車時刻列車正點發車概率,綜合起來表現為分配車流方案一晝夜發送車流量較大。因此,從增加一晝夜發送車流量角度,對相鄰出發列車進行車流分配是有利的。(3)分配車流方案的最優最小編成輛數隨著到達強度增加而逐漸增大,不分配車流方案的最優最小編成輛數則始終等于1。
2 系統穩態分布
2.1 發車時刻車輛集結隊長分布
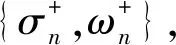
2.2 任意時刻車輛集結隊長分布
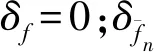
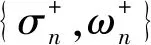

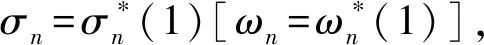

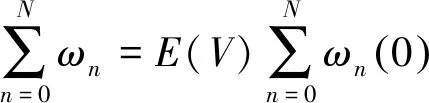
3 系統性能指標

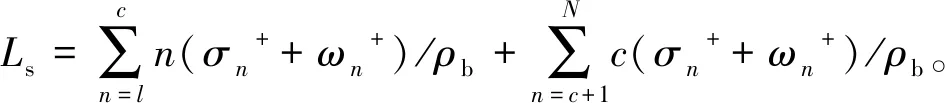
4 算例分析




5 結束語

