高考數學能力小題訓練（3）

一、填空題

1.設 集 合M = ｛x|x2=x｝，N =｛x|lgx≤0｝，則M∩N=

2.（2020年合肥第一次教學質量檢測）已知直線2x-y+1=0與曲線y=aex+x相切（其中e為自然對數的底數），則實數a 的值是

3.已知函數f（x）=2ax2+4（a-3）x+5在區間（-∞，3）上是減函數，則a的取值范圍是

4.在各項均為正數的等比數列｛an｝中，若a2=2，則a1+2a3的最小值是

6.將一顆質地均勻的骰子（一種各個面分別標有1，2，3，4，5，6個點的正方體玩具）先后拋擲兩次，則出現向上的點數之和為3的倍數的概率為

7.按右圖所示的程序框圖運算，若輸入x=17，則輸出的x值是

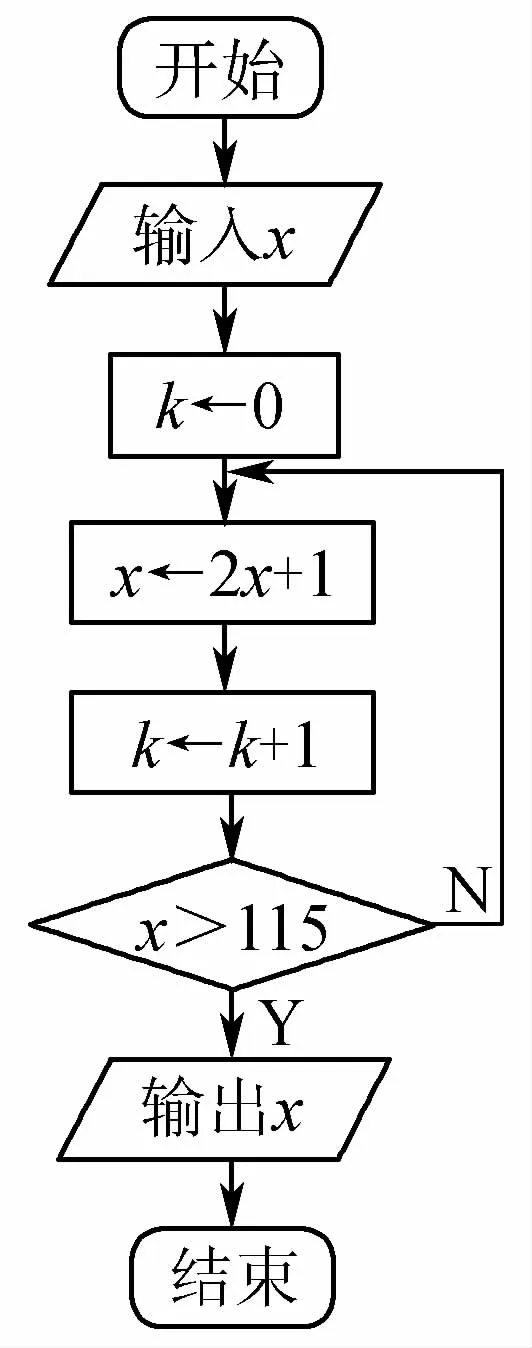
（第7題）

8.設F1，F2分別是雙曲線的左、右焦點，若雙曲線上存在點A，使∠F1AF2=90°，且AF1=3AF2，則雙曲線的離心率為

9.已知圓錐的底面半徑與球的半徑都是1cm，如果圓錐的體積與球的體積恰好也相等，那么這個圓錐的側面積是cm2.

若z的最大值為6，則z 的最小11.設z=x+y，其中實數x，y 滿足值為.

13.已 知A，B 為 圓C：（x-m）2+（y-n）2=9（m，n∈R）上兩個不同的點（C 為圓心），且滿足，則|AB|=

14.設函數f（x）=min｛x2-1，x+1，-x+1｝，其中min｛x，y，z｝表示x，y，z中的最小者.若f（a+2）＞f（a），則實數a的取值范圍為

二、解4題

15.（2020年成都質檢）如圖，在平面匹邊形ABCD 中，AB⊥BC，AB=2，BD=∠BCD=2∠ABD，△ABD 的面積為2.

（1）求AD 的長；

（2）求△CBD 的面積.

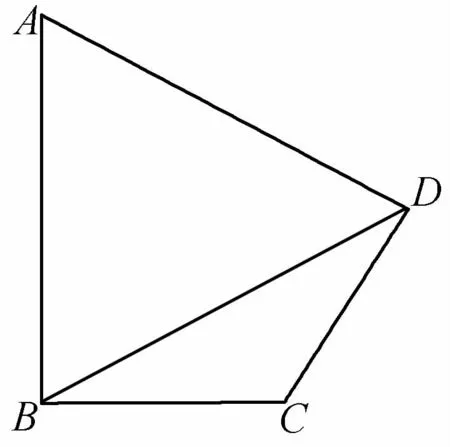
（第15題）

（1）求證：AB∥EF；

（2）若PA=AD，且平面PAD⊥平面ABCD，試證明：AF⊥平面PCD.

（第16題）