基于數學認知結構的復習課特點解析

摘? ?要? ?學生建構科學合理的數學認知結構是數學教學的出發點與落腳點。復習課是數學教學的常見課型，通過復習，要優化學生的數學認知結構，使學生的數學認知結構更加科學合理，提高學生數學認知能力。本文基于數學認知結構視角，從數學認知結構的完備性、重構性、網絡性、寬深性四個方面，談談在復習課中優化學生的數學認知結構。

關鍵詞? ?數學認知結構? 完備性? 重構性? 網絡性? 寬深性

復習課是以鞏固梳理已學過的知識、技能為主要任務，以促進知識系統化、形成科學合理的認知結構為核心，以提高發現問題、提出問題、分析問題、解決問題能力為最終目標的一種課型[1]。復習課是對已學內容的再回顧、再組織、再應用和再反思，其區別于新授課的顯著特征是復習課具有重復性、概括性、系統性、綜合性和反思性[2]。有效的復習課，有利于學生完善基礎知識表征，有利于學生形成基本技能程序，有利于學生建構良好的策略性知識，從而使學生形成科學合理的認知結構，因此復習課受教師的高度重視。基于數學認知結構的復習課有以下幾個特點。

一、完備性

完備性是指學生的數學認知結構的完整性與正確性。數學認知結構本質是學生長時記憶中數學知識的總和，是由知識之間的內在聯系、認知者的自我組織等形成的知識網絡結構[3]。這個結構是因人而異的：一是因為不同的人，表征數學知識的能力、形式、習慣是不同的，二是認知結構的差異性，也會導致數學認知結構的差異性。在復習課上，教師要有目的地安排復習課的內容，其中重要的一點就是要發現學生的數學認知結構的不完備的地方，然后，有目的地進行復習課教學。

首先，發現學生認知結構錯誤，及時修正。如（a+b）2=a2+b2，因為學生在學習完全平方公式前，學習了（ab）2=a2b2，學生把（a+b）2納入了（ab）2=a2b2的結構，所以出現了如此錯誤。造成此錯誤的根本原因是學生沒有仔細區別兩個整式，式子（ab）2=a2b2，a與b之間是乘法，而式子（a+b）2=a2+b2，a與b之間是加法。因此要通過復習，糾正學生的錯誤，使學生形成正確的認知結構。其次，發現學生數學認知結構中知識有遺漏，及時補上。如在平面幾何教學中，教師要總結證明兩直線平行的方法，若發現學生認知結構中沒有或缺少這一知識，要在復習課中及時補上，確保認知結構完備性。最后，發現學生認知結構中程序性知識與過程性知識銜接有斷裂，及時彌補。學生雖然在數學認知結構中有了陳述性知識，但沒有運用知識去解決問題，也就是程序性知識沒有形成。學生在解決實際問題的過程中，沒有自己的體驗，過程性知識沒有形成。如等腰三角形的三線合一定理，很多學生知道這個定理但不會使用，數學認知結構中只有陳述性知識，程序性知識沒有形成。通過復習課教學，要使學生在某一知識上保持完備性，對這類知識要進行復習，使學生具有陳述性知識、程序性知識、過程性知識。

二、重構性

重構性是指通過復習，學生可調整原有的數學認知結構，使之更科學合理。教師在數學復習課中，要把所學習的知識系統化，把學習過的知識通過一定的方式方法聯系起來，這樣學生就要改造原有的數學認知結構，組成新的數學認知結構，使之更加緊密合理，更容易被激活。

如學生在學習全等三角形后，在復習階段教師會對各種圖形進行充分的變式，使學生重新認識所學習過的圖形。學生原來的認知結構中是單一的圖形——基本圖形8型圖，通過對基本圖形的變式，使學生能夠充分地認識一類圖形，這時學生要重構認知結構，使認知上一個臺階。圖1、圖2兩個圖組的本質是都含有8型圖，后面的5個圖形都可看成是由8型圖演變而來，這樣，學生通過復習，其認知能力就上了一個臺階。學生可以在認知了8型圖后，將后面的圖形化為一類圖形，這樣，對認知結構進行整理，可以使認知能力得到加強。

三、網絡性

網絡性，一是通過復習使學生學過的知識網絡化，能通過超鏈接快速提取知識;二是不同的知識之間建立聯系，便于分析比較，利于模式識別。

第一，建構問題集合。華東師范大學李士锜教授認為：數學認知結構在形式上看是由節點和連線組成的復雜的網絡。節點就是結構中的元素或對象，連線則是元素間存在的穩定聯系。最基本的形式有三種：線性結構、樹型結構和網絡結構[4]。學生對學過的數學知識，依據其內部聯系會形成一個個的樹形結構，但是樹形知識結構有一個弱點，就是當需要提取數學知識時，要遍歷這棵知識樹，也就是要依據一定的順序，搜索數學認知結構，因此需要時間。如果把知識之間依據用途建立超鏈接，如同網頁中的超鏈接，一點直接就可打開要的網頁，這樣省去要遍歷這棵知識樹的時間，從而快速提取知識。如在學習平行線時，總結證明兩直線平行的方法，形成一個證明方法集合。到了平行四邊形學習后，在復習課時，再次總結證明兩直線平行的方法，把運用平行四邊形證明兩條直線平行的方法加入進來，數學認知結構中證明兩直線平行的方法就會形成新的集合，便于快速提取。第二，不同知識建立內部聯系，有利于區別，也有利于模式識別。數學知識之間是既有聯系又有區別的整體，復習課時，要把這些知識整合到一起，形成網絡模快。如函數知識與方程知識之間。把函數問題轉化為方程問題，也可把方程問題轉化為函數問題，可把這兩部分知識之間建立起聯系，這樣函數知識與方程知識之間就形成了一個更大的網絡知識模快，更有利于學生在模式識別時，區分開兩類知識，利于模式識別。

四、寬深性

寬深性是指寬度與深度。寬度一是指數學認知結構中知識點總數，二是指學生在解決一個數學問題中的知識點總數，三是學生發現問題、提出問題、分析問題、解決問題的總數。深度是數學認知結構中程序性知識的產生式序列的長度。通過復習，寬度與深度都要得到增加。

首先，提高學生數學認知結構的寬度。數學知識由三類知識構成：陳述性知識、程序性知識、過程性知識。其中程序性知識分為認知策略與智慧技能。智慧技能又分簡單操作技能與復雜操作技能。對簡單操作技能知識，學生通過認知、分解聯系階段，要在復習階段達到一定的自動化程度。對復雜操作性技能，沒有固定的方法，因此達不到自動化的程度。但這部分知識，在復習課時，教師可依據問題思維方法的共性加以抽象總結，形成一類問題的解題策略與思維方法。如在初三對拋物線中的相似三角形問題進行復習時，通過復習學生可掌握此類問題的解題策略，并且在問題的分析過程中，學生會獲得一些分析問題的體驗，感悟解題的全過程，教師可在復習過程中抽象總結出解決問題的程序。這樣，學生認知結構的寬度會有明顯增加。

其次，提高學生解決一個數學問題的寬度。解答一個數學問題所需要的知識點數量是不同的，有的數學問題解答需要的知識點單一，有的數學問題解答需要的知識點較多，通過復習，要提高學生解答數學問題的寬度。學生在解答數學問題時，雖然在數學認知結構中有所需要的知識點，但不能把這些知識點聯結起來組成程序性知識，因而解決不了數學問題。通過復習，要使學生能夠把這些知識點聯系起來解決問題，從而提高解決數學問題的寬度。

再次，提高學生發現問題、提出問題、分析問題、解決問題的寬度。復習課中要設計一些需要學生發現一定的問題才能解答的題目，這樣可激活學生的創新意識，讓學生獲得創新成功體驗。例如：在初二直角三角形性質、正比例函數、反比例函數、兩點間距離公式學完后的復習課中，給出如下例題：

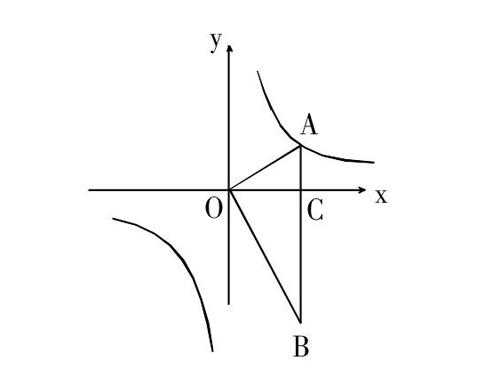
如圖3，在平面直角坐標系中，OA⊥OB，AB⊥x軸于點C，點A（■，1）在反例函數y=■的圖像上。

圖3

（1）求反比例函數y=■的表達式;

（2）求△AOB的面積;

（3）在x軸上是否存在一點P，使得以O、B、P三點為頂點的三角形是等腰三角形，若存在，請直接寫出所有符合條件的點P的坐標，若不存在，簡述你的理由。

學生要順利解答此題，在解題的過程中要發現∠AOC=30°才可以。還可給一些探究性題目，讓學生探究，提高學生分析問題解決問題的寬度。

最后，提高學生數學認知結構的深度。學生在沒有復習之前，學習的知識比較單一，并沒有把所學的知識串聯在一起解決問題，因此其程序性知識的產生式序列較短。但是當進行復習課時，會把所學知識綜合在一起解決數學問題，因而程序性知識的產生式序列長度會明顯增加。

總之，復習課教學是優化學生認知結構的好時機，教師要抓住這個寶貴時機，優化學生的認知結構，使學生的認知結構更加科學合理，從而提高學生的認知能力。

參考文獻

[1] 何善亮.復習課教學存在的問題及其改進建議[J].當代教育科學，2012（02）.

[2] 吳建新.基于有效教學的初中數學復習課策略研究[D].長春：東北師范大學，2009.

[3] 劉海濤.芻議初中生數學認知結構[J].教學導刊：上半月，2015（06）.

[4] 李士锜.PME：數學教育心理學[M].上海：華東師范大學出版社，2001.

【責任編輯? 郭振玲】