基于不同認知負荷任務的學生心理折疊水平研究

鐘 熠，謝圣英

基于不同認知負荷任務的學生心理折疊水平研究

鐘 熠，謝圣英

（湖南師范大學 數學與統計學院 計算與隨機數學教育部重點實驗室，湖南 長沙 410081）

培養學生的空間能力是數學教育的重要目標，心理折疊是空間能力的重要體現之一．研究不同認知負荷任務下學生心理折疊的認知過程，發現學生在低認知負荷任務下表現更好；在低認知負荷任務下學生表現差異與圖式自動化有關；高認知負荷任務下學生表現差異則與圖式建構相聯系；心理折疊水平可劃分為：前操作水平、單一操作水平、關聯操作水平．學生心理折疊水平的研究可幫助評價學生的數學空間能力，從而在準確把握學生已有認知水平的基礎上，開展有針對性的教學，發展學生的數學核心素養．

心理折疊；認知負荷；空間能力；數學思維

1 問題提出

心理折疊要求兒童在頭腦中將二維的空間圖形通過表象操作，轉換成三維的空間圖形[1]，是空間能力的重要體現．Milivojevic B（2003）從腦科學角度出發，解釋了心理折疊與大腦右半球有密切聯系，而大腦右半球正是空間能力的控制區域[2]．數學成績與空間能力顯著正相關[3]，更高層次的數學在本質上所需的多數思維是空間思維[4]，培養學生運用空間思維認識事物一直是數學教學的重中之重．“在數學課程中，應當注重發展學生的空間觀念”[5]“通過高中數學課程的學習，學生能發展幾何直觀和空間想象能力”[6]．空間觀念、幾何直觀、空間想象是空間能力內涵下不同層次水平的再現[7]，自1963年正式提出數學三大能力，到現在倡導發展學生的數學核心素養，如何培養學生的空間能力始終是數學教育關注的話題．

目前關于心理折疊已有許多量化研究[1，8–10]，但學生進行心理折疊任務時的認知過程分析，未有專門論述．認知負荷理論認為，學生進行認知任務時需在工作記憶中同時加工多個信息元素，有可能出現超負荷使其無法進行信息有效加工[11]，認知負荷是影響學習的重要因素．因此，研究旨在基于不同認知負荷任務分析學生心理折疊的認知過程，嘗試對心理折疊水平進行劃分，為發展學生空間能力提供幫助．

2 理論基礎

認知負荷表示處理具體任務時加在學習者認知系統上負荷的多維結構[12]，是在特定的作業時間內施加于個體工作記憶的心理活動總量[13]．以資源有限理論為基礎[14]，認知負荷理論認為個體所能承擔的認知負荷總量是固定的，只有當學習活動引起的認知負荷低于總量時有效學習才可能發生．而知識以圖式的形式儲存在個人知識結構中[15]，圖式能幫助工作記憶對加工材料進行分析，從而有效降低認知負荷[16]．

認知負荷可分為內在認知負荷和外在認知負荷[17]．外在認知負荷是由于不恰當的教學設計引起，是可以改變的認知負荷．內在認知負荷取決于所要學習的材料的本質與學習者專業知識之間的交互[12]，是不可改變的認知負荷．在學習材料不變的情況下，學習水平更高的學生受到的認知負荷會低于水平較低者．這是因為學習水平更高者能在豐富圖式的幫助下有效地降低認知負荷，而水平較低者由于沒有足夠的圖式幫助其釋放工作記憶的空間，造成認知負荷過重，從而無法完成任務．因此，學生由同一學習材料引起的實際認知負荷根據認知水平不同而有所差異，通過觀察學習者在不同認知負荷心理折疊任務下的表現，可以判斷其所在的心理折疊水平．

與心理折疊相關的研究主要有兩方面：一是說明其與空間能力的關系[18–19]；二是常將其作為考察學生空間能力的子測試．此類研究源于心理學領域，研究對象多為兒童[1，20]．首都師范大學連四清、周珍等人在此基礎上，對研究設計進一步修改，對中學生空間認知能力進行了研究[8–9，21–22]．周江霞進一步拓展，考慮不同認知方式對空間認知能力的影響[10，23]．研究皆以測試作為主要手段，通過統計方法量化分析．測試分數可作為判定知識水平的工具，但不能僅以分數作為評價的唯一標準，還需考慮學生在進行心理折疊時的認知過程．心理折疊雖與空間能力聯系密切，但有研究發現，初三至高一年級心理折疊能力發展迅速而空間能力發展變化不大[24]，說明心理折疊與空間能力的發展是非同步的，心理折疊有自身的發展規律．第二、三學段學生在認知上處于由具體運算階段向形式運算階段過渡的時期，正是空間能力形成和快速發展的時期．因此，這里對四~八年級學生的心理折疊認知過程進行探索．

3 設計與實施

3.1 測題編制

考慮到正方體是義務教育階段學生認識空間的基礎幾何體，測試題以正方體展開圖的折疊還原問題為工具，考察學生的心理折疊能力．結合心理折疊相關研究測試題設置[9]，以國外心理學相關測試網站[25]中的空間能力測試為基礎，設計不同認知負荷的心理折疊測試題．

表1 不同認知負荷測題具例

3.2 被試選取

采用便利抽樣，選取某縣城區兩所普通學校（一所小學與一所初中），在四~八年級每年級隨機選擇一平行班，依據數學學業成就高低，每班各選4人，共20名學生．將所在年級編碼為對應數字，學業成就由高至低編碼為A、B、C、D．如7A表示七年級學業成就最高的學生．

3.3 測試過程及數據收集

測試于2019年6月初完成．首先按年級分別對學生進行紙筆測試，測試時長為45分鐘．在測試過程中觀察學生做題時的行為（是否需借助外物幫助其進行折疊），并進行記錄．如低年級（四~五年級）部分被試出現動手轉動測題紙以幫助“轉動”展開圖，考慮心理折疊要求二維表象操作需在頭腦中進行，后續研究將涉及外物幫助完成任務的被試排除（4人）．

然后根據書面作答情況（特別是書面作答不夠詳細）選取學生進行訪談（11人），訪談主要問題為“你在做這道題時，是怎么思考的？”所選取的學校采用人教版數學教材，正方體展開圖于五年級下冊長方體和正方體一章中進行系統學習，在七年級下冊幾何圖形初步一章中進一步學習涉及面上圖案變化的展開圖．由于四年級被試沒有學習相關知識，五年級被試剛接觸展開圖，在解釋思路時出現無法作答或無法描述的情況，為詳細分析學生在心理折疊時的認知過程，采用目的性抽樣，考慮年級分布以及認知過程的獨特性和代表性，在訪談的六~八年級被試中選取5人（6D、6B、7D、8B、8C）作為進一步進行個案研究的對象．

4 結果與分析

主要以測題L、H為例（圖1、圖2），分析兩種認知負荷任務下學生的認知過程．

4.1 低認知負荷任務中學生的表現差異

比較低認知負荷任務中學生表現（見表2），除6D外，其余被試都得到了正確答案．被試6D在腦海中生成正方體困難，因此放棄作答；被試6B需先將展開圖還原為正方體后，再判斷選項是否正確；被試8C與6B相比，僅判斷選項涉及到的3面位置即可正確作答；而被試7D與8B則無需將展開圖還原為正方體，能迅速發現選項錯誤點準確判斷．在正確作答的4名被試中，6B完成任務需確定6面位置，8C需確定3面位置，而7D與8B則跳過了折疊過程無需確定各面位置直接得到判斷．從完全折疊正方體（折疊6面）到不完全折疊正方體（折疊3面），最后不需要進行折疊，被試關于面位置的圖式提取逐漸趨于自動化．

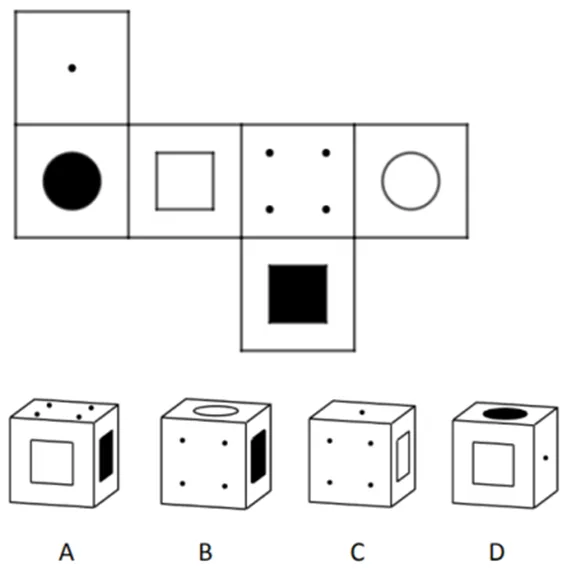
圖1 試題L（低認知負荷）

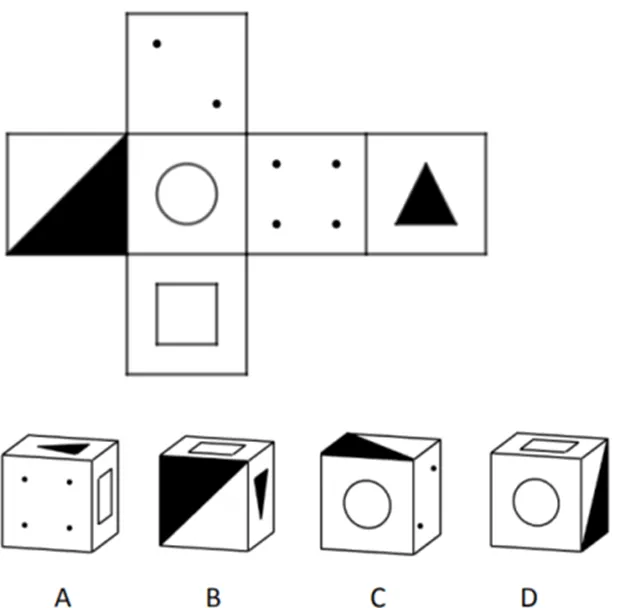
圖2 試題H（高認知負荷）

這一點在解決其它低認知負荷任務測題（圖3）時也有體現，需要折疊6面的6B仍需先判斷各面位置后再進行作答：“選C，有一個點的是在前面，這個正方形應該在上面，這個4點就在下面，這個黑色的正方形就在后面，5個點的在左面，它不在右邊．”需要折疊3面進行判斷的8C在訪談中提到：“因為那個選項只會給你顯示3個圖形，然后我先去找兩個，如果兩個比對上的話我就找第三個，如果第三個不對就百分之百不是那個選項．”被試7D與8B則同樣跳過了折疊過程，直接說明若按C選項擺放5點面不可能在右邊．4個被試都能準確判斷面的位置，但關于面位置的圖式提取存在差異：被試6B需完全確定面的位置，被試8C需確定選項所給面的位置，而被試7D與8B則能快速提取圖式直接判斷面位置的錯誤．可見，在低認知負荷任務中，相關圖式提取是否達到自動化是導致學生之間表現差異的主要原因．

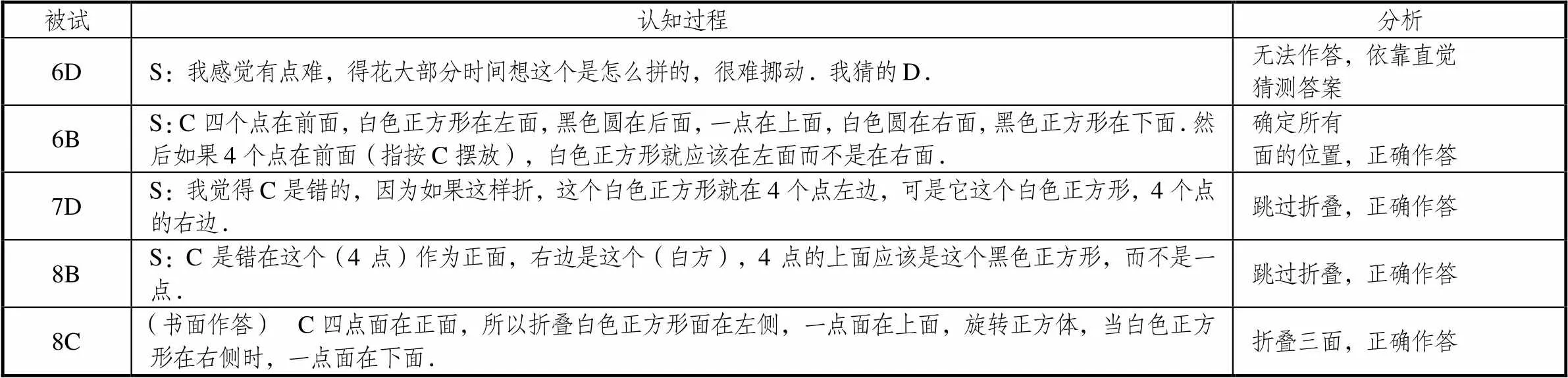
表2 被試解決低認知負荷任務（試題L）的認知過程

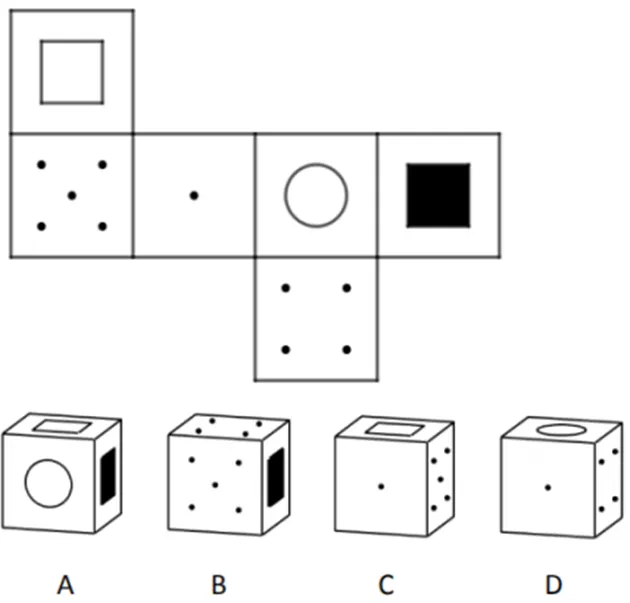
圖3 低認知負荷任務測題

4.2 高認知負荷任務中學生的表現差異

在高認知負荷任務中，學生的表現差異可能與相關圖式的建構有關．從表3中不難看出，被試6D仍停留在判斷面的位置這一階段，或許是因為該被試關于面位置的圖式未完成建構，從而無法進入認識圖案變化這一階段；被試6B不能將圖案變化與位置關系正確關聯，雖然該被試能意識到二維表象旋轉會帶動圖案發生變化，但其生成的三維空間圖形是錯誤的（直角三角形面旋轉后圖案變化錯誤）；被試7D則認為非中心對稱圖形（小三角形面）不會因旋轉而發生改變；被試8B與8C判斷各面位置后能正確認圖案變化．或許是因為需關聯其它要素（圖案變化）加大了認知負荷，被試6B與7D關于圖案變化的圖式可能未完成建構，導致6B判斷圖案錯誤，7D認為圖案不會改變；而被試8B與8C能正確說明圖案變化，說明被試8B與8C較被試6B與7D而言，建構的相關圖式更完全．

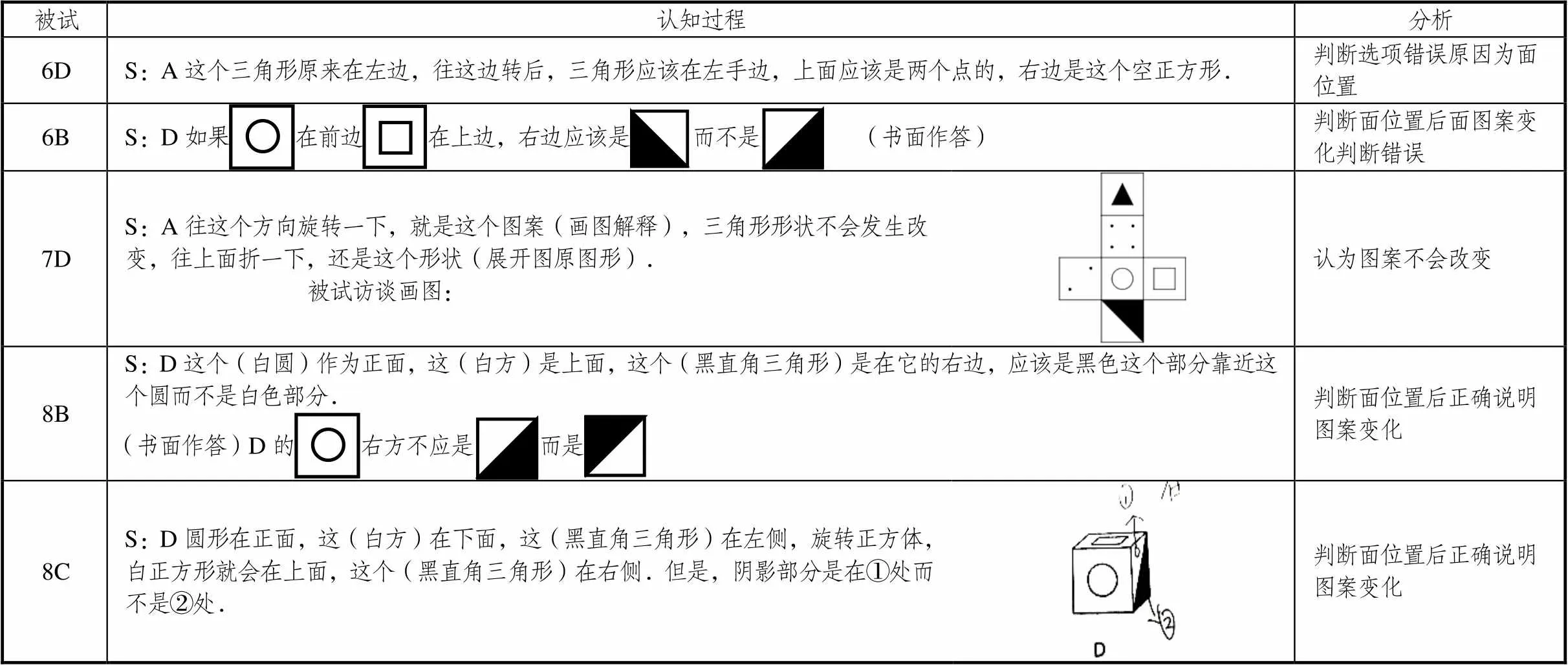
表3 被試解決高認知負荷任務（試題H）的認知過程

對比5名被試在不同認知負荷任務的認知過程（表2、表3）發現，在低認知負荷任務中正確作答為4人，高認知負荷任務正確作答2人，可見被試在低認知負荷任務表現更好；若無法成功完成低認知負荷任務，則通常不能在高認知負荷任務中表現良好（被試6D）；相關圖式建構可能是完成高認知負荷任務的基礎（被試8B與8C）．

4.3 學生心理折疊水平的劃分及認知特征界定

對不同認知負荷任務下學生認知過程的分析中不難發現，心理折疊可能存在水平層次．在心理折疊過程中，各面位置發生改變的同時會引起面上圖案發生變化，學生不僅需掌握各面位置關系和圖案變化這兩條信息量，還要將其關聯起來共同考慮．低認知負荷任務僅涉及各面位置關系，高認知負荷任務涉及各面位置與圖案變化的交互．結合學生不同認知負荷任務的完成情況，可將心理折疊分為3種水平（表4）．為增強被試水平判定可靠性，所有被試均由研究小組各成員獨立判定水平，若出現差異，則合議后確定．

表4 心理折疊水平劃分

為深入分析每一種心理折疊水平的特征表現，接下來對各被試在不同認知負荷任務中的認知特點進行具體分析．

4.3.1 水平1被試無法正確認識各面所在位置

從表5可以看出，處于水平1的被試6D是將展開圖各面進行“堆疊”，像“滾雪球”般對展開圖進行折疊．由6D的書面標記可看出，該被試將二維圖形看作內表面展開圖，可若為內表面展開圖，則這兩題答案不唯一，但6D僅選擇一選項，說明其并不具備對二維表象進行操作的能力．在低認知負荷任務中，被試6D解答出現邏輯錯亂，錯誤地將正方體的相連面認為是對立面，因此無法正確判斷各面位置；在高認知負荷任務中，被試6D認為是面位置錯誤，而該題實際錯誤為非中心對稱圖案在轉動過程中發生變化，由于該被試還不能正確判斷面位置，因此無法進一步關注圖案變化，說明思路時也沒有提到圖案對正方體的影響．這進一步證實了相關圖式建構是完成高認知負荷任務的基礎，由于6D不能正確認識各面位置，說明其關于面位置的圖式建構還未完全，導致6D在解決高認知負荷任務時仍停留在判斷面位置這一階段，無法考慮面上圖案的變化，這也是6D與其他被試在心理折疊表現上出現差異的根本原因．

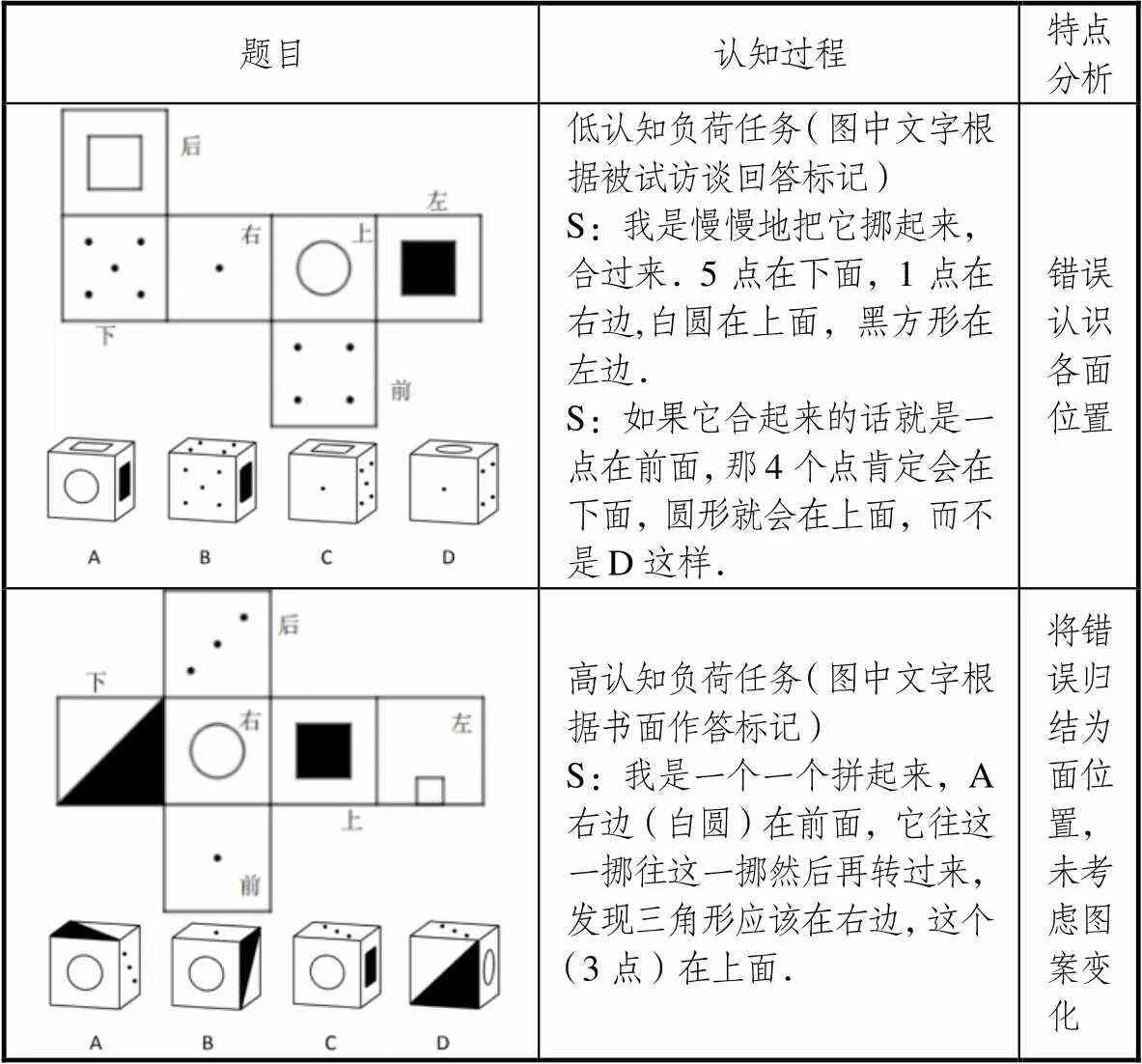
表5 被試6D的認知特點

4.3.2 水平2被試無法正確認識圖案變化

從表6不難發現，被試6B與7D在低認知負荷任務表現良好，都能正確認識各面所在位置，并說明選項錯誤原因：6B確定所有面的位置后正確判斷，7D則無需折疊直接得到正確解答；兩被試都無法正確完成高認知負荷任務：6B仍需先確認各面位置，當發現面的位置正確后該被試沒有判斷圖案變化，認為自己錯了就放棄作答，7D則沒有意識到兩點面會隨著折疊發生變化，所以沒有描述關于圖案運動后的正確變化，錯誤地認為選項正確．可見，被試6B與7D雖已能正確判斷各面位置，但當面上圖案涉及非中心對稱圖形時，他們無法認識到圖案的變化從而不能得到正確解答．因此，處于水平2的學生僅能處理折疊時各面位置這一條信息，無法將圖案變化與位置變化聯系起來回答問題．

比較被試6B在兩種認知負荷任務中的表現可發現，6B已能清楚地認識到各面所在位置關系，從而能正確地完成低認知負荷任務，說明其關于面位置的圖式建構已完成；當折疊任務涉及圖案變化時，結合表3中6B的表現可發現，被試6B還不能準確判斷由于折疊轉動引起的非中心對稱圖形是如何變化的，導致其無法完成高認知負荷任務，說明被試6B關于面上圖案變化的圖式還未完成建構．比較被試7D在兩種認知負荷任務中的表現亦可看出，其關于面位置的圖式已完成建構，能夠準確完成低認知負荷任務，結合表3中7D的表現可見，被試7D沒有認識到圖案會由于折疊轉動發生變化，因此無法完成高認知負荷任務．

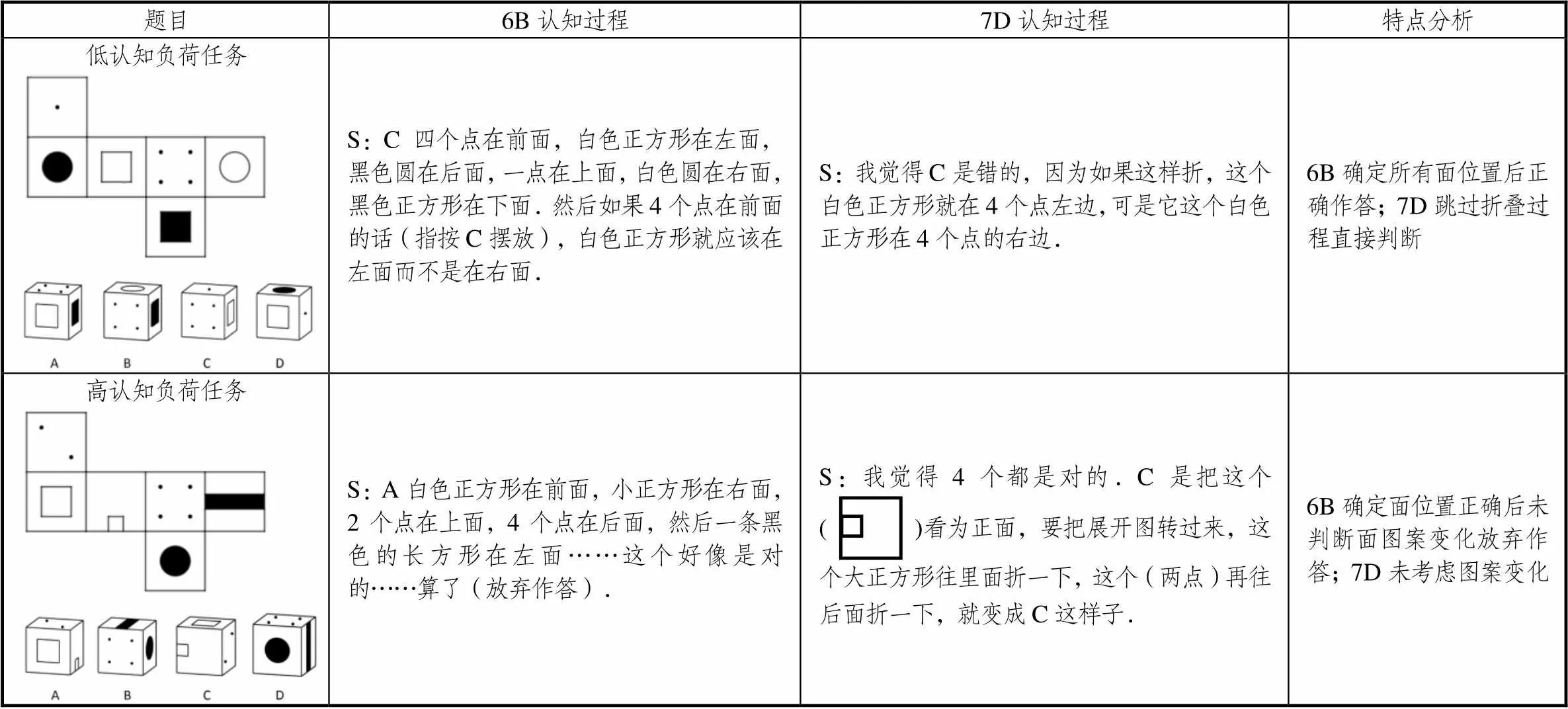
表6 被試6B與7D的認知特點

4.3.3 水平3被試能正確認識各面位置及圖案變化

由表7可知，被試8B與8C已能成功完成高低兩種認知負荷任務．在低認知負荷任務中，8C確定3面位置后再對表象進行旋轉操作得到正確判斷，8B關于面的位置關系這一條信息處理已達到自動化，即無需先確定各面所在位置再判斷選項是否符合要求，能直接得出正確結論和選項錯誤原因；在高認知負荷任務中，8B與8C都能夠在判斷各面位置關系正確的基礎上，關注直角三角形面圖案變化并能說出正確圖案．因此，處于水平3的學生能關注心理折疊所有要素及關系進行解答，確定各面位置關系的同時兼顧認識圖案在操作時發生的變化．

比較被試8B在兩種認知負荷任務中的表現，注意到8B關于面位置的圖式提取已達到自動化水平，但在解決高認知負荷任務時，8B未能自動提取該圖式，仍需先判斷面位置后再判斷圖案變化，這或許是因為在高認知負荷任務中，工作記憶需要處理面位置和圖案變化兩條信息量，加大了認知負荷，從而導致圖式自動提取失敗．可見被試8B關于圖案變化的圖式或未完全建構，因此在完成高認知負荷任務時不能直接判斷圖案變化，需經歷確定各面位置的過程來確定圖案是如何轉動的，由此判斷最終圖案．

基于對3種水平被試認知特點的分析，可以對心理折疊水平劃分及認知特征進行界定（見表8）．

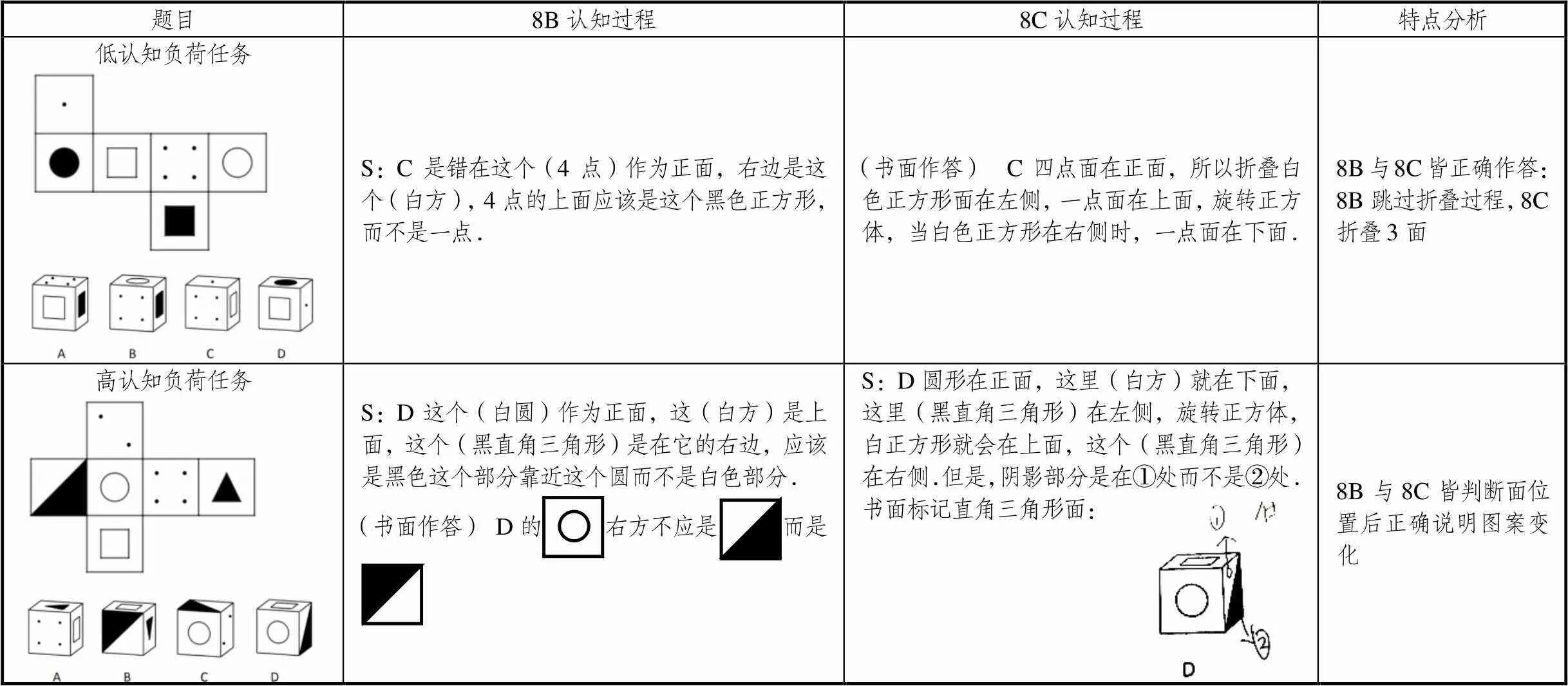
表7 被試8B與8C的認知特點

表8 心理折疊水平劃分及認知特征界定

5 結論與討論

研究發現學生的心理折疊表現中，低認知負荷任務優于高認知負荷任務；在低認知負荷任務中，學生的表現差異可能與圖式的自動化有關，而圖式建構或與高認知負荷任務的學生表現差異相聯系．辛自強指出：圖式的自動化和結構化可以有效降低認知負荷，是造成專家和新手問題解決技能差異的根本原因[26]，這或許可以解釋為什么圖式在心理折疊中亦發揮了降低認知負荷幫助學生解決問題的作用，具有更豐富圖式的學生能完成更高認知負荷的任務．

研究還發現學生心理折疊水平可以分為3種：（1）前操作水平；（2）單一操作水平；（3）關聯操作水平．研究對象的心理折疊水平隨年級增高而增加，七年級被試處于單一操作水平而八年級兩被試皆處于更高水平，這與周珍的研究結果[9]相似：初一至初二年級心理折疊快速發展．另外，黃興豐發現學生的空間幾何思維在各個水平上的發展可能是同時發生的，并非像范希爾所假定的那樣，一定要在前一個水平完全獲得的前提下，后一水平才能發展[27]．心理折疊水平作為空間能力的一部分，是否也同空間幾何思維水平一樣具有發展階段？各階段之間是否具有可跨越性？這些問題尚待今后繼續研究．

6 思考與建議

如前所述，圖式建構與自動化的差異可能是導致學生心理折疊表現差異的主要原因．也有研究已發現圖式數量和圖式自動化的水平是專家與新手在問題解決中的本質區別[16]．在數學教學中，教師常常需要讓學生在問題解決領域從新手變成專家[11]．如何讓學生在數學空間能力方面更快步入更高水平？研究結論啟示教師或許可以從幫助學生建構圖式與促進圖式自動化著手．另外，如果將數學知識看作數學學習的邏輯起點，那么學情則是展開數學學習的現實起點[28]．研究還發現了心理折疊水平可分為3個層次，教師可藉此了解學生的數學空間能力，從而在準確把握學生已有認知水平的基礎上，有針對性開展教學活動，發展學生的數學核心素養．

6.1 合理逐次增加學習難度幫助學生建構圖式

圖式獲得是數學知識理解的本質[29]，李士锜認為：“學習一個數學概念、原理、法則，如果在心理上能組織起適當的有效的認知結構，并使之成為個人內部知識網絡的一部分才說明是理解了．”[30]根據學生的學習水平，適當降低學習材料的復雜程度，可以幫助學生在問題解決的過程獲得相應圖式．如在正方體展開圖教學中，可設計有難度層次的題目，逐個增加展開圖具有不對稱圖案面的個數，讓學生在獲得涉及一個不對稱圖案如何進行折疊的圖式后學習多個不對稱圖案的折疊，能有效地幫助其建構相關圖式．

空間教學與其它知識教學不同之處在于培養空間感知可通過動手實踐，采用實物演示讓學生經歷二維表象到三維圖形的變換，可讓學生體會圖形從二維到三維的變與不變，為進行抽象和想象空間圖形時提供實際背景．在獲得基本感知后，要求學生逐漸脫離實物進入更高難度的思維鍛煉，也是幫助圖式建構的方法之一．

6.2 加強思維訓練促進學生提取圖式達到自動化

需要注意的是，實物的作用是幫助學生進行觀察、分析，僅依靠動手操作對空間概念形成沒有幫助，圖式無法在頭腦中建構．如四~五年級被試采用動手操作的方法僅能完成可由展開圖“轉動”解決的任務，無法回答需抽象思考的問題．在空間教學中鼓勵學生動手操作的同時要上升思維訓練的高度，尤其是對于高年級學生，過多依賴實物模型可能會阻礙抽象思維和空間能力的發展．

正如學生掌握九九乘法表后遇到乘法運算能產生條件反射快速得到答案，圖式提取不占用工作記憶空間．當提取趨向自動化，工作記憶就能有更大空間處理更高難度問題．在教學中利用變式“重復”練習[31]，可以有效促進圖式自動化．譬如，可對空間概念進行變式訓練，讓學生理解正方體的對立面與相鄰面在二維展開圖中位置關系是如何表示的，發現二維圖形在平面上的旋轉與空間中旋轉的共通之處．在此基礎上，適當增加練習量讓學生多次經歷圖式提取過程，在量的積累上達到自動化水平．

6.3 利用心理折疊水平合理評價學生數學空間能力

發展數學核心素養要改變評價方式單純依賴一張試卷的狀況[32]．分數是對學生學習的結果性評價，教師在進行教學評價時應更加關注過程性評價．如何整合評價與客觀測驗形成“測驗嵌入式”評價，如何切合數學教學實際形成系統化的“教學嵌入式”評價都亟待實踐研究[33]．心理折疊水平就是動態觀察學生數學空間能力的一個有效工具，在教學中判斷學生心理折疊達到何種水平，就能發現學生在空間學習過程中遇到的具體困難是什么，從而有針對性地開展教學，真正做到因材施教[34-42]．譬如，若判斷學生處于前操作水平，則可以在教學中多采用實物模型，先讓學生建立空間感知，在此基礎上進行下一步學習．在每一個具體的水平層次上，開展能夠促進該水平層次的學生提高的教學，以學生已有的認知水平為基礎引導其向更高水平前進，才能有效地幫助學生獲得進一步提升．

[1] 施建農，周林，查子秀，等．兒童心理折疊能力的發展[J]．心理學報，1997，29（2）：160–165．

[2] MILIVOJEVIC B, JOHNSON B W, HAMM J P, et al. Non-identical neural mechanisms for two types of mental transformation: Event-related potentials during mental rotation and mental paper folding [J]. Neuropsychologia, 2003, 41 (10): 1?345–1?356.

[3] 周珍，周江霞，張景斌，等．不同認知方式中學生空間圖形認知能力發展與數學成績關系研究[J]．數學教育學報，2013，22（5）：62–65．

[4] LEAN G, MA-KEN C. Spatial ability, visual imagery, and mathematical performance [J]. Educational Studies in Mathematics, 1981, 12 (3): 267–299.

[5] 中華人民共和國教育部．義務教育數學課程標準（2011年版）[M]．北京：北京師范大學出版社，2012：5．

[6] 中華人民共和國教育部．普通高中數學課程標準（2017年版）[M]．北京：人民教育出版社，2017：6．

[7] 吳宏，汪仲文．中小學生空間能力的構成要素與水平層次及評價指標[J]．數學教育學報，2014，23（5）：41–45．

[8] 周珍．中學生心理展開能力與心理折疊能力發展的對比研究[J]．數學教育學報，2010，19（1）：30–32．

[9] 周珍，連四清，周春荔．中學生空間圖形認知能力的發展研究[J]．數學教育學報，2001，10（1）：75–78．

[10] 周珍，周江霞，張景斌，等．中學生認知方式對心理折疊能力發展的影響研究[J]．數學教育學報，2012，21（3）：35–37．

[11] 龐維國．認知負荷理論及其教學涵義[J]．當代教育科學，2011（12）：23–28．

[12] 陳巧芬．認知負荷理論及其發展[J]．現代教育技術，2007，17（9）：15–16，19．

[13] ?COOPER G. Cognitive load theory as an aid for instructional design [J]. Australian Journal of Educational Technology, 1990, 6 (1): 108–113.

[14] 張慧，張凡．認知負荷理論綜述[J]．教育研究與實驗，1999（4）：45–47．

[15] 陳琦，劉儒德．教育心理學[M]．2版．北京：高等教育出版社，2011：145．

[16] 楊心德，王小康．認知心理學視野中的認知負荷理論[J]．寧波大學學報（教育科學版），2007，29（3）：11–15．

[17] 張睆，辛自強．基于認知負荷理論的數學學優生教學[J]．教育學報，2010，6（3）：59–65．

[18] ?HARRIS J, HIRSH-PASEK K, NORA-S N. Understanding spatial transformations: Similarities and differences between mental rotation and mental folding [J]. Cognitive Processing, 2013, 14 (2): 105–115.

[19] 楊孟萍，石德澄．空間認知能力的測驗研究[J]．心理發展與教育，1990（4）：213–217．

[20] 徐凡，施建農．四~五年級學生的空間表征與幾何能力的相關性研究[J]．心理學報，1992，24（1）：20–27．

[21] 周珍，連四清，周春荔．中學生空間圖形認知能力發展的性別差異研究[J]．數學教育學報，2001，10（4）：93–95．

[22] 周珍，連四清，周春荔．中學生空間圖形認知能力發展與數學成績關系及其與智力的相關性研究[J]．數學教育學報，2005，14（1）：57–58，94．

[23] 周珍，周江霞，張景斌，等．不同認知方式中學生的空間圖形認知能力發展研究[J]．數學教育學報，2012，21（6）：38–42．

[24] 周珍．中學生空間圖形認知能力發展的研究[D]．北京：首都師范大學，2000：10，17．

[25] 123test.com. Spatial reasoning test 123test.com [EB/OL]. (2019–12–12) [2019–03–30]. https://www.123test.com/ spatial-reasoning-test/.

[26] 辛自強，林崇德．認知負荷與認知技能和圖式獲得的關系及其教學意義[J]．華東師范大學學報（教育科學版），2002，20（4）：55–60，77．

[27] 黃興豐，裔晶晶，孫慶慶，等．高三學生空間幾何思維水平發展的調查研究[J]．數學教育學報，2016，25（2）：75–79．

[28] 沈海玲，黃龍玲．瞄準數學素養精準教學設計[J]．小學數學教育，2019（Z3）：40–41．

[29] 黃燕玲，喻平．對數學理解的再認識[J]．數學教育學報，2002，11（3）：40–43．

[30] 李士锜．PME：數學教育心理[M]．上海：華東師范大學出版社，2001：64–87．

[31] 張奠宙，宋乃慶．數學教育概論[M]．2版．北京：高等教育出版社，2009：67．

[32] 史寧中，林玉慈，陶劍，等．關于高中數學教育中的數學核心素養——史寧中教授訪談之七[J]．課程·教材·教法，2017，37（4）：8–14．

[33] 謝圣英，沈文選．透視數學表現性評價[J]．數學教育學報，2006，15（1）：22–24，98．

[34] 俞宏毓，朱向陽，顧泠沅．管窺小學數學課堂教學現狀——“兩位數減兩位數退位減法”教學案例分析[J]．數學教育學報，2019，28（1）：43-48．

[35] 李欣蓮，宋乃慶，陳婷，等．小學數學教師“問題提出”表現研究[J]．數學教育學報，2019，28（2）：1-6．

[36] 陳婷，徐紅，徐冉冉，等．數學教師學習使用“問題提出”教學法的個案研究——以“用字母表示稍復雜的數量關系”為例[J]．數學教育學報，2019，28（2）：7-12．

[37] 張輝蓉，冉彥桃，劉蝶，等．教師“問題提出”教學知識建構[J]．數學教育學報，2019，28（2）：13-17．

[38] 許天來，蔡金法．美國數學課程中的“問題提出”——期望與挑戰[J]．數學教育學報，2019，28（2）：18-23．

[39] 王紅權，李馨．從系統的觀點看一元二次方程的解法教學設計[J]．數學教育學報，2019，28（3）：94-97．

[40] 程明喜．小學數學“深度學習”教學策略研究[J]．數學教育學報，2019，28（4）：66-70．

[41] 李懷軍，張維忠．小學生數學問題提出能力發展研究[J]．數學教育學報，2019，28（5）：2-8．

[42] 楊紅萍，楊捷．小學生數學閱讀能力結構的因素分析[J]．數學教育學報，2019，28（5）：14-18．

Research on Students’ Mental Folding Levels Based on Tasks with Different Cognitive Demand

ZHONG Yi, XIE Sheng-ying

(School of Mathematics and Statistics, LHPCSIP (MOE), Hunan Normal University, Hunan Changsha 410081, China)

Cultivating students’ ability for spatial visualization is an important goal in mathematics education. Mental folding is one of the important manifestations of spatial visualization. Studies of the cognitive process of students’ mental folding on tasks with different levels of cognitive demand have found that students perform better on low cognitive-demand tasks than on high cognitive-demand tasks. High student performance on low cognitive-demand tasks is related to schema automation, whereas high student performance on high cognitive-demand tasks is related to schema construction. The level of mental folding can be classified into the following categories: pre-operational level, single-operation level, and complex-operation level. Research on determining students’ mental-folding levels can help us to improve students’ mathematical spatial visualization so that we can carry out targeted teaching based on our understanding of students’ existing cognitive level to develop students’ mathematical core competency.

mental folding; cognitive load; spatial ability; mathematical thinking

G442

A

1004–9894（2020）03–0025–07

2020–01–19

湖南省教育廳一般項目——湖南高考自主命題數學試題研究——基于SOLO分類理論（15C0873）；湖南省重點學科建設項目

鐘熠（1996—），女，貴州三穗人，碩士，主要從事數學課程與教學論研究．謝圣英為本文通訊作者．

鐘熠，謝圣英．基于不同認知負荷任務的學生心理折疊水平研究[J]．數學教育學報，2020，29（3）：25-31．

[責任編校：周學智、陳漢君]