樹立應用意識　提高學生素養

摘 要：以行程問題為背景的一次函數與一元一次方程綜合應用題是近年中考中常見的題型.教師要重視基礎，引導學生探尋通性通法，提煉解題模型，挖掘蘊含的數學思想.在提升學生解題能力的同時，訓練學生的思維，樹立學生的應用意識，從而提高學生的素養.

關鍵詞：解題能力;數學思想;應用意識;學生素養

作者簡介：羅強華（1984-），男，四川營山人，本科，中學一級教師，研究方向：中學數學教學與解題.

1 試題呈現

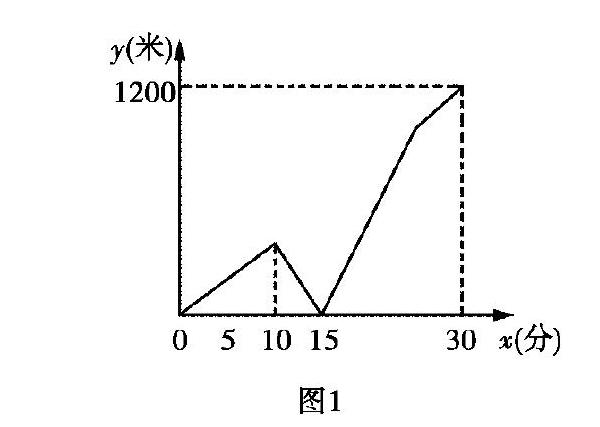
題目 （2018年重慶B卷第17題）一天早晨， 小玲從家出發勻速步行到學校.小玲出發一段時間后，她的媽媽發現小玲忘帶了一件必需的學習用品，于是立即下樓騎自行車，沿小玲行進的路線，勻速去追小玲.媽媽追上小玲將學習用品交給小玲后，立即沿原路線勻速返回家里，但由于路上行人漸多，媽媽返回時騎車的速度只是原來速度的一半.小玲繼續以原速度步行前往學校.媽媽與小玲之間的距離y（米）與小玲從家出發后步行的時間x（分）之間的關系如圖1所示（小玲和媽媽上、下樓以及媽媽交學習用品給小玲耽擱的時間忽略不計）.當媽媽剛回到家時，小玲離學校的距離為米.

2 特色解讀

2.1 貼近生活，體現應用功能

本題的背景是學生熟悉的生活情境，甚至是一些學生的親身經歷，讓學生感到親切而輕松，可以緩解考試中的緊張情緒，彰顯了以學生為本的理念.題目貼近實際生活，讓學生感受到數學來源于生活，又服務于生活，培養學生的應用意識和解決實際問題的能力，讓學生明白學習數學的用處，體現了數學的應用功能.此外，題目的背景也展現了一個母親對孩子的關愛和無私的付出，讓學生在緊張的考試中還能體會到強大的母愛，體現了數學學科的育人功能，哪怕是中考也不忘對學生進行情感教育.

2.2 基于平常，給予正確導向

本題是一次函數與一元一次方程的綜合應用題，涉及到一次函數圖象的性質、行程問題中的追及問題和關系式“路程=速度×時間”等知識.重慶近幾年的中考數學試卷中都出現了此類題目.題目雖有難度，但不是那種偏、難、繁、怪題，并非高不可攀.題目中涉及的基礎知識、基本技能、基本思想和方法都是教師平常經常強調的重點，是學生所熟悉的內容.看到熟悉的題型，給考生帶來希望，不至于望而卻步，直接放棄.只要學生在平常認真練習、思考和體會，在考試時通過耐心細致地分析和解答，還是能夠做出來的.但是又不能憑運氣胡亂猜出答案.這對以后學生的學習和教師的工作都給予正確的導向，讓學生明白在平時要踏實、勤奮和努力地學習，不能臨陣磨槍，更不能投機取巧;也讓教師清楚了今后教育教學工作中的重點，知道了如何更有效和有針對性地教育和引導學生.

2.3 數形結合，蘊含數學思想

數形結合是一種重要的數學思想.華羅庚曾說：“數缺形時少直觀，形少數時難入微.數形結合百般好，隔離分家萬事休.”在數學中，數和形是兩個主要的研究對象，它們之間有著密切的聯系.在一定條件下，數和形之間可以相互轉化、互相關聯.本題很好地應用和體現了數形結合思想，并將其與方程思想和函數思想相結合，展現出強大的邏輯思維和數學思想.

（1）題目中，媽媽與小玲之間的距離y（米）與小玲從家出發后步行的時間x（分）之間的關系通過函數圖象表示出來.函數圖象和題目條件中的數量相互結合，緊密聯系在一起，互為補充.一些能力強的學生將函數圖象和題目條件結合起來，就能領會題意，找到解決問題的方法，得出答案.

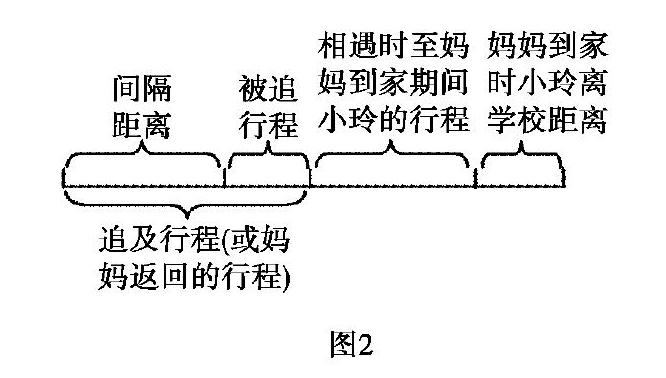
（2）對于一些理解力或想象力較弱的學生還可以根據題意畫出線段圖，利用幾何直觀來理解題意，解決問題.本題可以畫出如圖2所示的線段圖.通過數形結合審題可知，家到學校的距離為1200米，小玲30分鐘走完，

可以求出小玲的速度為40米/分.小玲離家10分鐘時，媽媽去追她，5分鐘后，媽媽追上小玲，可以求出媽媽追及的速度為120米/分和返回時的速度為60米/分.由此可求出媽媽返回的時間為10分鐘，此時，小玲已經走了25分鐘，還剩下5分鐘的路程，從而求出小玲離學校的距離為200米.

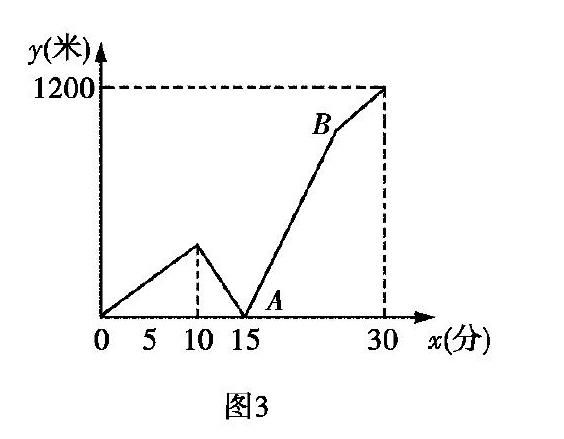
（3）在解題時，除了用一元一次方程的方法求解之外，還可以借助函數圖象求出函數關系式，用解析法求解.根據題意可以求出圖3中直線AB的函數解析式為：

y=100x-1500.當媽媽到家時，x=25，可求出y的值為1000，即小玲離家的距離為1000米，離學校的距離為200米.

2.4 運用模型，突出通性通法

縱觀重慶近幾年的中考數學試卷，此類題目不外乎是一次函數與相遇問題或追及問題的綜合應用.考查的是平常所學習的核心知識和基本模型，突出了通性通法.

例如，本題涉及了追及問題，其線段圖如圖4所示，關系式為：“追者的行程-被追者的行程=間隔的距離”或“（追者速度-被追者速度）×追及時間=間隔的距離”.

有時也涉及到相遇問題，其線段圖如圖5所示，關系式為：

“甲的行程+乙的行程=總路程”或“（甲的速度+乙的速度）×相遇時間=總路程”.

解決此類問題的基本思路是：首先結合函數圖象和線段圖審懂題意，特別是函數圖象中的自變量、因變量和每個交點所表示的實際意義，這是解決問題的前提;然后根據題意并運用模型求出相關人員的速度，這是解決問題的關鍵;最后求出答案.

3 教學導向分析

3.1 重視基礎，提升解題能力

《義務教育數學課程標準（2011年版）》明確提出：通過義務教育階段的數學學習，學生能獲得適應生活和進一步發展所必須的數學基礎知識、基本技能、基本思想和基本活動經驗[1].即我們現在常說的“四基”.這是學生應用數學解決問題的重要而強大的支撐.教師在平常教學中，要重視基礎知識教學，要求學生理解并掌握概念、公式和性質等;加強訓練學生的基本技能，特別是分析能力、理解能力、推理能力、運算能力和應用能力等;不斷向學生滲透數學思想和方法.