“小數的初步認識”教學中十進分數的介入方式

趙勝華 徐軍紅

【摘? ?要】基于思維可視化教學理念，“小數的初步認識”的教學，可以通過激活十進分數以“符號操作”的方式介入小數意義建構，使小數的“十分”與“十進”的動態過程在頭腦中可視化，從而使學生的思維從靜態走向動態、從復雜走向簡潔，立體建構小數的意義。

【關鍵詞】小數;思維可視;教學

思維可視化教學是指通過一定的教學策略，幫助學生理解知識的產生和形成過程，使思維變得“看得見”、可琢磨。基于思維可視化教學理念，我們重構教學如下。

一、畫圖表征，具象解惑

學生是帶著自己對小數的了解來到課堂的，且各有差異。實踐中我們采用了特級教師袁曉萍設計的材料，在操作上做了新嘗試。

【教學片段1】

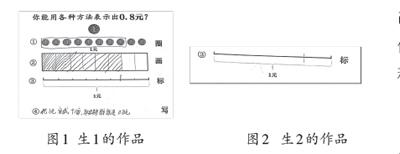
師：你能選擇合適的圖形來表示你對0.8元的理解嗎？

教師提供學習單，學生獨立嘗試解決，小組交流。之后全班討論，逐一呈現錯例，學生說明想法，再糾正完善。

生：我不同意生1的想法（如圖1），他只畫了6格，不能表示0.8元。

生：要平均分成十等份，再取其中的8份，他分錯了。

生：我心里想的是十等份，畫錯了。

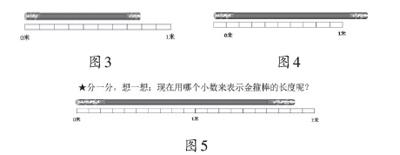
師：感謝你的失誤帶給我們思考。我們再來看生2的創作（如圖2）。你來猜猜看，他是不是很任性地點上了這一點？

生：不是的，他這里有看不見的十等分。

生：還有看不見的8等分和2等分。

（師生合作完善等分方法）

師：為什么十等分呢？

生：1元里有10個1角，把1元平均分成10份，每一份是1角，也就是0.1元，8份是8角，也就是0.8元。

（引導學生規范語言表征：把1元平均分成10份，取8份，就是0.8元）

【設計意圖】

1.小數的產生源于計量的需要。張奠宙先生認為，小數的出現是基于十進制表示數量的需要。史寧中先生認為建立小數的概念，一方面是為了現實世界中數量表達的需要;另一方面是為了數學本身的需要，主要是為了表示無理數，即小數的范圍要比分數的范圍廣。

有限小數是一種特殊的分數（十進分數），理解小數的核心在于重新理解十進制，即理解“十分”與“十進”。教學中要引導學生初步感受到：小數并不是十進分數改寫產生的，而是特殊平均分（十分）的結果，是自然數的十進位置值從高位往低位擴展的結果。

2.畫圖表征使經驗可視化。畫圖表征能幫助學生在客觀問題與主觀心智表達之間建立起一座橋梁，能充分暴露學生的已有經驗，使學生經驗可視。學生在“畫圖—讀圖—用圖”的過程中，明白自己已經知道了什么，還存在怎樣的困惑，并借助錯例糾正歸納共同點，“逼”學生將10的冪次方等分和合的過程“說清楚”，將內隱的思維可視化。

二、符號表征，改造經驗

借助一定的視覺表征形式，可使抽象的概念具象化，有利于學生獲得對知識本質的直觀、簡潔、清晰的理解。但不可忽視的是，表征之間的轉化是學習的關鍵環節，轉換能力不佳會影響數學學習。激活十進分數的“過程”可實現圖和文之間的心理轉換。

【教學片段2】

師：（逐一展示正例）這些表示方法有什么共同點？

生：都是十等分取8份。

師：如果用一個分數表示這些圖的共同特點，你會用哪個分數？

生：[810]。

師：從[810]你看到怎樣的分和取？

生：都是把1元十等分，取8份。

師：8角和0.8元之間用哪個數學符號來連接？（等號）那[810]應該放在哪個位置呢？8角和0.8元都帶有一個單位，想一想，[810]帶上怎樣一個單位比較合適？

生：我認為應該和0.8元在一起，因為都是先把1元平均分成10份，再取了8份。

生：[810]是把1元看作單位的，應帶上的單位是“元”。

生：這三個數的大小是一樣的。

在互動中，移動紙卡片，建立等式 8角=[810]元=0.8元。

師：[310]元，你想到什么？

【設計意圖】

1.英國沃瑞克大學的韜爾提出：數概念是一個典型的過程性概念，既是過程又是概念。學生建構數概念需要在具體操作的基礎上，通過壓縮和內化，逐步形成為對象的概念，并納入已有的認知結構。

分數概念和小數概念的建構都依據這樣的步驟展開，但兩者在建構過程中又有所區別，如分數初步認識時，學生鮮明感受的是“過程”，而小數初步認識時，由于已有的生活學習經驗，學生鮮明感受的反而是“對象”。因此，如何將兩者合理聯合是小數意義建構的關鍵。

2.十進分數以“符號操作”介入意義建構。像人民幣、面積模型、米制系統、數軸等直觀、半直觀模型的核心是“十分、十進”，從具體操作壓縮內化到對象，需要載體。誰能成為多功能載體呢？根據布魯納“三種操作”的認知理論，表象操作是實物操作到符號操作的橋梁，而十進分數這一富有“過程性”的數學語言恰能成為從符號操作到思維操作的橋梁。

教師以“如果用一個分數表示這位同學的想法，你會用哪個分數”引導學生用十進分數抽象過程，從而使分與合的動態過程可視化。然后以“[810]應該放在哪個位置呢”為驅動，借助紙卡片的移動自然地建構“8角=[810]元=0.8元”，既使學生感受到三者的相等關系，更使學生的思維從靜態走向動態，最后逆向思考“[310]元，你想到什么”。在互譯中，借助“數”（shǔ），初步體驗“十分”“十進”的思維過程。十進分數與小數的關系不僅限于對應關系，我們更應把它作為數學語言，成為學生思維和交流的載體。

三、動態表征，形成系統

當學生初步完成某一概念的建構后，教師可以在動態變化的情境中讓學生用所學的概念進行判斷，完善概念的建構。

【教學片段3】

師：孫悟空的金箍棒很神奇。你能根據下圖，用小數表示金箍棒每次變化后的長度嗎？

（1）學生根據金箍棒長短變化，口答小數（0.2米，0.8米，0.1米）。（圖3）

（2）（金箍棒快速伸長，產生新情況）你知道現在是幾米？（估：1～2米之間，接近1米）;顯示5等分，引發學生對1.1米與1.2米的爭論（隱藏的十等分）;繼續數1.4米，1.6米……2米。（圖4）

（3）（新沖突：1.82米）想用一個數準確表示現在金箍棒的長度，你會嗎？（圖5）

（4）課堂總結，梳理溝通。

【設計意圖】

什么樣的材料能實現米制系統的抽象過渡呢？“金箍棒”無疑是一個“有趣”的好材料。“金箍棒”在變長變短的動態表征中凸顯小數的“十分”，巧妙、無痕地發展了學生的數感，認識比1大的多位小數。

通過追問引導學生回顧學習歷程，從源頭再認識小數的意義，幫助學生將新概念納入自己的知識結構。

基于思維可視，激活十進分數以“符號操作”的方式介入小數意義建構，即借助十進分數這一數學語言，使小數的“十分”與“十進”的動態過程在頭腦中可視化，從而使學生的思維從靜態走向動態、從復雜走向簡潔，立體建構小數的意義。

參考文獻：

[1] 袁曉萍.學會向學生借智慧[M].杭州：浙江教育出版社，2018（11）：244-256.

[2] 史寧中.基本概念與運算法則[M].北京：高等教育出版社，2016（1）：16-19.

[3] 張奠宙.小學數學研究[M]. 北京：高等教育出版社，2009（1）：89-94.

[4] 鮑建生.數學學習的心理基礎與過程[M]. 上海：上海教育出版社，2014（4）：236-239.

[5] 蔣碧云.基于“數學理解層次”的教學路徑探索——思維可視化的另一種打開方式[J].上海教育科研，2019（22）：68-71.

（浙江省杭州市富陽區永興小學? ?311400

浙江省杭州市富陽區湖源鄉中心小學? ?311400）